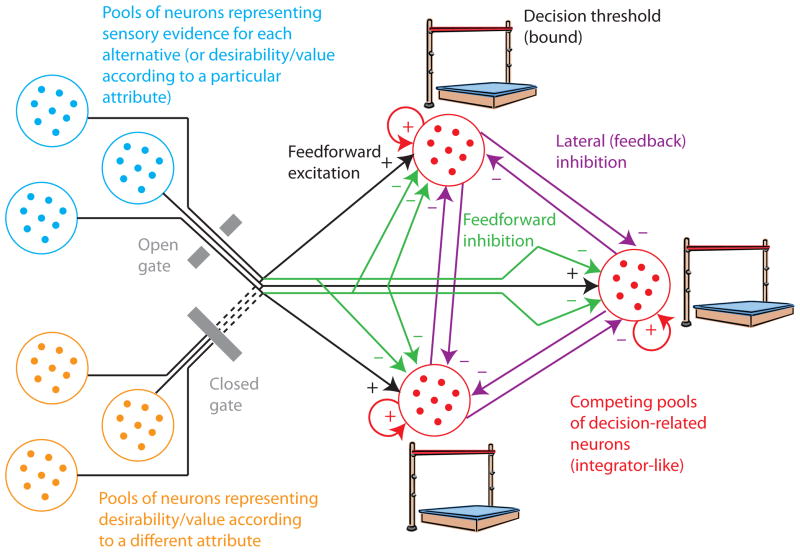
Figure 1. Structure of multi-alternative decision mechanisms.

Using an example of a decision between three alternatives, the structure of the majority of decision models is illustrated. The decision is based on a competition between three pools of decision-related neurons, one for each alternative (red). These pools of neurons exhibit integrator-like behavior, symbolized as recurrent excitatory feedback. Different models make different assumptions about the integration time constant (leakiness), the existence of a lower reflecting bound, and how the integrator is implemented (attractor dynamics). The simplest decision rule, which has been adopted by most of the models and is consistent with recordings from monkey LIP, is to terminate the decision process when the activity of the most active pool exceeds a decision threshold or bound (represented by high jump bar). More complicated decision rules, like a comparison between the most active and the second-most active pools, are possible. The blue pools of neurons provide sensory evidence for each alternative (in the case of perceptual decision-making) or the desirability or value of each alternative according to a particular attribute (in the case of economic or value-based decision-making). Multiple such representations might exist in the case of multi-attribute decision-making (orange pools). The proposed models for multi-attribute decision-making assume that only a single attribute can influence the decision at any time (open gate) and that the decision mechanism switches randomly between attributes over time. In all of the models, these evidence signals provide feedforward excitation to the decision pools (black arrows). The green arrows indicate feedforward inhibition, meaning that a particular evidence signal cannot only excite one decision pool, but also inhibit other decision pools. These connections are essential in diffusion-like models, present in MDFT, but absent in the standard version of LCA. Recent recordings from monkey LIP [18] suggest that they are present. The purple arrows indicate lateral or feedback inhibition, meaning that the decision pools directly compete with each other by suppressing each other’s activity. Such connections are absent in diffusion-like models, but essential for MDFT and LCA. In the case of MDFT the strength of these inhibitory connections depends on the similarity of choice options, in the case of LCA all inhibitory connections have the same strength. The depicted structure is highly simplified. For example, no interneurons for mediating inhibitory connections are shown.