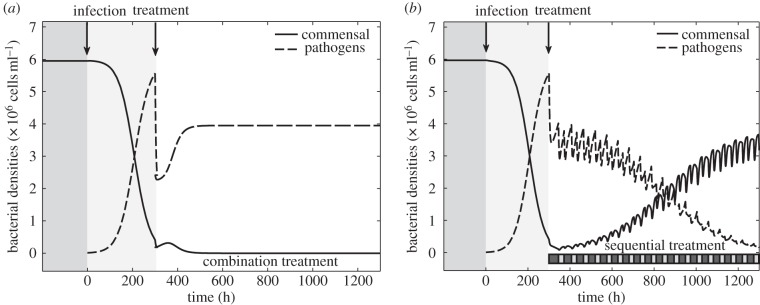
Figure 8.

Numerical simulations of a long-term experiment (T = 1300) of a complete competitive advantage scenario where the numerical values of the parameters used are given in table 1. In both examples, commensals are at equilibrium before susceptible pathogens are introduced into the system (at t = 0). The period when commensals (solid lines) are in equilibrium and there are no pathogens (dashed lines) present has a dark-grey background and the interval of time between initiation of infection and antibiotic deployment (at t = 300) has a light-grey background. The dashed line represents the sum over all pathogenic phenotypes while the solid line represents the density of commensals through the duration of the experiment. (a) All combination treatments select for drug-resistant pathogens, the initial benefit of treatment soon vanishes and pathogens colonize the system, driving the commensal to extinction. (b) In this example, commensals are able to persist with a sequential protocol designed using a feedback control heuristic. (The sequential protocol is illustrated with dark boxes denoting drug B and light boxes denoting drug A at the bottom of the figure.)