Linking community and disease ecology: the impact of biodiversity on pathogen transmission

Abstract

The increasing number of zoonotic diseases spilling over from a range of wild animal species represents a particular concern for public health, especially in light of the current dramatic trend of biodiversity loss. To understand the ecology of these multi-host pathogens and their response to environmental degradation and species extinctions, it is necessary to develop a theoretical framework that takes into account realistic community assemblages. Here, we present a multi-host species epidemiological model that includes empirically determined patterns of diversity and composition derived from community ecology studies. We use this framework to study the interaction between wildlife diversity and directly transmitted pathogen dynamics. First, we demonstrate that variability in community composition does not affect significantly the intensity of pathogen transmission. We also show that the consequences of community diversity can differentially impact the prevalence of pathogens and the number of infectious individuals. Finally, we show that ecological interactions among host species have a weaker influence on pathogen circulation than inter-species transmission rates. We conclude that integration of a community perspective to study wildlife pathogens is crucial, especially in the context of understanding and predicting infectious disease emergence events.

1. Introduction

For more than a century, there has been an exciting and mutually beneficial interplay between epidemiological theory and empirical research [1,2]. This has led to a deep understanding of host–pathogen interactions and the impact of a wide range of complexities that determine and affect transmission dynamics and host ecology. Much of this progress has been achieved, however, for systems with a substantially simplified ecology, with perhaps a disproportionately large focus on infectious diseases of humans and livestock [2–4]. The recent rise of zoonotic emerging infectious diseases [5–7] has increased our awareness of the ecological context of infectious diseases and has highlighted the chasm between standard theory and biological reality. We argue that what is called for is greater ecological sophistication in our epidemiological theory if we aim to explain zoonoses [8], identify the determinants of pathogen spillover [9–11] and understand the reciprocal impacts of infectious diseases and biodiversity [12–18].

The disconnect between current theory and empirical observations may be illustrated simply for directly transmitted pathogens. Dobson [19] explored host–pathogen community assemblages assuming density-dependent transmission (whereby an increase in host abundance results in an increase in the transmission rate owing to increased contact [2,20]). The consequences on transmission of introducing a novel species to the host community was found to depend not only on its relative susceptibility, but also on the competitive interactions in the host assemblage [21]. Assuming a simplified host community, with host abundances derived from allometric laws, Dobson [19] confirmed mathematically that transmission is amplified whenever the introduced species is assumed to increase overall host density or if it replaces a less susceptible species [21]. By contrast, empirical studies on rodent-borne diseases [22–24], assumed to be spread through density-dependent transmission, suggest that increased host species richness is associated with lower pathogen prevalence. The proposed explanation centres on ‘encounter reduction’, i.e. a decrease in contacts with the most susceptible species because of newly introduced hosts [10], and suggests that ecological interactions are a main component of pathogen transmission.

Here, in a bid to better link community ecology [25] and disease ecology [26,27], we propose a novel theoretical framework. It is composed of multiple host species, where species abundances are derived from empirical abundance relationships. We examine this model in the context of diseases with density-dependent transmission in order to assess how host community composition and diversity affect pathogen circulation. Overall, we demonstrate that variability in community composition, i.e. susceptibility of host species, does not qualitatively affect pathogen transmission. An increase in host species richness, however, can yield a greater number of infectious individuals, while simultaneously reducing their frequency in the whole host community (in other words, their prevalence). We discuss the implications of these results, especially in the context of rodent-borne diseases where the observation of reduced, or diluted, infection prevalence can—we submit—be a misinterpretation of empirical data. We conclude that considering a community perspective may give critical insights into epidemiological patterns reported for wildlife infections and may help to anticipate their dynamics.

2. Material and methods

We assume that pathogen dynamics is described by a classical Susceptible, Infectious and Recovered (SIR) model [2,4,26], which takes into account the possibility of multiple host species:

2.1

2.2

2.3

Each of the n host species is denoted by subscript i. The abundance of host species, N_i, is divided into three groups according to their infection status. At a per capita rate, b_i, immunologically naive individuals are born into the Susceptible class (S_i). Upon transmission, they become Infectious (I_i) and may subsequently transmit the pathogen to con- and hetero-specifics. At rate , infecteds move to the Recovered class (R_i), and are assumed immune for life. Finally, individuals are assumed to die at a constant rate, d_i, irrespective of their infection status.

The per capita transmission hazard is determined by the ‘force of infection’, λ_i. We assume here density-dependent transmission, thought to be appropriate for directly transmitted pathogens among wildlife [4,28] or humans [2], leading to:

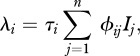2.4

where n represents host species richness, τ_i the susceptibility of species i (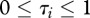), 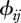the contact rate between species j and species i and I_j the number of infectious individuals from species j.

(a). Integrating ecological realism

We assume that host species comprise a community of vertebrate animals. To study realistic host community configurations, we quantify species ecology, i.e. their susceptibilities (τ_i), abundances (N_i), demographic rates (b_i and d_i) and heterospecific contact rates (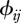), with the aid of community ecology.

(i). Species susceptibility (τ_i)

For a given pathogen, heterogeneity in species-specific infection success is empirically documented [13]; some species are highly vulnerable and can spread the disease easily (high susceptibility, 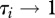), while others have a very low probability of infection and contribute little to pathogen transmission (tangential host, low susceptibility, ).

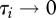We assume here that τ_i is a host's probability of becoming infected after exposure to an infectious individual (either con- or hetero-specific) and that it is identical across individuals within the same species. For purposes of model flexibility, we assume τ_i follows a truncated gamma distribution, with parameters k and ω.

(ii). Species abundance (N_i)

To overcome the potentially overwhelming complexity of host communities, we use well-known empirically derived laws inherited from community ecology to define basic patterns of species structure and abundance. To quantify the relationship between local abundance and species richness, we use the canonical Preston's law [29], generally applied to vertebrate host communities [30]. This law has been widely used for different systems across many taxonomic groups [31], and has a theoretical foundation [32]. It assumes a log-normal distribution of species richness across ‘octaves' of abundance, where one octave represents an abundance range (on a log₂ base) according to the following equation:

2.5

Here, s is the number of species in one octave distant P octaves from the mode, z is a constant calculated from field experiments (z < 1), and Y₀ is the number of species in the modal octave. This relationship is used for describing the host community structure in our model. Thus, the abundances modelled here will be the results of the species interactions at equilibrium (for the sake of simplicity, we assume constant host dynamics). Although recent theoretical studies have proposed different dominance–diversity relationships (see [33] in the context of tropical trees), we use Preston's law because of its statistical confirmation over a wide range of taxa [29,31].

(iii). Birth and death rates (b_i and d_i)

In order to analyse a wide range of host taxonomic groups with a range of body sizes, it is also crucial to consider their demographic rates. We assume that for any species, birth and death rates are identical (b_i = d_i) and are determined allometrically [34] by

2.6

where r_i is the per capita birth (and death) rate, and M_i the average body mass for a given species i. The distribution of average body mass can be modelled using the relationship described by Cohen and co-workers [35], which associates the body mass rank of each species (from the lightest to the heaviest species) to the mean body mass of each species as follows:

2.7

where M_i is the average body mass species, a and b two constants and j the body mass rank.

(iv). Matrix of contact rates (ϕ)

The final model component to define is the matrix of contact rates where 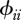represent intra-species contacts and 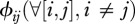corresponds to inter-species contacts. As a first step, we assume identical intra-specific contact rates across species (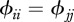) and symmetry in inter-specific contact rates ().

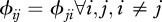(v). Links between distributions and additional assumptions

We assume that each octave in Preston's law represents a body mass rank and most abundant species have the lowest body mass, implying a fast demographic rate r_i () as usually observed [36]. Consistent with previous studies [17,37], we also assume that the most abundant species are the most susceptible. Since our main question could be reformulated on the impact of low susceptibility hosts on intensity of pathogen transmission, that leads to an underestimation of their potential effect and allows us to analyse the minimal influence exerted by this kind of host on disease dynamics. Finally, for tractability, we fix the infectious period for all species at 7 days.

(b). Impact of host community characteristics on disease dynamics

One possible way to understand disease transmission mechanisms within this framework is to compute the value of the basic reproduction ratio, or R₀, i.e. number of secondary infections caused by a single infectious individual in a population that is wholly susceptible [38]. This quantity, represented by the dominant eigenvalue of the next-generation matrix [39,40], is especially useful for determining whether a pathogen will invade a system. In our system, however, this approach would not paint the complete picture; we also need to measure quantitatively the impact of the structure of a species community on pathogen prevalence. Hence, we focus on the ‘peak disease prevalence’ across all host species (we calculate this using both the proportion as well as the number of infectious individuals). We use this quantity as an indicator of transmission intensity since it is linked with R₀, at least for the number of infectious individuals for a simple system with only one host species (see the electronic supplementary material). This measure will strongly depend on initial conditions, constraining us to apply the same initial conditions everywhere (all simulations start with one infectious individual in the most susceptible host species).

Since our system is non-linear with a large set of ordinary differential equations, analytical results are not feasible. Thus, we resort to numerical integration. For any parameter combination, the model is integrated for 100 years to analyse separately the impacts of three key determinants of community structure on these disease dynamics characteristics: (i) susceptibility distribution of host species, (ii) species community structure, in terms of evenness and richness, and (iii) shape of the contact matrix (analysis of host body mass distribution is given in the electronic supplementary material).

3. Results

(a). Impact of host species susceptibility distribution

Disease transmission is clearly modulated by the type(s) of host species constituting the local community and, more specifically, by their susceptibility. By keeping the other species community characteristics identical across simulations (such as species richness, abundance, contact patterns and demographic rates), we analyse the impact of susceptibility distribution on wildlife infectious disease dynamics.

We find that mean susceptibility within a host community drives the level of peak disease prevalence (figure 1). The replacement of a host species with another characterized by higher susceptibility will then enhance disease transmission.

Figure 1.

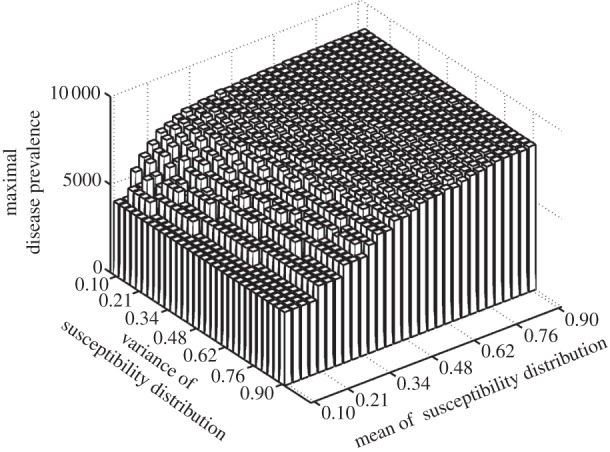
Relationship between susceptibility distribution (X-axis: mean, Y-axis: variance) and peak disease prevalence (Z-axis) within the whole community. Peak disease prevalence is defined here as the maximal number of infectious individuals observed during simulations (100 years). Parameters used: z = 0.1, Y₀ = 10, a = 0.6931, b = 0, 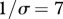days, 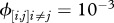, 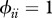. k and ω are modified to explore different forms of susceptibilities distribution.

By contrast, it is also clear that the variance in host susceptibility distribution does not influence peak disease prevalence (figure 1). Hence, for density-dependent transmitted diseases, two host communities with similar average susceptibility will show similar peak disease prevalences, irrespective of differences in the variance of susceptibility.

(b). Impact of host species community structure

Pathogens can circulate within host communities of various forms. For instance, a given characteristic (e.g. species richness) can be linked with different values of other parameters (such as abundance patterns). This results in contrasting community structures, modelled in this study through Preston's law, which may influence pathogen transmission in numerous ways. Here, we focus on the influence of community structure on peak disease prevalence by using a composite measure, i.e. their Shannon's index [41] as it is classically defined (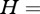 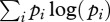where 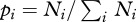), in order to make comparison possible between them.

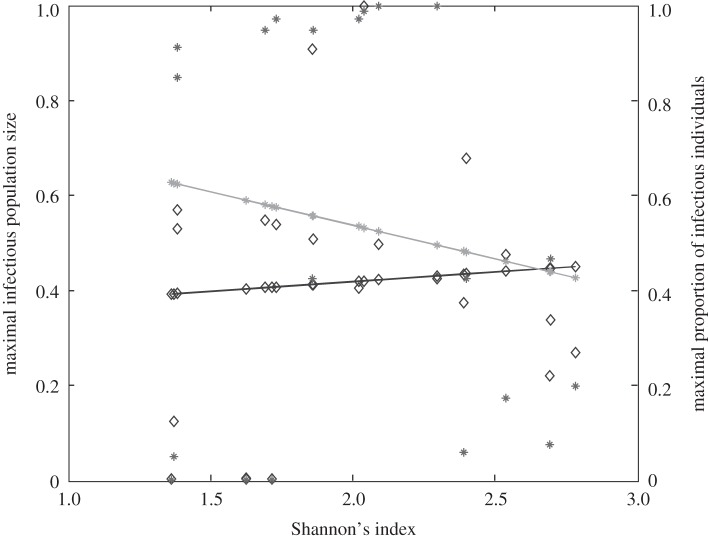
We find that total abundance of infectious individuals within the whole community increases with Shannon's index (figure 2, left Y-axis). If Preston's law drives the community structure, increasing Shannon's index leads, in most cases, to a greater total community abundance [42]. For density-dependent diseases, increasing abundance translates into higher transmission rate. This result has already been suggested for an increase in species richness [19,21], but never using Shannon's index with a realistic host community.

Figure 2.

Relationship between host species community characteristics (X-axis: Shannon's index, see the main text for mathematical formulation) and peak disease prevalence, in terms of abundance (left Y-axis; dark grey line and diamonds) and proportion (right Y-axis; light grey line and crosses) of infectious individuals. Both axes are rescaled between 0 and 1 for readability. Dark and light grey lines represent linear regressions and diamonds and crosses on these lines are the values predicted by linear regressions. Parameters used: a = 0.6931, b = 0, 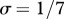days, 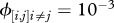, , 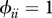, 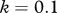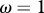. z and Y₀ are modified to explore different shapes of host community structures.

Conversely, the proportion (rather than the number) of infectious individuals' abundance within the whole community can show the opposite pattern (figure 2, right Y-axis). Since infectious abundance increases more slowly than total community abundance, a larger Shannon's index leads to more intense pathogen transmission, but to a lower overall proportion of infectious individuals.

(c). Impact of host species contact distribution

All previous results were based on the same inter-species and intra-species contact rates for every species, resulting in a homogeneous network of pathogen transmission between host species. This assumption is now relaxed and we analyse how different contact networks can alter disease dynamics.

Contact patterns may be modelled in numerous ways. For the sake of simplicity, we assume a hierarchical matrix that could be assimilated to a specific food-web in terms of network topology. We consider only two parameters. First, the inter-species contact rate (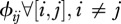) that quantifies the contact rate between species. We assume that all inter-species contact rates are identical and are different from the intra-species contact rate. The second parameter is the number of species connected between them (c). Each host species is ranked by its susceptibility and is connected to c species above it. Hence, when c increases, the number of connections between host species also increases (as illustrated by little diagrams on figure 3).

Figure 3.

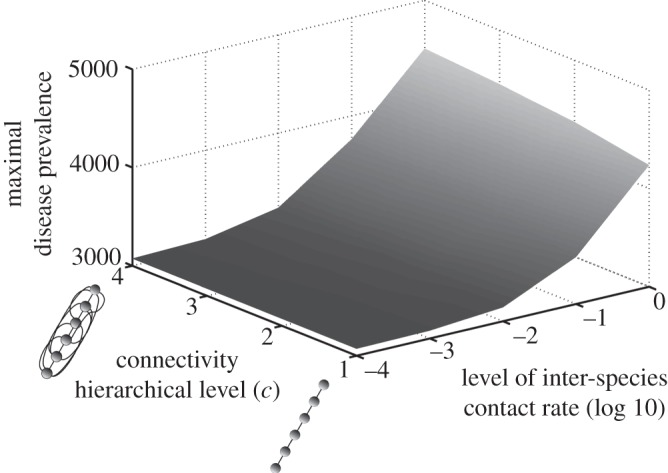
Influence of contact patterns between host species on peak disease prevalence. The small cartoons represent an example with different values of c (number of species connected to a single species). Parameters used: z = 0.1, Y₀ = 10, a = 0.6931, b = 0, 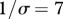days, k = 0.1, .

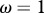We can observe the existence of a threshold for the global diffusion of a disease within a community (figure 3). The connectivity between host species seems to play a minor role when inter-species contact rate is high enough to link the most susceptible host species to the less susceptible one. This is explained by the hierarchical structure of the contact patterns and could be compared with a ‘cascade effect'.

4. Conclusions and discussion

In this paper, we have introduced a new theoretical approach to linking community and disease ecology. This framework has allowed us to study wildlife infections using large and empirically parameterized community assemblages. Consequently, we have been able to assess the respective transmission contributions of different aspects of host communities, i.e. species susceptibility, community structure and contact patterns.

Broadly, we have shown that an increase in host species diversity raises the number of infectious individuals, but decreases their proportion (figure 2). We have also highlighted that, with a simplified contact network, a pathogen could be spread globally within the host community if the inter-species transmission rate is sufficiently large, irrespective of the connectivity level between species (figure 3).

As with any modelling study of such a complex system, several assumptions were needed to make the analysis tractable. We have assumed that pathogen spread is only dependent on the species' susceptibility. However, disease transmission is not a ‘one-way’ process and some hosts can be infected, but never become infectious (they are classically named ‘dead-end’ or ‘tangential’ hosts). Here, we assume that this kind of host has a null susceptibility in order to under-estimate their influence on pathogen dynamics. Since our study can be reformulated for the role of low susceptible species on disease dynamics, underrating their influence makes our conclusions more robust.

It is worth pointing out that by using the SIR model, we have intentionally restricted our focus to infectious diseases that generate life-long immunity. In a number of systems, such as some rodent-borne diseases, immunity can be nonexistent or short-lived [43], with potential quantitative impacts on our conlusions. Addressing such a system would be an interesting extension of our study.

We have also assumed that the most abundant species are the most susceptible. This relationship, shown for Lyme disease in some locations of North America [13], may not be a general rule. Assessing the contribution of the link between species abundances and susceptibilities is therefore important to determine.

Similarly, we have focused here only on the epidemic's peak. This simplification allowed us to analyse the same quantity as sampled in the field and then to suggest a new mechanism to explain the observation of a dilution effect on density-dependent disease. Nevertheless, many other dynamical outputs should be explored to complete the picture, e.g. heterogeneity of prevalences, disease persistence or seasonality when host abundance will not be assumed constant.

Finally, a pragmatic assumption has been to assume a constant abundance of host species. This choice has been motivated by our wish to understand the core epidemiological mechanisms at play within a host community assemblage, rather than getting bogged down in attempts to match the population dynamics of each species, while simultaneously exploring the broader issues at hand.

The negative association observed in the field between high host species richness and low pathogen prevalence [22–24] has been called a ‘dilution effect’ despite theoretical studies predicting an increase in disease transmission in such a case [19,21]. Here, we show that, within the whole community, a decreasing prevalence and an increasing infectious population can be observed simultaneously. This explanation, reconciling theory and empirical observations without involving an ‘encounter reduction’, underlines that this empirical observation may simply be due to a misinterpretation of field data and is possibly not a dilution effect stricto sensu.

Nevertheless, this process could closely be related to a dilution effect if we consider only outcomes on public health. Indeed, our study suggests that community structure would have different impacts on human pathogen exposure regarding the transmission process between wildlife and humans, i.e. the strong influence of the shape of this transmission route has already been highlighted for pathogen adaptation to humans [44,45]. If these contacts are density-dependent, an increase in host species richness leads to a higher human risk. Conversely, if these contacts are frequency-dependent (when contact frequency is not altered by host abundance), the transmission risk to human populations will be lower because human exposure will be driven by the proportion of infectious animals instead of their absolute number. This result has a broad public health impact since adding host species with a low susceptibility has been suggested to decrease human exposure to any given pathogen (i.e. zooprophylaxis, Saul [46]). Indeed, understanding the contact processes between wildlife and humans is mandatory before the consideration of applying such an approach.

The constraints exerted by the community context on the relationship between species richness and abundance have a profound impact on pathogen spillover and should be clearly considered. This is especially important for emerging infections that have, as a general rule, a low host specificity [8]. We have decided to study first the case of density-dependent diseases because of their simplicity in terms of life cycle. Another natural next step should be to extend this framework to pathogens exhibiting different, more complex, transmission processes. This way, we can take further steps to figure out the overwhelming complexity of zoonotic infectious diseases and the risk of their spillover as extinctions continue at an alarming rate.