Abstract
The increasing number of zoonotic diseases spilling over from a range of wild animal species represents a particular concern for public health, especially in light of the current dramatic trend of biodiversity loss. To understand the ecology of these multi-host pathogens and their response to environmental degradation and species extinctions, it is necessary to develop a theoretical framework that takes into account realistic community assemblages. Here, we present a multi-host species epidemiological model that includes empirically determined patterns of diversity and composition derived from community ecology studies. We use this framework to study the interaction between wildlife diversity and directly transmitted pathogen dynamics. First, we demonstrate that variability in community composition does not affect significantly the intensity of pathogen transmission. We also show that the consequences of community diversity can differentially impact the prevalence of pathogens and the number of infectious individuals. Finally, we show that ecological interactions among host species have a weaker influence on pathogen circulation than inter-species transmission rates. We conclude that integration of a community perspective to study wildlife pathogens is crucial, especially in the context of understanding and predicting infectious disease emergence events.
Keywords: community epidemiology, density-dependent infectious diseases, community ecology, mathematical modelling
1. Introduction
For more than a century, there has been an exciting and mutually beneficial interplay between epidemiological theory and empirical research [1,2]. This has led to a deep understanding of host–pathogen interactions and the impact of a wide range of complexities that determine and affect transmission dynamics and host ecology. Much of this progress has been achieved, however, for systems with a substantially simplified ecology, with perhaps a disproportionately large focus on infectious diseases of humans and livestock [2–4]. The recent rise of zoonotic emerging infectious diseases [5–7] has increased our awareness of the ecological context of infectious diseases and has highlighted the chasm between standard theory and biological reality. We argue that what is called for is greater ecological sophistication in our epidemiological theory if we aim to explain zoonoses [8], identify the determinants of pathogen spillover [9–11] and understand the reciprocal impacts of infectious diseases and biodiversity [12–18].
The disconnect between current theory and empirical observations may be illustrated simply for directly transmitted pathogens. Dobson [19] explored host–pathogen community assemblages assuming density-dependent transmission (whereby an increase in host abundance results in an increase in the transmission rate owing to increased contact [2,20]). The consequences on transmission of introducing a novel species to the host community was found to depend not only on its relative susceptibility, but also on the competitive interactions in the host assemblage [21]. Assuming a simplified host community, with host abundances derived from allometric laws, Dobson [19] confirmed mathematically that transmission is amplified whenever the introduced species is assumed to increase overall host density or if it replaces a less susceptible species [21]. By contrast, empirical studies on rodent-borne diseases [22–24], assumed to be spread through density-dependent transmission, suggest that increased host species richness is associated with lower pathogen prevalence. The proposed explanation centres on ‘encounter reduction’, i.e. a decrease in contacts with the most susceptible species because of newly introduced hosts [10], and suggests that ecological interactions are a main component of pathogen transmission.
Here, in a bid to better link community ecology [25] and disease ecology [26,27], we propose a novel theoretical framework. It is composed of multiple host species, where species abundances are derived from empirical abundance relationships. We examine this model in the context of diseases with density-dependent transmission in order to assess how host community composition and diversity affect pathogen circulation. Overall, we demonstrate that variability in community composition, i.e. susceptibility of host species, does not qualitatively affect pathogen transmission. An increase in host species richness, however, can yield a greater number of infectious individuals, while simultaneously reducing their frequency in the whole host community (in other words, their prevalence). We discuss the implications of these results, especially in the context of rodent-borne diseases where the observation of reduced, or diluted, infection prevalence can—we submit—be a misinterpretation of empirical data. We conclude that considering a community perspective may give critical insights into epidemiological patterns reported for wildlife infections and may help to anticipate their dynamics.
2. Material and methods
We assume that pathogen dynamics is described by a classical Susceptible, Infectious and Recovered (SIR) model [2,4,26], which takes into account the possibility of multiple host species:
| 2.1 |
| 2.2 |
| 2.3 |
Each of the n host species is denoted by subscript i. The abundance of host species, Ni, is divided into three groups according to their infection status. At a per capita rate, bi, immunologically naive individuals are born into the Susceptible class (Si). Upon transmission, they become Infectious (Ii) and may subsequently transmit the pathogen to con- and hetero-specifics. At rate  , infecteds move to the Recovered class (Ri), and are assumed immune for life. Finally, individuals are assumed to die at a constant rate, di, irrespective of their infection status.
, infecteds move to the Recovered class (Ri), and are assumed immune for life. Finally, individuals are assumed to die at a constant rate, di, irrespective of their infection status.
The per capita transmission hazard is determined by the ‘force of infection’, λi. We assume here density-dependent transmission, thought to be appropriate for directly transmitted pathogens among wildlife [4,28] or humans [2], leading to:
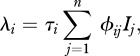 |
2.4 |
where n represents host species richness, τi the susceptibility of species i (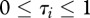 ),
), 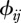 the contact rate between species j and species i and Ij the number of infectious individuals from species j.
the contact rate between species j and species i and Ij the number of infectious individuals from species j.
(a). Integrating ecological realism
We assume that host species comprise a community of vertebrate animals. To study realistic host community configurations, we quantify species ecology, i.e. their susceptibilities (τi), abundances (Ni), demographic rates (bi and di) and heterospecific contact rates (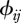 ), with the aid of community ecology.
), with the aid of community ecology.
(i). Species susceptibility (τi)
For a given pathogen, heterogeneity in species-specific infection success is empirically documented [13]; some species are highly vulnerable and can spread the disease easily (high susceptibility, 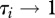 ), while others have a very low probability of infection and contribute little to pathogen transmission (tangential host, low susceptibility,
), while others have a very low probability of infection and contribute little to pathogen transmission (tangential host, low susceptibility, 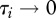 ).
).
We assume here that τi is a host's probability of becoming infected after exposure to an infectious individual (either con- or hetero-specific) and that it is identical across individuals within the same species. For purposes of model flexibility, we assume τi follows a truncated gamma distribution, with parameters k and ω.
(ii). Species abundance (Ni)
To overcome the potentially overwhelming complexity of host communities, we use well-known empirically derived laws inherited from community ecology to define basic patterns of species structure and abundance. To quantify the relationship between local abundance and species richness, we use the canonical Preston's law [29], generally applied to vertebrate host communities [30]. This law has been widely used for different systems across many taxonomic groups [31], and has a theoretical foundation [32]. It assumes a log-normal distribution of species richness across ‘octaves' of abundance, where one octave represents an abundance range (on a log2 base) according to the following equation:
| 2.5 |
Here, s is the number of species in one octave distant P octaves from the mode, z is a constant calculated from field experiments (z < 1), and Y0 is the number of species in the modal octave. This relationship is used for describing the host community structure in our model. Thus, the abundances modelled here will be the results of the species interactions at equilibrium (for the sake of simplicity, we assume constant host dynamics). Although recent theoretical studies have proposed different dominance–diversity relationships (see [33] in the context of tropical trees), we use Preston's law because of its statistical confirmation over a wide range of taxa [29,31].
(iii). Birth and death rates (bi and di)
In order to analyse a wide range of host taxonomic groups with a range of body sizes, it is also crucial to consider their demographic rates. We assume that for any species, birth and death rates are identical (bi = di) and are determined allometrically [34] by
| 2.6 |
where ri is the per capita birth (and death) rate, and Mi the average body mass for a given species i. The distribution of average body mass can be modelled using the relationship described by Cohen and co-workers [35], which associates the body mass rank of each species (from the lightest to the heaviest species) to the mean body mass of each species as follows:
| 2.7 |
where Mi is the average body mass species, a and b two constants and j the body mass rank.
(iv). Matrix of contact rates (ϕ)
The final model component to define is the matrix of contact rates where 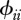 represent intra-species contacts and
represent intra-species contacts and 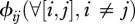 corresponds to inter-species contacts. As a first step, we assume identical intra-specific contact rates across species (
corresponds to inter-species contacts. As a first step, we assume identical intra-specific contact rates across species (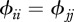 ) and symmetry in inter-specific contact rates (
) and symmetry in inter-specific contact rates (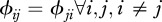 ).
).
(v). Links between distributions and additional assumptions
We assume that each octave in Preston's law represents a body mass rank and most abundant species have the lowest body mass, implying a fast demographic rate ri ( ) as usually observed [36]. Consistent with previous studies [17,37], we also assume that the most abundant species are the most susceptible. Since our main question could be reformulated on the impact of low susceptibility hosts on intensity of pathogen transmission, that leads to an underestimation of their potential effect and allows us to analyse the minimal influence exerted by this kind of host on disease dynamics. Finally, for tractability, we fix the infectious period for all species at 7 days.
) as usually observed [36]. Consistent with previous studies [17,37], we also assume that the most abundant species are the most susceptible. Since our main question could be reformulated on the impact of low susceptibility hosts on intensity of pathogen transmission, that leads to an underestimation of their potential effect and allows us to analyse the minimal influence exerted by this kind of host on disease dynamics. Finally, for tractability, we fix the infectious period for all species at 7 days.
(b). Impact of host community characteristics on disease dynamics
One possible way to understand disease transmission mechanisms within this framework is to compute the value of the basic reproduction ratio, or R0, i.e. number of secondary infections caused by a single infectious individual in a population that is wholly susceptible [38]. This quantity, represented by the dominant eigenvalue of the next-generation matrix [39,40], is especially useful for determining whether a pathogen will invade a system. In our system, however, this approach would not paint the complete picture; we also need to measure quantitatively the impact of the structure of a species community on pathogen prevalence. Hence, we focus on the ‘peak disease prevalence’ across all host species (we calculate this using both the proportion as well as the number of infectious individuals). We use this quantity as an indicator of transmission intensity since it is linked with R0, at least for the number of infectious individuals for a simple system with only one host species (see the electronic supplementary material). This measure will strongly depend on initial conditions, constraining us to apply the same initial conditions everywhere (all simulations start with one infectious individual in the most susceptible host species).
Since our system is non-linear with a large set of ordinary differential equations, analytical results are not feasible. Thus, we resort to numerical integration. For any parameter combination, the model is integrated for 100 years to analyse separately the impacts of three key determinants of community structure on these disease dynamics characteristics: (i) susceptibility distribution of host species, (ii) species community structure, in terms of evenness and richness, and (iii) shape of the contact matrix (analysis of host body mass distribution is given in the electronic supplementary material).
3. Results
(a). Impact of host species susceptibility distribution
Disease transmission is clearly modulated by the type(s) of host species constituting the local community and, more specifically, by their susceptibility. By keeping the other species community characteristics identical across simulations (such as species richness, abundance, contact patterns and demographic rates), we analyse the impact of susceptibility distribution on wildlife infectious disease dynamics.
We find that mean susceptibility within a host community drives the level of peak disease prevalence (figure 1). The replacement of a host species with another characterized by higher susceptibility will then enhance disease transmission.
Figure 1.
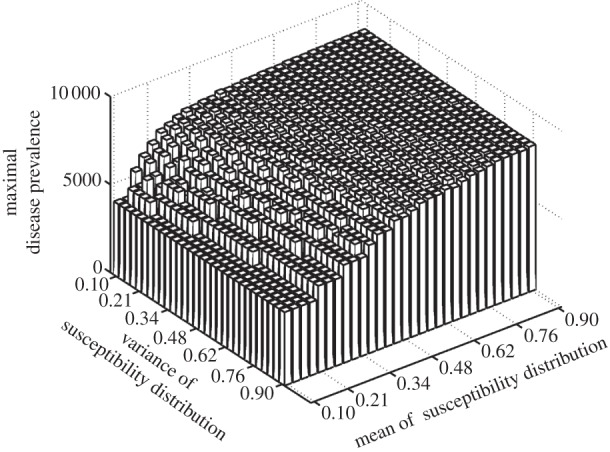
Relationship between susceptibility distribution (X-axis: mean, Y-axis: variance) and peak disease prevalence (Z-axis) within the whole community. Peak disease prevalence is defined here as the maximal number of infectious individuals observed during simulations (100 years). Parameters used: z = 0.1, Y0 = 10, a = 0.6931, b = 0, 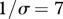 days,
days, 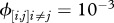 ,
, 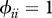 . k and ω are modified to explore different forms of susceptibilities distribution.
. k and ω are modified to explore different forms of susceptibilities distribution.
By contrast, it is also clear that the variance in host susceptibility distribution does not influence peak disease prevalence (figure 1). Hence, for density-dependent transmitted diseases, two host communities with similar average susceptibility will show similar peak disease prevalences, irrespective of differences in the variance of susceptibility.
(b). Impact of host species community structure
Pathogens can circulate within host communities of various forms. For instance, a given characteristic (e.g. species richness) can be linked with different values of other parameters (such as abundance patterns). This results in contrasting community structures, modelled in this study through Preston's law, which may influence pathogen transmission in numerous ways. Here, we focus on the influence of community structure on peak disease prevalence by using a composite measure, i.e. their Shannon's index [41] as it is classically defined (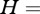
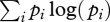 where
where 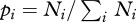 ), in order to make comparison possible between them.
), in order to make comparison possible between them.
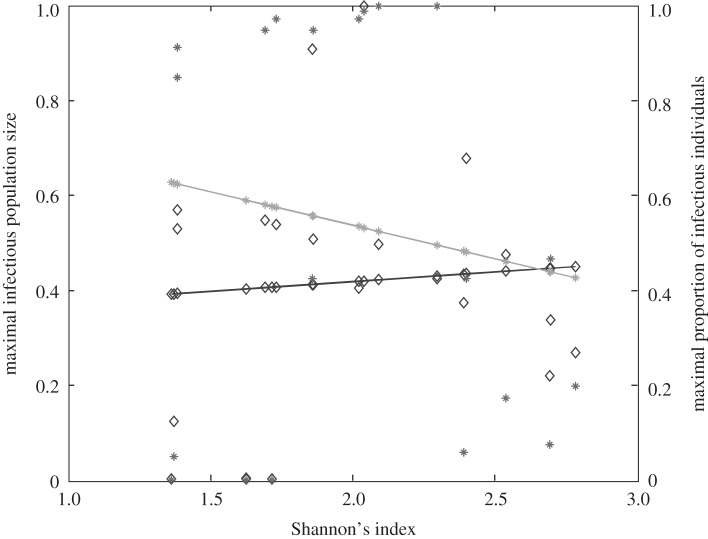
We find that total abundance of infectious individuals within the whole community increases with Shannon's index (figure 2, left Y-axis). If Preston's law drives the community structure, increasing Shannon's index leads, in most cases, to a greater total community abundance [42]. For density-dependent diseases, increasing abundance translates into higher transmission rate. This result has already been suggested for an increase in species richness [19,21], but never using Shannon's index with a realistic host community.
Figure 2.
Relationship between host species community characteristics (X-axis: Shannon's index, see the main text for mathematical formulation) and peak disease prevalence, in terms of abundance (left Y-axis; dark grey line and diamonds) and proportion (right Y-axis; light grey line and crosses) of infectious individuals. Both axes are rescaled between 0 and 1 for readability. Dark and light grey lines represent linear regressions and diamonds and crosses on these lines are the values predicted by linear regressions. Parameters used: a = 0.6931, b = 0, 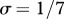 days,
days, 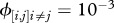 ,
, 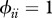 ,
, 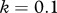 ,
, 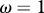 . z and Y0 are modified to explore different shapes of host community structures.
. z and Y0 are modified to explore different shapes of host community structures.
Conversely, the proportion (rather than the number) of infectious individuals' abundance within the whole community can show the opposite pattern (figure 2, right Y-axis). Since infectious abundance increases more slowly than total community abundance, a larger Shannon's index leads to more intense pathogen transmission, but to a lower overall proportion of infectious individuals.
(c). Impact of host species contact distribution
All previous results were based on the same inter-species and intra-species contact rates for every species, resulting in a homogeneous network of pathogen transmission between host species. This assumption is now relaxed and we analyse how different contact networks can alter disease dynamics.
Contact patterns may be modelled in numerous ways. For the sake of simplicity, we assume a hierarchical matrix that could be assimilated to a specific food-web in terms of network topology. We consider only two parameters. First, the inter-species contact rate (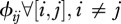 ) that quantifies the contact rate between species. We assume that all inter-species contact rates are identical and are different from the intra-species contact rate. The second parameter is the number of species connected between them (c). Each host species is ranked by its susceptibility and is connected to c species above it. Hence, when c increases, the number of connections between host species also increases (as illustrated by little diagrams on figure 3).
) that quantifies the contact rate between species. We assume that all inter-species contact rates are identical and are different from the intra-species contact rate. The second parameter is the number of species connected between them (c). Each host species is ranked by its susceptibility and is connected to c species above it. Hence, when c increases, the number of connections between host species also increases (as illustrated by little diagrams on figure 3).
Figure 3.
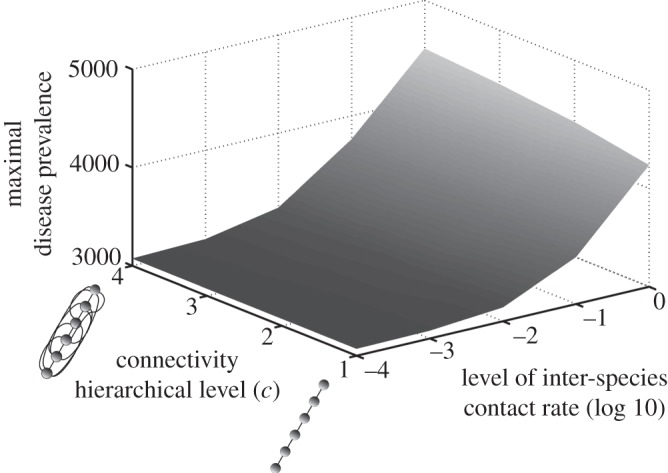
Influence of contact patterns between host species on peak disease prevalence. The small cartoons represent an example with different values of c (number of species connected to a single species). Parameters used: z = 0.1, Y0 = 10, a = 0.6931, b = 0, 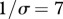 days, k = 0.1,
days, k = 0.1, 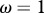 .
.
We can observe the existence of a threshold for the global diffusion of a disease within a community (figure 3). The connectivity between host species seems to play a minor role when inter-species contact rate is high enough to link the most susceptible host species to the less susceptible one. This is explained by the hierarchical structure of the contact patterns and could be compared with a ‘cascade effect'.
4. Conclusions and discussion
In this paper, we have introduced a new theoretical approach to linking community and disease ecology. This framework has allowed us to study wildlife infections using large and empirically parameterized community assemblages. Consequently, we have been able to assess the respective transmission contributions of different aspects of host communities, i.e. species susceptibility, community structure and contact patterns.
Broadly, we have shown that an increase in host species diversity raises the number of infectious individuals, but decreases their proportion (figure 2). We have also highlighted that, with a simplified contact network, a pathogen could be spread globally within the host community if the inter-species transmission rate is sufficiently large, irrespective of the connectivity level between species (figure 3).
As with any modelling study of such a complex system, several assumptions were needed to make the analysis tractable. We have assumed that pathogen spread is only dependent on the species' susceptibility. However, disease transmission is not a ‘one-way’ process and some hosts can be infected, but never become infectious (they are classically named ‘dead-end’ or ‘tangential’ hosts). Here, we assume that this kind of host has a null susceptibility in order to under-estimate their influence on pathogen dynamics. Since our study can be reformulated for the role of low susceptible species on disease dynamics, underrating their influence makes our conclusions more robust.
It is worth pointing out that by using the SIR model, we have intentionally restricted our focus to infectious diseases that generate life-long immunity. In a number of systems, such as some rodent-borne diseases, immunity can be nonexistent or short-lived [43], with potential quantitative impacts on our conlusions. Addressing such a system would be an interesting extension of our study.
We have also assumed that the most abundant species are the most susceptible. This relationship, shown for Lyme disease in some locations of North America [13], may not be a general rule. Assessing the contribution of the link between species abundances and susceptibilities is therefore important to determine.
Similarly, we have focused here only on the epidemic's peak. This simplification allowed us to analyse the same quantity as sampled in the field and then to suggest a new mechanism to explain the observation of a dilution effect on density-dependent disease. Nevertheless, many other dynamical outputs should be explored to complete the picture, e.g. heterogeneity of prevalences, disease persistence or seasonality when host abundance will not be assumed constant.
Finally, a pragmatic assumption has been to assume a constant abundance of host species. This choice has been motivated by our wish to understand the core epidemiological mechanisms at play within a host community assemblage, rather than getting bogged down in attempts to match the population dynamics of each species, while simultaneously exploring the broader issues at hand.
The negative association observed in the field between high host species richness and low pathogen prevalence [22–24] has been called a ‘dilution effect’ despite theoretical studies predicting an increase in disease transmission in such a case [19,21]. Here, we show that, within the whole community, a decreasing prevalence and an increasing infectious population can be observed simultaneously. This explanation, reconciling theory and empirical observations without involving an ‘encounter reduction’, underlines that this empirical observation may simply be due to a misinterpretation of field data and is possibly not a dilution effect stricto sensu.
Nevertheless, this process could closely be related to a dilution effect if we consider only outcomes on public health. Indeed, our study suggests that community structure would have different impacts on human pathogen exposure regarding the transmission process between wildlife and humans, i.e. the strong influence of the shape of this transmission route has already been highlighted for pathogen adaptation to humans [44,45]. If these contacts are density-dependent, an increase in host species richness leads to a higher human risk. Conversely, if these contacts are frequency-dependent (when contact frequency is not altered by host abundance), the transmission risk to human populations will be lower because human exposure will be driven by the proportion of infectious animals instead of their absolute number. This result has a broad public health impact since adding host species with a low susceptibility has been suggested to decrease human exposure to any given pathogen (i.e. zooprophylaxis, Saul [46]). Indeed, understanding the contact processes between wildlife and humans is mandatory before the consideration of applying such an approach.
The constraints exerted by the community context on the relationship between species richness and abundance have a profound impact on pathogen spillover and should be clearly considered. This is especially important for emerging infections that have, as a general rule, a low host specificity [8]. We have decided to study first the case of density-dependent diseases because of their simplicity in terms of life cycle. Another natural next step should be to extend this framework to pathogens exhibiting different, more complex, transmission processes. This way, we can take further steps to figure out the overwhelming complexity of zoonotic infectious diseases and the risk of their spillover as extinctions continue at an alarming rate.
Acknowledgements
We sincerely acknowledge the many colleagues who reviewed and improved this manuscript. In particular, we thank Marc Choisy, Camille Lebarbenchon, Andrew Park, John Drake, Krisztian Magori, Peter Daszak, Rick Ostfeld, the Rohani and King laboratories at the University of Michigan for their helpful comments. B.R. and J.F.G. are sponsored by the Institut de Recherche pour le Développement and the Centre National de la Recherche Scientifique, the French School of Public Health and acknowledge support from the EDEN project (EU grant GOCE2003010284 EDEN). P.R. was supported by the RAPIDD program of the Science and Technology Directorate, Department of Homeland Security, and the Fogarty International Center, National Institutes of Health. This publication is catalogued by the EDEN Steering Committee as EDEN089 (http://www.edenfp6project.net/). The contents of this publication are the sole responsibility of the authors and do not necessarily reflect the views of the European Commission. This work is a contribution from DIVERSITAS-EcoHealth Alliance ecoHEALTH research working group and the LABEX CEBA ANR-10-LABX-25-01.
References
- 1.Kermak W., McKendrik A. 1927. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 115, 700–726 10.1098/rspa.1927.0118 (doi:10.1098/rspa.1927.0118) [DOI] [Google Scholar]
- 2.Anderson R. M., May R. M. 1991. Infectious diseases of humans: dynamics and control. Oxford, UK: Oxford Science Publications [Google Scholar]
- 3.Grenfell B. T., Bjornstad O. N., Kappey J. 2001. Travelling waves and spatial hierarchies in measles epidemics. Nature 414, 716–723 10.1038/414716a (doi:10.1038/414716a) [DOI] [PubMed] [Google Scholar]
- 4.Keeling M. J., Rohani P. 2008. Modeling infectious diseases in humans and animals. Princeton, NJ: Princeton University Press [Google Scholar]
- 5.Daszak P., Cunningham A. A., Hyatt A. D. 2001. Anthropogenic environmental change and the emergence of infectious diseases in wildlife. Acta Trop. 78, 103–116 10.1016/S0001-706X(00)00179-0 (doi:10.1016/S0001-706X(00)00179-0) [DOI] [PubMed] [Google Scholar]
- 6.Taylor L. H., Latham S. M., Woolhouse M. E. 2001. Risk factors for human disease emergence. Phil. Trans. R. Soc. Lond. B 356, 983–989 10.1098/rstb.2001.0888 (doi:10.1098/rstb.2001.0888) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jones K. E., Patel N. G., Levy M. A., Storeygard A., Balk D., Gittleman J. L., Daszak P. 2008. Global trends in emerging infectious diseases. Nature 451, 990–994 10.1038/nature06536 (doi:10.1038/nature06536) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Woolhouse M. E. J., Gowtage-Sequeria S. 2005. Host range and emerging and reemerging pathogens. Emerg. Infect. Dis. 11, 1842–1847 10.3201/eid1112.050997 (doi:10.3201/eid1112.050997) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Begon M., Hazel S. M., Baxby D., Bown K., Cavanagh R., Chantrey J., Jones T., Bennett M. 1999. Transmission dynamics of a zoonotic pathogen within and between wildlife host species. Proc R. Soc. Lond. B 266, 1939–1945 10.1098/rspb.1999.0870 (doi:10.1098/rspb.1999.0870) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Keesing F., Holt R., Ostfeld R. 2006. Effects of species diversity on disease risk. Ecol. Lett. 9, 485–498 10.1111/j.1461-0248.2006.00885.x (doi:10.1111/j.1461-0248.2006.00885.x) [DOI] [PubMed] [Google Scholar]
- 11.Dobson A., Cattadori I., Holt R. D., Ostfeld R. S., Keesing F., Krichbaum K., Rohr J. R., Perkins S. E., Hudson P. J. 2006. Sacred cows and sympathetic squirrels: the importance of biological diversity to human health. PLoS Med. 3, e231. 10.1371/journal.pmed.0030231 (doi:10.1371/journal.pmed.0030231) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Balvanera P., Pfisterer A. B., Buchmann N., He J.-S., Nakashizuka T., Raffaelli D., Schmidt B. 2006. Quantifying the evidence for biodiversity effects on ecosystem functioning and services. Ecol. Lett. 9, 1–11 10.1111/j.1461-0248.2006.00963.x (doi:10.1111/j.1461-0248.2006.00963.x) [DOI] [PubMed] [Google Scholar]
- 13.LoGiudice K., Ostfeld R. S., Schmidt K. A., Keesing F. 2003. The ecology of infectious disease: effects of host diversity and community composition on Lyme disease risk. Proc. Natl Acad. Sci. USA 100, 567–571 10.1073/pnas.0233733100 (doi:10.1073/pnas.0233733100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Garrett K. A., Mundt C. C. 1999. Epidemiology in mixed host populations. Phytopathology 89, 984–990 10.1094/PHYTO.1999.89.11.984 (doi:10.1094/PHYTO.1999.89.11.984) [DOI] [PubMed] [Google Scholar]
- 15.Allan B. F., Keesing F., Ostfeld R. S. 2003. Effect of forest fragmentation on Lyme disease risk. Conserv. Biol. 17, 267–272 10.1046/j.1523-1739.2003.01260.x (doi:10.1046/j.1523-1739.2003.01260.x) [DOI] [Google Scholar]
- 16.LoGiudice K., Duerr S. T. K., Newhouse M. J., Schmidt K. A., Killilea M. E., Ostfeld R. S. 2008. Impact of host community composition on Lyme disease risk. Ecology 89, 2841–2849 10.1890/07-1047.1 (doi:10.1890/07-1047.1) [DOI] [PubMed] [Google Scholar]
- 17.Ostfeld R. S., Keesing F. 2000. The function of biodiversity in the ecology of vector-borne zoonotic diseases. Can. J. Zool. 78, 2061–2078 10.1139/z00-172 (doi:10.1139/z00-172) [DOI] [Google Scholar]
- 18.Keesing F., et al. 2010. Impacts of biodiversity on the emergence and transmission of infectious diseases. Nature 468, 647–652 10.1038/nature09575 (doi:10.1038/nature09575) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dobson A. 2004. Population dynamics of pathogens with multiple host species. Am. Nat. 164, S64–S78 10.1086/424681 (doi:10.1086/424681) [DOI] [PubMed] [Google Scholar]
- 20.McCallum H., Barlow N., Hone J. 2001. How should pathogen transmission be modelled? Trends Ecol. Evol. 16, 295–300 10.1016/S0169-5347(01)02144-9 (doi:10.1016/S0169-5347(01)02144-9) [DOI] [PubMed] [Google Scholar]
- 21.Rudolf V. H. W., Antonovics J. 2005. Species coexistence and pathogens with frequency-dependent transmission. Am. Nat. 166, 112–118 10.1086/430674 (doi:10.1086/430674) [DOI] [PubMed] [Google Scholar]
- 22.Tersago K., Schreurs A., Linard C., Verhagen R., Dongen S. V., Leirs H. 2008. Population, environmental, and community effects on local bank vole (Myodes glareolus) puumala virus infection in an area with low human incidence. Vector Borne Zoonotic Dis. 8, 235–244 10.1089/vbz.2007.0160 (doi:10.1089/vbz.2007.0160) [DOI] [PubMed] [Google Scholar]
- 23.Mills J. N., Ksiazek T. G., Peters C. J., Childs J. E. 1999. Long-term studies of hantavirus reservoir populations in the southwestern United States: a synthesis. Emerg. Infect. Dis. 5, 135–142 10.3201/eid0501.990116 (doi:10.3201/eid0501.990116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Clay C. A., Lehmer E. M., Jeor S. S., Dearing M. D. 2009. Testing mechanisms of the dilution effect: deer mice encounter rates, sin nombre virus prevalence and species diversity. Ecohealth 6, 250–259 10.1007/s10393-009-0240-2 (doi:10.1007/s10393-009-0240-2) [DOI] [PubMed] [Google Scholar]
- 25.Putman R. J. 1994. Community ecology. Berlin, Germany: Springer [Google Scholar]
- 26.Grenfell B. T., Dobson A. P. (eds) 1995. Ecology of infectious diseases in natural populations. Cambridge, UK: Cambridge University Press [Google Scholar]
- 27.Ostfeld R. S., Keesing F., Eviner V. T. (eds) 2008. Infectious disease ecology: effects of ecosystems on disease and of disease on ecosystems. Princeton, NJ: Princeton University Press [Google Scholar]
- 28.Lloyd-Smith J. O., Cross P. C., Briggs C. J., Daugherty M., Getz W. M., Latto J., Sanchez M. S., Smith A. B., Swei A. 2005. Should we expect population threshold for wildlife disease? Trends Ecol. Evol. 20, 511–519 10.1016/j.tree.2005.07.004 (doi:10.1016/j.tree.2005.07.004) [DOI] [PubMed] [Google Scholar]
- 29.Preston F. W. 1948. The commonness, and rarity, of species. Ecology 29, 254–283 10.2307/1930989 (doi:10.2307/1930989) [DOI] [Google Scholar]
- 30.Bell G. 2001. Neutral macroecology. Science 293, 2413–2418 10.1126/science.293.5539.2413 (doi:10.1126/science.293.5539.2413) [DOI] [PubMed] [Google Scholar]
- 31.Preston F. W. 1962. The canonical distribution of commonness and rarity: part I. Ecology 43, 185–215 10.2307/1931976 (doi:10.2307/1931976) [DOI] [Google Scholar]
- 32.May R. M. 1975. Patterns of species abundance and diversity, ch. 4, pp. 81–120 Harvard, MA: Harvard University Press [Google Scholar]
- 33.Hubbell S. P. 2001. The unified neutral theory of biodiversity and biogeography. Princeton, NJ: Princeton University Press [Google Scholar]
- 34.DeLeo G. A., Dobson A. P. 1996. Allometry and simple epidemic models for microparasites. Nature 379, 720–722 10.1038/379720a0 (doi:10.1038/379720a0) [DOI] [PubMed] [Google Scholar]
- 35.Cohen J. E., Jonsson T., Carpenter S. R. 2003. Ecological community description using the food web, species abundance, and body size. Proc. Natl Acad. Sci. USA 100, 1781–1786 10.1073/pnas.232715699 (doi:10.1073/pnas.232715699) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Damuth J. 1981. Population density and body size in mammals. Nature 290, 699–700 10.1038/290699a0 (doi:10.1038/290699a0) [DOI] [Google Scholar]
- 37.Ostfeld R. S., Keesing F. 2000. Biodiversity and disease risk: the case of Lyme disease. Conserv. Biol. 14, 722–728 10.1046/j.1523-1739.2000.99014.x (doi:10.1046/j.1523-1739.2000.99014.x) [DOI] [Google Scholar]
- 38.Heesterbeek H. 2002. A brief history of r0 and a recipe for its calculation. Acta Biotheoretica 50, 189–204 10.1023/A:1016599411804 (doi:10.1023/A:1016599411804) [DOI] [PubMed] [Google Scholar]
- 39.Diekmann O., Heesterbeek J. A., Metz J. A. 1990. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382 10.1007/BF00178324 (doi:10.1007/BF00178324) [DOI] [PubMed] [Google Scholar]
- 40.van den Driessche P., Watmough J. 2002. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 10.1016/S0025-5564(02)00108-6 (doi:10.1016/S0025-5564(02)00108-6) [DOI] [PubMed] [Google Scholar]
- 41.Shannon C. E. 1948. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 [Google Scholar]
- 42.May R. M. 1975. Biological populations obeying difference equations: stable points, stable cycles, and chaos. J. Theoret. Biol. 51, 511–524 10.1016/0022-5193(75)90078-8 (doi:10.1016/0022-5193(75)90078-8) [DOI] [PubMed] [Google Scholar]
- 43.Schmaljohn C., Hjelle B. 1997. Hantaviruses: a global disease problem. Emerg. Infect. Dis. 3, 95–104 10.3201/eid0302.970202 (doi:10.3201/eid0302.970202) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wolf M., van Doorn G. S., Leimar O., Weissing F. J. 2007. Life-history trade-offs favour the evolution of animal personalities. Nature 447, 581–584 10.1038/nature05835 (doi:10.1038/nature05835) [DOI] [PubMed] [Google Scholar]
- 45.Lloyd-Smith J. O., George D., Pepin K. M., Pitzer V. E., Pulliam J. R. C., Dobson A. P., Hudson P. J., Grenfell B. T. 2009. Epidemic dynamics at the human–animal interface. Science 326, 1362–1367 10.1126/science.1177345 (doi:10.1126/science.1177345) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Saul A. 2003. Zooprophylaxis or zoopotentiation: the outcome of introducing animals on vector transmission is highly dependent on the mosquito mortality while searching. Malaria J. 2, 32. 10.1186/1475-2875-2-32 (doi:10.1186/1475-2875-2-32) [DOI] [PMC free article] [PubMed] [Google Scholar]