Variability in solar radiation and temperature explains observed patterns and trends in tree growth rates across four tropical forests

Abstract

The response of tropical forests to global climate variability and change remains poorly understood. Results from long-term studies of permanent forest plots have reported different, and in some cases opposing trends in tropical forest dynamics. In this study, we examined changes in tree growth rates at four long-term permanent tropical forest research plots in relation to variation in solar radiation, temperature and precipitation. Temporal variation in the stand-level growth rates measured at five-year intervals was found to be positively correlated with variation in incoming solar radiation and negatively related to temporal variation in night-time temperatures. Taken alone, neither solar radiation variability nor the effects of night-time temperatures can account for the observed temporal variation in tree growth rates across sites, but when considered together, these two climate variables account for most of the observed temporal variability in tree growth rates. Further analysis indicates that the stand-level response is primarily driven by the responses of smaller-sized trees (less than 20 cm in diameter). The combined temperature and radiation responses identified in this study provide a potential explanation for the conflicting patterns in tree growth rates found in previous studies.

1. Introduction

Although trends in environmental forcing over the tropical regions, including temperature, atmospheric CO₂, solar radiation, and precipitation, have been recognized [1,2], the responses of tropical forests to current and future global climate change remain poorly understood. There is ongoing debate about whether tropical forests are likely to become net carbon sources or sinks as a result of increasing temperatures, rising atmospheric CO₂, or as a result of other changes in environmental forcing over the coming decades [3–9].

This uncertainty is linked to ongoing debates regarding the magnitude and spatial consistency of measured increases in tropical forest growth [10,11], and on whether and how tropical forests are changing in their structure and dynamics (e.g. [4,5,7,9,12]). Results from long-term studies of permanent forest plots reported different, and in some cases opposing, trends in tropical forest dynamics. For example, researchers with the Amazon Forest Inventory Network (RAINFOR, [13]) concluded that the growth and productivity of Amazon forests are being stimulated by widespread environmental changes, with significantly increasing turnover rates (i.e. the average rate of biomass growth plus biomass mortality) in almost every region and environmental zone that they have examined over 25 years (1976–2001, [7]). However, in an independent study at La Selva, Costa Rica, researchers found that growth rates decreased in six canopy species during 1984–2000 [12]; and the same trend of decelerating growth was also reported from large forest dynamics plots in Panama and Malaysia [8]. Both these studies found a negative correlation between the annual diameter growth rate of trees and the annual mean of daily minimum temperature, a finding that is at odds with the conclusions of the RAINFOR study, which suggested that increasing temperature may be the underlying cause of accelerating forest dynamics [5].

While many studies have focused on the impacts of increasing temperature and CO₂, the differential responses seen in the above-mentioned studies of tropical forests may be linked to changes in other aspects of climate forcing. In particular, plant growth and productivity in the tropics are thought to be strongly limited by light (solar radiation) as compared to temperature and water availability [14–16]. Since variation in cloud cover occurs at smaller spatial scales, differences in solar radiation forcing could potentially provide an explanation for the observed differences in the trends of tropical forest dynamics in different areas. In this study, we examined changes in tree growth rates at four long-term permanent tropical forest research plots in relation to changes in their solar radiation forcing, in addition to the effects of temperature and precipitation that were examined in aforementioned earlier studies. The objective was to determine the extent to which tropical forests respond to variation in climate forcing and whether this could potentially explain the differing trends in forest dynamics observed in different regions and studies.

2. Methods

(a). Study sites

The study sites were chosen from the Center for Tropical Forest Science (CTFS) network of large-scale forest dynamics plots (FDPs). Four plots that had been censused three or more times were chosen because two or more census intervals were needed to examine changes in growth rates over time (table 1). Barro Colorado Island (BCI) in Panama is covered by lowland moist forest dominated by Bombacaceae and Leguminosae; Huai Kha Khaeng (HKK) in Thailand is a seasonal dry forest dominated by Dipterocarpaceae. Lambir in Malaysian Borneo and Pasoh in Peninsular Malaysia are lowland mixed dipterocarp forests. Both BCI and HKK are semi-evergreen forests with significant and sometimes severe dry seasons, while Lambir and Pasoh are evergreen forests with no or less than one month of dry season [17]. All plots were censused (all trees whose stem diameter at breast height (dbh; approx. 1.3 m) was more than 1 cm were mapped, tagged, identified to species and measured in diameter) at c. five-year intervals using standardized methods [18]. The census years used in this study for each site are listed in table 1.

Table 1.

The four forest dynamics plots (FDPs) used in this study and their site characteristics.^a

site	latitude	longitude	plot area (ha)	census years	elevation (m a.s.l.)	dry seasonb (months)	canopy height (m)	stand densityc (thousand)
Barro Colorado Island, Panama	9°09′ N	79°51′ W	50	1985, 1990, 1995, 2000, 2005	120–160	3	20–40	208
Huai Kha Khaeng Wildlife Sanctuary, Thailand	15°37′ N	99°12′ E	50	1994, 1999, 2004	549–638	6	40–55	113
Lambir Hills National Park, Sarawak, Malaysia	4°10′ N	114°01′ E	52	1992, 1997, 2002, 2007	104–244	0	40–60	362
Pasoh Forest Reserve, Malaysia	2°58′ N	102°18′ E	50	1986, 1990, 1995, 2000, 2005	80–104	1	35	296

^aData from Losos & Leigh [17].

^bDry season length is the number of calendar months with average rainfall <100 mm.

^cStand density is the number of stems larger than 1 cm diameter at breast height, counted in the latest census.

(b). Growth rates

For each census interval, the yearly diameter growth rate (in cm per year) and relative diameter growth rates (in percentage diameter change per year) of each individual tree were calculated for all trees that were alive and greater than 1 cm dbh in the census interval. The absolute and relative changes in diameter of each tree between each of the censuses were divided by the length of the corresponding census interval to obtain yearly absolute and relative growth rates.

Consistent with earlier analyses (e.g. [19]), trees that: (i) grew at a rate greater than 7.5 cm diameter per year; (ii) shrank more than 25% of their initial dbh; (iii) were measured at different heights in two consecutive censuses (usually due to growing buttresses or damaged stems); and (iv) had a main stem that had broken and resprouted, were excluded from the analysis. In other words, this study only included trees that were measured at exactly the same place on the stem in both of the consecutive censuses, and that did not grow or shrink at biologically unrealistic rates (as such cases are usually due to measurement error). In addition, trees with negative growth rates of smaller magnitude than 25% were included, but their growth rates were set to zero.

Figure 1 shows the stand-level mean absolute growth rates (in diameter, cm yr⁻¹) calculated for each census interval at the four sites. As expected, the long-term average growth rates vary among these forests due to differences in their physical environment (e.g. [20]). For the purpose of this study, we controlled for the site-level differences in the baseline (long-term mean) tree growth rates by computing the deviations of growth rates for each census interval from their long-term mean (over the entire census history). For example, the five-year mean growth rate at HKK was 0.23 cm yr⁻¹ during the first census interval (1994–1999), but decreased to 0.21 cm yr⁻¹ during the second census interval (1999–2004). In contrast, at Lambir, the five-year stand-level mean growth rate increased from 0.065 cm to 0.067 cm yr⁻¹ between the two census intervals (1992–1997 and 1997–2002). In terms of direction, these correspond to a decrease of 0.02 cm yr⁻¹ at HKK and an increase of 0.002 cm yr⁻¹ for Lambir.

Figure 1.

(a) Stand-level mean diameter absolute growth and (b) growth deviation at BCI (black), HKK (red), Pasoh (blue), and Lambir (green). Each dashed line represents the mean growth rate over that census interval. The solid lines with horizontal bars show the 95% confidence interval of the mean growth rates.

(c). Climatological data

Since none of the CTFS plots have on-site meteorological stations and it is difficult to evaluate the quality and consistency of data obtained from local meteorological stations, we used monthly climate data from the NOAA/NCEP Climate Prediction Center (http://iridl.ldeo.columbia.edu/docfind/databrief/cat-atmos.html). Specifically, for precipitation, average annual precipitation (mm yr⁻¹) for each census period was calculated from the product PREC/L (Precipitation REConstruction over Land, [21]) by summing the raw monthly data and dividing by the census interval. Maximum Climatological Water Deficit (MCWD) values were also computed from the precipitation measurement data. MCWD is defined as the most negative value of climatological water deficit attained over a year, calculated from the difference between precipitation and evapotranspiration, MCWD is another metric of moisture availability that provides a simple measure of drought stress [22,23]. In a similar manner, monthly mean daily minimum, maximum and mean temperatures (°C) were obtained from the EVE climate product [24], and then averaged to yearly mean values for each of these temperature measures.

Estimates of the solar radiation forcing at each site during each census interval were obtained from the satellite-based radiation measurements of the International Satellite Cloud Climatology Project (ISCCP, http://isccp.giss.nasa.gov/, data available from July 1983 to June 2008). The shortwave downwelling flux at surface (W m⁻²) at each site was prescribed from the ISCCP-FD RadFlux dataset [25] using the latitude and longitude of each site to locate the nearest land grid cell, and averaging the original three-hourly data for each of the census intervals.

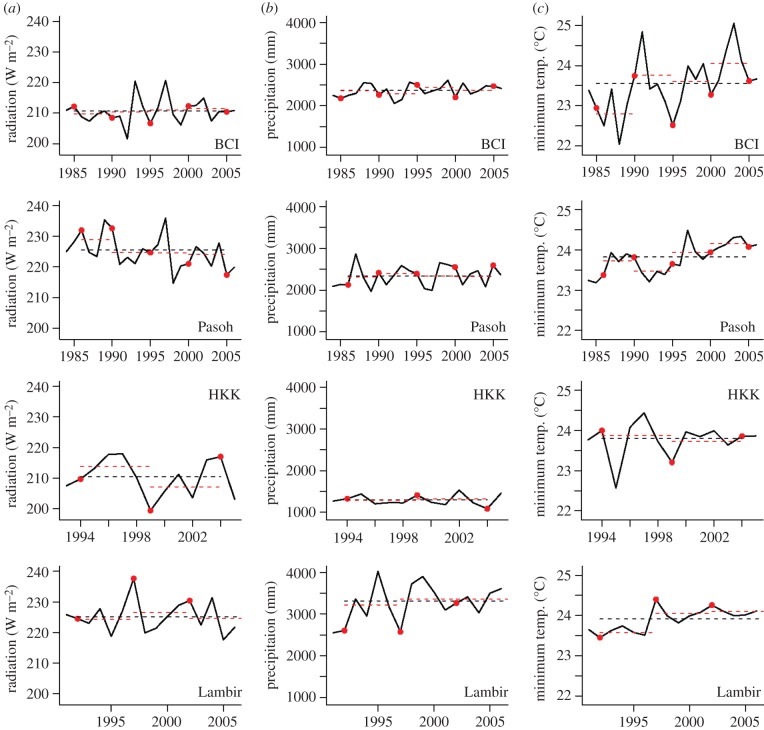
Mean values of all the above climate variables were calculated for each census interval (from July of the year of one census to June of the year of the next census) for each site, and compared with the local means over the entire period when the forests were monitored (from July of the year of the first census to June of the year of the last census; figure 2). The long-term local means of the climate variables at each site differ significantly from one another. For similar reasons to growth, we computed deviations of the climate variables from their long-term means at each site. This approach has advantages when, as here, the available climate data had not been collected locally at each site since regional data are likely to be different from the local climate conditions. This is particularly true for sites such as HKK, which are mountainous: while its higher elevation means that the HKK temperature is on average lower than the regional estimate by about 4°C, its temporal pattern of variability is likely to parallel that of surrounding areas.

Figure 2.

(a) Changes in annual mean incoming solar radiation, (b) annual total precipitation, and (c) daily minimum temperature at each site. The annual values are calculated from July of one year to June of the next. See §2 for details and data sources. The grey dots indicate the time of each census taken place at each site. The red dashed lines are the mean over each census interval, while the black dashed lines are the mean over the entire study period. The distances between each red dashed line to the black dashed line are the deviations used in the analysis (see §2).

3. Results

Both absolute growth rates (in cm diameter) and relative growth rates were analyzed in this study. Since relative growth rates displayed near-identical trends throughout the analyses, only the results using absolute growth rates are presented here. The deviations of inter-census growth rates from the mean for the entire study period were plotted against the climate deviations of the same time period. In all cases, the regression models fitted to the growth measurements took into account differences in variances and sample sizes of different sites and census intervals.

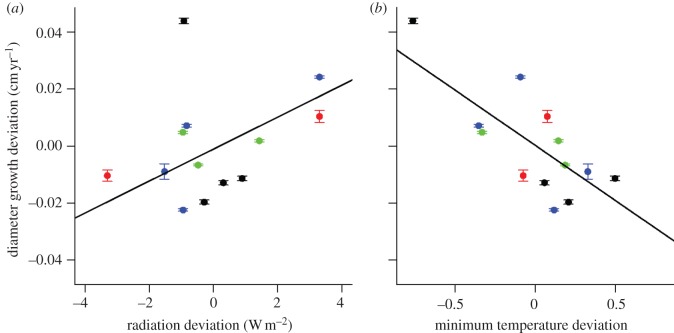
A single factor regression analysis encompassing all stems measured in the censuses showed that variations in stand-level growth rates (cm diameter per year) were positively correlated with incoming solar radiation (R² = 0.31, p = 0.05, figure 3a). When only the three Asian sites (HKK, Pasoh, Lambir)—where there had been greater directional changes in solar radiation—were examined, the relationship was even more statistically significant (R² = 0.54, p = 0.02). The magnitude of the effect was the greatest at Pasoh, where the absolute growth rate dropped by 0.01 cm yr⁻¹ per watts m⁻² of decrease in incoming solar radiation over the census intervals. At HKK and Lambir, the ΔG/ΔR ratios (unit change of growth rate per unit change of radiation) were 0.003 and 0.005 (cm yr⁻¹ per watt m⁻²), respectively.

Figure 3.

(a) Stand-level mean diameter absolute growth (cm yr⁻¹) deviation in relation to solar radiation and (b) daily minimum temperature deviations at BCI (black), HKK (red), Pasoh (blue) and Lambir (green). The solid lines with horizontal bars show the 95% CI of the mean growth rates. Note that the black-colored data point at the top of each plot is the exceptionally high growth rate observed between censuses 1985 and 1990 at BCI. The removal of this data point enhances the statistical significance of the positive relationship between growth and solar radiation, but reduces the statistical significance of the negative relationship between growth and temperature (see §3).

Total annual precipitation was negatively correlated with solar radiation at the three Asian sites, but not at BCI (see electronic supplementary material, table S1). There was no negative relationship between stand-level tree growth rates and total precipitation either across all sites (R² = 0.03, p = 0.58; see electronic supplementary material, figure S1a), or within the Asian sites (R² = 0.07, p = 0.49). There was also no significant relationship between stand-level growth rates and maximum climatological water deficit (MCWD), either across all sites (R² = 0.04, p = 0.49; see electronic supplementary material, figure S1b), or within the Asian sites (R² = 0.33, p = 0.10). Therefore, the observed changes in tree growth rates appear to be more strongly influenced by solar radiation (light) than by moisture availability, as measured by either precipitation or MCWD.

A significant negative relationship was also found between stand-level tree growth rates and daily minimum temperature (R² = 0.40, p = 0.02; figure 3b). However, the statistical significance of this relationship was strongly influenced by the single point of high growth rate at BCI during the period 1985–1990 (R² = 0.29, p = 0.07 when this census interval is taken out).

When the meteorological variables were inserted into a multiple regression model, the effects of incoming solar radiation and minimum temperature identified in the above univariate regression analyses increased in significance (table 2): stand-level tree growth rates were positively correlated with solar radiation, and negatively correlated with daily minimum temperature (R² = 0.85, p < 0.001; figure 4). These effects appear to be independent. As can be seen in the figure, variation in tree growth rates across the sites and census periods can be largely explained by a combination of variation in solar radiation and daily minimum temperatures. For example, the high stand-level growth rate that occurred at BCI between censuses 1985 and 1990 despite typical radiation levels during that period (figure 2) is explained by the lower daily minimum temperatures during that period. Similarly, the unexplained increase in tree growth rates that occurred at HKK as temperature increased (red points in figure 3b) is explained by a concurrent increase in solar radiation between the two census intervals. There was no evidence for an interaction between the effects of radiation and temperature responses (p = 0.44). Analysis of the residuals indicates no clear trends in the distribution of the observations around the fitted multiple regression model (see electronic supplementary material, figure S2), indicating that the effects of temperature and radiation are reasonably approximated as independent linear effects.

Table 2.

Multiple regression analyses of tree growth rates in relation to climate variables for all trees and stratified by size class.

	all trees		small (<20 cm)		medium (20–50 cm)		large (≥50 cm)
	coefficient	s.e.	coefficient	s.e.	coefficient	s.e.	coefficient	s.e.
solar radiation	0.00679	0.00123	0.00731	0.00129	−0.00056	0.00426	−0.01404	0.01124
minimum temperature	−0.04540	0.00754	−0.04600	0.00735	−0.06323	0.03326	−0.06093	0.09025
R2	0.85		0.86		0.28		0.2
model p-value	7.1 × 10−5		5.9 × 10−5		0.19		0.31

Figure 4.

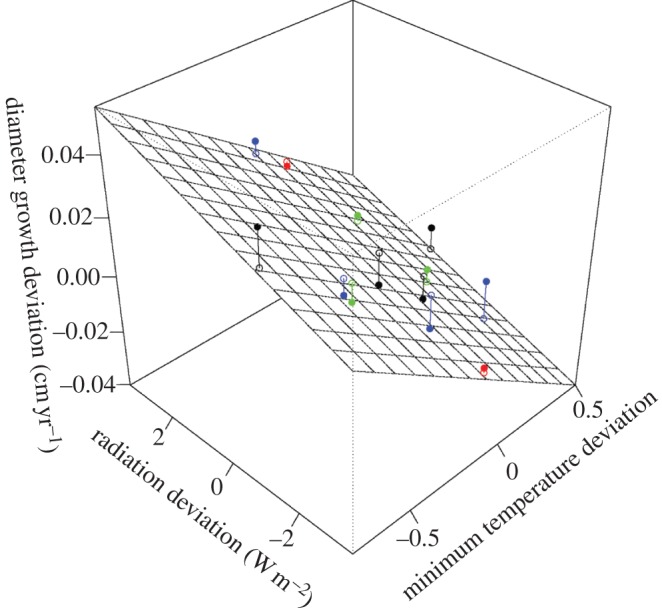
Stand-level mean diameter absolute growth deviation (cm yr⁻¹) in relation to solar radiation and daily minimum temperature deviations at BCI (black), HKK (red), Pasoh (blue) and Lambir (green). The solid points are the observed data points and the open points are their projections on the plane fitted in multiple linear regression. The residuals of the observations around the fitted relationship are shown in the electronic supplementary material, Figure S3.

To better understand the nature of these stand-level responses to long-term climate variability in more detail, we examined the distribution of the stand-level response. Histograms of the growth deviations of individual trees at each site for all census intervals illustrate how the trends in mean stand-level growth rates arise from the responses of individual trees (see electronic supplementary material, figure S3). For example, at HKK (see electronic supplementary material, figure S3c) the distribution was right-skewed (i.e. more individuals with increased growth rates, skewness = 2.91) over the period 1994–1999, while the later census interval 1999–2004 had a left-skewed (skewness = −2.91) distribution of relative growth deviation (i.e. more individuals with decreased growth rates). The two distributions are significantly different from each other as shown by Kolmogorov-Smirnov test (D = 0.4251, p < 0.001). Thus the increased stand-level mean growth rates were not the result of the exceptional performance of just a few individuals, but rather a systematic shift in growth rates of large numbers of individuals during this census period.

We repeated our climate regression analyses separately for three different tree size classes: trees with diameters (dbh) less than 20 cm, those with diameters between 20–50 cm dbh and those with diameters greater than 50 cm (see table 2 and electronic supplementary material, table S2). These analyses show that the stand-level responses to radiation and temperature variability seen in figures 2 and 3 primarily reflect the response of trees less than 20 cm in diameter. Specifically, the smallest size-class exhibits the positive relationship between growth rate and solar radiation (R² = 0.3, p < 0.05) and the negative relationship between daytime minimum temperatures and tree growth rate (R² = 0.4, p < 0.02), with both the relationships being of similar magnitude to the corresponding relationships in stand-level regression. Similarly, no significant relationships were found between growth rate of the small trees and either precipitation or MCWD (see electronic supplementary material, table S2). Moreover, as for the stand-level analysis, when combined into a single multiple regression model, the strength of both the solar radiation and temperature relationship increased (table 2, R² = 0.86, p < 0.001). In contrast, no significant correlations were found for any of the radiation, temperature and moisture-related climate variables for either the medium (20–50 cm) or large (>50 cm) size classes (see table 2 and electronic supplementary material, table S2). Although the effects of temperature and radiation for the medium and large tree size classes were not statistically significant (i.e. the regression coefficients were not significantly different from zero), the confidence bounds for the fitted relationships also indicate that they are not significantly different from the effects of temperature and radiation estimated using stems in all size classes (see electronic supplementary material, figure S4).

4. Discussion

This study showed positive relationships between stand-level tree growth rates and solar radiation (figure 3a) and a negative relationship between growth rates and daily minimum temperature across four tropical forest sites (figure 3b). There was no significant correlation between stand-level growth rates and precipitation or MCWD (see electronic supplementary material, figure S1). When examined as single factors, incoming solar radiation and temperature variability each explain significant components of the observed variability in long-term tree growth rates across the sites. While the effect of radiation on growth rates appears to be consistently positive across all sites, growth rate variation at HKK did not respond negatively to temperature and the growth–temperature relationship is weakened when the extreme high value of growth between censuses 1985 and 1990 at BCI is removed (figure 3b).

The results of the multiple linear regression (figure 4) indicate that most of the unexplained variability in the univariate radiation and temperature relationships plotted in figure 3a,b can be attributed to concurrent changes in the other meteorological variable. For example, the observed growth rate change that occurred in BCI between 1985 and 1990 in the absence of any significant change in incoming radiation levels (the black outlier point in figure 3a) is accounted for by the concurrent decrease in the daytime minimum temperature that occurred during the period. Similarly, the decrease in growth rates between the 1994–1999 and 1999–2004 HKK censuses, which occurred despite near identical daytime minimum temperatures (see red points in figure 3b), is explained by a concurrent increase in incoming radiation levels between the two census periods. As the results of the multiple regression indicate, the effects of variability in solar radiation and daily minimum temperature on tree growth appear to be largely independent and, considered together, explain most of observed variability in long-term tree growth rates across the four sites (figure 4).

Our results regarding the importance of radiation as a significant driver of variability in tree growth rates accord with the suggestions of an earlier study [26], which hypothesized that observed unexplained inter-annual variability in tree growth rates at La Selva, Costa Rica may be arising from variation in incoming solar radiation levels. The results of this analysis build upon the Clark and Clark [26] study in several important respects. First, it provides, as far as we are aware, the first clear demonstration of a relationship between long-term, stand-level variability in growth rates and incoming solar radiation levels across a series of tropical forest sites (figure 3a). Second, it indicates that the positive growth response to increases solar radiation variability (figure 3a) is a distinct and orthogonal response to the observed negative effects of increasing minimum temperature seen in this study (figure 3b) and in the earlier studies of Clark et al. [12] and Feeley et al. [8].

The results of this study also suggest a potential explanation for the differing results obtained in earlier studies of the response of tropical forests to climate change. As noted in §1, Amazon forests have been observed to be experiencing accelerated dynamics over the past several decades, including significantly increased rates of tree growth and mortality, recruitment rates and above-ground biomass [5,7,10]. However, a separate study conducted at BCI, Panama did not show the same trends [27]; decreasing growth rates were also reported both at BCI and Pasoh (Malaysia) during a time period overlapping the above-mentioned studies conducted in the Amazon [8], and a similar deceleration was also observed in a Costa Rican tropical forest [12].

Whereas the above studies focused on changing temperature and atmospheric CO₂ concentrations as explanatory factors for observed trends in tropical forest dynamics, the results of this analysis indicate that solar radiation variability is also an important aspect of environmental forcing affecting the dynamics of tropical tree growth. In contrast to the more spatially uniform trends in atmospheric CO₂ and temperature, as seen in figure 2, the four tropical sites analyzed in this study have experienced different trends and magnitudes of changes in solar radiation forcing over the past few decades, giving rise to spatially variable trends in patterns of tree growth rates. This conclusion is consistent with Nemani et al.'s [15] analysis, which indicated that plant growth in the tropics is significantly limited by radiation availability, and that different tropical regions have experienced differing trends in solar radiation variation over the 1980s and 1990s.This pattern, together with the results of this study, suggests that spatial and temporal variation in solar radiation, in conjunction with temperature, provide a consistent explanation for the apparently conflicting results arising from the Amazon-based RAINFOR network of plots [5,7,10], compared to those obtained at analyses at BCI and La Selva and Pasoh [8,12,27].

The results of the size-stratified analyses (see table 2 and electronic supplementary material, table S2) and analysis of growth distributions (see electronic supplementary material, figure S3) indicate that the stand-level responses to radiation and temperature seen in figures 3 and 4 reflect systematic changes in the distribution of tree growth rates, particularly among trees of less than 20 cm in size. This is not surprising since, at all the sites, the majority of stems (between 88–96%, depending on the location) are in the smallest size class. When the responses of larger-diameter trees in the medium and large size classes are examined separately, neither shows significant relationships with any of the meteorological variables considered. While the absence of a positive response to radiation among larger-sized trees could be explained by their growth not being light-limited (since larger trees are generally well-illuminated), it is less obvious why large trees should not experience negative effects of increasing temperature. The environmental responses of large trees could be more heterogeneous than those of smaller trees. However, it is also important to note that while the estimated relationships for the medium and large size classes are not significantly different from zero, they are also not significantly different from the temperature and radiation trends estimated using stems in all size classes (see electronic supplementary material, figure S4). A key factor here is that the sample sizes for the medium and large size classes are substantially smaller than for the smaller tree size class, which decreases the ability to detect effects in heterogeneous populations: for example, at Lambir, the medium and large classes were comprised of 9732 and 1994 stems, respectively, compared to 326 717 stems in the small size class. Distinguishing between the above explanations will require a stratified sampling approach in order to ensure that sufficiently large sample sizes are obtained across the tree size spectrum.

Our analyses did not reveal any statistically significant associations between variability in long-term growth rates and precipitation or MCWD variability. This result accords with the findings of Clark and Clark [26], who found no relation between annual rainfall and growth rates at the La Selva tropical forest in Costa Rica. Our findings are also consistent with Phillips et al. [28], who concluded that drought impacts on Amazon tropical forests are primarily mediated by tree mortality rather than rates of tree growth (see also [29]). Effects of precipitation on tree growth rates have been found in seasonal tropical forests, however, where analyses have frequently found significant correlations between either seasonal or annual precipitation and tree ring widths (e.g. [30,31]). Two of the four plots in this study (HKK and BCI) are seasonal forests with significant dry seasons (table 1) and have a partially deciduous canopy. Since most of the annual net growth observed is gained during the wet season (Ashton 2011, personal communication), we examined the correlation between growth variation and changes in mean wet season monthly precipitation (i.e. months with >100 mm rainfall), but we did not find any significant positive relationship (R² = 0.29, p = 0.27 for HKK and BCI).

The magnitudes of the variation in long-term tree growth rates documented in this study appear to be relatively modest: the largest detected variation in mean diameter growth rate, found at the BCI plot, was only 0.06 cm yr⁻¹ (figure 1). However, it is important to realize that this growth rate variation was associated with only 1.81 watts m⁻² variation in the level of solar radiation forcing between census periods—equivalent to only 0.86% of the average annual solar radiation. However, as figure 2 illustrates, the five-year census intervals average over substantial amounts of inter-annual variability in climate forcing. The yearly average radiation deviations at BCI range from −9.04 watts m⁻² in 1992 to +10.06 watts m⁻² in 1997, while the five-year-census-interval average radiation deviations only range between −0.92 watts m⁻² and +0.90 watts m⁻²; and the mean absolute deviation of yearly average radiation is 3.06 watts m⁻², versus 0.60 watts m⁻² for census intervals. Similar patterns occur at all sites, where both the year-to-year range of radiation variation and the year-to-year mean absolute deviations are substantially larger compared to those between census intervals (Pasoh: 10.40 ∼+ 10.80 watts m⁻² versus −1.53 ∼+ 3.31 watts m⁻² and 4.39 watts m⁻² versus 1.65 watts m⁻²; Lambir: −7.58 ∼+ 12.45 watts m⁻² versus −0.95 ∼+ 1.43 watts m⁻² and 4.28 watts m⁻² versus 0.95 watts m⁻²; HKK: −11.06 ∼+ 7.49 watt m⁻² versus −3.30 ∼+ 3.30 watts m⁻² and 4.91 watts m⁻² versus 3.30 watts m⁻²). Thus, compared to the levels of solar radiation variability seen between 5-year censuses, all sites have greater than 3-fold increases in the level of variability of solar radiation forcing at the inter-annual timescale. Given this, it seems likely that the five-year average growth rates measured by the current tree censuses mask significant shorter-term variation in tree growth rates in response to inter-annual solar radiation variability within census periods. Given the responses to small changes in five-year average solar radiation detected in this study, we anticipate that inter- and intra-annual growth rates will vary substantially in response to the higher order of magnitude variability in solar radiation that occurs at annual to sub-annual timescales.

CTFS has recently begun a new measurement program to quantify inter- and intra-annual variation in forest dynamics at the above-mentioned sites, as well as additional sites within the CTFS network (http://www.ctfs.si.edu/group/Carbon/Sites). These measurements will enable examination of the relationship between tree growth rates and environmental variability at these shorter time scales. In addition, new meteorological stations are in the process of being deployed at several of the CTFS plots (http://www.ctfs.si.edu/group/Carbon/) that will provide more accurate measures of the environmental conditions at each site than current estimates, which are based on measurements at surrounding locations. Given the positive relationships between the five-year stand-level mean growth rate and solar radiation identified in this study, we anticipate a strong signature of solar radiation forcing in inter- and intra-annual growth rates. The newly initiated more frequent growth sampling regime will be helpful particularly for those sites with shorter census histories, such as HKK. Only two census intervals were available for this site, and so currently it is only possible to test for monotonic trends of growth rates in relation to climate change, despite clear evidence from the climate measurements that the climate variables did not simply either increase or decrease over the 10-year period. As figure 2 illustrates, there are typically larger inter-annual variations in both directions than the change between the census intervals and having more frequent measurements of tree growth at these sites will significantly increase the statistical power of tests to quantify how changes in meteorological forcing affect tree demographic rates in different tropical forest formations [32]. These short-term measurements will be particularly powerful when combined with the less-frequent, longer-term census information used in this study, because it will facilitate understanding of how effects of short-term climate variability on tree demography translate into effects on longer timescales.