Phase plane based identification of fetal heart rate patterns

Abstract

Using a phase plane analysis (PPA) of the spatial spread of trajectories of the fetal heart rate and its time-derivative we characterize the fetal heart rate patterns (fHRP) as defined by Nijhuis. For this purpose, we collect 22 fetal magnetocardiogram using a 151 SQUID system from 22 low-risk fetuses in gestational ages ranging from 30 to 37 weeks. Each study lasted for 30 minutes. After the attenuation of the maternal cardiac signals, we identify the R waves using an adaptive Hilbert transform approach and calculate the fetal heart rate. On these datasets, we apply the proposed approach and the traditionally used approaches such as standard deviation of the normal to normal intervals (SDNN) and root mean square of the successive difference (RMSSD). Heart rate patterns are scored by an expert using Nijhuis criteria and revealed A, B, and D patterns. A receiver operator characteristic (ROC) curve is used to assess the performance of the metric to differentiate the different patterns. Results showed that only PPA was able to differentiate all pairs of fHRP with high performance.

I. Introduction

The evaluation of fetal heart rate patterns (fHRP) can provide clinicians with valuable information regarding the fetus health during pregnancy. One of the key features of the fHR is the expression of sleep-wake cycles. Using ultrasound studies, Nijhuis has classified fetal heart rate (fHR) into four different patterns, A, B, C, and D. FHRP are recognized by baseline frequency and variability, and the fetal heart rate (fHR) accelerations and decelerations in a stable time frame of at least three minutes [1]. Pattern A is characterized by a stable heart rate with occasional accelerations/decelerations with small oscillation bandwidth of less than 5 beats per minute (bpm). Pattern C is characterized by a stable heart rate with no accelerations with oscillation bandwidth slightly greater than 5 bpm. Pattern B is characterized by a varying heart rate with frequent acceleration/decelerations with wider oscillation bandwidth greater than 5 bpm. Pattern D is characterized by frequent long lasting and large accelerations from the baseline with a wider oscillation bandwidth of greater 10 bpm.

Kariniemi et al. reported the first fetal magnetocardiogram (fMCG) using a super conducting quantum interference device (SQUID) [2]. SQUID systems are non-invasive and have excellent signal to noise characteristics compared to fetal electrocardiogram (fECG) recordings taken from the mother’s abdomen, especially after the 24th week of gestation when the fECG is not easily detectable and, SQUID systems also have high temporal resolution (<1ms). Multi-sensor SQUID arrays have been used for fMCG detection [3]. Compared to a single channel SQUID system, an array has the advantage of covering a large area simultaneously and offers the possibility of improved signal-to-noise ratio by combining the fMCG detected from several channels. One difficulty for the researcher interested in studying the fHR using SQUID technology is that the healthy fetus may move during the recording period which in turn may result in significant changes in the amplitude or morphology of the fMCG waveform [4]. Because a healthy fetus may become active, the algorithms developed to extract the timing of R waves from the typical adult ECG may have high error rates when applied to either fMCG or fECG data. Utilizing fMCG obtained from spatially dense SQUID array system, novel approaches based on Hilbert transform have been introduced to reliably identify the fetal R-wave [5, 6].

FHRP is one of the confounders in the quantification of the heart rate variability using measures such as standard deviation of normal to normal intervals (SDNN), root mean square of successive differences (RMSSD), and power spectral analysis. SDNN captures the long-term variability and hence quantifies low frequency component of the heart rate while RMSSD captures the short-term variability and hence quantifies high frequency components of the heart rate. Since fHR show important dynamical properties of the heart that may help to delineate healthy from sick fetuses, it is important to study them as a function of the heart rate patterns. The traditional fHR analyses performed on the whole heart rate tracings are now applied to the classified fHR patterns to better understand the fetal maturation [7, 8]. To date, fHRP is obtained by manual scoring and is a laborious process and further it involves high degree of subjectivity. As a first step towards the objective of automated scoring of the fHRP, we propose a phase plane analysis (PPA). We compare its performance with traditionally used measures such as SDNN and RMSSD.

II. Materials AND Methods

A. Materials

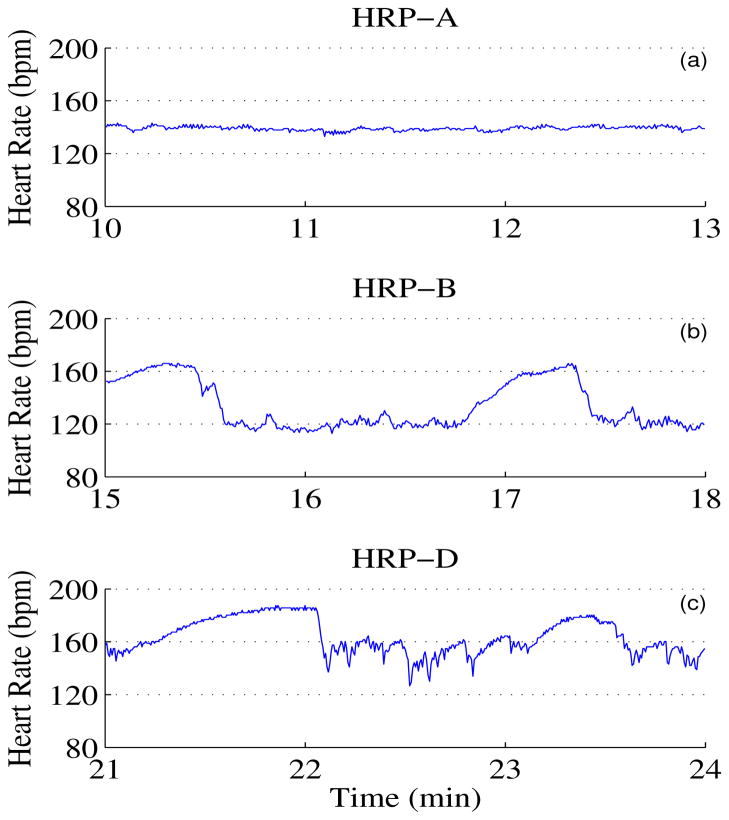
We obtain 22 fMCG datasets using a 151 SQUID array system from 22 pregnant women that gave birth to healthy neonate at term. The sample frequency is 312.5 Hz. The gestational age of these fetuses varied between 30 and 37 weeks. Many important developments take place during third trimester. For example, lung maturation and development of sleepcenters are shown to develop between 30 weeks and term. Thus any abnormalities that can happen in this time period can be captured if we have a good benchmark data. In addition, the expression of sleep-wake cycles in fHRP and their evolution gives an insight in the fetal neurological maturation [1]. Hence this time period is used to study the fetal heart rate patterns. The data is bandpass filtered between 0.5 to 50 Hz using Butterworth filter with zero phase distortion. We attenuate the maternal cardiac signals using signal space projection technique [9] and identify the fetal R-wave using an adaptive Hilbert transform approach [5, 6]. One of the dataset was discarded because of the improper identification of the fetal R wave. Heart rate was quantified as beats per minute, bpm. These heart rates were scored for the fHRP using Nijhuis definition (see Introduction) by visual inspection. In this analysis we discarded data that are either spurious beats or that formed parts of the transition from one pattern to another. Further, pattern C was found in less than 2% of data, and hence this was discarded from the further analysis. There are 117 three minute windows of pattern A, 51 three minute windows of B and 6 three minute windows of pattern D. Fig. 1 shows representative examples of patterns A, B and D. We compute the heart rate variability parameters such as SDNN, RMSSD, and the PPA metric in disjoint three minute windows. For this purpose we use only three minute windows in which the patterns remained stable.

Fig. 1.

Fetal Heart Rate Patterns. (a)–(c) represents HRP A, B and D respectively.

B. Need for the new approach

One of the standard techniques used in the literature to characterize fetal heart rate is Poincaré map analysis which is a plot of (n+1)^th beat versus n^th beat. Concept of Poincaré analysis is used in nonlinear dynamical system analysis to characterize the recurrence property of the trajectories in the phase space. In the case of heart rate analysis, though this concept is borrowed from the nonlinear dynamical system theory with the objective of characterizing the nonlinear properties of the heart rate, the characterization of the map usually involved computing the linear measures such as SDNN and RMSSD. Thus, the complete characterization of the nonlinear representation of the heart rate via the Poincaré map has not been done before [10]. In earlier study [11], nonlinear dynamical indices have been applied to the heart rate of low-risk and Intrauterine Growth Restricted (IUGR) fetuses. This study demonstrated that the correlation dimension of the RR intervals of low-risk fetuses increases as a function of gestation age, where IUGR fetuses do not show such an increase. However, analysis are done on the delay coordinates and not on the Poincaré map. To fill this gap we introduce a novel method to quantify the fetal heart rate which involves computing the fill factor of the trajectories of the heart rate and its first time derivative in the space which is traditionally called phase plane plot. Instead of plotting the current value and its immediate time neighbor in the phase space, we plot the heart rate and its time derivative. This is to avoid the influence of the autocorrelation of the heart rate in quantifying the PPA. Instead of the immediate neighbor in time, a delayed value can also be plotted versus the current value as done in the reconstruction of the attractor from the single time series using Taken’s theorem [12]. However, the optimal delay value that can minimize the autocorrelation of the heart rate may not be computable here because of the power-law correlations in the heart rate [13]. Hence we plot the heart rate and its first time derivative and quantify phase plane by computing the fill factor, namely the area occupied by the trajectories. In this work we use this approach to characterize the fHRP and study its performance in distinguishing different fHRP.

C. Method

We denote the time marker of the j^th R wave as τ_j and define heart rate hr_j at this point as 60/(τ_j − τ_j−1) where the unit of τ is in seconds. We define the first time derivative ( ${hr}_j^{\prime }$) of the heart rate as (hr_j+1 − hr_j−1)/( τ_j+1 − τ_j−1). A plot of ${hr}_j^{\prime }$ versus hr_j will yield the phase plane plot. In contrast to the random scenario which will occupy the entire space, the trajectories of the heart rate and its derivative will be confined to a small subspace owing to the fractal nature of the heart rate [13] and we quantify this property by computing the area occupied by the trajectories.

To compute the area we use the Monte-Carlo approach. In this approach we populate the phase plane with uniformly distributed random numbers and calculate the probability (P ) of the random number that fall on the trajectories of the heart rate and its time derivative. The probability P multiplied by the range of the heart rate and the range of ${hr}_j^{\prime }$ will provide the area occupied by the trajectories. We will also compute SDNN and RMSSD of the heart rate and compare their performances in distinguishing the different heart rate patterns. SDNN is computed by calculating the standard deviation of the heart rate. RMSSD is computed by calculating the standard deviation of the successive difference of the heart rate.

$$\mathit{SDNN}=\sqrt{\frac{1}{N-1}\sum _{j=1}^N{({hr}_j-\overline{{hr}_j})}^2}$$ (1)

$$\mathit{RMSSD}=\sqrt{\frac{1}{N-1}\sum _{j=1}^{N-1}{({hr}_j-{hr}_{j-1})}^2}$$ (2)

To compare the performance of the metric in separating the three FHPRs namely A, B and D we use Receiver Operating Characteristic (ROC) curve which is a plot of sensitivity and 1-specificity. The area under the ROC curve (AUC) gives the degree of separation between the two groups.

III. Results And Discussions

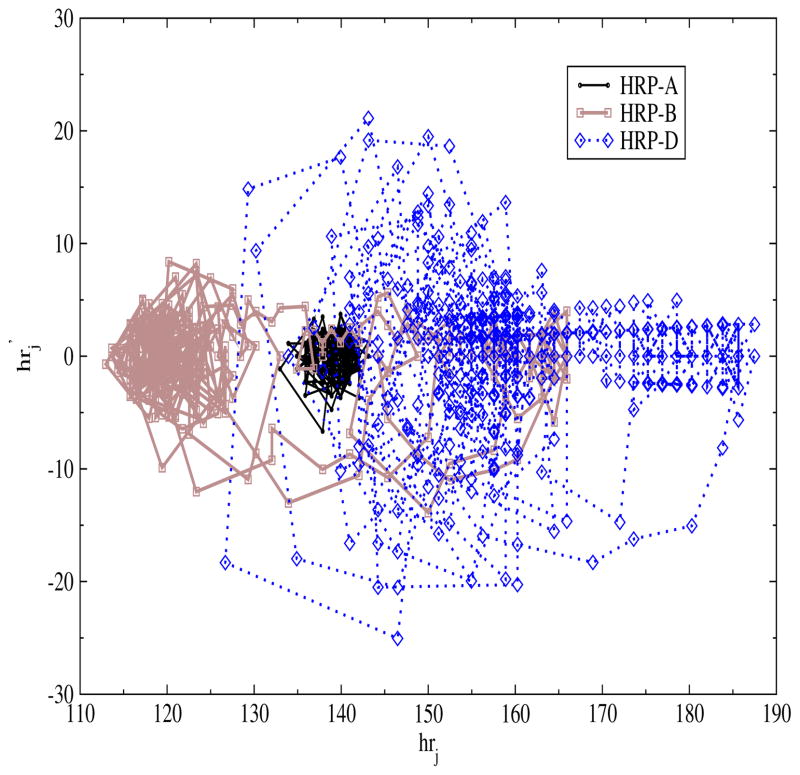
In Fig. 2, we show the phase plane plot of the three different heart rate patterns namely A, B and D (shown in Fig. 1). Qualitatively one can infer from Fig. 2 that the trajectories of pattern D span to a larger area and that of pattern A are confined to a smaller region of the space while for pattern B the extent of spread lies in between that of patterns A and D. In the next step we quantify these patterns by calculating the area of the phase plane.

Fig. 2.

Phase plane plot of heart rate and its first time derivative for three different heart rate patterns namely A, B and D.

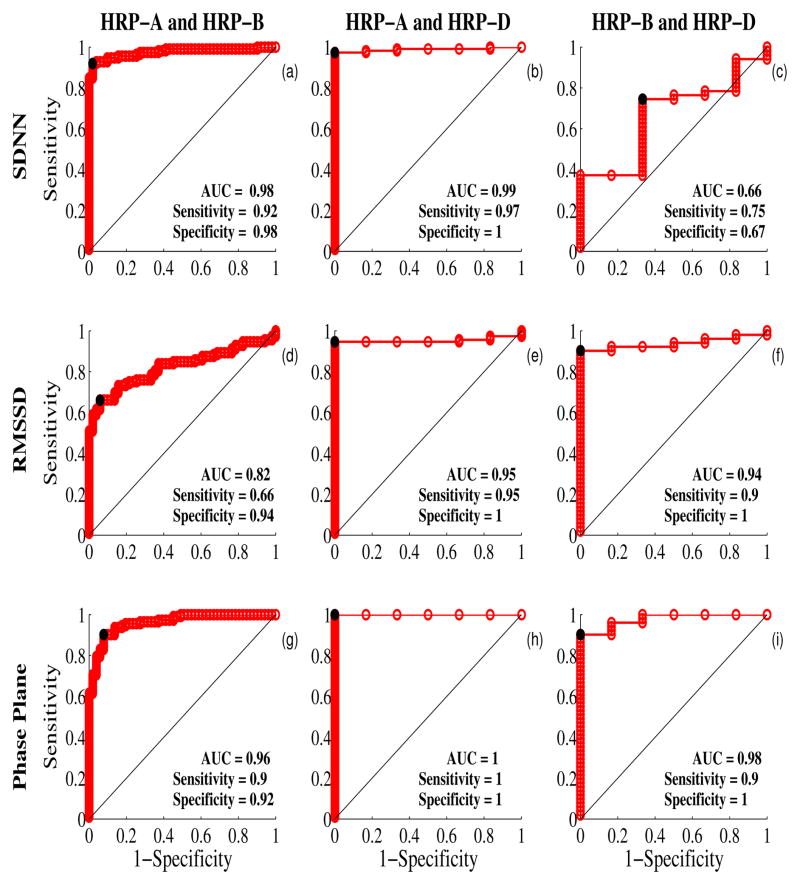
The ROC curves computed for SDNN, RMSSD, and the area of the trajectories in the phase plane are shown in Fig. 3. As mentioned above we use the AUC as the performance measure. Between patterns A and B, SDNN is able to distinguish them better than other measures (see Fig. 3(a, d, g)). Between patterns A and D, PPA performs (Fig. 3h) the best followed by SDNN (Fig. 3b) and RMSSD (Fig. 3e). Between patterns A and D, again PPA (Fig. 3i) performs the best followed by RMSSD (Fig. 3j) and SDNN (Fig. 3c). Overall only PPA is able to separate the different states with high performance.

Fig. 3.

Assessment of the performances of the three metrics namely, SDNN, RMSSD and area of the phase plane. (a)-(c) represent the comparison between different groups using SDNN. (d)-(f) represent the comparison between different groups using RMSSD and (g)-(i) represent the comparison between different groups using area of the phase plane. The area under the ROC curve (AUC) is given in the inset. The diagonal line represents the null hypothesis that there is no difference between the two groups. The knee point (sensitivity and specificity) that best separates the two groups is also given in the inset and is shown in black dot in the curve.

In this work the fHR is characterized using two linear measures, namely SDNN and RMSSD and a nonlinear measure namely the area spanned by the trajectories of heart rate and its first time derivative. As the pattern A differs from patterns B and D mainly in the variation of the heart rate, the linear measure SDNN is able to distinguish between A and B and between A and D. While the patterns B, D show almost same degree of variation, SDNN is not able to distinguish these two patterns clearly. On the other hand PPA quantifies the interaction between the low and high frequency terms and was able to distinguish patterns B and D when compared to the linear measures. The performance of the RMSSD is in between the performance of the other two metrics in the comparison of patterns between A and B and between A and D. While it separates better the patterns between B and D compared to SDNN.

SDNN and RMSSD are linear measures as they quantify the linear properties of the heart rate while the area of the phase plane quantifies the nonlinear property of the heart rate. SDNN quantifies the long range correlations (low frequency component) in the heart rate while RMSSD quantifies the short range correlations (high frequency component) in the heart rate. Phase plane plot from the way it is defined it quantifies the interaction between the low and high frequency components. Further, this interaction is quantified in terms of the fill factor which is similar to the joint probability distribution and hence it represents nonlinear property of the heart rate.

In general nonlinear dynamical indices perform better in characterizing a signal compared to the linear indices. The starting point for the application of the nonlinear dynamical index to a signal is the representation of the one dimensional signal in a multidimensional phase space. This is accomplished using the delayed coordinates with delay representing the decorrelation time [12]. Thus, the multidimensional projection, by virtue of its construction, already provides characterization of the interaction between multiple autocorrelation function which is equivalent to the higher order correlations and makes the quantification nonlinear. Further, the topological property (the spatial organization and recurrence nature) of the trajectories adds flavor to the nonlinear dynamical indices which cannot be obtained in any of the time domain analysis. Because of these reasons the nonlinear dynamical indices perform better than the linear measures.

IV. Conclusion

In this work the nonlinear measure is able to distinguish all the patterns clearly. In future work, we will perform linear discriminant analysis to improve the performance of the PPA by combining with the SDNN and/or RMSSD analysis. Further, we will also explore the quantification of sympathovagal balance using the PPA.