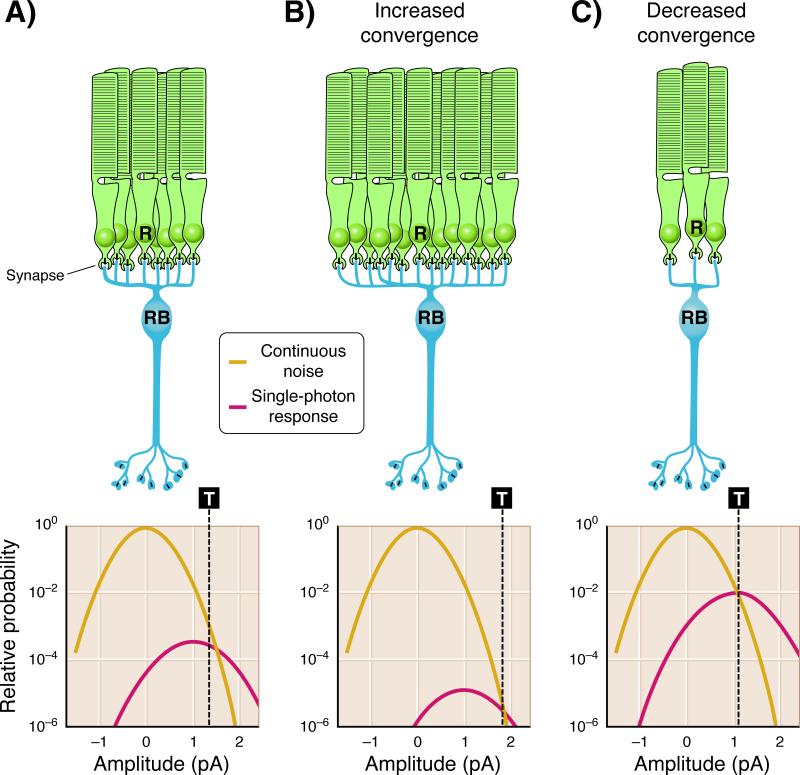
Figure 4.

Optimal position of the threshold in rod bipolar cells is dependent on convergence. The extent of convergence of rods onto rod bipolar cells will alter the optimal position of the threshold (T - dashed line) that separates single-photon responses from continuous noise. A: In the mouse retina ~ 20 rods converge on downstream rod bipolar cells [49]. The task for rod bipolar cells is to distinguish single-photon responses (Gaussian distribution with mean amplitude ~ 1 pA) from the rod continuous noise (Gaussian distribution with mean amplitude ~ 0 pA). Previous studies have shown that the optimal position of the threshold (T ~ 1.3 pA) is close to the crossing point between these Gaussian distributions [40, 50]. Events larger than threshold are more likely single-photon responses and are preserved, while those smaller than threshold are more likely noise and are discarded. B: The optimal position of the threshold will change with the extent of rod convergence onto rod bipolar cells. As convergence increases, the probability of observing continuous noise increases with respect to the probability of observing single-photon responses, since near visual threshold a small minority of the rods receive a photon. Consequently the threshold would need to be positioned at higher amplitudes (T ~ 2 pA) to allow the optimal separation of single-photon responses from continuous noise. C: As convergence decreases, the probability of observing single-photon responses increases with respect to the probability of observing continuous noise, requiring the threshold to be positioned at a lower amplitude (T ~ 1 pA) to allow the optimal separation of single-photon responses from continuous noise. Adapted from [23].