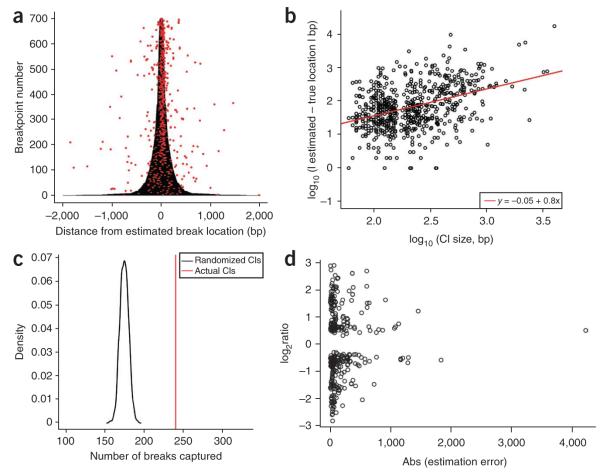
Figure 2.

Confidence intervals. (a) We used our array CGH data to construct confidence intervals for both the 5′ and 3′ breakpoints of 350 CNVs with published breakpoint sequences. m2 confidence intervals (shown here as 700 horizontal gray lines) are drawn in base pairs 5′ or 3′ (<0 or >0, respectively) from the GADA-estimated breakpoint location. The true location for each sequenced breakpoint is represented as a red dot. There appears to be a strong positive correlation between confidence interval size and the accuracy of the GADA breakpoint estimates, indicating the CGH data contains useful information on the uncertainty in breakpoint location. (b) We confirmed this by modeling the relationship between confidence interval size and the accuracy of our breakpoint estimates. The best-fit line from least-squares regression is shown in red (test of slope = 0, P < 10⁻¹⁵). (c) A permutation test of the hypothesis that our confidence intervals cover more breakpoint locations than expected by chance. As our test statistic, we used the number of true breakpoints covered by a set of confidence intervals. A null distribution for this statistic was generated using 1,000 permutations of m1 confidence intervals across CNVs (shown here as a black curve). The number of true breakpoints covered with the correctly assigned confidence intervals (indicated by a vertical red line) was 13 s.d. greater than the mean from the randomly assigned permutations. (d) The relationship between CNV log₂ ratio between test and reference in the discovery CGH experiment and the breakpoint estimation error indicate that GADA breakpoint estimation accuracy decreases as the CNV signal is closer to the background.