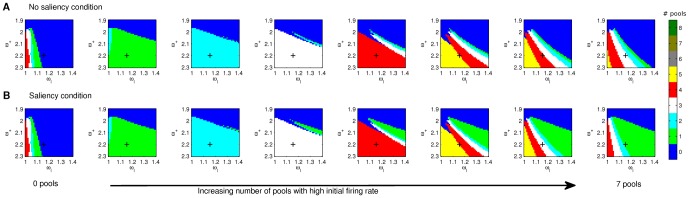
Figure 2. Mean field analysis of the model.
Mean field analysis of the model assessing the dependence of the network behaviour on the potentiated synaptic strength (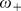 ) and the inhibitory synaptic strength (
) and the inhibitory synaptic strength (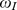 ), for different initial conditions. A The initial firing rate conditions for pools showing high firing rates are derived from a Gaussian distribution with mean
), for different initial conditions. A The initial firing rate conditions for pools showing high firing rates are derived from a Gaussian distribution with mean 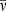 = 40 Hz and standard deviation
= 40 Hz and standard deviation  = 0.01 Hz. The firing rates determining the initial conditions of pools in spontaneous states are obtained from randomly sampling a Gaussian distribution with mean
= 0.01 Hz. The firing rates determining the initial conditions of pools in spontaneous states are obtained from randomly sampling a Gaussian distribution with mean 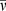 = 3 Hz and standard deviation
= 3 Hz and standard deviation  = 0.01 Hz. The colour code indicates the number of pools which settle on stable states showing persistently high firing rates (
= 0.01 Hz. The colour code indicates the number of pools which settle on stable states showing persistently high firing rates (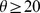 Hz) during the delay period when no further stimulation is provided. B Identical initial conditions as in A but one of the pools showing an initially high firing rate of 65 Hz. From left to right an increasing number of pools had high initial firing rates. Note that as a consequence of considering a hard boundary (i.e.
Hz) during the delay period when no further stimulation is provided. B Identical initial conditions as in A but one of the pools showing an initially high firing rate of 65 Hz. From left to right an increasing number of pools had high initial firing rates. Note that as a consequence of considering a hard boundary (i.e. 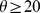 Hz, used in subsequent studies) for values
Hz, used in subsequent studies) for values 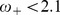 some apparent discontinuities may appear for increasing
some apparent discontinuities may appear for increasing 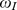 values, which in fact correspond to stable states with persistent firing rates just below the threshold. However, this does not occur in the region where our working point is located (
values, which in fact correspond to stable states with persistent firing rates just below the threshold. However, this does not occur in the region where our working point is located (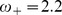 ,
, 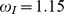 ).
).