Coupling carbon nanotube mechanics to a superconducting circuit

Abstract

The quantum behaviour of mechanical resonators is a new and emerging field driven by recent experiments reaching the quantum ground state. The high frequency, small mass, and large quality-factor of carbon nanotube resonators make them attractive for quantum nanomechanical applications. A common element in experiments achieving the resonator ground state is a second quantum system, such as coherent photons or a superconducting device, coupled to the resonators motion. For nanotubes, however, this is a challenge due to their small size. Here, we couple a carbon nanoelectromechanical (NEMS) device to a superconducting circuit. Suspended carbon nanotubes act as both superconducting junctions and moving elements in a Superconducting Quantum Interference Device (SQUID). We observe a strong modulation of the flux through the SQUID from displacements of the nanotube. Incorporating this SQUID into superconducting resonators and qubits should enable the detection and manipulation of nanotube mechanical quantum states at the single-phonon level.

The remarkable properties of nanoelectromechanical systems (NEMS) are useful for a wide variety of applications, such as ultra-sensitive force detection¹,²,³, mass detection at the single atom level⁴,⁵, and exploring the quantum limit of mechanical motion⁶,⁷,⁸,⁹,¹⁰. For all of these applications, sensitive detection of the resonator motion is crucial. The ultimate limit of the detection of the motion of a mechanical resonator is given by its quantum zero point fluctuations, which result in an uncertainty in the resonators position determined by the standard quantum limit¹¹.

An effective way of detecting the quantum motion of mechanical devices is to couple their displacement to another “probe” quantum system which can be read out and controlled, such as coherent quantum states of a superconducting qubit⁸, coherent photons in a cold microwave resonator circuit⁹, or the coherent fields of a laser¹⁰. In the last decade, superconducting circuits have emerged as an established platform for engineering and controlling quantum behaviour¹². This has formed the motivation for many works coupling MEMS and NEMS devices to superconducting circuits⁸,⁹,¹¹,¹³,¹⁴,¹⁵. By coupling microelectromechanical (MEMS) devices to quantum superconducting circuits, researchers have recently demonstrated mechanical resonators in their quantum ground state⁸,⁹ and achieved single-phonon control over their motion⁸. An outstanding challenge in these experiments is simultaneously achieving both a strong coupling at the single-phonon level, together with a high frequency and large quality factor for the mechanical resonator.

Carbon nanotube mechanical resonators¹⁶,¹⁷,¹⁸ posses a unique combination of large quality factor, small mass, and high frequency. Because of their small size, however, it is not easy to couple to their quantum motion. Techniques based on a capacitive interaction with superconducting qubits or microwave photon cavities, as was done in recent experiments with MEMS devices reaching the mechanical quantum ground state⁸,⁹, do not provide sufficient coupling strength. An alternative is to incorporate the mechanical element into a SQUID, as was demonstrated recently using micromechnical beams¹⁹. If a carbon nanotube NEMS element could be included in a SQUID, the SQUID could then be used as a transducer to couple the mechanical motion to a superconducting cavity²⁰, or as the basis for a superconducting qubit, coupling the motion directly to the qubit quantum states.

Results

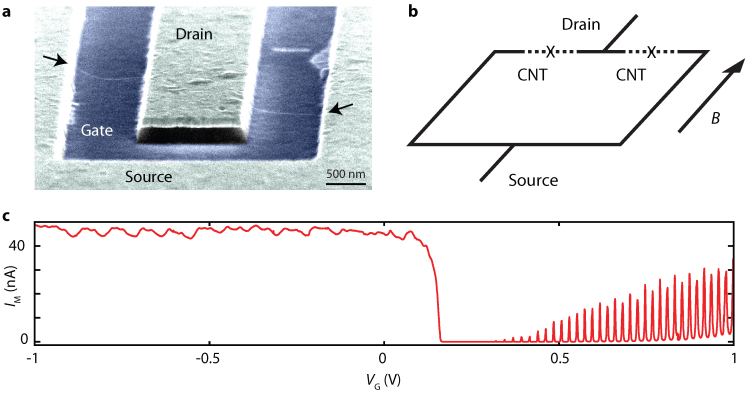
Here, we demonstrate the coupling of a carbon nanotube NEMS device to a superconducting circuit, based on a suspended carbon nanotube SQUID. The device consists of a SQUID in which the two Superconductor-Normal metal-Superconductor (SNS) weak links are made from carbon nanotube junctions²¹,²²,²³. In contrast to earlier works, the carbon nanotubes are freely suspended, and thus also act as NEMS elements embedded in the SQUID. To make the suspended nanotube SQUID, a clean carbon nanotube is grown in the last step of fabrication²⁴ over a trench patterned between metal source and drain contacts made from a MoRe superconducting alloy (see Methods). A Scanning Electron Microscope (SEM) image of a typical device is shown in Fig. 1a. The doped substrate below the trench is used as a global backgate. The device is mounted in a superconducting magnet coil with the magnetic field aligned in the plane of the sample, parallel to the trenches, as indicated in Fig. 1b. The magnetic field orientation is chosen to maximize the coupling of vertical displacements on the nanotube to flux in the SQUID loop¹⁹. A small misalignment of the sample also induces a magnetic field perpendicular to the sample surface which is used to tune the flux operating point of the SQUID.

Figure 1. Design and characterization of the device.

(a) Colorised scanning electron microscope (SEM) image of a typical device showing a single carbon nanotube (CNT) crossing two trenches. The device is made by etching two 800 nm wide trenches in a MoRe layer and underlying SiO₂, and subsequently growing CNTs over the prefabricated structure. We apply a voltage V_G to the doped substrate underneath the SiO₂, which acts as a gate. (b) Schematic drawing of the SQUID. The two suspended segments of the CNT form two SNS-type Josephson junctions, indicated by the crosses. An external magnetic field B can be applied in-plane along the trench. (c) I_M as a function of V_G measured with an applied source-drain bias voltage V_B = 2 mV. For V_G > 0.3 V, the suspended segments form a p-n-p quantum dots exhibiting Coulomb blockade. For V_G < 0.2 V, the CNT is doped with holes, showing Fabry-Perot oscillations with high conductance.

Figure 1c shows the current through the device (I_M) as a function of the applied gate voltage (V_G). From the gate voltage thresholds for electron and hole conduction, we estimate that the carbon nanotube has a small bandgap of 40 meV (see Supplementary Information). Due to a work function difference present between the nanotube and the metal contacts, the nanotube is doped with holes near the edge of the trench. At positive gate voltages, electrons induced by the gate are confined by p-n junction tunnel barriers²⁴ in a Coulomb-blockaded quantum dot. For negative gate voltages, holes are induced in the suspended segment with no tunnel barriers. Here, instead of Coulomb blockade, conductance oscillations arising from Fabry-Perot electronic interference²⁵ are observed with conductances of up to 4.7 e²/h (see Fig. 2a). Note that this value exceeds the maximum conductance expected for a single carbon nanotube (G_max = 4 e²/h), consistent with a SQUID geometry (Fig. 1b) where there are two carbon nanotube junctions in parallel (Fig. 1a).

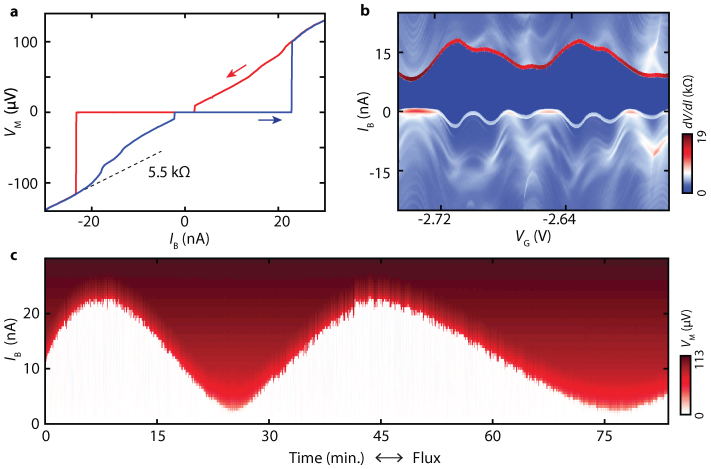
Figure 2. A suspended carbon nanotube SQUID.

(a) Four-terminal current-voltage trace at V_G = –1.1 V. The onset of the resistive branch occurs at 24 nA, corresponding to a critical current of 12 nA per nanotube junction. The dashed line indicates the normal-state resistance of 5.5 kOhm (G = 4.7 e²/h). The device is hysteretic, as can be seen from the forward (blue) and reverse (red) sweep directions²⁶. (b) Differential resistance dV_M/dI_B (color map) as a function of I_B and V_G (forward sweep direction). The critical current (red stripe at positive I_B) oscillates with V_G, following the modulation of the normal state conductance. (c) SQUID voltage V_M as a function of applied current I_B and time, taken at B = 0 and V_G = –1.1 V. Flux creep in the superconducting magnet coil is used to apply a small time varying magnetic field. The critical current oscillates from 2 nA up to 24 nA as a function of the flux through the SQUID. The near complete suppression of I_C at the minima indicates that the SQUID has highly symmetric junctions.

In Fig. 2, we use the gate to dope the nanotube with holes such that the device is tuned into the high-conductance Fabry-Perot regime, and measure the voltage across the SQUID as a function of an applied bias current (Fig. 2a). At low currents, the voltage across the device is zero, a clear indication of a proximity effect induced supercurrent. At a critical current of 24 nA, there is a switch to a finite voltage state. We attribute the large critical current in our junctions (12 nA per nanotube) to the high critical temperature of the superconducting metal leads (T_C = 5.5 K), the low contact resistance between the superconducting metal and the nanotube, and the clean electronic characteristics of the carbon nanotube. As shown in Fig. 2b, the critical current is strongly modulated by the gate through to gate dependence of the normal-state conductance²¹. Due to the high transparency of the superconductor-nanotube interface, the supercurrent in our device also remains finite in the valleys between the peaks in conductance.

To demonstrate that the device acts as a SQUID, we measure the critical current as a function of the flux through the loop. In practice, we do this by sweeping a large in-plane magnetic field to zero and then subsequently measure the critical current as a function of time. Due to creep in the superconducting magnet coil and the slight misalignment of the field to the sample plane, there is a small magnetic field component perpendicular to the surface that continues to change slowly after the sweep is completed. In such a measurement, shown in Fig. 2c, the observed critical current oscillates between a value of 24 nA and 2 nA. These oscillations result from quantum interference of the superconducting wavefunction traversing the two junctions of the SQUID²⁶. The large sensitivity of the critical current to the flux from the small magnetic field creep, together with the single periodicity, is consistent with a single large SQUID loop formed by one nanotube SNS junction across each trench, as shown in the SEM image of a typical device in Fig. 1a.

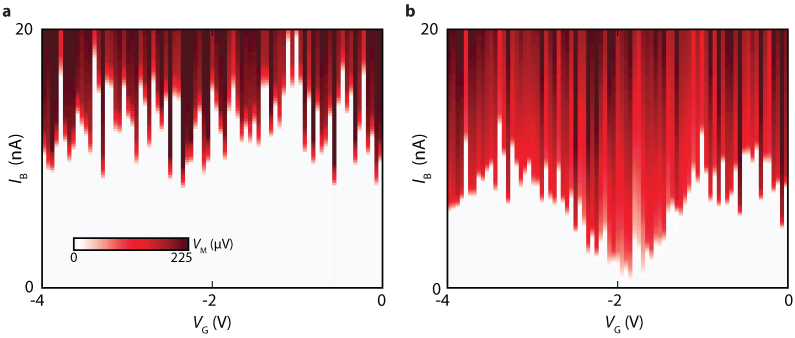
We now turn our attention to the behaviour of the device in the presence of a static in-plane magnetic field applied parallel to the trench. Figures 3a and 3b show the gate voltage dependence of the critical current with and without an external magnetic field. The measurements are taken intentionally with a coarse gate voltage resolution such that the measurement time is short compared to the timescale of the flux creep (see Supplementary Information for further details). The steps in gate voltage are much larger than the periodicity of the Fabry-Perot conductance oscillations (Fig. 2a); consequently, these appear in Fig. 3a as (reproducible) single-pixel fluctuations. Figure 3b shows the same measurement taken at an external magnetic field of 250 mT. Here, an additional nearly sinusoidal modulation of the critical current can be seen as a function of gate voltage with a periodicity much longer than that of the Fabry-Perot conductance oscillations.

Figure 3. A gate-voltage induced magnetic flux.

(a) Colormap of V_M as a function of I_B and V_G, taken at B = 0 T. The critical current I_C is defined by the onset of a finite voltage state, indicated by the red regions. The Fabry-Perot modulation of the critical current (Fig. 2b) is visible as rapid fluctuations in I_C due to the large steps in V_G. The measurement is performed fast enough such that the magnetic field creep (Fig. 2c) can be neglected. (b) Same measurement taken at B = 250 mT. An additional approximately sinusoidal modulation of the critical current is seen with a gate periodicity of ΔV_G = 2.5 V.

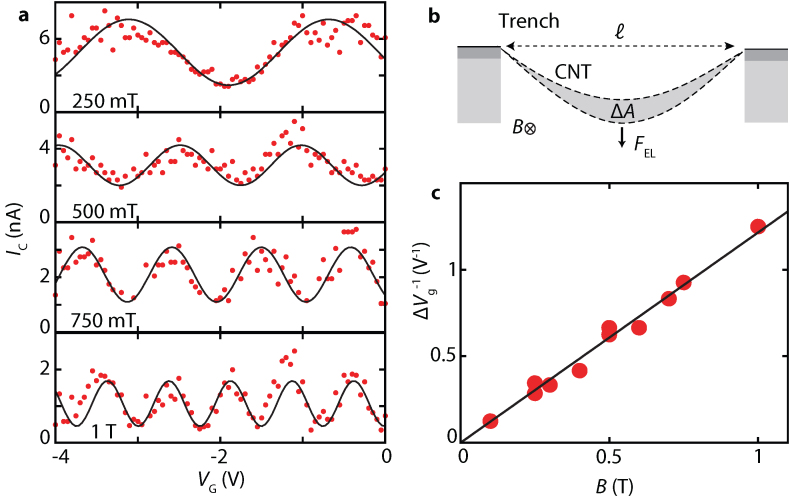
In the following, we show how this additional gate modulation of the critical current arises from a change in magnetic flux induced by the d.c. gate voltage. The mechanism for such a gate induced flux is illustrated in Fig. 4b. Increasing the gate voltage, the nanotube is pulled towards the gate by the attractive electrostatic force between them. The nanotube displacement introduces an extra area ΔA of the SQUID loop perpendicular to the magnetic field aligned along the trench. This area change results in a flux change linearly proportional to the displacement, 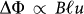, where B is the in-plane magnetic field, 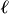is the nanotube length, and u is the vertical displacement of the nanotube. If the displacement u is linear in the gate voltage (as expected for certain gate voltage ranges, see Supplementary Information for further discussion), the critical current of the SQUID will then oscillate as a function of gate voltage with constant periodicity, as observed in Fig. 3b.

Figure 4. Mechanical flux coupling.

(a) Extracted I_C (dots) as a function of V_G at four different magnetic fields. Lines show a sinusoidal fit to the data (red points) from which the periodicity 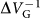is extracted. At B = 1 T, five oscillations are visible corresponding to a flux change of 5 Φ₀. (b) Vertical displacement of the nanotube due to the electrostatic force from the gate changes the area of the SQUID loop perpendicular to the in-plane magnetic field. This produces a gate-induced flux change proportional to the nanotube displacement, resulting in an I_C that oscillates with V_G. We estimate that the nanotube displaces by 7.4 nm as V_G is swept from 0 to −4 V (ΔA ~ 5.5 × 10^–3 µm² per nanotube). (c) 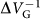(dots) as a function of magnetic field with a linear fit (black line). At B = 1 T, the flux couples to the vertical displacement of the nanotube with a flux coupling of 0.36 mΦ₀/pm.

If this gate-voltage induced flux indeed arises from a mechanical displacement of the nanotube, the flux coupling should scale linearly with the external magnetic field. Figure 4a shows the extracted I_C versus V_G for fields up to 1 T. To extract the gate periodicity of the flux oscillation, the critical current as a function of gate voltage is fit to a sinusoidal function in order to approximate the expected oscillatory SQUID response²⁶. The resulting gate frequency 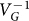is plotted as a function of magnetic field in Fig. 4c. The linear scaling of the periodicity with magnetic field demonstrates that the modulation is due to a flux originating from the mechanical displacement of the nanotube. At magnetic fields of 1 T, we couple the motion of the nanotube to the flux in the SQUID with a coupling strength of 0.36 mΦ₀/pm (see Supplementary Information).

Discussion

In the previous section, we demonstrate a strong coupling of the flux in a SQUID to the displacement of the carbon nanotube NEMS device. The strong flux coupling is, on its own, not unique to our device: for example, a larger mechanical flux responsivity was observed in a top-down fabricated SQUID¹⁹. What is unique to our device is the combination of such a flux coupling with a mechanical resonator with small mass (attogram) and large zero point fluctuations. This can be quantified in terms of the amount of flux noise the mechanical zero-point fluctuations would induce in the SQUID. The expected zero point motion of the nanotube is on the order of 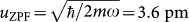. Together with a quality factor of 3 × 10⁴ and a mechanical resonance frequency of 125 MHz observed in this device (see Supplementary Information), this results in a peak in the flux noise spectrum of the SQUID at the mechanical resonance frequency with an amplitude of 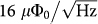. This noise level, corresponding to the imprecision noise from the standard quantum limit for our device, is nearly two orders of magnitude larger than the 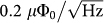sensitivity that has been demonstrated coupling a SQUID to a superconducting resonator²⁷. Doing so, we expect that such a high frequency suspended carbon nanotube SQUID can be used as a linear position detector with an imprecision noise below the standard quantum limit, enabling the detection of the quantum motion of a carbon nanotube.

Finally, the strong coupling between flux and nanotube displacement could also be used to implement a nanomechanical resonator coupled to a superconducting qubit. The important characterization of the coupling between the two quantum systems is the zero-phonon coupling rate g, given by the energy shift of the probe quantum system in response to the zero-point fluctuations of the mechanical device¹⁰. In order to have a coherent interaction between the probe and the mechanical system at the single-phonon level, the coupling rate g must be larger than the decoherence rates of quantum states of the mechanical system and probe system. Incorporating a nanotube SQUID into a transmon-qubit design would achieve a single-phonon coupling rate of g = 7 MHz (see Supplementary Information). Such a coupling strength would be within the single-phonon strong-coupling limit, providing a means for the readout and control of mechanical quantum states of a carbon nanotube.

Methods

Fabrication begins with an oxidized p++ Si wafer (285 nm oxide), in which the doped substrate is used as a global backgate. A 40/40 nm Mo/Re bilayer is deposited by magnetron sputtering, and electrodes are subsequently defined by reactive ion etching with an SF₆ plasma. Reactive ion etching is continued into the substrate, also defining self-aligned trenches in the SiO₂. The Mo and Re in the two separate layers subsequently alloy together during the nanotube growth step. The resulting film is a superconductor with a T_C of 5.5 K. Nanotubes are grown over the structure in the last step using a methane CVD growth²⁴, and promising devices are selected from room-temperature electrical characterization. Measurements are performed in a dilution refrigerator at a base temperature of 25 mK. The device is connected via copper powder filters and low pass filters at base temperature to the measurement equipment at room temperature. Measurements are performed in either a 4-terminal current bias or a 2-terminal voltage bias configuration.

Author Contributions

B.H.S. fabricated the sample. B.H.S. and S.E. conducted the experiments. B.H.S. and G.A.S. wrote the manuscript. G.A.S. and H.S.J.v.d.Z. supervised the project. All authors discussed the results, analyzed the data, and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information