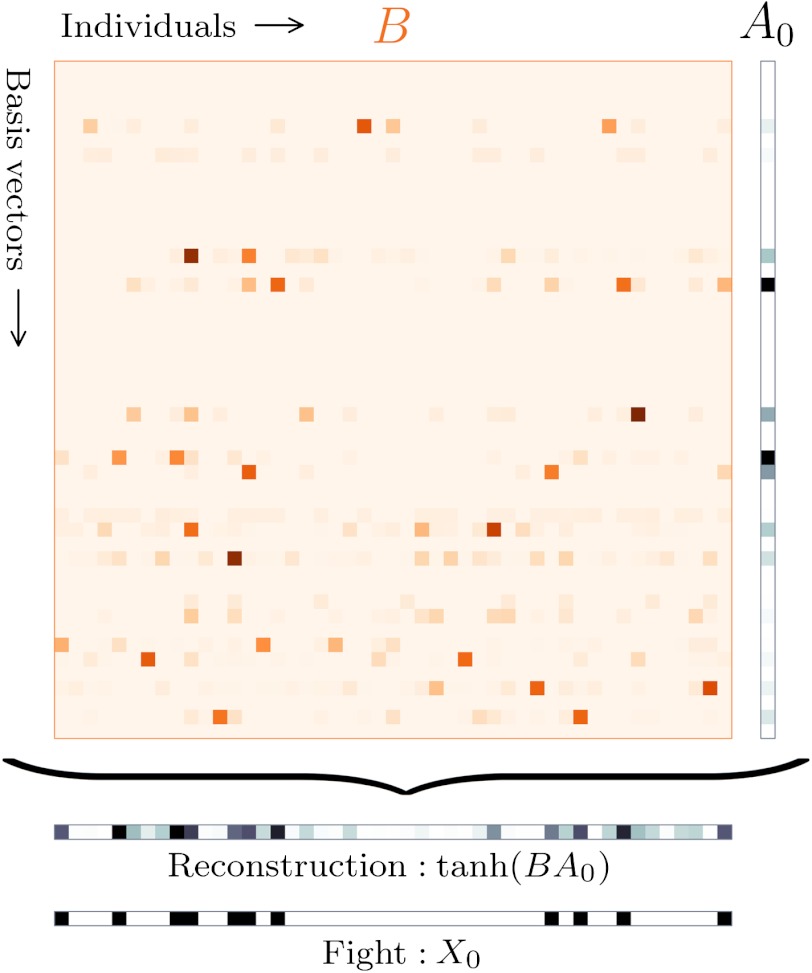
Fig. 1.

Representing a fight using a sparse basis. To represent a fight X₀, coefficients A₀ define a sparse linear combination of basis vectors BA₀ that is passed through the nonlinear activation function tanh. Here λ has been tuned to produce optimal out-of-sample predictions; note that this produces sparse basis vectors that consist of small sets of individuals. Sparsity of the data implies that if one knows B and only the few active elements of A₀, one can come close to reconstructing the entire fight. Furthermore, by remembering B, the likelihood of future fights can be estimated by determining the necessary magnitudes of coefficients A₀: fights that can be represented using fewer large coefficients are more likely. In this figure and in Fig. 5, darker colors represent elements with larger magnitude (see Materials and Methods).