Abstract
Solvation analysis is one of the most important tasks in chemical and biological modeling. Implicit solvent models are some of the most popular approaches. However, commonly used implicit solvent models rely on unphysical definitions of solvent-solute boundaries. Based on differential geometry, the present work defines the solvent-solute boundary via the variation of the nonpolar solvation free energy. The solvation free energy functional of the system is constructed based on a continuum description of the solvent and the discrete description of the solute, which are dynamically coupled by the solvent-solute boundaries via van der Waals interactions. The first variation of the energy functional gives rise to the governing Laplace-Beltrami equation. The present model predictions of the nonpolar solvation energies are in an excellent agreement with experimental data, which supports the validity of the proposed nonpolar solvation model.
INTRODUCTION
Under physiological conditions, water constitutes 65%–90% of cellular mass. As such, essentially all important biological processes, including signal transduction, transcription, and translation, occur in an aqueous environment. Therefore, an elementary requirement for quantitative modeling and analysis of biological processes is a detailed understanding of the solvation process, in which solute molecules are transferred from their lowest energy state in vacuum to an equilibrium state in a solvent environment.1, 2, 3, 4 The solvation process involves the work of inserting a molecule into the solvent and a range of possible solvent-solute interactions at the interface, including hydrogen bonding, ion-ion, ion-dipole, dipole-dipole and multipole attractions, Debye attractions, and London dispersion attractions. These interactions induce structural reorganization of the solvent near the interface as well as possible solute configurational changes.
Experimental techniques, such as neutron diffraction with isotopic substitution and anomalous x-ray diffraction, have been applied to determine the solvent atomic distribution in the vicinity of the interface. A vast range of computational approaches has also been developed to predict the solvent microstructures. In molecular mechanics, the solvent can be described with a variety of sites, different levels of bond flexibilities, different orders of multipole expansions, and many quantum mechanical treatments.5, 6, 7, 8, 9 For example, solvent microstructure can be extracted from molecular dynamics simulations and described by density distribution and correlation functions.10, 11, 12 These functions can also be described by the density functional theory13 and/or integral equations.14, 15 In general, both molecular mechanical and statistical mechanical based microstructural theories are capable of predicting solvent radial distribution functions, surface tension, temperature, and pressure.16, 17, 18, 19
The calculation of solvation free energy has captured a great deal of interest with research developing solvation models ranging from simple phenomenological modifications of Coulomb's law, implicit solvent models that describe the solvent by mean-field approximations,20, 21, 22, 23, 24 explicit solvent models that treat the solvent in molecular or atomic detail,1 to complex quantum mechanical methods.2, 25, 26, 27 Each of these models has its own domain of applicability, merits, and limitations. Explicit and quantum methods are ideal for studying the solvation of relatively small molecules, but involve an excessively large number of degrees of freedom for large molecules, which can become prohibitively expensive. Implicit solvent methods and, especially multiscale methods which are able to reduce the number of degrees of freedom, are indispensable in solvation analysis and the quantitative description of other biological processes in general.
An essential element in all implicit solvent models is the description of the interface that separates the solute from the solvent.28 Many solvation quantities of physical interest, including electrostatic free energies, surface areas, cavitation volumes, solvation free energies, and pKa values, are very sensitive to the interface definition. Currently, a number of different surface definitions, including the van der Waals (vdW) surface, the solvent accessible surface,29 the solvent excluded surface,30 and electron density isosurface are used in implicit solvent analysis, and have had much success in biomolecular modeling,31, 32, 33, 34, 35, 36, 37, 38 including protein folding,31, 32 protein-protein interfaces,33 protein surface topography,34 oral drug classification,35 DNA binding and bending,36 macromolecular docking,37 and enzyme catalysis.38 However, these surface definitions are ad hoc partitions to separate solute atoms from the surrounding solvent, and often create geometric singularities.39 Currently, there is no consensus about which surface should be used to describe the solvent-solute boundary in implicit solvent models.
In the past few years, a series of efforts has been taken to improve the surface description of implicit solvent models. The first effort was the introduction of curvature driven partial differential equations (PDEs), i.e., geometric flows, to construct singularity free protein molecular surfaces in 2005.40 This has led to the recent surge in PDE based approaches for molecular surface analysis. The next step was the introduction of the minimal molecular surface (MMS), obtained by using variational principles and the mathematical theory of geometric flows, namely, the mean curvature flow.41, 42 The MMSs are able to minimize the surface free energy of a macromolecule in solution. A natural step to improve the minimal molecular surface model was to consider more solvent-solute interactions in the surface construction by using potential-driven geometric flows.43 Recently, differential geometry based multiscale models have been introduced for the analysis of structure, dynamics, and transport of complex chemical and biological systems.44 An essential ingredient of such models is the use of the differential geometry of surfaces as a natural means to separate the continuum solvent domain from the atomistic solute domain, while dynamically coupling discrete descriptions and continuum descriptions. The main strategy is to construct a total energy functional of the system to encompass the polar and nonpolar free energies of solvation, and other energies of interest. Intensive investigation has been carried out to practically implement differential geometry based solvation models in the Eulerian representation,45 Lagrangian representation,46 and quantum formulation.47 These models incorporate solvent-solute van der Waals interactions and thus, partially take care of solvent size effects near the interface. They have been extensively validated with experimental data of solvation free energies.45, 46, 47 While these solvation models are similar to those of Dzubiella et al. in spirit,48, 49 the treatment of surface tension is different in the two approaches. Most recently, generalized correlations have been considered in differential geometry based multiscale models to account for not only solvent-solute interactions, but also ion-ion and ion-solute interactions.50 These multiscale models, in principle, should be able to capture the solvent microstructure. However, these differential geometry based multiscale models involve polar and nonpolar solvation components, and chemical potential type of energies, which can contribute to uncertainty in the model validation and quantification.
The objective of the present work is to minimize modeling uncertainty in the differential geometry based multiscale models by considering a relatively isolated situation where electrostatic interactions do not play an important role. A specific physical process is the solvation of nonpolar molecules, in which the electrostatic interactions between solvent and solute are negligible. This simplified situation constitutes a test of whether the differential geometry based framework provides a viable description of solvation free energies. Note that in the present approach, while an atomistic description is utilized for the solute, the solvent domain is treated as a continuum.
The rest of this paper is organized as follows. Section 2 is devoted to the formulation of the present differential geometry based nonpolar solvation model. We present a variational framework for the solvation free energy contributions. The governing equation is derived by the Euler-Lagrange variation. The solution of the governing equation gives rise to the solvent-solute boundary, which facilitates solvation free energy calculation. We design schemes of second-order numerical accuracy for the construction and evolution of solute characteristic function. Appropriate iterative procedures are provided to ensure convergence of the solution. Section 3 presents validation and analysis of the proposed new solvation model. The applications of the proposed theories, methods and algorithms are considered to two sets of compounds: alkanes and alkenes. Comparison is given to experimental measurements and results in the literature. Finally, this paper ends with a conclusion.
THEORY AND ALGORITHM
Theoretical model
In this work, we investigate the physical boundary between solvent and solute by considering a realistic problem with less uncertainty. Specifically, we apply our variational approach to apolar molecules that admit negligible polar solvation effects. Nonpolar solvation processes are generally associated with the insertion of an uncharged solute into solvent. There are many nonpolar solvation models available. The most commonly used model is the scaled particle theory (SPT) (Ref. 22) which includes the energy of the surface tension effect and the mechanical work of immersing a particle into the solvent. Recent work by Levy, Gallicchio, and others3, 4, 51 has demonstrated the importance of attractive solute-solvent terms as well as models of solvent-solvent repulsive interactions, in addition to both area and volume contributions.51 In the present work, we employ the following model for nonpolar solvation free energies:51
| (1) |
where γ is the surface tension, Area is the solvent-excluded surface area of the solute, p is the hydrodynamic pressure, Vol is the solvent-excluded volume of the solute, ρs is the solvent density, Ωs denotes the solvent accessible region, and UvdW(r) is the solvent-solute vdW interaction potential. The first two terms in Eq. 1 are those from the SPT.22 Since the division of polar and nonpolar solvation energies is somewhat arbitrary, the polar contribution might not be completely excluded in real situations. Nevertheless, the attractive van der Waals interactions can offset possible small polar contributions. This nonpolar solvation model has been shown to provide a good agreement for the solvation forces of proteins51 and RNA hairpins23 with explicit solvent models. Levy and co-workers have demonstrated good performance of a similar nonpolar model.3, 4, 52, 53
The free energy functional 1 provides a method for practical nonpolar solvation analysis. Moreover, a variational principle based on 1 leads to a potential-driven geometric flow equation for the surface evolution46
| (2) |
where is a position vector on the evolving manifold Γ, N is the outward unit normal direction at X, and the potential Wn ≡ −2γH + p − ρsUvdW vanishes upon optimization of the free energy functional 1 with respect to the solvent-solute interface Γ. Here, H is the mean curvature of Γ. The generalized geometric flow equation 2 is in the Lagrangian formulation. The numerical solution of 2 involves the evolution of a triangularization mesh representing the solvent-solute interface. The advantage of such a Lagrangian approach is that it evolves only a two-dimensional surface. The Lagrangian approach encounters difficulties in handling topological changes, such as surface breaking or merging, which commonly occur in biomolecular surface constructions and molecular dynamics applications. However, one can overcome these obstacles by using the Eulerian formulation,40, 41, 42, 43 in which the surface is embedded into a higher dimensional space as a level set of higher dimensional surface. Then the topological changes can be easily handled.
Governing equations in Lagrangian and Euler formulations
In the Lagrangian formulation, the potential driven geometric flow equation of the solvent-solute interface is given by Eq. 2. The total free energy is known to be decreasing when the surface is evolved by 2 (Ref. 46) and the steady state solution of Eq. 2 yields a solvent-solute interface with Wn = 0.
In the Eulerian formulation, the interfacial surface is embedded in a hypersurface and the latter is evolved under prescribed driving forces. Consider a hypersurface function S(r) with . Then the desired surface can be represented as a set of points with a constant value of function S,
| (3) |
where L is an isosurface value. On an isosurface, ∇S vanishes along two tangential directions. Thus, the normal direction at r is given as
| (4) |
Moreover, the explicit form of mean curvature can be obtained according to the equality 2H = ∇ · N,
| (5) |
By the Chain Rule
| (6) |
Substituting from 4, one has
| (7) |
Finally, by using 5, we arrive at the Eulerian form of the proposed potential driven geometric flow equation for the solute-solvent interface
| (8) |
The vdW potential UvdW is computed pairwise for each atom , where is the standard 12-6 Lennard-Jones potential for the ith particle of the solute at ri and the solvent at position r. Here, σs represents the solvent radius, σi is the radius of the ith particle of the solute, and εi the well-depth. In this work, is taken as the attractive part of the Lennard-Jones potential according to the Weeks-Chandler-Anderson (WCA) theory.45, 46, 54 σi is taken as the solute atomic radius and σs is fixed to be 0.65 Å as a calibrated solvent radius.51 To determine all the well-depth parameters in UvdW, we assume that the Lennard-Jones potential is a constant when sampling on the vdW surface of the ith atom.45, 46 Therefore, we set . The atom-dependent well depth parameters εi are determined if , which is used as a fitting parameter, is known. In general, each should admit a different value for each type of atom, however, we feel that the loss of generality in taking them equal is small while computational savings are great.
The computation of the proposed nonpolar solvation model is carried out in two steps. At the first step, the potential driven geometric flow equation 7 is numerically solved by using the finite difference method. A brief description of this solution procedure is given here, and we refer to our earlier works42, 45 for more details. We first rewrite equation 8 as
| (9) |
where t′ = tγ. Two modifications have been conducted. First, to avoid a vanishing value in the denominator, ‖∇S‖ is replaced by . Such a replacement will not affect the optimized solvent-solute interface, because ‖∇S‖2 is much larger than one near the interface. Second, the temporal variable is scaled by γ. We note that the free parameters of this equation are essentially the surface tension γ, hydrodynamic pressure constant p, and solvent density ρs.
Consider a macromolecule with total Na number of atoms. All geometric structures of compounds considered in this work are taken from the pubchem web (http://pubchem.ncbi.nlm.nih.gov). vdW radii are set as 1.87 Å, which is ZAP-9 radius,55 for the carbon atom and 1.10 Å for the hydrogen atom. We denote the center and radius of the ith atom to be ri = (xi, yi, zi) and ri, respectively, for i = 1, 2, …, Na. We then define the domain enclosed by the solvent accessible surface to be , where rp is the probe radius. For the initial value of S, we consider an indicator function
| (10) |
where S0 = 1000. The explicit Euler method and the second-order central difference scheme are used for temporal and spatial discretization, respectively. We only numerically update the values of S(x, y, z, t) at the points in between the vdW surface and solvent accessible surface, i.e., . This is for the purpose of protecting the van der Waals surface and making the computation more efficient. After the steady state solution is numerically reached, the solvent-solute interface Γ can be represented as a set of points with a constant value of function S, Γ = {r|S(r) = L}. Here, the isosurface value is chosen to be .
In the second step, we calculate the nonpolar solvation free energy based on the solvent-solute interface Γ. For this purpose, we need to compute surface integrals and volume integrals over the solute domain Ωm, which are defined originally in the Lagrangian formulation. However, the hypersurface function S is defined on a three-dimensional (3D) Cartesian grid in the Eulerian formulation. Consequently, the isosurface Γ is also represented based on the 3D Cartesian grid. Therefore, great care has to be exercised when calculating these integrals.
Surface extraction
A stand-alone algorithm based on the marching cubes method56 is constructed. Consider a grid point (xi, yj, zk) on the 3D Cartesian grid and denote Si, j, k = S(xi, yj, zk). We first compute a normal vector n = (nx, ny, nz), according to S values nearby,
| (11) |
The surface integral of a density function f can be approximated by57
| (12) |
where δ(d) is a delta function and d is distance of a point (x, y, z) defined in Ω from the interface Γ. By means of the delta function, the surface integral becomes a volume integral in the entire domain, and the latter is numerically approximated based on discrete function values f(xi, yj, zk) and a 3D discrete delta function . Here, for simplicity, we assume a uniform mesh size h along x, y and z directions. Generalization to a nonuniform mesh is possible. Following Smereka, the 3D discrete delta function is taken to be
| (13) |
where are 1D discrete delta functions.57 For a node (xi, yj, zk), these six 1D delta functions are never present simultaneously. For a reasonable mesh resolution, at most three of them could be seen.
We restrict our following discussions from one side of interface, say inside the interface. Consider all grid points which are either on the interface, or are inside the interface but whose distance away from the interface is less than h. Denote the set of such grid points to be I. To carry out integration exactly on the interface, we use the following discrete surface integration formula:57
| (14) |
where (xo, yj, zk) is the intersecting point of the interface and the x meshline that passes through (i, j, k), and nx is the x component of the unit normal vector at (xo, yj, zk). Similar relations exist between (xi, yo, zk) and ny, and (xi, yj, zo) and nz. The interface locations and normal directions are calculated by linear interpolation. For instant, if (xi, yj, zk) ∈ I and (xi+1, yj, zk) is outside the interface, we calculate a scaled distance from the interface to be
| (15) |
Then the function value and the normal direction can be computed as
| (16) |
The unit normal No at the intersecting point can be easily computed as , whose x component is nx in 14. Other terms in 14 can be similarly approximated.
The surface area can be calculated by setting f = 1 in Eq. 14. The error of the surface integration depends on the grid resolution and was observed to be approximately second-order in h.57 The volume integral of the density function f can be simply approximated by57
| (17) |
where J1 is the set of grid points inside/on the surface, and J2 contains the points outside the surface while adjacent to at least one point belonging to J1.
Iteration procedure
Essentially, the model involves three optimization parameters: the surface tension γ, hydrodynamic pressure p and the Lennard-Jones potential parameter . An iterative procedure is used to optimize three model parameters γ, p, and :
Choose a trial set of molecules with given atomic coordinates, radii, and experimental data of solvation free energies. For each molecule, take an initial set of parameters γ, p, and .
For jth molecule, solve Eq. 2 to a steady state to compute surface area, molecular volume, and solvation free energy .
- Set up a target function
where are experimental data of solvation free energies. Parameters p, γ, and are updated by resolving a least-squares problem to determine non-negative parameters. The iterative procedure continues until the target function T reaches within a pre-set tolerance for the above three parameters.
Numerically, we have found that the above iterative procedure is not sensitive to the initial values of γ, p, and . The same procedure can be applied to allow each to vary independently, which may offer better results. However, it would require a large training set to determine many extra parameters in the nonpolar model.
RESULTS AND DISCUSSIONS
We validate the proposed nonpolar variational approach by conducting both numerical calibration and prediction studies for 11 alkanes, see Table 1. All geometric structures of compounds considered in this work are taken from the pubchem web (http://pubchem.ncbi.nlm.nih.gov). The solvent density is set to ρs = 0.033428 Å−3.51 The potential driven geometric flow equation is numerically solved by using the explicit Euler method for time and the second-order central finite difference scheme for space. In all calculations, we choose a uniform grid spacing h = 0.25 Å in all Cartesian directions and a time stepping τ = h2/4.5. Based on the resulting surface Γ, the solvation free energy Gnp can finally be determined by calculating volume and surface integrals according to 1.
Table 1.
Decomposition analysis for the calibration set of 11 alkanes. Comparisons between our variational approach and the explicit solvent model in Ref. 4 with respect to repulsive and attractive parts and total solvation free energies are conducted. The error in total free energy is calculated according to the experimental data.58
| Rep. part (kcal/mol) |
Att. part (kcal/mol) |
Total (kcal/mol) |
Error (kcal/mol) |
|||||
|---|---|---|---|---|---|---|---|---|
| Compound | Present | Explicit | Present | Explicit | Present | Explicit | Present | Explicit |
| Methane | 4.71 | 5.72 | −2.73 | −3.31 | 1.98 | 2.41 | −0.02 | 0.41 |
| Ethane | 6.65 | 8.07 | −4.75 | −5.44 | 1.90 | 2.63 | 0.07 | 0.80 |
| Butane | 10.30 | 10.10 | −8.18 | −7.21 | 2.12 | 2.89 | 0.04 | 0.81 |
| Propane | 8.50 | 12.19 | −6.45 | −8.98 | 2.04 | 3.21 | 0.08 | 1.25 |
| Pentane | 12.19 | 14.22 | −9.82 | −10.77 | 2.37 | 3.45 | 0.04 | 1.12 |
| Hexane | 14.03 | 16.17 | −11.54 | −12.38 | 2.50 | 3.78 | 0.01 | 1.30 |
| Isobutane | 10.14 | 11.91 | −7.97 | −8.88 | 2.16 | 3.03 | −0.36 | 0.51 |
| 2-methylbutane | 11.73 | 13.64 | −9.35 | −10.13 | 2.38 | 3.51 | 0.00 | 1.13 |
| Neopentane | 11.81 | 13.62 | −9.20 | −10.39 | 2.61 | 3.23 | 0.11 | 0.73 |
| Cyclopentane | 10.60 | 12.79 | −9.43 | −9.99 | 1.17 | 2.80 | −0.03 | 1.60 |
| Cyclohexane | 12.05 | 14.00 | −10.78 | −11.66 | 1.27 | 2.34 | 0.04 | 1.11 |
Based on different initial values, the optimized fitting parameters for alkanes are consistently found to be γ = 0.0806 kcal/(mol Å2), p = 0.0191 kcal/(mol Å3), and kcal/mol. Note that when kcal/mol the depth of potential well εH of hydrogen is 0.046 kcal/mol, which is of the same order of magnitude as that used in the literature.59, 60
In the calculation of alkenes, we take parameters p and values from the alkane calculation by assuming the same solvent behavior. Therefore, only the surface tension γ is regarded as a global fitting parameter here. The parameter optimization based on seven alkene compounds converges to γ = 0.0775 kcal/(mol Å2).
An example plot of the surface evolution for a nonpolar compound is illustrated in Fig. 1. It is seen that the final surface is smooth and free of geometric singularity.
Figure 1.
The schematic plot of the surface evolution of a nonpolar compound (2,2,4-trimethylpentane) with respect to the time.
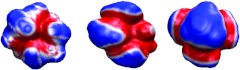
The solvent-solute dispersion term is crucial in the present nonpolar model. The Lennard-Jones potential according to the WCA theory46, 54 is used for the vdW potential. In Fig. 2, vdW potentials UvdW(r) are plotted on the final surfaces for three nonpolar compounds. Clearly, surface vdW potentials differ much from surface electrostatic potentials computed by the Poisson model.
Figure 2.
The final isosurfaces of four nonpolar compounds projected with the corresponding vdW potential. Involved compounds are 1,1-diethoxyethane, bis-2-chloroethyl ether and dimethoxymethane, from left to right.
To benchmark our model, we consider nonpolar molecules which have high quality experimental data of solvation free energies. We first consider a calibration study of alkane compounds. A set of 11 small alkane compounds is chosen which includes linear, branched, and cyclic apolar compounds so that subtle differences are expected in the solvation free energy for the compounds with the same molecular formula. This test set has been frequently used in the literature for the hydrophobic solute test4, 51 because experimental data is available.58 Moreover, the work of Gallicchio et al.4 already gave a detailed decomposition of hydrophobic free energies into attractive and repulsive components by using an explicit solvent model and an OPLS all-atom force field. This allows a detailed comparison of our variational approach with other computational models. Using the optimized parameters, the results of 11 alkane compounds obtained from the present variational approach are shown in top section of Table 2. It is evident that our model reproduces the total solvation free energies of 11 alkanes very well. The present model accurately catches the subtle differences between linear, branched, and cyclic apolar compounds. The root mean square (RMS) error is found to be as small as 0.12 kcal/mol.
Table 2.
Numerical and experimental total solvation free energies for 30 alkane compounds. The numerical energy is the sum of the repulsive part and attractive part. The free parameters are chosen as γ = 0.0806 kcal/(mol Å2), p = 0.0191 kcal/(mol Å3), and kcal/mol.
| (kcal/mol) |
||||||
|---|---|---|---|---|---|---|
| Area | Volume | |||||
| Compound | (Å2) | (Å3) | Rep. part | Att. part | Numerical | Experimental1 |
| Methane | 50.78 | 32.27 | 4.71 | −2.73 | 1.98 | 2.00 |
| Ethane | 70.62 | 50.44 | 6.65 | −4.75 | 1.90 | 1.83 |
| Propane | 89.18 | 68.75 | 8.50 | −6.45 | 2.04 | 1.96 |
| Butane | 107.30 | 86.75 | 10.30 | −8.18 | 2.12 | 2.08 |
| Pentane | 126.49 | 105.01 | 12.19 | −9.82 | 2.37 | 2.33 |
| Hexane | 144.94 | 123.23 | 14.03 | −11.54 | 2.50 | 2.49 |
| Isobutane | 105.28 | 86.70 | 10.14 | −7.97 | 2.16 | 2.52 |
| 2-methylbutane | 120.68 | 104.89 | 11.73 | −9.35 | 2.38 | 2.38 |
| Neopentane | 121.83 | 104.48 | 11.81 | −9.20 | 2.61 | 2.50 |
| Cyclopentane | 109.70 | 92.55 | 10.60 | −9.43 | 1.17 | 1.20 |
| Cyclohexane | 123.64 | 109.69 | 12.05 | −10.78 | 1.27 | 1.23 |
| RMS of calibration set | 0.12 | |||||
| Octane | 181.89 | 159.30 | 17.70 | −14.94 | 2.77 | 2.89 |
| Heptane | 163.14 | 141.27 | 15.85 | −13.22 | 2.63 | 2.62 |
| Nonane | 200.46 | 177.25 | 19.54 | −16.59 | 2.95 | 3.14 |
| Decane | 218.96 | 195.28 | 21.38 | −18.41 | 2.97 | 3.16 |
| 2-methylpentane | 140.98 | 123.52 | 13.72 | −11.13 | 2.59 | 2.52 |
| 3-methylpropane | 139.79 | 123.33 | 13.62 | −11.01 | 2.61 | 2.51 |
| 3-methylhexane | 157.13 | 141.47 | 15.37 | −12.48 | 2.89 | 2.71 |
| 2-methylhexane | 157.84 | 140.78 | 15.41 | −12.72 | 2.69 | 2.93 |
| 3-methylpentane | 139.79 | 123.33 | 13.62 | −11.01 | 2.61 | 2.51 |
| 224-trimethylpentane | 165.05 | 157.86 | 16.32 | −13.20 | 3.12 | 2.87 |
| 22-dimethylbutane | 136.64 | 123.47 | 13.37 | −10.54 | 2.83 | 2.57 |
| 24-dimethylpentane | 150.90 | 139.16 | 14.82 | −12.13 | 2.70 | 2.87 |
| 22-dimethylpentane | 155.61 | 140.95 | 15.23 | −12.28 | 2.96 | 2.88 |
| 23-dimethylpentane | 153.36 | 141.02 | 15.05 | −12.10 | 2.96 | 2.52 |
| Cyclopropane | 81.50 | 62.11 | 7.76 | −6.38 | 1.38 | 0.75 |
| Cycloheptane | 137.19 | 127.16 | 13.49 | −12.10 | 1.39 | 0.80 |
| Cyclooctane | 150.46 | 144.47 | 14.89 | −13.28 | 1.61 | 0.86 |
| Methylcyclopentane | 126.98 | 110.56 | 12.35 | −10.91 | 1.44 | 1.60 |
| Methylcyclohexane | 140.72 | 127.39 | 13.78 | −12.20 | 1.57 | 1.61 |
| RMS of prediction set | 0.31 | |||||
Reference 58.
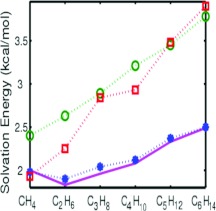
For a comparison, the results reported by Gallicchio et al.4 and Wagoner and Baker51 are also depicted in Fig. 3. Clearly, their models overestimate the solvation free energies of 11 alkane compounds. What is considered as a difficult task is the prediction of the check mark shape of the solvation free energies of the first six alkanes, i.e., a drop of the solvation free energy at ethane C2H6 before a monotonic increase of the solvation free energies as the alkanes increase in mass. It is noteworthy that the present variational approach correctly captures the check mark shape.
Figure 3.
Comparison of model predictions and experimental data58 of solvation free energies of six alkanesmethane, ethane, propane, butane, pentane, and hexane. Solid lines are for experimental data. Stars are for the numerical data obtained by the present variational approach. Squares are for the numerical data reported in Ref. 51. Circles are for the numerical data reported in Ref. 4.
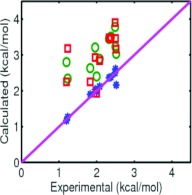
The repulsive and attractive parts of solvation free energies can be calculated separately in the present model. Such solvation decomposition results are also listed in Table 2. A comparison of the energies between the present variational approach and the explicit solvent model in Ref. 4 is given in Fig. 4. The present studies indicate that our variational approach performs better than an explicit solvent model4 in predicting the total solvation energy.
Figure 4.
Comparison of model predictions and experimental data58 of solvation free energies of eleven alkanes. Solid lines are for experimental data. Stars are for the numerical data obtained by the present variational approach. Squares are for the numerical data reported in Ref. 51. Circles are for the numerical data reported in Ref. 4.
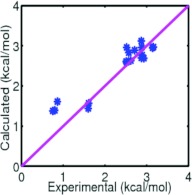
Having demonstrated the accuracy and reliability of our variational approach, we next conduct a predictive study of 19 other alkane compounds. This test set includes linear, branched, and cyclic apolar compounds. The same optimized parameters and computational procedure used for the above mentioned 11 alkane molecules are employed. Results are shown in the bottom section of Table 2, in which the repulsive and attractive decomposition is demonstrated as well. Our variational approach reproduces experimental results very well. The RMS error is 0.31 kcal/mol. Excellent agreement can be clearly seen in Fig. 5.
Figure 5.
Comparison of model predictions and experimental data of solvation free energies of nineteen alkanes.
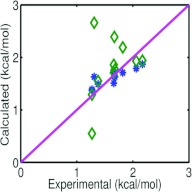
To further demonstrate the accuracy and reliability of the proposed variational approach, we finally consider calibration and prediction studies for a different type of apolar molecules, namely, alkenes. We employ a set of 11 alkene compounds which have been studied by Ratkova et al.61 using integral equation techniques. In the present study, we randomly choose a set of seven alkene compounds to train our model parameters, and then use them for the predictive study of the remaining four alkene molecules. Solvation free energies of 11 alkene compounds are shown in Table 3. The RMS errors for the calibration set and the prediction set are found to be, respectively, 0.177 kcal/mol and 0.180 kcal/mol. These RMS errors are significantly better than that reported in Ref. 61, which is about 0.462 kcal/mol, obtained by using the integral equation approach. This finding can be observed clearly from Fig. 6. In general, the present variational approach is simpler in theory and easier to implement than the integral equation approach.61
Table 3.
Numerical and experimental total solvation free energies for 11 alkenes. The numerical energy is the sum of the repulsive part and attractive part. The free parameters are chosen as γ = 0.0775 kcal/(mol Å2), p = 0.0192 kcal/(mol Å3), and kcal/mol.
| (kcal/mol) |
||||||
|---|---|---|---|---|---|---|
| Area | Volume | |||||
| Compound | (Å2) | (Å3) | Rep. part | Att. part | Numerical | Experimental1 |
| 3-methyl-1-butene | 121.37 | 101.51 | 11.34 | −9.63 | 1.71 | 1.82 |
| 1-butene | 103.99 | 83.30 | 9.65 | −8.16 | 1.49 | 1.38 |
| Ethene | 66.70 | 46.94 | 6.07 | −4.69 | 1.37 | 1.27 |
| 1-heptene | 160.72 | 137.95 | 15.09 | −13.33 | 1.76 | 1.66 |
| 1-hexene | 141.46 | 119.22 | 13.24 | −11.61 | 1.63 | 1.68 |
| 1-nonene | 197.53 | 173.23 | 18.62 | −16.82 | 1.79 | 2.06 |
| 2-methyl-2-butene | 120.55 | 101.33 | 11.28 | −9.65 | 1.63 | 1.31 |
| RMS of calibration set | 0.177 | |||||
| 1-octene | 179.23 | 156.17 | 16.87 | −15.00 | 1.87 | 2.17 |
| 1-pentene | 122.52 | 100.86 | 11.42 | −9.91 | 1.51 | 1.66 |
| 1-propene | 85.59 | 65.55 | 7.89 | −6.49 | 1.39 | 1.27 |
| Trans-2-heptene | 160.84 | 137.00 | 15.08 | −13.43 | 1.65 | 1.66 |
| RMS of prediction set | 0.180 | |||||
Figure 6.
Comparison of model predictions and experimental data58 of solvation free energies of eleven alkenes. In all charts, solid lines are for experimental data. Stars are for the numerical data obtained by the present variational approach. Diamonds are for the numerical data reported in Ref. 61.
CONCLUSION
In conclusion, this work provides a differential geometry based variational approach to improve the solvent-solute interface description in implicit solvent theory. This variational model offers increased accuracy and reliability in solvation free energy prediction, indicating the power of differential geometric methods for the analysis of solvation free energies. An implication of the present result is that the differential geometry based definition of solvent-solute boundaries is perhaps sufficient for solvation free energy predictions, although generalized correlations50 are needed in order to reproduce correct solvent microstructures.
ACKNOWLEDGMENTS
This work was supported in part by National Science Foundation (NSF) Grant Nos. CCF-0936830 and DMS-1160352, and National of Institutes of Health (NIH) Grant Nos. R01GM-090208 and GM069702. We thank the anonymous reviewers for useful suggestions.
References
- Ponder J. W. and Case D. A., “Force fields for protein simulations,” Adv. Protein Chem. 66, 27–85 (2003). 10.1016/S0065-3233(03)66002-X [DOI] [PubMed] [Google Scholar]
- Kamerlin S. C. L., Haranczyk M., and Warshel A., “Progress in ab initio QM/MM free-energy simulations of electrostatic energies in proteins: Accelerated QM/MM studies of pKa, redox reactions and solvation free energies,” J. Phys. Chem. B 113, 1253–1272 (2009). 10.1021/jp8071712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy R. M., Zhang L. Y., Gallicchio E., and Felts A. K., “On the nonpolar hydration free energy of proteins: surface area and continuum solvent models for the solute-solvent interaction energy,” J. Am. Chem. Soc. 125(31), 9523–9530 (2003). 10.1021/ja029833a [DOI] [PubMed] [Google Scholar]
- Gallicchio E., Kubo M. M., and Levy R. M., “Enthalpy-entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation,” J. Phys. Chem. B 104(26), 6271–6285 (2000). 10.1021/jp0006274 [DOI] [Google Scholar]
- Ishizuka R., Chong S. H., and Hirata F., “An integral equation theory for inhomogeneous molecular fluids: The reference interaction site model approach,” J. Chem. Phys. 128(3), 34504–34504 (2008). 10.1063/1.2819487 [DOI] [PubMed] [Google Scholar]
- Hsu C. S. and Chandler D., “Rism calculation of the structure of liquid acetonitrile,” Mol. Phys. 36(1), 215–224 (1978). 10.1080/00268977800101521 [DOI] [Google Scholar]
- Kovalenko A. and Hirata F., “Self-consistent description of a metal–water interface by the kohn–Sham density functional theory and the three-dimensional reference interaction site model,” J. Chem. Phys. 110, 10095 (1999). 10.1063/1.478883 [DOI] [Google Scholar]
- Lebowitz J. L. and Percus J. K., “Mean spherical model for lattice gases with extended hard cores and continuum fluids,” Phys. Rev. 144(1), 251 (1966). 10.1103/PhysRev.144.251 [DOI] [Google Scholar]
- Triolo R., Grigera J. R., and Blum L., “Simple electrolytes in the mean spherical approximation,” J. Phys. Chem. 80(17), 1858–1861 (1976). 10.1021/j100558a008 [DOI] [Google Scholar]
- Van Leeuwen J. M. J., Groeneveld J., and Boer J. De, “New method for the calculation of the pair correlation function. I,” Physica 25(7–12), 792–808 (1959). 10.1016/0031-8914(59)90004-7 [DOI] [Google Scholar]
- Ornstein L. S. and Zernike F., “Accidental deviations of density and opalescence at the critical point of a single substance,” Proc. R. Acad. Sci. Amsterdam 17, 793 (1914). [Google Scholar]
- Percus J. K., Frisch H. L., and Lebowitz J. L., The Equilibrium Theory of Classical Fluids, edited by Frisch H. L. and Lebowitz J. L. (Benjamin, 1964), p. 1133. [Google Scholar]
- Donley J. P., Curro J. G., and McCoy J. D., “A density functional theory for pair correlation functions in molecular liquids,” J. Chem. Phys. 101, 3205 (1994). 10.1063/1.467566 [DOI] [Google Scholar]
- Percus J. K. and Yevick G. J., “Analysis of classical statistical mechanics by means of collective coordinates,” Phys. Rev. 110(1), 1 (1958). 10.1103/PhysRev.110.1 [DOI] [Google Scholar]
- Wertheim M. S., “Exact solution of the Percus-Yevick integral equation for hard spheres,” Phys. Rev. Lett. 10(8), 321–323 (1963). 10.1103/PhysRevLett.10.321 [DOI] [Google Scholar]
- Koehl P., Orland H., and Delarue M., “Beyond Poisson-Boltzmann: Modeling biomolecule-water and water-water interactions,” Phys. Rev. Lett. 102(8), 087801 (2009). 10.1103/PhysRevLett.102.087801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassan S. A., “Liquid-structure forces and electrostatic modulation of biomolecular interactions in solution,” J. Phys. Chem. B 111(1), 227–241 (2007). 10.1021/jp0647479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinstein A. and Sherman S., “Evaluation of the influence of the internal aqueous solvent structure on electrostatic interactions at the protein-solvent interface by nonlocal continuum electrostatic approach,” Biopolymers 87(2-3), 149–164 (2007). 10.1002/bip.20808 [DOI] [PubMed] [Google Scholar]
- Madden P. and Kivelson D., A Consistent Molecular Treatment of Dielectric Phenomena, Advances in Chemical Physics Vol. 56, (1984), pp. 467–566.
- Sharp K. A. and Honig B., “Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equatlon,” J. Phys. Chem. 94, 7684–7692 (1990). 10.1021/j100382a068 [DOI] [Google Scholar]
- Gilson M. K., Davis M. E., Luty B. A., and McCammon J. A., “Computation of electrostatic forces on solvated molecules using the Poisson-Boltzmann equation,” J. Phys. Chem. 97(14), 3591–3600 (1993). 10.1021/j100116a025 [DOI] [PubMed] [Google Scholar]
- Stillinger F. H., “Structure in aqueous solutions of nonpolar solutes from the standpoint of scaled-particle theory,” J. Solution Chem. 2, 141–158 (1973). 10.1007/BF00651970 [DOI] [Google Scholar]
- Dong F., Wagoner J. A., and Baker N. A., “Assessing the performance of implicit solvation models at a nucleic acid surface,” Phys. Chem. Chem. Phys. 10, 4889–4902 (2008). 10.1039/b807384h [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cramer C. J. and Truhlar D. G., “Implicit solvation models: Equilibria, structure, spectra, and dynamics,” Chem. Rev. 99, 2161–2200 (1999). 10.1021/cr960149m [DOI] [PubMed] [Google Scholar]
- Husowitz B. and Talanquer V., “Solvent density inhomogeneities and solvation free energies in supercritical diatomic fluids: A density functional approach,” J. Chem. Phys. 126(5), 054508 (2007). 10.1063/1.2432327 [DOI] [PubMed] [Google Scholar]
- Reddy M. R., Singh U. C., and Erion M. D., “Ab initio quantum mechanics-based free energy perturbation method for calculating relative solvation free energies,” J. Comput. Chem. 28(2), 491–494 (2007). 10.1002/jcc.20510 [DOI] [PubMed] [Google Scholar]
- Marenich A. V., Cramer C. J., and Truhlar D. G., “Perspective on foundations of solvation modeling: The electrostatic contribution to the free energy of solvation,” J. Chem. Theory Comput. 4(6), 877–887 (2008). 10.1021/ct800029c [DOI] [PubMed] [Google Scholar]
- Rocchia W., Sridharan S., Nicholls A., Alexov E., Chiabrera A., and Honig B., “Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects,” J. Comput. Chem. 23, 128–137 (2002). 10.1002/jcc.1161 [DOI] [PubMed] [Google Scholar]
- Lee B. and Richards F. M., “The interpretation of protein structures: Estimation of static accessibility,” J. Mol. Biol. 55(3), 379–400 (1971). 10.1016/0022-2836(71)90324-X [DOI] [PubMed] [Google Scholar]
- Richards F. M., “Areas, volumes, packing, and protein structure,” Annu. Rev. Biophys. Bioeng. 6(1), 151–176 (1977). 10.1146/annurev.bb.06.060177.001055 [DOI] [PubMed] [Google Scholar]
- Spolar R. S., Ha J. H., and M. T.RecordJr., “Hydrophobic effect in protein folding and other noncovalent processes involving proteins,” Proc. Natl. Acad. Sci. U.S.A. 86(21), 8382–8385 (1989). 10.1073/pnas.86.21.8382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingstone J. R., Spolar R. S., and M. T.RecordJr., “Contribution to the thermodynamics of protein folding from the reduction in water-accessible nonpolar surface area,” Biochemistry 30(17), 4237–4244 (1991). 10.1021/bi00231a019 [DOI] [PubMed] [Google Scholar]
- Crowley P. B. and Golovin A., “Cation-π interactions in protein-protein interfaces,” Proteins: Struct., Funct., Bioinf. 59(2), 231–239 (2005). 10.1002/prot.20417 [DOI] [PubMed] [Google Scholar]
- Kuhn L. A., Siani M. A., Pique M. E., Fisher C. L., Getzoff E. D., and Tainer J. A., “The interdependence of protein surface topography and bound water molecules revealed by surface accessibility and fractal density measures,” J. Mol. Biol. 228(1), 13–22 (1992). 10.1016/0022-2836(92)90487-5 [DOI] [PubMed] [Google Scholar]
- Bergstrom C. A. S., Strafford M., Lazorova L., Avdeef A., Luthman K., and Artursson P., “Absorption classification of oral drugs based on molecular surface properties,” J. Med. Chem. 46(4), 558–570 (2003). 10.1021/jm020986i [DOI] [PubMed] [Google Scholar]
- Dragan A. I., Read C. M., Makeyeva E. N., Milgotina E. I., Churchill M. E., Crane-Robinson C., and Privalov P. L., “DNA binding and bending by HMG boxes: Energetic determinants of specificity,” J. Mol. Biol. 343(2), 371–393 (2004). 10.1016/j.jmb.2004.08.035 [DOI] [PubMed] [Google Scholar]
- Jackson R. M. and Sternberg M. J., “A continuum model for protein-protein interactions: Application to the docking problem,” J. Mol. Biol. 250(2), 258–275 (1995). 10.1006/jmbi.1995.0375 [DOI] [PubMed] [Google Scholar]
- Licata V. J. and Allewell N. M., “Functionally linked hydration changes in Escherichia coli aspartate transcarbamylase and its catalytic subunit,” Biochemistry 36(33), 10161–10167 (1997). 10.1021/bi970669r [DOI] [PubMed] [Google Scholar]
- Sanner M. F., Olson A. J., and Spehner J. C., “Reduced surface: An efficient way to compute molecular surfaces,” Biopolymers 38, 305–320 (1996). [DOI] [PubMed] [Google Scholar]
- Wei G. W., Sun Y. H., Zhou Y. C., and Feig M., “Molecular multiresolution surfaces,” e-print arXiv:math-ph/0511001v1.
- Bates P. W., Wei G. W., and Zhao S., “The minimal molecular surface,” e-print arXiv:q-bio/0610038v1 [q-bio.BM].
- Bates P. W., Wei G. W., and Zhao S., “Minimal molecular surfaces and their applications,” J. Comput. Chem. 29(3), 380–391 (2008). 10.1002/jcc.20796 [DOI] [PubMed] [Google Scholar]
- Bates P. W., Chen Z., Sun Y. H., Wei G. W., and Zhao S., “Geometric and potential driving formation and evolution of biomolecular surfaces,” J. Math. Biol. 59, 193–231 (2009). 10.1007/s00285-008-0226-7 [DOI] [PubMed] [Google Scholar]
- Wei G. W., “Differential geometry based multiscale models,” Bull. Math. Biol. 72, 1562–1622 (2010). 10.1007/s11538-010-9511-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z., Baker N. A., and Wei G. W., “Differential geometry based solvation models I: Eulerian formulation,” J. Comput. Phys. 229, 8231–8258 (2010). 10.1016/j.jcp.2010.06.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z., Baker N. A., and Wei G. W., “Differential geometry based solvation models II: Lagrangian formulation,” J. Math. Biol. 63, 1139–1200 (2011). 10.1007/s00285-011-0402-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z. and Wei G. W., “Differential geometry based solvation model. III. Quantum formulation,” J. Chem. Phys. 135, 194108 (2011). 10.1063/1.3660212 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dzubiella J., Swanson J. M. J., and McCammon J. A., “Coupling hydrophobicity, dispersion, and electrostatics in continuum solvent models,” Phys. Rev. Lett. 96, 087802 (2006). 10.1103/PhysRevLett.96.087802 [DOI] [PubMed] [Google Scholar]
- Cheng L. T., Dzubiella J., McCammon J. A., and Li B., “Application of the level-set method to the implicit solvation of nonpolar molecules,” J. Chem. Phys. 127(8), 084503 (2007). 10.1063/1.2757169 [DOI] [PubMed] [Google Scholar]
- Wei G.-W., Zheng Q., Chen Z., and Xia K., “Variational multiscale models for charge transport,” SIAM Rev. (to be published). [DOI] [PMC free article] [PubMed]
- Wagoner J. A. and Baker N. A., “Assessing implicit models for nonpolar mean solvation forces: the importance of dispersion and volume terms,” Proc. Natl. Acad. Sci. U.S.A. 103(22), 8331–8336 (2006). 10.1073/pnas.0600118103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E., Zhang L. Y., and Levy R. M., “The SGB/NP hydration free energy model based on the surface generalized Born solvent reaction field and novel nonpolar hydration free energy estimators,” J. Comput. Chem. 23(5), 517–529 (2002). 10.1002/jcc.10045 [DOI] [PubMed] [Google Scholar]
- Gallicchio E. and Levy R. M., “AGBNP: An analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling,” J. Comput. Chem. 25(4), 479–499 (2004). 10.1002/jcc.10400 [DOI] [PubMed] [Google Scholar]
- Weeks J. D., Chandler D., and Andersen H. C., “Role of repulsive forces in determining the equilibrium structure of simple liquids,” J. Chem. Phys. 54(12), 5237–5247 (1971). 10.1063/1.1674820 [DOI] [Google Scholar]
- Nicholls A., Mobley D. L., Guthrie P. J., Chodera J. D., and Pande V. S., “Predicting small-molecule solvation free energies: An informal blind test for computational chemistry,” J. Med. Chem. 51(4), 769–779 (2008). 10.1021/jm070549+ [DOI] [PubMed] [Google Scholar]
- Lorensen W. E. and Cline H. E., “Marching cubes: A high resolution 3D surface reconstruction algorithm,” Comput. Graphics 21, 163–169 (1987). 10.1145/37402.37422 [DOI] [Google Scholar]
- Geng W. H. and Wei G. W., “Multiscale molecular dynamics via the matched interface and boundary (mib) method,” J. Comput. Phys. 230, 435–457 (2011). 10.1016/j.jcp.2010.09.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabani S., Gianni P., Mollica V., and Lepori L., “Group contributions to the thermodynamic properties of non-ionic organic solutes in dilute aqueous solution,” J. Solution Chem. 10(8), 563–595 (1981). 10.1007/BF00646936 [DOI] [Google Scholar]
- Perlman D. A., Case D. A., Caldwell J. W., Ross W. S., Cheatham T. E., Debolt S., Ferguson D., Seibel G., and Kollman P., “AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules,” Comput. Phys. Commun. 91, 1–41 (1995). 10.1016/0010-4655(95)00041-D [DOI] [Google Scholar]
- Veenstra D., Ferguson D., and Kollman P., “How transferable are hydrogen parameters in molecular mechanics calculations?,” J. Comput. Chem. 13(8), 971–978 (1992). 10.1002/jcc.540130807 [DOI] [Google Scholar]
- Ratkova E. L., Chuev G. N., Sergiievskyi V. P., and Fedorov M. V., “An accurate prediction of hydration free energies by combination of molecular integral equations theory with structural descriptors,” J. Phys. Chem. B 114(37), 12068–12079 (2010). 10.1021/jp103955r [DOI] [PubMed] [Google Scholar]