Figure 4.
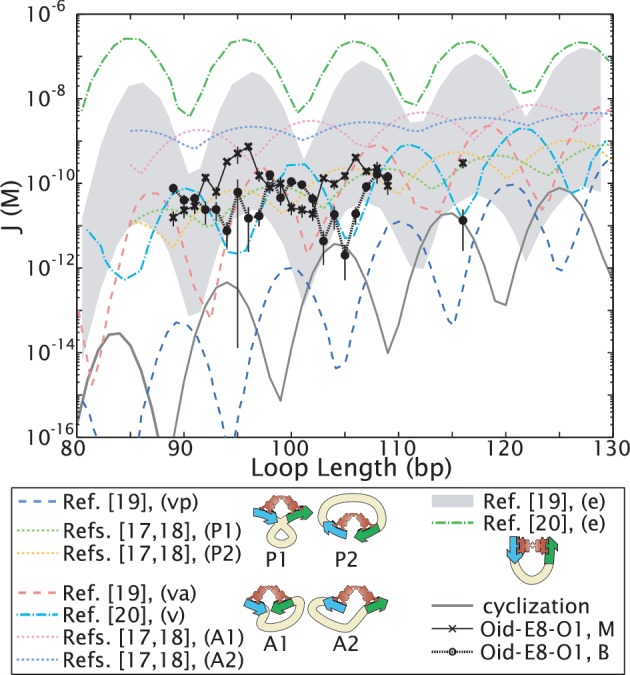
Theoretical predictions of the length dependence of the looping J-factor demonstrate that different assumptions about loop conformation and/or protein flexibility lead to predicted looping J-factors that can differ by orders of magnitude. Elasticity theory with ‘canonical’ values for the stiffness of random DNA sequences, in conjunction with various models of the geometric and mechanical constraints imposed by the Lac repressor tetramer, have been used to compute the looping J-factor (17–20). The model of (17,18) also explicitly includes the boundary conditions of a TPM experiment, with a bead on one end of the DNA and a surface on the other. The assumed constraints can be roughly grouped into V-like repressor conformations, similar to the shape seen in the crystal structure 1LBI (47) [‘P1’ and ‘P2,’ indistinguishable unless as in TPM there are symmetry-breaking boundary conditions, and therefore collapsed into one state, ‘vp,’ in (19); and ‘A1’ and ‘A2,’ collapsed into ‘v’ or ‘va’ in (19,20)]; and more extended repressor conformations (‘e’), which are favored by the DNA mechanics. These conformations are indicated schematically in the legend; for the case of (17,18), the blue operator has been chosen to be Oid, that is, the operator closest to the surface. The prediction for the extended conformation of (19) is a range of values, reflecting estimated uncertainty in the free energy costs of opening the repressor tetramer. Details of how these curves were obtained are given in Section S2 in the Supplementary Data. Our experimental measurements for the two looped states of the no-promoter E8 sequence (‘Oid-E8-O1, M’ and ‘Oid-E8-O1, B,’) as well as the cyclization result of Shimada and Yamakawa (16,17) (‘cyclization’) have been included for comparison.
