Expectation-Maximization Algorithm for Determining Natural Selection of Y-Linked Genes Through Two-Sex Branching Processes

Abstract

A two-dimensional bisexual branching process has recently been presented for the analysis of the generation-to-generation evolution of the number of carriers of a Y-linked gene. In this model, preference of females for males with a specific genetic characteristic is assumed to be determined by an allele of the gene. It has been shown that the behavior of this kind of Y-linked gene is strongly related to the reproduction law of each genotype. In practice, the corresponding offspring distributions are usually unknown, and it is necessary to develop their estimation theory in order to determine the natural selection of the gene. Here we deal with the estimation problem for the offspring distribution of each genotype of a Y-linked gene when the only observable data are each generation's total numbers of males of each genotype and of females. We set out the problem in a non parametric framework and obtain the maximum likelihood estimators of the offspring distributions using an expectation-maximization algorithm. From these estimators, we also derive the estimators for the reproduction mean of each genotype and forecast the distribution of the future population sizes. Finally, we check the accuracy of the algorithm by means of a simulation study.

1. Introduction

Recent research has shown the importance of certain genes linked to the Y chromosome in populations of humans (Hughes et al., 2005) and other animals (Charlesworth et al., 2005). This chromosome has the particularity of being male-specific (the SRY gene is responsible for maleness) and haploid, and of having a region that escapes recombination (the nonrecombining region, NRY, which is 95% of the chromosome in humans—see, for example, Graves, 2006). The unique properties of the Y chromosome have major consequences for its population genetics: The NRY region passes down from father to son largely unchanged, preserving the paternal genetic legacy, and is therefore very useful for studying how populations have evolved. A history of paternal lineages can be reproduced by examining the differences (such as DNA polymorphisms) among modern Y chromosomes. There have been many studies in this sense in the context of populations of humans (e.g., The Y Chromosome Consortium studies or Rosa et al., 2007) and other species (Hellborg et al., 2005). In human populations, the surname can also be regarded as a Y-linked characteristic, and there have been studies aimed at determining its relationship with Y-chromosome lineages (King et al., 2006).

Another singular question associated with the Y chromosome is that of the microdeletions of this chromosome's long arm (Yq). The Yq deletion is associated with males who have fertility problems (Krausz et al., 2003), but many cases have been reported in which the natural transmission of this genetic defect from fathers to sons has occurred (Kuhnert et al., 2004). Obviously, determining the evolution of the number of males with this genetic defect in a human population is an important medical problem (Fitch et al., 2005), but it has also been investigated in other species (Toure et al., 2004). Moreover, there is evidence that the Y chromosome plays a role in skeletal growth, germ-cell tumorigenesis, and graft rejection, and that its genes might also influence gender-specific differences in disease susceptibility.

Appropriate mathematical models are needed to understand the evolution of Y chromosome lineages (for instance, to help solve the problem of Y-chromosomal Adam—the theoretical male who is the most recent common patrilineal ancestor of all living humans; estimations of the date of this common ancestor is an important problem), Yq deletions, or other Y-linked genes.

Many models used in population genetics are based on the Wright-Fisher model, although branching processes naturally come to mind in this context and represent a clear alternative approach. These processes are stochastic models, which arise in the description of population dynamics, being of particular use in describing the extinction/growth of populations (Haccou et al., 2005). Branching models have been applied to many biological problems in such fields as epidemiology, genetics, and cell kinetics. Examples include the evolution of infectious diseases (Garske and Rhodes, 2008), population genetics (Iwasa et al., 2005), and stem cells (Yakovlev and Yanev 2006). Further examples are reviewed in the recent monographs of Kimmel and Axelrod (2002), Pakes (2003), and González et al. (2010). A comparison between Wright-Fisher and branching models can be found in the recent article of Cyran and Kimmel (2010).

The simplest branching models are the Galton-Watson and the Markov branching processes. They have been used to model Y-chromosome lineages and their female analogues—mitochondrial DNA lineages (Neves and Moreira, 2006; Cyran and Kimmel, 2010). But more accurate models are needed in which all the phases of sexual reproduction can be considered, including the interaction between females and males in producing offspring. Recently, two models (González et al., 2006; González et al., 2009b) have been presented to describe the evolution of the number of carriers of the two alleles of a Y-linked gene (so that there are two types of male, each carrying one of these alleles) in a two-sex monogamic population. In the first, it was considered that the characters controlled by such a gene can influence the mating process of the species, with females having a preference for males carrying one of the alleles of the gene (Pidancier et al., 2006). It was shown (González et al., 2008) that this preference can sometimes be definitive in determining the survival of the different genotypes in the population. This model was denominated a Y-linked bisexual branching process (Y-linked BBP) with preference. And in the second, González et al. (2009b), it was considered that females choose their mates without caring about their genotype that is, each female makes a blind choice of the genotype of her mate. This model was called Y-linked BBP with blind choice.

The focus of the present article is the first model, a Y-linked BBP with preference, to pattern the evolution of the number of carriers of each allele of a Y-linked gene or of Y chromosome lineages in a two-sex monogamic population, assuming that this gene influences the mating process. In González et al. (2006) and González et al. (2008), it was shown that the behavior of genes that fit the pattern of a Y-linked BBP with preference is strongly related to the reproduction laws of each genotype, that is, those that model natural selection. In practice, these offspring distributions are usually unknown and need to be estimated to guarantee the applicability of these models. In this article, we deal with the problem of estimating the offspring distribution of each genotype of a Y-linked gene (as well as some related parameters, such as their mean values and future population sizes). We consider a frequentist and nonparametric framework.

First, we obtain the maximum likelihood estimators (MLEs) of the parameters when the complete family tree is observed up to some fixed generation. The limiting behavior (consistency and asymptotic normality) of these estimators is also studied. Since it is usually impossible in practice to observe the entire family tree, we then consider the problem of estimating the main parameters of the model, using only the sample given by the numbers of females and of the two different types of male in each generation, which are more easily observed. We approach this problem as an incomplete data estimation problem. This leads us to apply an expectation-maximization (EM) algorithm (McLachlan and Krishnan, 2008) in order to obtain the MLEs. (For a review on the use of this kind of algorithm in genetics see Laird, 2010).

Besides the Introduction, this article consists of four additional sections. In Section 2, we provide the definition of the Y-linked BBP with preference. In Section 3, we obtain the MLEs, assuming the complete and incomplete sampling schemes indicated above, and present the development of the EM algorithm. The accuracy of this algorithm is illustrated in Section 4 by means of a simulated example (figures are included as Supplementary Material, available online at www.liebertpub.com/cmb). Some concluding remarks are provided in Section 5. Finally, the proofs of some theoretical results related to the asymptotic properties of the MLEs based on the complete family tree sample are shown in the Supplementary Material.

2. The probability model

The probability model we deal with is the Y-linked BBP with preference that was introduced in González et al. (2006). This model describes the evolution of the number of carriers of a Y-linked gene generation-by-generation. It is assumed that the gene has a pair of alleles, denoted by R and r, which are expressed in the male phenotype (r can model the absence of R). We are thus assuming a population formed by females and males, where two types of male can be observed depending on the allele they carry. Males with R allele are denoted R males, while males with r allele are denoted r males. Hence, two types of (male–female) couple are formed—those consisting of one female and one R male (resp. r male) are denoted R (resp. r) couples.

Assuming nonoverlapping generations, and having fixed the number of couples of each type at the initial (n = 0) generation, the population size is determined in each generation according to two phases: reproduction and mating. In the reproduction phase, each couple is assumed to randomly produce offspring independently of the other couples. The probability distributions of these variables are the same for all the couples with a given genotype. Moreover, following the inheritance rules, R couples can generate females and R males, while r couples can generate females and r males (no mutation is assumed). More formally, we consider two independent sequences

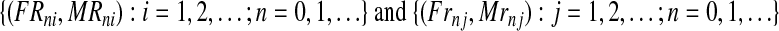of independent, identically distributed, non-negative and integer-valued bivariate random vectors, where (FR_ni, MR_ni) (resp. (Fr_nj, Mr_nj)) represents the number of females and males generated by the i-th R couple (resp. j-th r couple) in generation n.

In general, (FR_ni, MR_ni) and (Fr_nj, Mr_nj) may have different distributions, modeling the natural selection between genotypes (i.e., their possibly different reproductive abilities). In particular, the total number of offspring generated by an R couple (resp. r couple) is specified by a probability distribution 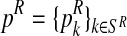(resp. 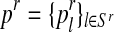), where , with S^R (resp. S^r) being the support of the distribution that is considered finite. This probability distribution is called the reproduction law of the R genotype (resp. r genotype). Moreover, we denote by m_R (resp. m_r) the average number of offspring per R couple (resp. r couple).

In order to model the sex designation, we consider that each offspring will be female with probability α, 0 < α < 1, or male with probability 1 − α (i.e., a binomial reproduction scheme). These sex designations are made independently among the offspring of any couple, and it is assumed that the genotype has no influence on sex determination, so that α is the same for both genotypes. Then, given an R couple (resp. r couple) that has produced k (resp. l) offspring, the number of females among these—i.e., FR_ni (resp. Fr_nj)—follows a binomial distribution of size k (resp. l) and probability α. Hence, the average number of females and males per R couple (resp. r couple) is, respectively, αm_R and (1 − α)m_R (resp. αm_r and (1 − α)m_r).

Therefore, for a generation n with total numbers of R and r couples ZR_n and Zr_n, respectively, one obtains the total number of females in generation n + 1, as well as the number of males stemming from R couples (resp. r couples) in generation n + 1,

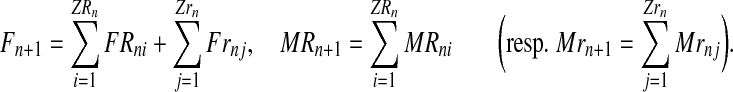(1)

Once the total numbers of females and males of each type in generation (n + 1) are known (i.e., F_n+1,MR_n+1, and Mr_n+1), one deals with the mating phase. To determine the total number of couples of each type, we assume perfect fidelity mating (i.e., each individual mates with only one individual of the other sex provided that some of them are still available), and also that females choose their partner with a preference for R males. Hence, R males are chosen first, so the total number of R couples is determined by the minimum of the number of females and the number of R males:

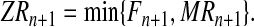(2)

Therefore, the number of females that do not mate with R males is max{0,F_n+1 -MR_n+1}. These females (if any) mate with r males, and the assumption of perfect fidelity implies that the number of r couples is

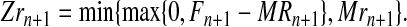(3)

Notice that the number of couples of each type in the (n + 1)-th generation is given deterministically once the total numbers of females and of males of each type in this generation are known.

From the definition of the model, the number of couples of each genotype in the next generation depends only on the present number of mating units and not on the number of ancestors that belonged to past generations. Furthermore, since each reproduction law remains the same over the generations, the transitions from one generation to another are homogeneous. The process {(ZR_n, Zr_n)}_n≥0 is therefore a homogeneous two-type Markov chain.

Some basic properties of this model are established in González et al. (2006). Among them, particularly worthy of note is that each genotype presents the dual behavior typical of branching processes: either it becomes extinct or the number of couples of this genotype eventually reaches arbitrarily large values. The latter event is known as the explosion or indefinite growth of this particular genotype. Consequently, the whole population also presents this duality. Although this property might seem unrealistic, it merely expresses what would be the ideal long-term evolution of a population when its development is not constrained by any external bound.

In González et al. (2009a), conditions for the survival/fixation of one genotype and the extinction/survival of the whole population are reviewed. These conditions depend on α and on the reproduction laws p^R and p^r through their mean values m_R and m_r, respectively. These values also determine the asymptotic behavior of the genotypes (as was proved in González et al., 2008). Since in practice these parameters are usually unknown, in order for these models to be applicable it is necessary to develop the estimation theory for the above parameters, including the reproduction laws. Then, knowing these estimators, predictions about the number of individuals and couples in future generations can also be established.

3. Maximum likelihood estimators with complete and incomplete data

In this section, we shall study the MLEs of the parameters α, p^R, and p^r. We shall also derive from them the MLEs for the reproduction means m_R and m_r. First we consider that the entire family tree up to some generation N is observed. This is the set of random vectors

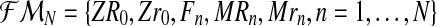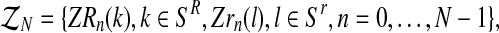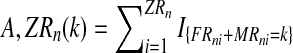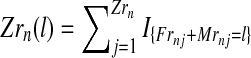From these random vectors, assuming that (ZR₀, Zr₀) is known and using Equations (1)–(3), one can obtain the sets , containing the initial number of couples of each type and the total number of females and the total number of males of each type until generation N; and where, with I_A denoting the indicator function of the set and represent the total number of couples of each type that have generated, respectively, k and l individuals in the generation n.

Therefore, taking into account the binomial scheme and that mating units reproduce independently, it is not hard to obtain that the complete likelihood function based on the sample 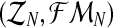is given by

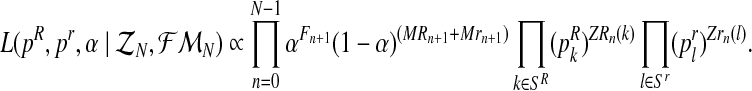(4)

From this expression, and adapting some classical procedures of estimation theory in branching processes (see Supplementary Material, Theorem 1), one can obtain that the MLEs for α, p^R, and p^r based on the sample 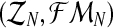are given by

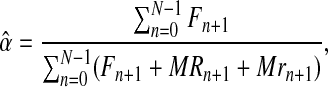(5)

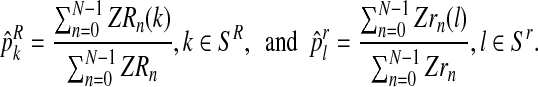The estimator for α is intuitively very reasonable, since it is obtained by means of the proportion of females among all observed individuals. The estimator for 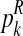with 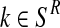(resp. 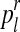with 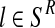) is obtained as the total number of R couples (resp. r couples) that have generated k (resp. l) offspring as a fraction of the total number of R couples (resp. r couples).

From the estimators of p^R and p^r, one deduces that the MLEs for m_R and m_r based on the sampl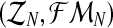e are

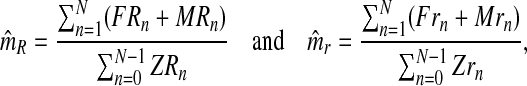where 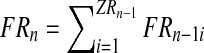and 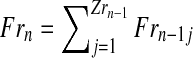, for all 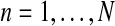, are the total numbers of females generated by each type of couple. Notice that for 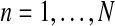, FR_n and Fr_n are derived from 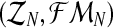, since 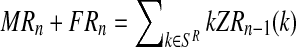and .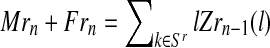

All of these estimators verify some properties related to their asymptotic behavior. Specifically, on the nonextinction set, each estimator is strongly consistent, and, suitably normalized, converges in distribution to a standard normal distribution (see Supplementary Material).

Notice that the above estimators depend on the sample 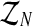which, in most real situations, is impossible to observe. Usually, only the total number of individuals of each type can be observed (recall that the Y-linked genes present different phenotypes). Thus, there arises an interesting estimation problem from assuming that only the sample 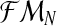is observed. Since, from the definition of the model [Eq. (2) and (3)], one obtains ZR_n and Zr_n deterministically, knowing the total number of females and the total numbers of males of each type, one can insert the variables ZR_n and Zr_n into the sample 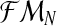. Hence, writing 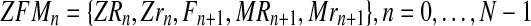, one is considering that the sample observed is .

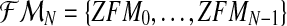Assuming that 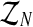is unknown and only the total number of individuals and of couples are observed, one is faced with an incomplete data estimation problem. In such a case, it seems appropriate to use an expectation-maximization (EM) algorithm (McLachlan and Krishnan, 2008), extensively used to deal with maximum likelihood calculations when there are missing or incomplete data. This algorithm is an iterative method that consists of two steps. In the first step (E step), the expectation of the complete log-likelihood is calculated using the distribution of the unobserved data. The second step (M step) consists of finding the values of the parameters that maximize the expectation that had been calculated in the E step. The E and M steps are repeated until convergence is attained. In our case, starting with initial values (p^R(0), p^r(0), α⁽⁰⁾), we shall obtain a sequence {(p^R(i), p^r(i), α⁽ⁱ⁾)}_i≥0 that is updated in each iteration of the method, as will be described in the following section.

3.1. The E step

Let (p^R(i), p^r(i), α⁽ⁱ⁾) be the vector obtained in iteration i (where 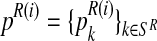and 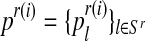). We shall develop the E step of the EM algorithm in the (i + 1)-th iteration. The expected value of the complete log-likelihood with respect to the available data 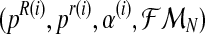is given by the expression

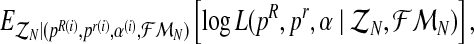(6)

where 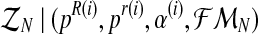denotes the distribution of the latent vector 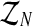, given the sample 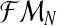and the parameters of the model (p^R(i),p^r(i),α⁽ⁱ⁾). For simplicity, we shall henceforth write 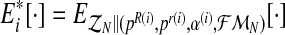. Taking into account Equation (4), one has

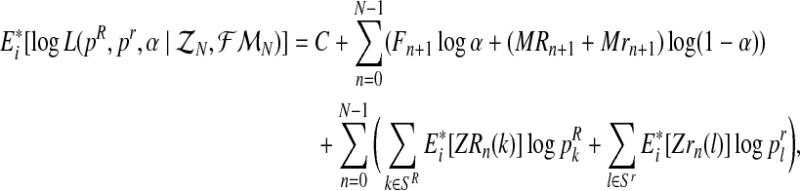for a certain constant C.

Therefore, in order to obtain the expected value of the complete log-likelihood, the distribution of the unobserved data 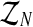with respect to 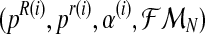needs to be calculated. To determine the distribution of 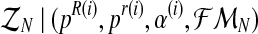, we must first show the relationship between the vectors and 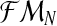. Indeed, since the sum, for all 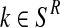(resp. 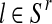); of the total number of R couples that have generated k (resp. l) offspring is the total number of R couples (resp. r couples), then

(7)

The total number of individuals generated by the R couples (resp. r couples) is greater than or equal to the total number of R males (resp. r males) generated by these couples, that is,

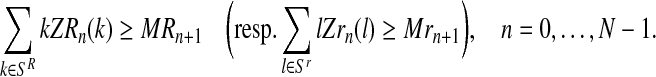(8)

Also, the total number of individuals generated by all couples in a generation is the sum total of the number of individuals of the next generation:

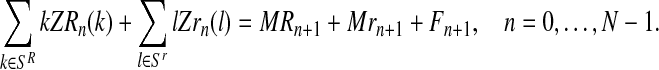(9)

Considering these relationships, we can now determine the distribution of the unobserved vector 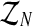, given 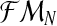and the vector of i-th iteration values (p^R(i), p^r(i), α⁽ⁱ⁾). To this end, let us denote by fm_N a vector of non-negative integers, , where, for all 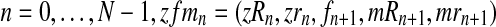. In order for fm_N to be a possible value of 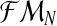, and according to the definition of the model, we assume that zR_n+1 = min{f_n+1,mR_n+1} and 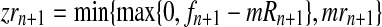, for 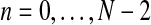, [see Eqs. (2) and (3)]. One then has that, almost surely,

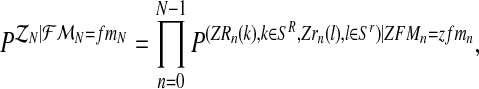(10)

where 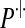denotes the conditional distribution with parameters (p^R(i), p^r(i), α⁽ⁱ⁾). Indeed, denote by z_N a vector of non-negative integers with 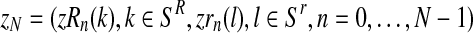, and, for each 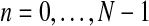, write the sets

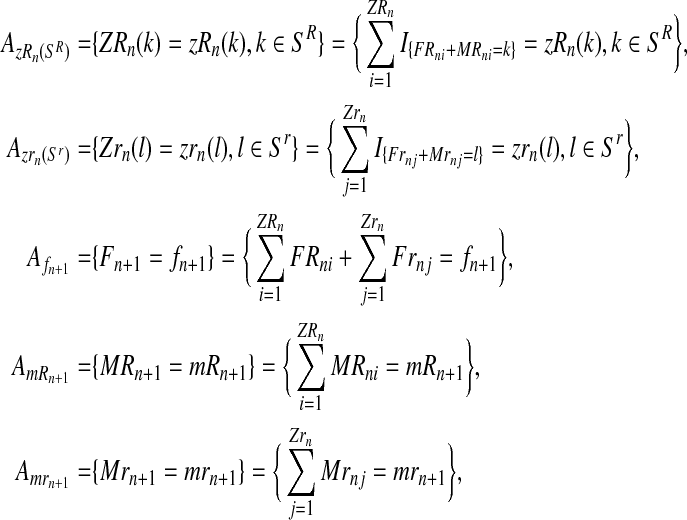with 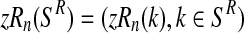and 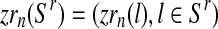. Then, since mating units reproduce independently, one has that

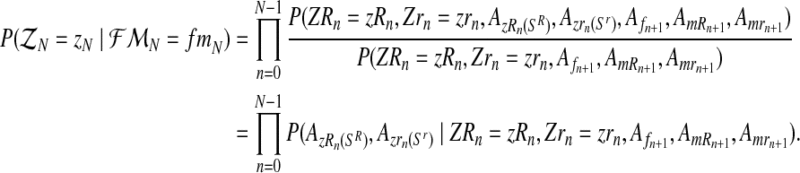Computationally, this means that the vector 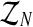can be determined generation-by-generation. Specifically, once the total numbers are known of couples of each type in the n-th generation, ZR_n and Zr_n, and of females and of males of each type in the (n + 1)-th generation, F_n+1, MR_n+1, and Mr_n+1, it is enough to sample the vector 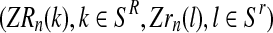in the following way. Applying the multiplication rule, one straightforwardly obtains that the probability 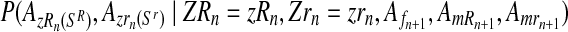is proportional to the product of the probabilities

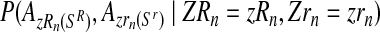(11)

and

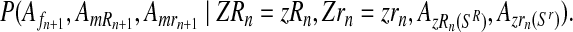(12)

Taking into account that mating units reproduce independently, the probability given in Equation (11) is obtained as .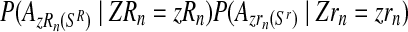

Since 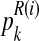(resp. 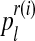) is considered to be the probability that an R couple (resp. r couple) generates k (resp. l) offspring and there are zR_n (resp. zr_n) progenitor couples, then, taking into account Equation (7), one deduces that 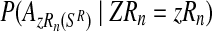(resp. 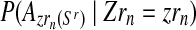is obtained from a multinomial distribution with size zR_n (resp. zr_n) and probability p^R(i) (resp. p^r(i)) if 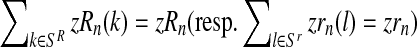), or is equal to 0 otherwise.

The probability given in Equation (12), from again applying the multiplication rule, is proportional to the product of the probabilities

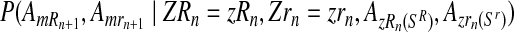(13)

and

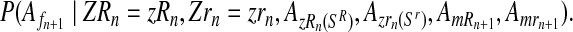(14)

Considering Equation (9), the probability given in Equation (14) is equal to 1 if 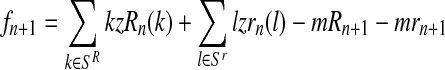, or to 0 otherwise.

Finally, given that the sex designations are made independently among the offspring and that mating units reproduce independently, the probability given in Equation (13) is equal to the product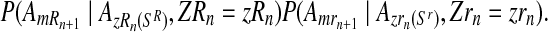

Moreover, taking into account Equation (8) and the binomial scheme, the first (resp. second) probability is obtained from a binomial distribution with size 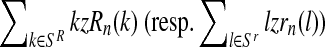and probability 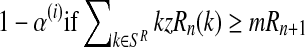(resp. 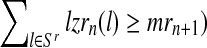, that is, if the total number of offspring given by all mating units of a type is greater than the total number of males of this type; otherwise, it is equal to 0.

3.2. The M Step

The M step consists of finding the values of the parameters that maximize the expectation of the complete log-likelihood. This expectation has been calculated previously in the E step. In our case, we must find the vector (p^R(i+1), p^r(i+1), α⁽ⁱ⁺¹⁾) that maximizes the expression 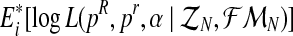. Following a similar argument to that given in the calculation of the MLEs, based on the observation of the complete family tree (see Supplementary Material, Theorem 1), one obtains that the value for α in the (i + 1)-th iteration is

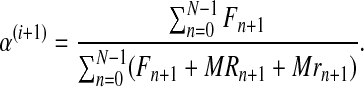Notice that α⁽ⁱ⁺¹⁾ does not depend on the iteration i because it is only based on 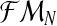, which is observed. The sequence 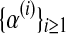is thus constant in all iterations of the method, and its value will be denoted 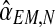. This value coincides with the MLE given in Equation (5) based on observing the entire family tree.

For eac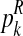h with 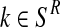and each 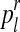with 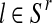, the values obtained in the (i + 1)-th iteration are, respectively,

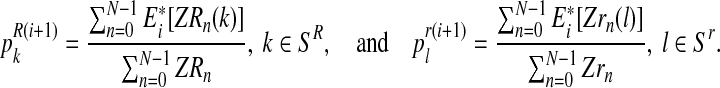Intuitively, 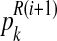(resp. 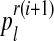) is the ratio of the average number of R couples (resp. r couples) that have generated k (resp. l) offspring to the total number of R couples (resp. r couples). To calculate these average numbers, one has to use the probability distribution determined in E step.

The values obtained in this M step, 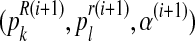, are used to begin another E step, and the process is repeated until some convergence criterion is verified, in which case the process stops and the final values are denoted by 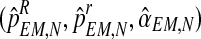. For simplicity, when the meaning is clear, we shall drop the use of the subindex N and write simply . In McLachlan and Krishnan (2008), it is shown that, under general conditions of differentiability and continuity of the expectation of the complete log-likelihood function, estimates obtained using the EM algorithm converge to a stationary point of the incomplete data likelihood function. The multinomial structure of our complete likelihood function means that usually those conditions are verified, and also that the incomplete data likelihood function is unimodal. Then, in this case, 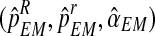are the MLEs of (p^R, p^r, α) based on , which we call expectation-maximization MLEs.

Remark 1

Another general scenario that can be considered is to observe only the number of couples of each type up to generation N, i.e., 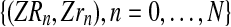. However, in this situation, the parameter α often can not be estimated using the EM algorithm, because the incomplete data likelihood function is not unimodal. For instance, if one has a Y-linked BBP with preference where 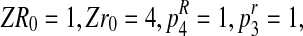ZR₁=2, and Zr₁ = 3, then the total number of individuals from R couples in the 1^st generation is equal to 4. Since Zr₁ is not null and ZR₁ = 2, there are two R males and thus there are also two females stemming from R couples, which form two mating couples. Moreover, since Zr₀ = 4 and , the total number of individuals from r couples in the 1^st generation is 12, of which 3 are females and 9 males or vice versa, because Zr₁ = 3. Thus, the incomplete data likelihood function is proportional to α⁵(1 − α)¹¹ + α¹¹(1 − α)⁵ (symmetric form), which is bimodal, so that the EM algorithm does not work correctly.

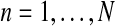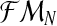Hence, to estimate α correctly, it would be necessary to also observe F_n and M_n, , with M_n = MR_n + Mr_n. In general these last variables, together with ZR_n and Zr_n, , uniquely determine MR_n and Mr_n, . Thus the samples and 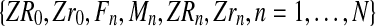contain the same information.

The following summarizes our proposed EM algorithm to estimate the parameters of the model:

• Step 0. i = 0. Set each component of (p^R(0),p^r(0),α⁽⁰⁾) to some strictly positive values.

• Step 1 (E Step). Based on (p^R(i),p^r(i),α⁽ⁱ⁾),

  • (a) determine and

  • (b) calculate .

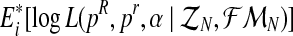• Step 2 (M Step). Obtain the vector

  

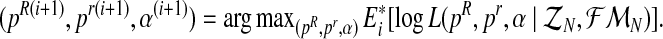
• Step 3. If 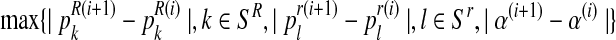is less than some convergence criterion, stop and denote by (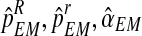) these final estimates. Otherwise, increment i by 1 and repeat steps 1–3.

Finally, we would point out that since m_R and m_r are obtained from p^R and p^r, respectively, then, from and 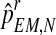, one can obtain the expectation-maximization MLEs for m_R and m_r based on 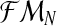, which will be denoted by 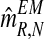and 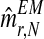, respectively. Also, one can obtain a sample of the distribution of (F_N+s, MR_N+s, Mr_N+s) knowing 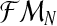for any s > 0 by simulating, through the Monte-Carlo method, s generations of a Y-linked BBP with preference starting with (ZR_N, Zr_N) and considering 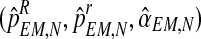as the parameters of the model. This allows one to forecast the number of individuals and couples for unobserved generations.

4. Simulation study

The method presented in the previous section will now be applied using the R statistical computing language and environment (R Development Core Team, 2012) to estimate the parameters of a Y-linked BBP with preference using simulated data. To this end, we consider a process with the following parameters: the probability to be female is α = 0.4 and the reproduction laws of each type of couple are 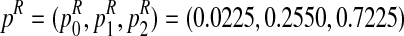and .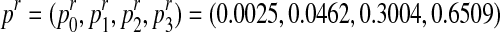

Note that we have chosen the sex-ratio to be less than a half since, in most populations, the sex-ratio is different from 0.5, and the analysis of Y-linked gene evolution turns out to be more interesting when α < 0.5 (González et al., 2006 and González et al., 2008). Also, the average number of individuals generated by each type of couple are m_R = 1.7 and m_r = 2.6, respectively, reflecting the possible difference between the reproductive capacity of mating units of each type that exists in nature.

For this model, we simulated 20 generations starting with (ZR₀, Zr₀) = (3,10). Table 1 lists the sample fm₂₀ formed by the total numbers of females and of males of each type obtained in these generations. The relatively small amount of sample information that this represents would make it difficult to determine at first sight anything about the future behavior of the Y-linked character on the basis of these observations.

Table 1.

Simulated Data

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Fn	15	18	20	21	21	22	24	29	24	20	23	21	16	15	18	19	16	15	15	15
MRn	4	2	2	4	3	4	4	4	3	5	7	7	7	4	3	5	3	4	3	4
Mrn	16	16	25	27	26	25	29	27	44	34	18	27	25	15	14	16	24	16	19	17

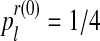Let us now apply the EM algorithm using the above sample, fm₂₀. To start the algorithm, we need the initial values (p^R(0), p^r(0), α⁽⁰⁾). Assuming the lack of information, we choose the values p^R(0) and p^r(0) according to uniform distributions of sizes 3 and 4, respectively. Thus, , with k = 0, 1, 2 and , with l = 0, 1, 2, 3. The best option to initialize α⁽⁰⁾ is the MLE of α based on the entire family tree, 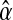(see Eq. (5)—recall that 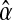only depends on the values recorded in fm₂₀). Therefore, as was indicated in the previous section, the sequence 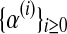is constant, and of value 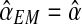— in the example, equal to 0.416.

We ran the EM algorithm and observed the sequence 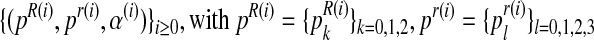and 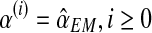, to converge from iteration 500 onwards (with the difference between consecutive elements of the sequence being less than 10⁻⁵). The values obtained in the last iteration were taken to be the expectation-maximization ML estimates. A discrete sensitivity analysis applied to study the influence of the initial values (p^R(0), p^r(0), α⁽⁰⁾) on the convergence of the method showed that the procedure is stable with respect to the initial values, with there being no changes in the limit.

From 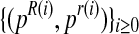, it is straightforward to obtain the sequence 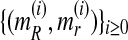with the means of the distributions p^R(i) and p^r(i), respectively, in each iteration of the method. This last sequence converges to the expectation-maximization MLEs for m_R and m_r, denoted by 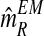and 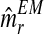, respectively. 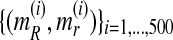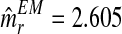From the values of the sequence , one obtains that they are quite stable from iteration 200 onwards, with the resulting expectation-maximization ML estimates of m_R and m_r based on fm₂₀ being and , respectively.

In order to analyze the consistency of the expectation-maximization MLEs, we next applied the EM algorithm by varying the number of generations observed, that is, we applied the algorithm 20 times, taking the sample to be fm_N, with 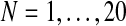. Each of these times, we performed 500 iterations of the method and saved the estimates given in the last iteration, taking them to be the expectation-maximization ML estimates of the corresponding parameters. At the end of the process, we thus had a sequence with 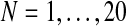. The three components of this sequence are plotted in Supplementary Figure S1. The more generations one has, the closer the estimate approaches the true value of the parameter (dashed line). Actually, under weak general conditions, the EM method leads to consistent estimates (McLachlan and Krishnan, 2008), as in the case of the usual MLEs based on complete data samples (see Supplementary Material).

To approximate the sampling distributions of 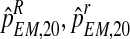, and 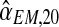, we applied a bootstrap procedure, making use of the EM estimates obtained on the sample fm₂₀ (i.e., the values of 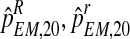, and 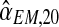. These values were used as parameters to perform a Monte-Carlo simulation of 2,000 processes until generation 20. For each of these bootstrap samples, we applied the EM method thus obtaining bootstrap approximations to the sampling distributions of 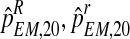, and 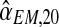. Obviously, from them it is straightforward to obtain a bootstrap sample of and 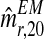. Supplementary Figure S2 illustrates the bootstrap approximation to these sampling distributions. One observes that the variability associated with the distribution of was greater than that of 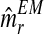. This may have been because there were fewer R males recorded in each generation than r males.

An interesting question applied is to predict, on the basis of the observed data, whether or not the process will survive over time. Theoretically, it is known that the condition α < 0.5 and 1 < (1 − α)m_R < αm_r ensures that there exists a positive probability for both genotypes to grow without limit over time (González et al., 2008). From the bootstrap approximation to the sampling distributions of 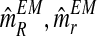, and 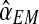, we calculated the proportion of samples in generation 20 that satisfie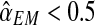d and 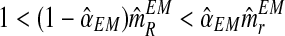, finding the approximate value 0.886. The high value of this calculated proportion is indicative that the theoretical condition might be satisfied. Indeed, the true values of the parameters do satisfy this condition, and therefore there exists a positive probability that both genotypes grow over the course of the generations.

Finally Supplementary Figure S3 illustrates the predictive distribution of the total numbers of females and of each type of male in the 21st generation. The predicted behavior is in keeping with the fact that there exists a positive probability that both genotypes survive over time.

5. Concluding remarks

In order to study the natural selection of Y-linked genes, the estimation of the main parameters of the Y-linked BBP with preference has been considered in a general nonparametric context. The model assumes males can be distinguished by certain genetic characteristics linked to the Y chromosome, characteristics which they either do or do not possess. The females choose their mates preferentially according to whether or not this characteristic is present. Firstly, we assumed that the entire family tree can be observed up to some generation and obtained the corresponding MLEs, studying their asymptotic properties—consistency and limiting normality. The procedure applied represented a methodological adaptation to the Y-linked models of some classical estimation theory procedures used in branching processes. Secondly, we considered the problem of estimating the main parameters of the model using only the sample information that is usually more plausibly observable in practice—that given simply by the number of females and of the two different types of male in each generation. We approached this problem as an incomplete data estimation problem, applying the expectation-maximization method that has proven very effective in solving it. How well this estimation procedure works was illustrated by means of a simulated example, in which we also showed the consistency of the estimates, obtained bootstrap approximations to their sampling distributions, and inferred the behavior of the process for future generations. This second procedure represents the principal objective of the present communication, allowing the use of these Y-linked models in applied problems under realistic assumptions.

We also showed that, when the only observable data are the total number of mating units of each genotype, the expectation-maximization method cannot be relied on to operate appropriately in estimating the probability of an individual being female, the reason being that the incomplete data likelihood function may not be unimodal. We concluded that it is necessary to observe, as a minimum, the numbers of females and of both male genotypes in each generation to guarantee the validity of the method.

A line for future research is the question of inferences for the two-sex branching model introduced in González et al. (2009b), in which it is considered that Y-linked genes are not expressed in the phenotype of males, so that females mate following a blind choice. In this framework, the total number of mating units of each type is not determined one-to-one from the total number of females and males of each type, and a random component underlies the mating process. Computationally, therefore, sampling the branching tree latent vector, 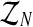, is more difficult and needs to be studied in some specific way. This complexity will probably lead to estimators whose sampling distributions will have large variances.

Acknowledgments

Research supported by the Ministerio de Economía y Competitividad and the FEDER through the Plan Nacional de Investigación Científica, Desarrollo e Innovación Tecnológica, grant MTM2009-13248.

Disclosure Statement

No competing financial interests exist.