Table 3.

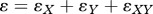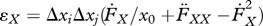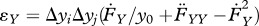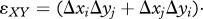
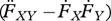The general expression of epistasis with and without pleiotropy. Equation (3.2) can be rewritten as (first row), where , and . If each of the alleles i and j acts on a distinct trait with no pleiotropic effect (figure 1b; Δx_j = Δy_i = 0, or, equivalently, Δx_i = Δy_j = 0), then one obtains ɛ_X = ɛ_Y = 0, and hence ɛ = ɛ_XY . However, for any decomposable function F(X,Y) = G(X) · H(Y) (second row), ɛ_XY = 0 because 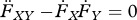. Therefore, when F(X,Y) = G(X) · H(Y), epistasis is non-zero only in the presence of pleiotropy, i.e. if ɛ_X and/or ɛ_Y are different from zero. For the particular case F(X,Y) = XⁿY^m (third row), epistasis is always zero, no matter whether or not there is pleiotropy.

	pleiotropic case (figure 1a)	non-pleiotropic case (figure 1b)
general F(X,Y)	ɛ = ɛX + ɛY + ɛXY	ɛ = ɛXY
F(X,Y) = G(X)·H(Y)	ɛ = ɛX + ɛY	ɛ = 0
F(X,Y) = XnYm	ɛ = 0	ɛ = 0