Escape from Adaptive Conflict follows from weak functional trade-offs and mutational robustness

Abstract

A fundamental question in molecular evolution is how proteins can adapt to new functions while being conserved for an existing function at the same time. Several theoretical models have been put forward to explain this apparent paradox. The most popular models include neofunctionalization, subfunctionalization (SUBF) by degenerative mutations, and dosage models. All of these models focus on adaptation after gene duplication. A newly proposed model named “Escape from Adaptive Conflict” (EAC) includes adaptive processes before and after gene duplication that lead to multifunctional proteins, and divergence (SUBF). Support for the importance of multifunctionality for the evolution of new protein functions comes from two experimental observations. First, many enzymes have highly evolvable promiscuous side activities. Second, different structural states of the same protein can be associated with different functions. How these observations may be related to the EAC model, under which conditions EAC is possible, and how the different models relate to each other is still unclear. Here, we present a theoretical framework that uses biophysical principles to infer the roles of functional promiscuity, gene dosage, gene duplication, point mutations, and selection pressures in the evolution of proteins. We find that selection pressures can determine whether neofunctionalization or SUBF is the more likely evolutionary process. Multifunctional proteins, arising during EAC evolution, allow rapid adaptation independent of gene duplication. This becomes a crucial advantage when gene duplications are rare. Finally, we propose that an increase in mutational robustness, not necessarily functional optimization, can be the sole driving force behind SUBF.

A major apparent paradox in molecular evolution is the concomitant requirement of innovation and conservation. New proteins are thought to evolve from existing proteins by mutation. But how can new protein functions arise if the existing functions are still required? Theories that attempt to reconcile this dilemma have relied almost exclusively on gene duplication. The oldest model, neofunctionalization (NEOF) (1), states that after a gene duplicates, the two resulting copies are functionally redundant. This allows one copy to accumulate mutations leading to a new function, while the other copy remains conserved. An alternative duplication, degeneration, complementation” (DDC) (2) model requires the ancestral gene to possess several subfunctions that are eventually distributed among its duplicate descendants by neutral mutations. NEOF and DDC both assume that the duplication itself has essentially no intrinsic advantage; thus fixation of duplications is viewed as purely stochastic. However, an increased gene dosage (i.e., increased concentrations of a protein) after duplication can be beneficial in itself (3, 4). In any event, neither of these models explains how adaptation to new structures and functions can occur on short time scales, especially when the necessary gene duplication does not occur or is lost by chance.

To tackle this question, a recently proposed model termed “Escape from Adaptive Conflict” (EAC) (5, 6) focuses instead on adaptation before gene duplication. As for DDC, EAC invokes subfunctionalization (SUBF) (3, 4), i.e., functional divergence from a multifunctional ancestral gene after gene duplication. Thus far, support for EAC has mostly been based on several experimental cases (5, 6). In EAC, a single gene can become multifunctional (i.e., acquire promiscuous functions) but is then mired in an adaptive conflict because optimization of each individual function is constrained. The resolution of this conflict is supposed to come from gene duplication and SUBF. However, a formal description of EAC is lacking (4); and the conditions for multifunctionality to be beneficial before duplication are unclear. It would be desirable, therefore, to develop a theoretical framework that incorporates ideas from all the aforementioned models to address pertinent experiments.

We embarked on this endeavor by first recognizing that enzymatic promiscuity (7) and fluctuations between alternative structural states (8, 9) may be understood in terms of neutral networks (10, 11). Such a network is defined as a collection of genes, or protein sequences, that produce the same phenotype (e.g., enzyme function or tertiary structure) and are interconnected by single-point (nonsynonymous) mutations. It is clear from observations of mutational robustness in proteins that neutral networks exist (12–18), although the topologies of real gene networks are largely unexplored due to the high dimensionality of sequence space. For this reason, theoretical investigations of neutral networks usually employ simple biophysical models of proteins (16, 19–27).

High network connectivity has long been predicted (28) and experimentally verified (17) to be correlated with high thermodynamic stability, leading to a funnel-like stability distribution in protein sequence space. Simulations (24) indicated that these superfunnels (28) can act as attractors on evolving protein sequences, often with one maximally connected, “prototype” sequence (gene) at the center that exhibits the highest native state stability (27, 28). Inasmuch as the selection of nonnative functions and structures (29–31) is operative, the attraction of any superfunnel towards its prototype may extend to proteins that are not yet part of its neutral network (24). In this picture, sequences between two neutral networks can serve as “bridges” [or “switches” (27)] for transitions from one network to another by encoding proteins with bistable native structures (8, 32, 33). An example of such phenomena is provided by recent experiments on the mutational transition between two different structural domains of protein G (34). Similar features have also been observed for RNA (35). Building on these advances, here we present a theoretical framework that addresses properties of neutral networks, gene duplication, dosage effects, and promiscuity as well as selection pressures, and how these factors may contribute to resolving the innovation/conservation dilemma.

Results

A tractable, physical model of neutral network topologies is required for the elucidation of SUBF in the evolution of multifunctional proteins. For this purpose, we adopted a simple two-dimensional hydrophobic-polar 18-mer protein chain model that provides a complete sequence-to-structure mapping (21, 24, 26–28). This protein model is based upon the biophysical hydrophobic-polar (HP) effects in folding and provides the thermodynamic stabilities for all conformations for a given sequence. It identifies in particular the most favorable (native) structures and allows for the possibility of multiple (degenerate) native structures that we take as a proxy for multifunctionality, i.e., by associating each alternative native structure with a different biological function. Fitness in the model is based on the stabilities of the functional structures. We consider a protein that was initially optimized for a single function, but a subsequent change in environmental conditions led to the addition of a second selection pressure that favors a different function. Evolutionary dynamics was modeled by a master equation for infinite populations and by Monte Carlo (MC) simulations for finite populations (see Methods and SI Text).

Relative Stabilities of Structural States Determine Multifunctionality.

Here we define a genotype as either a single gene or a pair of genes that originates from gene duplication. A gene pair is inherited as a single unit. A “gene” in our model corresponds to a protein sequence. As a chain molecule, a protein can fluctuate between different conformations or structural states. Globular proteins often have essentially only one maximally stable (ground-state) native structure under physiological conditions; but the probability for any other (“excited-state”) conformation is nonzero. Thus, apart from the function performed by the native conformation(s), excited-state conformations can perform promiscuous functions. In our model, the fitness of a genotype with respect to a conformation X_l (with a beneficial function) depends on a functional concentration C_l. For a single gene, C_l is equal to the fraction Φ(X_l) of protein molecules with the given sequence that adopt X_l. For a gene pair, C_l is equal to either the sum of Φ(X_l)’s of the two sequences or the larger of the two Φ(X_l) values, depending on the assumption about dosage effect (see below). The total fitness of a genotype is the sum of contributions from two different X_l’s (see SI Text, Eqs. S2 and S3).

Near-Neutral Network Topologies From a Biophysical Model.

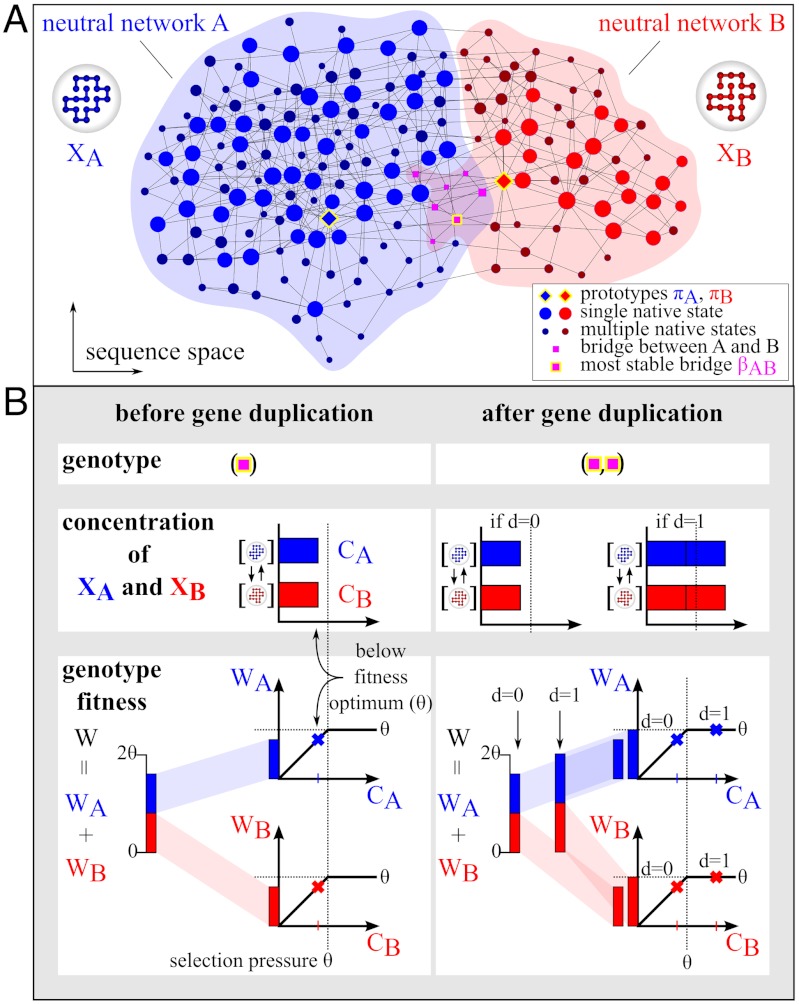
We considered two interconnected model neutral networks, A and B, that encompass a total of 185 gene sequences (Fig. 1A). Each network has one prototype gene (specialist (7), π_A and π_B) with maximum native stability, i.e., maximum fractional population for the native structure. Mutations among sequences in a neutral network preserve the native-state structure in our model; but they can alter native stability (28) (see Methods and SI Text). Hence, strictly speaking, some of these mutations are nearly but not exactly neutral (36, 37). We nonetheless refer to these networks as “neutral”. Of central importance to EAC are multifunctional (or generalist) “bridge” genes that include both target structures in their native states. Among the bridge genes, β_AB is the one that has the highest native stability (i.e., with identical largest fractional populations Φ(X_A) = Φ(X_B) for X_A and X_B).

Fig. 1.

A biophysical model of neutral network topology and fitness. (A) The extent of the inter-connected neutral networks A and B (for the depicted structures X_A and X_B) are indicated, respectively, by lightly colored regions of blue and pink. Their region of overlap is in light magenta. Symbols (nodes) represent model protein sequences (genes) with either X_A or X_B (diamonds for prototypes, circles otherwise), or both (magenta squares), in their native states. Sequences that differ by one point mutation are connected by edges. Symbols for sequences with single and multiple native conformations are shown, respectively, in lighter and darker colors. Nonprototype sequences encoding for more stable native states are denoted by larger symbols. (B) Fitness before and after duplication of a multifunctional gene (square). A genotype is either a single gene or a pair of genes that originates from duplication. Fitness of a genotype is the sum of fitness contributions W_A and W_B, which are functions of C_A and C_B respectively. As illustrated by the examples shown, W_A and W_B increase linearly, respectively, with C_A and C_B below a threshold concentration θ (dotted vertical line) and is a constant above θ.

Neutral or Advantageous Gene Duplications.

As described in Methods and SI Text, the fitness of a multifunctional gene in our model is based on the concentrations C_A and C_B, respectively, of the folded structures X_A and X_B, and total fitness of a genotype is the sum of the individual fitness contributions from X_A and X_B (Fig. 1B). The dosage parameter d characterizes two scenarios of how a gene duplication event affects fitness. The d = 1 scenario envisions protein concentrations are increased by gene duplication because it allows two independent loci to be expressed in parallel. Under such a positive dosage model (38, 39), gene duplication is beneficial, especially when suboptimal (promiscuous) functions are involved (40). As a control, we also studied a d = 0 scenario that envisions no dosage increase upon duplication in order to explore consequences of the assumption in standard NEOF and SUBF models that the gene duplication itself is neutral (3, 4). In contrast to the d = 1 model, the functional concentration of a beneficial structure in the d = 0 model is determined not only by the total population but also the thermodynamic stability of that structure (see SI Text). Most real situations probably lie in between the two extremes (41–43).

Fitness Trade-Offs Between Two Structural States.

Adaptive conflicts can arise between two or more structural states. Directed enzyme evolution experiments suggest that both weak and strong trade-offs exist and are underpinned by a variety of mechanisms (7). As an upper bound on fitness, θ serves to parametrize selection pressure because mutations are neutral if the protein concentrations both before and after the mutation are above θ (Fig. 1B and Fig. S1). A strong selection pressure tends to result in a strong trade-off because it penalizes any mutation that decreases the concentration of the existing native structure in favor of a different structure, i.e., a specialist is more favored than a generalist. A weak selection pressure tends to result in a weak trade-off because destabilizing mutations are allowed as long as a certain minimum concentration is maintained. These trends are illustrated in Fig. 2 by two representative θ values that we used in our simulations. As stated above, we made a simplifying yet instructive assumption that the combined fitness of two different structures is the sum of two individual fitness values. Combined fitness can take other forms. For example, the product of fitness contributions may be used when X_A and X_B form a protein complex [as for the Rop dimer (44)], in which case losing only one structure would prevent the entire dimer from forming and hence reduce fitness to zero. Consideration of such alternate fitness functions, however, are beyond the scope of the present work.

Fig. 2.

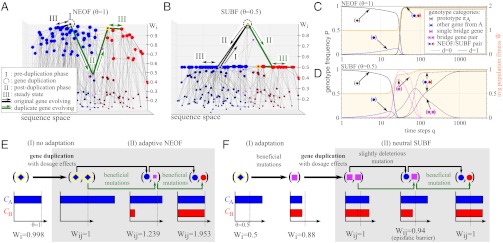
NEOF and SUBF occur under different degrees of fitness trade-offs. (A, B) Examples of fitness landscapes are shown for the network in Fig. 1A under high (A) and low (B) selection pressures. Single-gene fitness W_i is plotted along a vertical axis orthogonal to a planar representation of sequence space used in Fig. 1A. Note that gene-pair fitness W_ij = W_i + W_j is not plotted in these landscapes. A key to the symbols used to describe major evolutionary processes on these landscapes are provided in the Insets in A and in C . C, D Evolutionary dynamics simulated using the master equation formulation in SI Text for the fitness landscapes in A and B, respectively. Genotype frequency P (left vertical scale) provides the relative population of the sum of P_i(q)’s (for single genes) or of P_ij(q)’s (for gene pairs) that belong to a given genotype category as a function of time (q, in logarithmic scale). The corresponding evolution of average population fitness 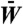is plotted in orange (right vertical scale). Evolution in the two scenarios of dosage effect after gene duplication (d = 0 or 1) are also compared. (E, F) Schematics of evolutionary steps during NEOF (E) and SUBF (F) with dosage effects (d = 1). Genotype fitness is given as W_i (single genes) or W_ij (gene pairs) that depends on protein concentrations C_A and C_B (cf. Fig. 1B).

Simulations of Evolution Under Two Selection Pressures.

The fitness landscapes (45) in Fig. 2 A and B provide the variation of single-gene fitness W_i in evolutionary dynamics started with only gene π_A in the population at time q = 0, assuming that only X_A was selected for previously; but with the commencement of the simulation a second equally strong selection pressure for X_B became operative. Hereafter, a constant point mutation rate allows other single genes to be populated over time. A gene duplication rate also permits pairs of genes to be created. The gene pairs first carry identical copies of the same gene, but the individual genes in the pair can then further evolve by point mutations (SI Text, Eqs. S4 and S5). The time evolution of the relative population, P(q), of various genotypes and the average population fitness 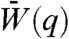are tracked in Fig. 2 C and D. All results in the main text were obtained using the master-equation approach. MC simulation results are reported in SI Text for comparison.

NEOF is the Result of Strong Selection Pressures.

The fitness landscape in Fig. 2A (also see Movie S1) is dominated by two peaks at the prototypes π_A and π_B (yellow-rimmed blue diamonds). The resulting simulated evolutionary dynamics exhibits the classical NEOF pattern (Fig. 2C). Owing to the high selection pressure and the resulting strong fitness trade-off, mutations in π_A are always deleterious; hence there is no adaptation before duplication (phase I in Fig. 2A), even though there is limited redistribution of population from the prototype π_A to other single genes encoding for X_A (see variation for q < 20 in Fig. 2C). After a duplication of π_A (dashed circle), the second gene copy can then adapt towards the new function (green line; phase II) via evolutionary paths that may traverse intermediate genotypes of low fitness (such as the bridge lying along the green path in Fig. 2A) yet still maintain a monotonic increase in fitness (Fig. 2E). Finally, at steady state (phase III), only NEOF gene pairs with one gene from each network becomes significantly populated. Irrespective of dosage effect (d = 0 or 1) at duplication, these gene pairs rise to fixation rapidly with an almost simultaneous increase in fitness.

SUBF is the Result of Intermediate Selection Pressures.

In contrast to Fig. 2A, the fitness landscape in Fig. 2B (also see Movie S2) representing a weak fitness trade-off is mostly flat because many mutations leave fitness essentially unchanged. Now SUBF is observed instead of NEOF. This is the result of lowering θ from 1.0 to 0.5. Because half of the maximum protein concentration is sufficient for optimal function, the sum of fitness contributions from both target structures encoded by the bridge genes allow one of these genes (β_AB, yellow-rimmed magenta squares) to form a single fitness peak in between the two neutral networks for X_A and X_B, enabling adaptation before duplication (phase I) and leading to a high transient population of bridge genes (magenta peak in Fig. 2D) accompanied by a strong increase in fitness. If dosage does not increase (d = 0), gene duplication does not provide any immediate advantage. As a result, single bridge genes (I) rise to higher frequencies and, because thermodynamic stability is preferred (see SI Text), subfunctionalize very rapidly (II + III in Fig. 2B) after duplication (dotted curves in Fig. 2D). Genotypes with pairs of bridge genes have only negligible frequency during this process. If dosage increases (d = 1), the duplication of bridge genes provides a further fitness increase. In this case, SUBF (II) does occur eventually (III); but it is a slow, essentially nonadaptive process (solid curves in Fig. 2D) because the population as a whole is already very close to the fitness optimum during an intermediate evolutionary stage with a significant transient bridge pair population long before SUBF was completed: In Fig. 2D, the transient bridge pair peaks at time q ≈ 80 and does not come close to zero until q ≈ 800, whereas the population average fitness 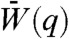at q = 200 is already within 0.21% of the optimal value of 0.994851. We will discuss this phenomenon in more detail below. The trend seen here appears to be quite general. Using the same parameters, NEOF and SUBF with features similar to those in Fig. 2 were consistently observed in MC simulations of small finite populations (SI Text) evolving on the same network (Fig. S2). The same pattern of behaviors was also observed in master-equation results for different networks (Table S1 and Fig. S3) and for different fitness parameters (Fig. S4). We also found that multifunctionality is particularly advantageous when gene duplications are rare (Fig. S5).

SUBF as a Consequence of Neutral Network Topology.

Fig. 2F provides a schematic overview of the SUBF process with dosage effect (d = 1) in Fig. 2D. To delineate the role of neutral events in SUBF after gene duplication, Figs. 2F and 3 focus on gene pairs with maximum fitness. Among them, the 24 bridge pairs are vastly outnumbered by the 1,728 subfunctionalized pairs. One expects, therefore, that SUBF is driven at least partly by a “genotype-space entropy.” In analogy to equilibrium statistical mechanics, SUBF should be favored because it is the macrostate with more underlying microstates compared to other macrostates with equal fitness. However, insofar as evolutionary kinetics is concerned, there is an epistatic (45) “barrier” that hinders mutational exchange between bridge pairs and subfunctionalized pairs (Fig. 2F) in our model: The first mutation towards SUBF converts a bridge gene into a gene from either A or B, making a “mixed pair” (one bridge, one g = 1 nonbridge). This is slightly deleterious because either C_A or C_B is reduced to the level before gene duplication. The balance between C_A and C_B is restored only by a second complementary mutation in the remaining bridge gene. This epistatic barrier also diminishes the rate of back-mutations towards bridge pairs, like a ratchet, and subfunctionalized genotypes prevail once this barrier is overcome.

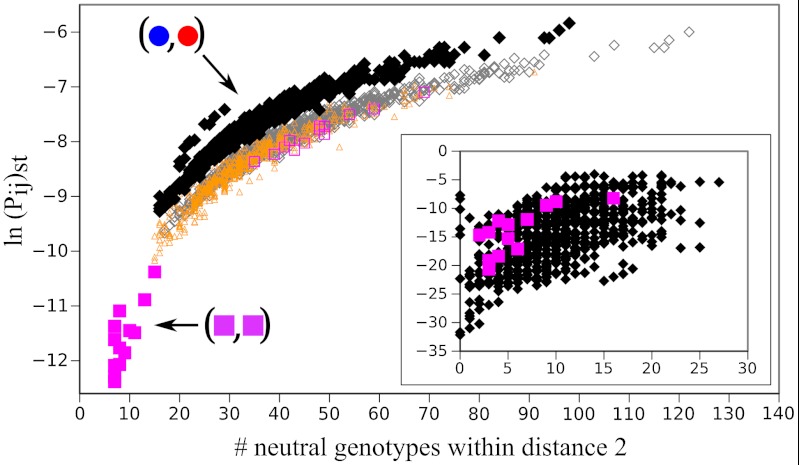
Fig. 3.

Strong tendency towards mutationally robust genotypes during SUBF. Steady-state populations 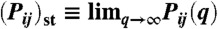were obtained from the SUBF simulations in Fig. 2D (θ = 0.5 and d = 1). The scatter plot shows ln(P_ij)_st versus the number of genotypes that are within two point mutations from (i,j) in the network. Data points for the 24 bridge pairs and 1,728 subfunctionalized pairs are plotted, respectively, by filled magenta squares and black diamonds. The plot thus contains all 1,752 genotypes with maximum fitness at steady state (among all 34,410 genotypes—single genes and gene pairs—for X_A and X_B in Fig. 1A). The corresponding scatter plot for a randomized network topology is shown in the Inset. Results from a control simulation that artificially eliminated the epistatic barriers are shown by the open symbols. Magenta squares, orange triangles, and gray diamonds represent data points for bridge, mixed, and SUBF pairs, respectively. The inclusion of mixed pairs with ad hoc optimal fitness leads to increased numbers of neutral genotypes adjacent to the bridge pairs and thus abolishes the separation between bridge and SUBF pairs observed in the original model. Nevertheless, a tight correlation between ln(P_ij)_st and genotype entropy is maintained and SUBF pairs remain the most populated steady-state genotypes.

We further assessed the role of network topology on SUBF by applying our evolutionary master-equation dynamics. The steady-state populations of the aforementioned gene pairs with maximum fitness are shown in Fig. 3 (filled magenta and black symbols). For clarity, less fit, and thus less frequent, genotypes are not plotted. Previous studies showed that single genes that have more adjacent genes, i.e., enjoy more mutational robustness, have higher steady-state populations (28, 46). Fig. 3 shows that a similar effect applies to gene pairs: The logarithm of steady-state frequency of a gene pair, ln(P_ij)_st, is positively correlated with the number of other gene pairs with the same fitness within two point mutations of the given pair. A clear separation exists between the low-robustness bridge pairs and SUBF pairs, with the right-most data points in Fig. 3 corresponding to SUBF pairs with two prototype genes that have many neutral neighbors. A similar though less prominent trend is also apparent in the scatter plot of ln(P_ij)_st versus the number of gene pairs separated from (i,j) by one point mutation (Fig. S6). The general pattern in Fig. 3 was observed in other model networks as well (Fig. S6). As a control, we imposed a random topology on the gene pairs studied in Fig. 3 (in which case the network topology would no longer be a consequence of the physical protein chain model; see SI Text) and computed the resulting ln(P_ij)_st values. The resulting scatter plot (Fig. 3, Inset) shows no clear separation between bridge and SUBF pairs; thus demonstrating that the trend seen in the corresponding scatter plot in Fig. 3 (filled symbols) is a consequence of a particular class of network topologies. Taken together, these results show clearly that evolution in neutral networks based on biophysics of protein folding tends to favor mutationally robust SUBF pairs in the steady state.

For the system in Fig. 2D, the average fitness of SUBF, bridge, and mixed pairs is 0.99, 0.86, and 0.75, respectively, whereas the rest of the 34,225 gene pairs in the model have significantly lower fitness. Our evolutionary dynamics initiated with the entire population set to the most stable bridge pair with optimum fitness still led to SUBF. Thus, as exemplified by this case, SUBF can be nonadaptive. Our simulation showed further that the very gradual increase in 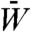to attain the last ≲0.21% of optimum fitness for the d = 1 case in Fig. 2D is mainly caused by a transfer from the small population of mixed-pair epistatic barriers to SUBF pairs.

Although the evolution from bridge pairs to SUBF pairs involves surmounting an epistatic barrier in our model, the existence of such a barrier is not necessary for the prevalence of SUBF pairs in the steady state. As a control, we performed a simulation in which epistatic barriers were artificially eliminated by resetting the fitness of mixed pairs from a suboptimal value to the maximum value of 2θ equal to that of the (β_AB,β_AB) pair and the SUBF pair (π_A,π_B). The resulting scatter plot is shown by the open symbols in Fig. 3. Even under this ad hoc condition, SUBF pairs (gray diamonds) with higher degrees of mutational robustness remain the most populated genotype in the steady state. Generally speaking, an epistatic barrier is likely when the single bridge gene has low stability relative to both the selection pressure and the average stability of stable nonbridge proteins. It would be interesting to investigate whether epistatic barriers similar to those in our model are common in natural protein evolution. Conceivably, mutations in natural proteins may allow for small changes in the concentration ratio of the two target structures instead of the large changes in our model. In that case epistatic barriers would be less significant. This remains to be ascertained.

Discussion

Fast Protein Evolution Under Dual Selection Pressures.

NEOF, SUBF, and dosage effect now can all be seen as parts of one unifying theoretical framework. Consistent trends were observed in our master-equation approach for an effectively infinite population and in our MC simulations for a large yet finite population of 1,000 individuals. As stated above, our effort was motivated by recent experimental findings that enzymes can be promiscuous (7, 47, 48) and that proteins can fluctuate between different structures with different biological functions (8, 9, 33, 49). Recent computational studies have demonstrated that selection on excited states can indeed speed up evolution to a single nonnative structure (24), and that evolvability is positively correlated with structural/phenotypic fluctuation (26). Here we showed further that such a general mechanism also enables adaptation driven by two selection pressures either before (SUBF) or after (NEOF) gene duplication. It has been argued that early “proto-enzymes” were more likely to be promiscuous (7, 50–52), and that these primordial enzymes subsequently duplicated and diverged to form more specialized descendants. Our analysis here suggests that this divergence was driven not only by positive selection but also by the mutational robustness in near-neutral networks.

EAC, DDC, and Dosage Effect.

The adaptation period before gene duplication in our model is most compliant with EAC; but neutral SUBF (a feature of DDC) is possible in the presence of dosage effect (Fig. 2D), while adaptive SUBF (a feature of EAC) is observed in the absence of dosage effects and a preference for thermodynamic stability. Nonetheless, the observed increase in mutational robustness (neutral SUBF) could also be interpreted as a type of slow adaptation, because high robustness eventually leads to more viable offspring. This would comply with EAC. DDC may generally be more apt to describe the divergence of regulatory subfunctions, as originally intended (2). Recent model classifications (3, 4) stated that the fixation of gene duplication is neutral in both DDC and EAC. In contrast, our model shows that if duplications of multifunctional proteins are associated with a positive dosage effect, the duplication step can be advantageous in itself, and this very step alone may even be sufficient to achieve optimal fitness (Fig. 2 D and F and Fig. S4A).

EAC in the Real World.

A few case studies are indicative of EAC of multifunctional ancestral proteins (6, 53, 54). EAC is characterized by conflicting pressures to conserve and adapt before gene duplication. During this EAC stage, one expects the ratios of nonsynonymous and synonymous substitution rates, K_a/K_s, to be either > 1 because of adaptive evolution (6) or ≈1 because of a cancellation of effects from positive and purifying selection. After gene duplication, the SUBF process in EAC is constrained to a neutral network with weak purifying selection (3, 4, 38), thus K_a/K_s < 1 is expected. Based on experiments showing that a reconstructed common ancestor of the fluorescent proteins in corals that emit either red or green light can emit light of both colors (53), a K_a/K_s analysis of the rounds of duplication and divergence in the evolution of coral pigments is suggestive of EAC (SI Text). Note that the K_a/K_s pattern of NEOF would differ from that of EAC because in NEOF one copy after duplication is conserved (K_a/K_s < 1), only the second copy evolves and is positively selected (K_a/K_s > 1).

Results here indicate that EAC requires a regime with relaxed purifying selection (intermediate θ values). Thus, in contrast to highly conserved proteins that probably have evolved by NEOF, EAC is most likely operative in protein families that are not essential for survival, but that can provide a significant selective advantage if properly adapted. EAC should be particularly useful for proteins that have to quickly adapt to an ever changing environment, which is especially true for sessile organisms such as plants (6, 54). EAC may also be advantageous in arms-race scenarios such as antibiotics resistance and host-parasite interactions.

EAC and Population Size.

Our prediction of robustness-driven EAC/SUBF is based on master-equation computation for infinite population (N → ∞, Figs. 2 and 3) and MC simulation for a population of 1,000 with μN = 36 (see SI Text, Figs. S2 and S5B). For N → ∞, steady-state population distribution depends only on sequence-space topology and is independent of mutation rate (28, 46); but the dependence of population on robustness can break down for μN ≲ 1 (46). Inasmuch as the validity of robustness-driven SUBF is governed by μN, the present results should be applicable at least to viruses (e.g., the tobacco mosaic virus has μN≫100 based on N ∼ 2 × 10⁷ and per-base-pair and genomic mutation rates of μ ∼ 10^-5 and ∼0.05, respectively) (55) and prokaryotes with μN ∼ 100 (based on data in ref. 56 and assuming approximately 1,000 nucleotides per gene), though μN’s for vertebrates are much lower (e.g., μN < 1 for humans) (56).

Importance of Neutral Network Topology.

A realistic account of neutral network topologies is of critical importance in evolutionary modeling. We use an explicit-chain model with physics-inspired interactions for this purpose. In this respect, our approach is distinct from and complementary to analytical methods that were based on random sequence-space topologies (57) or did not use an explicit chain model to ascribe mutational effects (58). We expect our general conclusions to be valid for any neutral network topology that emphasizes similar biophysical principles of hydrophobic-polar driving forces in protein folding, as there is experimental support for the validity of these principles in neutral networks of real proteins (14–16, 18, 59, 60).

Outlook.

Our model focuses primarily on protein stability, single duplications of complete genes, and cases with μN ≳ 40. Future work will need to address other factors such as gene expression (61), the interactions within gene regulatory (62) and metabolic networks (63), the possibility of multiple duplications of the same gene in rapid succession (40), and cases of smaller μN (46). Nonetheless, our quantitative framework has already revealed an intricate interplay among selection pressure, fitness trade-offs, dosage effect, and network topologies that can either promote or disfavor the NEOF or SUBF, DDC, or EAC scenarios.

In light of these findings, a more accurate and enriched picture awaits discovery through comparisons of protein stabilities and/or functions between lineages with or without gene duplication. Homologous threading and stability prediction methods can be applied to (paralogous) protein structures that receive mutations from different positions in a phylogeny. Under NEOF, the ancestral protein sequence should be stable for one of the paralogous structures, but not the other (given that the structures have sufficiently diverged). Under SUBF, the ancestor should be equally stable for both paralogous structures, but stability should be increased in both paralogs. This distinction should be useful in delineating the role of EAC in evolution.

Methods

Salient features of our model are outlined briefly below; technical details can be found in SI Text and a glossary of symbols is provided in Table S2. We consider chain sequences (genes) of 18 hydrophobic (H) or polar (P) monomers (residues) that configure on a two-dimensional square lattice. A conformation is a native-state structure of a sequence if it has the highest number of hydrophobic-hydrophobic (HH) intrachain contacts among all possible structures. The native state is the set of native structures; g is the total number of native structures for a given sequence. A native state is unique, or nondegenerate, if g = 1, otherwise it is degenerate (g > 1). The network in Fig. 1A consists of all g ≤ 6 sequences, each of which has either X_A or X_B, or both of these structures in its native state. Fitness was assigned according to the functional concentrations (fractional populations) of X_A and X_B as illustrated in Fig. 1B (see SI Text, Eqs. S1–S3).

Evolutionary dynamics was simulated primarily with an initial homogeneous populations (at q = 0) of a single π_A gene. Steady-state population distribution is independent of initial population but other initial populations were also examined for kinetic comparisons. Asexual, haploid reproduction without recombination was assumed. We used a deterministic master equation formulation (see SI Text, Eqs. S4 and S5) for an effectively infinite population, wherein the frequency, or population P(q), of each genotype at any given time step q was normalized to a fraction of unity. At each time step, a constant per-monomer mutation (H → P or P → H substitution) rate of μ = 0.001 was applied. This rate was used because it is sufficiently low to minimize multiple mutations per gene. The gene duplication rate is μ_d = 0.0001 per single gene. The resulting time-dependent genotype populations (P’s) and average population fitness 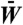were determined for all discrete time steps q = 0,1,2,… until a steady state was reached. A schematic overview of this approach is provided in Fig. S7. Analogous treatment of the evolution of finite populations of 1,000 individuals were conducted using MC simulation (see SI Text, Figs. S2 and S5B).