Price To Be Paid for Two-Metal Catalysis: Magnesium Ions That Accelerate Chemistry Unavoidably Limit Product Release from a Protein Kinase

Abstract

Incorporation of divalent metal ions into an active site is a fundamental catalytic tool used by diverse enzymes. Divalent cations are used by protein kinases to both stabilize ATP binding and accelerate chemistry. Kinetic analysis establishes that Cyclin-dependent kinase 2 (CDK2) requires simultaneous binding of two Mg²⁺ ions for catalysis of phosphoryl transfer. This tool, however, comes with a price: the rate-acceleration effects are opposed by an unavoidable rate-limiting consequence of the use of two Mg²⁺ ions by CDK2. The essential metal ions stabilize ADP product binding and limit the overall rate of the reaction. We demonstrate that product release is rate limiting for activated CDK2 and evaluate the effects of the two catalytically essential Mg²⁺ ions on the stability of the ADP product within the active site. We present two new crystal structures of CDK2 bound to ADP showing how the phosphate groups can be coordinated by either one or two Mg²⁺ ions, with the occupancy of one site in a weaker equilibrium. Molecular dynamics simulations indicate that ADP phosphate mobility is more restricted when ADP is coordinated by two Mg²⁺ ions compared to one. The structural similarity between the rigid ADP·2Mg product and the cooperatively assembled transition state provides a mechanistic rational for the rate-limiting ADP release that is observed. We demonstrate that although the simultaneous binding of two Mg²⁺ ions is essential for efficient phosphoryl transfer, the presence of both Mg²⁺ ions in the active site also cooperatively increases ADP affinity and opposes its release. Evolution of protein kinases must have involved careful tuning of the affinity for the second Mg²⁺ ion in order to balance the needs to stabilize the chemical transition state and allow timely product release. The link between Mg²⁺ site affinity and activity presents a chemical handle that may be used by regulatory factors as well as explain some mutational effects.

Introduction

Cyclin-dependent kinases (CDKs) are a family of Ser/Thr protein kinases that play a critical role in signaling progression through the eukaryotic cell cycle. Cyclin-dependent kinase 2 (CDK2)/Cyclin E heterodimers provide the phosphorylation signals that move the cell through the G1 to the S phase cell cycle restriction point, and CDK2/Cyclin A heterodimers then push it through the S phase.¹ To ensure proper cell cycle signaling, the specific catalytic activities of CDKs are regulated through a variety of mechanisms that either alter substrate recruitment and affinity or accelerate the rate of phosphoryl transfer. Monomeric CDK2 is essentially inactive, with both very low k_cat values and extremely high K_M values in vitro.² Crystal structures have shown how the allosteric activation of human CDK2 occurs by heterodimerization with a Cyclin protein binding partner and by phosphorylation of Thr160 on the kinase activation loop by an activating kinase.²⁻⁴ These both stabilize large-scale conformational changes that account for some, but not all, of the resulting gains in k_cat and substrate K_M values. A more complete description of the chemical mechanism of the fully activated enzyme is still needed if we are to understand how some mechanistically elusive regulatory factors effect CDK2 as well as explain how potentially oncogenic mutations can bypass normal regulation by either deconstructing or stabilizing essential features of the active enzyme.

The catalytic cycle of an active protein kinase is comprised of the binding of both ATP·Mg²⁺ and protein substrate, followed by the chemical step of phosphoryl transfer, and finally product release. Progression through all steps of the catalytic cycle is required to allow subsequent rounds of catalysis, and therefore, dynamic attenuation of the rate of any of the steps depicted in Figure 1A could provide a mechanism for regulation of kinase activity. Solvent viscosity effect studies of the fully activated states of many kinases, including CDK2, have shown that product release can be slow and often rate limiting.^5,6 At the same time, the somewhat similar magnitudes of the rates of the chemistry and product release steps in many protein kinases means that both steps can contribute to the overall reaction rate and the relative contributions may vary with conditions or activation state of the enzyme. One external factor that is known to affect CDK2 and most protein kinases in an often complex way is the concentration of divalent metals.^6,7

Figure 1.

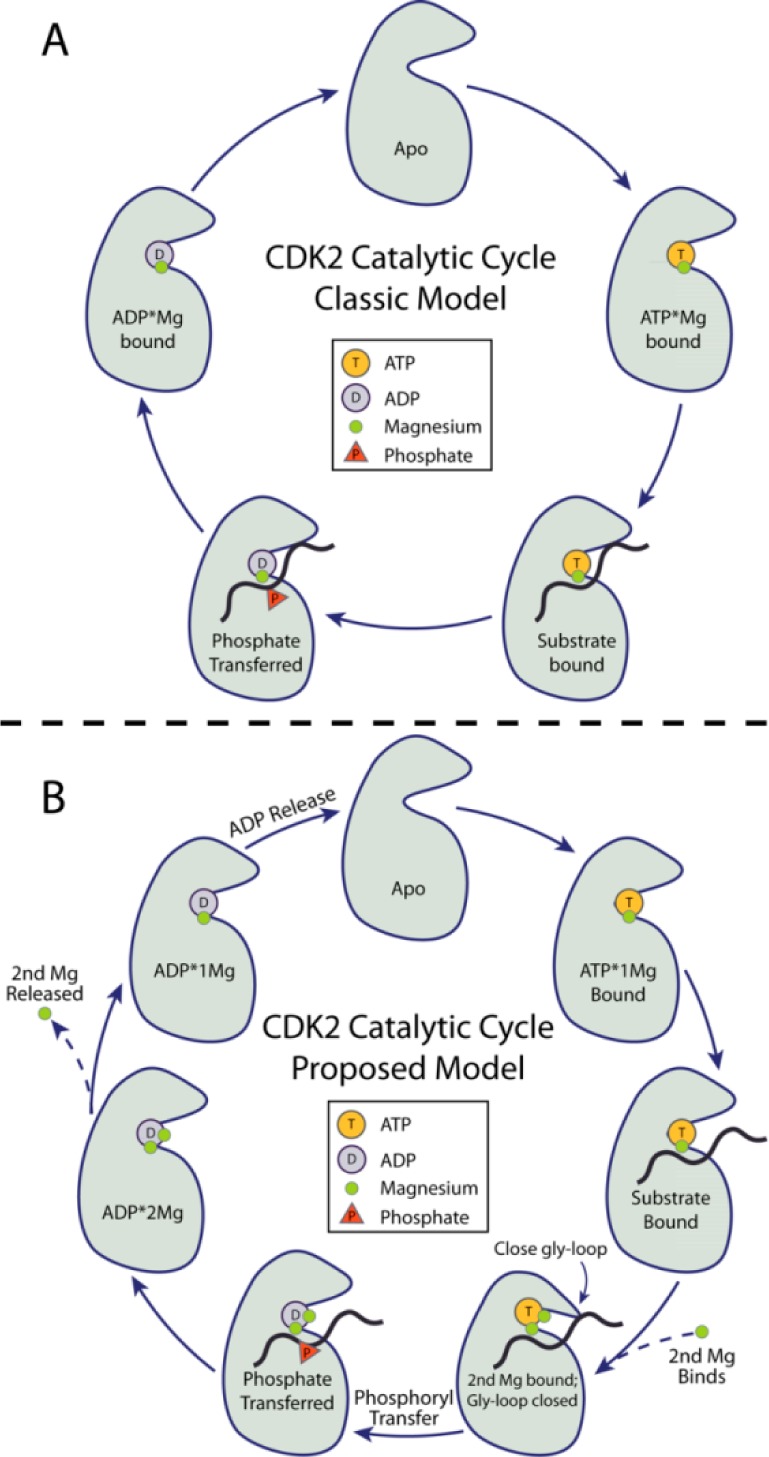
CDK2 catalytic cycle. (A) Classic model of protein kinase catalysis. (B) Proposed model where binding of a second Mg²⁺ ion prior to phosphoryl transfer and release of a second Mg²⁺ prior to ADP release are critical to efficient progression through the catalytic cycle.

The nucleotide binding and phosphoryl transfer steps of CDK2 are both strongly affected by the binding of divalent cations in the active site.^3,4,7,8 Mg²⁺ is by far the most abundant and available divalent metal ion in vivo, and it is believed to be the predominant protein kinase cofactor under physiological conditions.⁸ No ordered Mg²⁺ ions have been identified in CDK2 crystal structures in the absence of bound nucleotide, but ATP in the cell exists as a complex with Mg²⁺, and ATP·Mg is the substrate of most protein kinases.⁹ Although other divalent metal ions can sometimes be functional surrogates for Mg²⁺ in protein kinases in vitro,^10,11 we will focus specifically on Mg²⁺ because of its physiological relevance and because alternative divalent cations can function quite differently. Mg²⁺ ions are critical to the binding of anionic nucleotide phosphates because the active site region that surrounds the ATP phosphates is also strongly electronegative. Mg²⁺ ions neutralize the electrostatic replulsion by forming bridging contacts between the phosphates and electronegative protein functional groups such as Asp145 in the conserved kinase “DFG” motif. There are additional Mg²⁺ effects that are not fully understood. Some kinases have been described as possessing both essential and inhibitory divalent binding sites,¹¹ while other kinases are thought to catalyze phosphoryl transfer with a single or even zero divalent ions.¹² Given the strong effect that Mg²⁺ ions have on the activity of CDK2,⁷ it is essential to have a detailed understanding of the roles that Mg²⁺ ions play at each step of the catalytic cycle before we can truly understand how the enzyme functions and how it can be regulated.

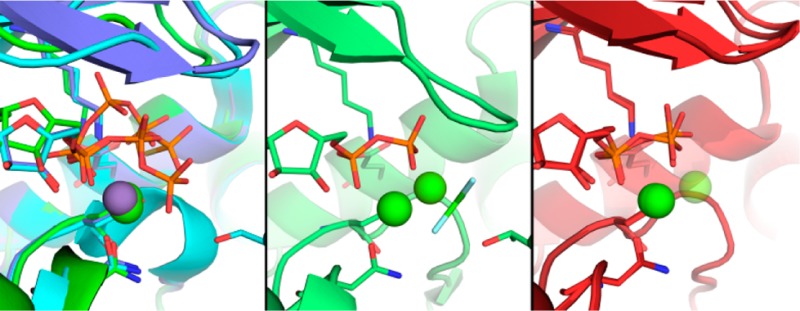
Structures of CDK2 bound to ATP or ATP analogues revealed at most a single divalent ion in the active site, as shown in Figure 2C. This metal, which is generally bound at a site that is structurally homologous to the site labeled MgII in two-metal/ATP structures of protein kinase A (PKA), coordinates the α- and β-phosphates to active site residues D145 (“DFG”) and N132. The structures we recently reported of a transition state (TS) mimic of the phosphorylated CDK2·Cyclin complex (pCDK2·Cyclin), crystallized in the presence of Mg²⁺, were the first to observe a second divalent simultaneously bound in the pCDK2·Cyclin active site.⁷ The second Mg²⁺ ion is bound at the site labeled MgI in Figure 2D, a site that is structurally homologous to the second divalent site observed in PKA. Although this second Mg²⁺ ion may only bind transiently during the complete CDK2 catalytic cycle, it is essential that both Mg²⁺ ions be simultaneously bound to achieve optimal catalysis of the phosphoryl transfer step.

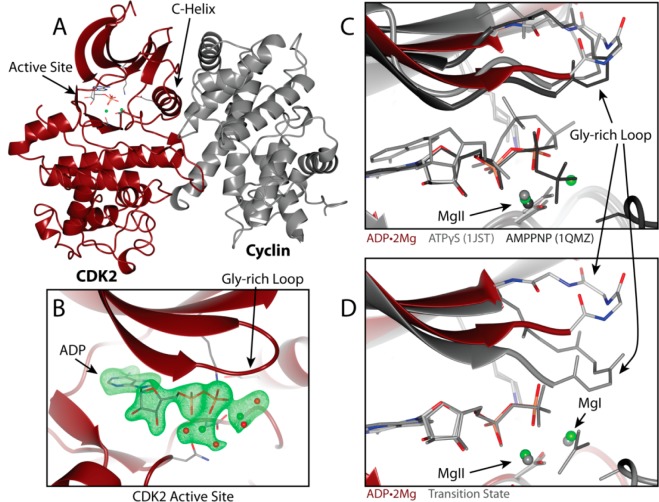
Figure 2.

(A) Overview of pCDK2·Cyclin A complex bound to ADP with two Mg²⁺ ions. pCDK2 is shown in maroon and Cyclin A in gray. ADP, D145, K33, and E51 are displayed in stick representation. Green spheres represent Mg²⁺ ions. (B) ADP·2Mg average kicked omit map. Green electron density is a positive mFo-DFc map contoured to 3σ; electron density clipped to within 2 Å of ADP, Mg²⁺, and coordinating water oxygen atoms. (C) Two Mg²⁺ ions are identified in the ADP·2Mg structure (maroon) but not ATPγS-bound pCDK2 (gray, 1JST)³ or AMPPNP-bound pCDK2 (black, 1QMZ).¹⁶ (D) Two Mg²⁺ ions stabilize the closed Gly-loop conformation in the transition state structure (3QHR)⁷ but not in the ADP·2Mg structure.

The active site of the two Mg²⁺-bound TS of pCDK2·Cyclin is conformationally distinct from the ATP·1Mg-bound structures. The conformation of the glycine-rich loop (Gly loop) in the TS is closed such that it makes additional electrostatic interactions with the phosphates and excludes water from the active site. Molecular dynamics (MD) simulation of either pCDK2·Cyclin bound to ATP or the TS mimic demonstrated that the binding of the second Mg²⁺ ion strongly stabilizes the closed conformation of the Gly loop and also notably reduces the conformational flexibility of the ATP phosphates. Furthermore, it was found that pCDK2·Cyclin activity increased dramatically (from 0 to 15 s^–1) as total Mg²⁺ concentration is increased over the range of 0–7 mM.⁷ All these data led us to propose a model for how the second Mg²⁺ ion functions as an essential activator of the chemical step by binding to the pCDK2·Cyclin·ATP·Mg·substrate complex, closing the Glycine-rich loop and stabilizing the TS to accelerate phosphoryl transfer.⁷ If the presence of both Mg²⁺ ions is essential for the phosphoryl transfer step, we can assume that both Mg²⁺ ions must be present in the active site immediately following bond cleavage, presumably coordinating the ADP^3– and the phosphorylated protein product in a way not unlike the geometry observed in the TS mimic structure.

In this paper we focus on the effects of the Mg²⁺ ions just after phosphoryl transfer when the reaction products are still bound within the active site and draw comparisons to the effects of the Mg²⁺ ions on stabilizing the TS for phosphoryl transfer. We use crystallography, molecular dynamics simulations, and enzyme kinetics to characterize the structural and energetic effects of the equilibrium binding of the two Mg²⁺ ions to the active CDK2·CyclinA enzyme. Taken together, our results suggest that binding of the second catalytically essential Mg²⁺ ion cooperatively stabilizes nucleotide binding to the extent that product release becomes rate limiting in the fully activated state of the enzyme. Structural and molecular dynamics data suggest that one of the two Mg²⁺ ions reversibly binds and that its release is coupled to conformational changes that facilitate release of the ADP·Mg²⁺ product. This more complex model for the multiple roles of the Mg²⁺ ions provides an explanation for why some kinases have been observed to be stimulated by Mg^2+13,14 while others are seen to be inhibited.¹⁵

We conclude that the two Mg²⁺ ions in the catalytic mechanism pose a conundrum; although the two Mg²⁺ stabilization of the reaction TS is an efficient mechanism for catalyzing phosphoryl transfer, the two divalent metals unavoidably limit the rate of ADP release. For CDK2, the binding of a second active-site Mg²⁺ to the MgI binding site illustrates how Mg²⁺ can alternatively function as both an activator and an inhibitor at different steps of the catalytic cycle. MgI functions in the former role when it activates phosphoryl transfer from ATP and in the latter when it suppresses the rate of ADP release. The activating and inhibitory Mg²⁺ binding sites in CDK2 are thus exactly the same site, with the two roles differentiated only by whether the nucleotide is in the ATP or ADP state.

Experimental Methods

Crystallography

Thr160 monophosphorylated human CDK2 (pCDK2) and mouse Cyclin A were expressed and purified as described previously.⁷ Purified pCDK2·Cyclin A complex was concentrated to 13.7 mg/mL using centrifugal filtration tubes. 0.65 μL of purified protein solution was mixed with 1.11 (final 4 mg/mL protein), 0.99 (final 4.5 mg/mL protein), or 0.89 μL (final 5 mg/mL protein) of the crystal condition. The crystallization condition is 22% w/v poly(acrylic acid) sodium salt 5100, 20 mM MgCl₂, and 100 mM HEPES pH 7.5. Apo crystals were grown in 96-well sitting-drop vapor diffusion trays at 20 °C. Large plate-like crystals appeared after 3–6 days and were allowed to grow for 3 weeks. Crystals were harvested with a nylon loop and transferred to a new drop containing 4 μL of ligand soaking/cryoprotection solution. Crystals were soaked for 1 h in 30% v/v glycerol, 3.2 mM ADP, 10 mM MgCl₂, 25 or 50 mM HEPES pH 7.5, and 2% w/v PEG-3350 before mounting on nylon loops or mesh mounts and flash freezing in liquid nitrogen. Diffraction data were collected at the 21-ID-G and 21-ID-D LS-CAT beamlines at the Advanced Photon Source (APS), Argonne National Laboratories. 180° of data were collected at 100 K with λ = 0.97872 Å, with a 0.5° oscillation range per frame. Data integration and scaling were performed with Mosflm¹⁷ and CCP4 Scala¹⁸ using the default options.

Initial phases were determined by molecular replacement using Phaser,¹⁹ using a previously solved structure of CDK2·Cyclin A. We removed the Gly-rich loop (residues 10–18), a loop N-terminal to the C helix (residues 37–42), and the activation loop (residues 153–166) from the CDK2 search model in an effort to minimize model bias from the initial phases, because of the observed flexibility of these regions of CDK2. The CDK2 and Cyclin A models were searched separately, rather than as a complex. Using the obtained Phaser solution (two dimers of CDK2·Cyclin A), we performed Cartesian-simulated annealing using PHENIX.²⁰ The final refined model was obtained by iterating between manual real-space refinement in COOT²¹ and automated refinement in PHENIX. Early stages of refinement were dominated by manual rebuilding of the missing loops (residues 10–18, 37–42, and 153–166) using minimal refinement options, including reciprocal space atomic positions and individual atom isotropic B factors with default NCS restraints. NCS was applied between the two CDK2 chains, A and C, and the two cyclin chains, B and D. After the protein chains were well described by the refinement model, NCS B-factor restraint weights were reduced and TLS refinement was introduced. TLS groups were identified using the TLSMD server.^22,23 After protein modeling was completed, the ADP ligands were built into the electron density. Phosphates were positioned by placing the phosphorus atom at the center of the strong point of density in each identified phosphate region of the electron density. Following one round of refinement after ADP placement, the Mg²⁺ ions and coordinating waters were positioned in a similar manner. We used phenix.metal_coordination to maintain the proper coordination of the identified Mg²⁺ ions and coordinating groups. The additional restraints were necessary to prevent PHENIX from moving the coordinating groups out of the electron density, most likely due to repulsive nonbonded terms in the minimization function utilized by PHENIX. Finally, remaining ordered water molecules were identified by PHENIX (default water search options) and included in the final stages of structure refinement.

A kicked omit map was generated by removing the ADP, Mg²⁺, coordinating water atoms from the final ADP·2Mg model, and then computing a kicked mFo-DFc difference map.²⁴ To generate a kicked map a large ensemble of slightly perturbed models is generated by moving atoms randomly to varying degrees and then averaging maps using phases computed from those perturbed models.

Enzyme Kinetics and Solvent Viscosity Effect Studies

Kinase activity was measured using a coupled assay in which ADP production is linked to NADH oxidation using pyruvate kinase and lactate dehydrogenase (PK/LDH). In all experiments presented here, the protein substrate for pCDK2·Cyclin was histone H1. Since this work is focused on the nucleotide/Mg²⁺ interactions and since K_M(H1) does not change significantly as a function of [Mg²⁺]_free (Supporting Information, Figures 15 and 16), H1 is kept at a saturating level in all conditions (200 μM ≈ 10 × K_M(H1). H1 concentration was determined spectroscopically using ε₂₃₀ = 1.85 cm²/mg,²⁵ and ATP concentration was determined with ε₂₅₉ = 15 400 cm^–1 M^–1. Kinase reaction progress was monitored by absorbance at 340 nm with a spectromax plus 384 spectrophotometer. Reaction buffers included 100 mM Tris pH 7.5, 1 mM phosphoenolpyruvate, 280 μM NADH, and at least 60 and 90 units of PK and LDH, respectively. MgCl₂ and KCl were included in varying amounts to achieve the desired [Mg²⁺]_free, with a final ionic strength of 162 mM. Calculation of [Mg²⁺]_free assumes a K_D of ATP for the first Mg²⁺ [to form (ATP·Mg)^2–] of 28.6 μM.⁹ Binding of Mg²⁺ to other sources (K, Tris, other ATP species) was not considered in the [Mg²⁺]_free calculations for this work because the iterative Storer method indicates contributions from those sources were much weaker than the ATP·Mg interaction and result in a linear reduction of [Mg²⁺]_free over the ATP and Mg²⁺ concentration ranges considered herein.

The effect of solvent viscosity on CDK2 reactions was determined for sucrose solutions of 0, 150, 240, and 296 g/L. Relative viscosity was determined using η_rel = t°d°, where t° = t_Sucrose/t_NoSucrose, t is the mean flow time of the buffer in an Ostwalt viscometer measured 10 times, and d° is the relative density of the buffers. Reactions were performed with 25 or 50 nM kinase at 30 °C using preheated plates. All components of the reaction were mixed and preheated to 30 °C, and then the reaction was initiated by adding the kinase. Reaction rates were determined using the linear portion of the 340 nm absorbance trace. Rates of the lowest and highest [Mg²⁺]_free conditions at the lowest and highest sucrose conditions were linearly dependent on [CDK2·Cyclin]. PK/LDH, H1, and ATP·2Na were obtained from Sigma-Aldrich. The solvent viscosity effect reported in Figure 8 was calculated as the slope m of the line η_rel = m(v°/v) + intercept, where v° is the velocity with 0 sucrose (graphically a plot of v°/v vs η_rel). These data are included in the Supporting Information.

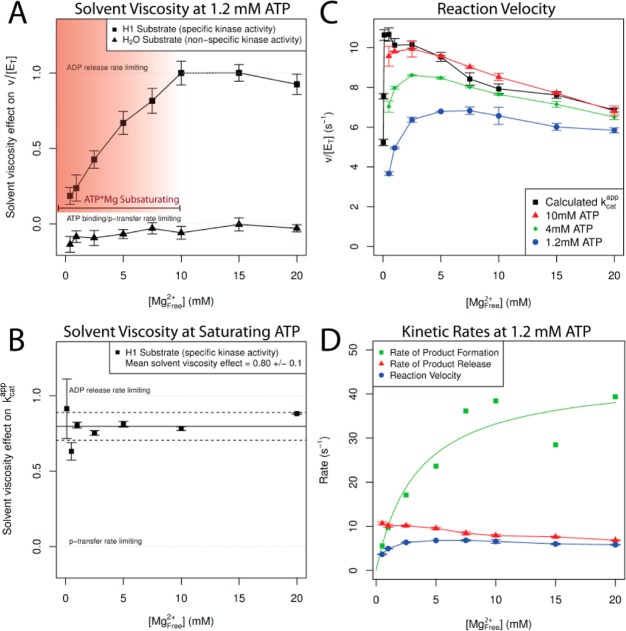
Figure 8.

Second Mg²⁺ activates ATP phosphoryl transfer and inhibits ADP release. (A) Solvent viscosity effect at 1.2 mM constant ATP. Kinase activity (200 μM [H1], squares) shows increasing dependence on product release as a function of [Mg²⁺]_free (0.5–20 mM). No solvent viscosity effect on the ATPase activity (water as substrate, 0 mM [H1], triangles) indicates that viscogen does not specifically inhibit CDK2 activity. (B) Solvent viscosity effect at saturating [ATP·Mg] and [H1] (see Supporting Information Figures 17–19) as [Mg²⁺]_free varied (0.1–20 mM). Solid line is the mean of the solvent viscosity effect vs [Mg²⁺]_free data points; dashed lines represent standard error. (C) pCDK2·Cyclin rate at 10 (red), 4 (green), and 1.2 mM ATP (blue) and k_cat (black), [Mg²⁺]_free varied from 0.5 to 20 mM. (D) Rates of product formation and product release at 1.2 mM ATP. Green squares shows that the net rate of substrate binding and chemistry is activated by [Mg²⁺]_free. Red triangles show the rate of product release is slowed by [Mg²⁺]_free. Blue circles are the total enzyme velocity at 1.2 mM ATP (same data in the blue curve of C). Rate of product release is equivalent to the black k_cat curve from C (data from Figure 3D) since the viscosity effect at saturating substrates in B is close to 1. Rate of product formation includes all steps of reaction required to form the products in the active site, including ATP·Mg binding, protein substrate binding, second Mg²⁺ binding, and phosphoryl transfer. Green square data points calculated as k_{product formation} = (k_{product release}k_obs(ATP1.2))/(k_{product release} – k_obs(ATP1.2)). Green curve is a hyperbolic fit to the green square data points. This curve should just be viewed as an estimate. Calculated standard error on the green squares would be very large because of the modest error on the measured rates compounds such that it is a significant portion of the denominator at high magnesium. We suggest that the trend in that data is correct because the viscosity effect from A ([ATP] = 1.2 mM) demonstrates that the rate of product formation is much faster than the rate of product release at high magnesium.

Isothermal Calorimetry To Measure Binding of ADP

Purified pCDK2·Cyclin was obtained as described in the Crystallography section. The calorimeter cell contained 25 μM protein buffered in 150 mM KCl, 5–10 mM MgCl₂, 5% glycerol v/v, and 25 mM HEPES pH 7.5. The syringe contained 5 mM ADP in the same buffer as in the cell. This experiment was performed at 20 °C with magnesium concentrations of 5, 7.5, and 10 mM [Mg²⁺]_Total in both the protein and ADP solutions. A concentration of 2.5 mM [Mg²⁺]_Total was attempted, but the signal was too low for accurate fitting. ITC data analysis was performed in the Origin software provided by MicroCal. Baseline correction was performed using the signal asymptote at high ADP:protein molar ratio. Curve fits were performed assuming a single-site binding model with ADP binding stoichiometry fixed to 1:1. Data can be viewed in Supporting Information Figures 1–3.

Molecular Dynamics

All molecular dynamics (MD) simulations were performed using the Amber99SB²⁶ force field using Amber10 for MD integration.²⁷ In addition to the base Amber99SB parameters, we used ADP parameters from Meagher et al.²⁸ and phospho-threonine parameters from Homeyer et al.²⁹ Parameters for protonated ADP were generated using the AMBER RESP protocol^30,31 based on a charge distribution generated in vacuo from HF 6-31G* geometry-optimized methyl-diphosphate in Gaussian03.³² The starting model for each simulation was prepared by selecting a single pCDK2·Cyclin A dimer from the crystallographic asymmetric unit (chains A and B). Next, the model was protonated and solvated in TIP3P explicit water³³ arranged in a truncated octahedral box with 150 mM explicit NaCl, plus additional ions for countercharge, using the Amber tleap software package. The simulation system was then minimized using successive rounds of conjugate gradient and then steepest descent minimization with successively reduced harmonic restraints on the protein. Next, the restrained system was slowly heated from 0 to 303 K over 30 ps of constant volume simulation. Switching to a constant pressure/constant temperature (NPT) ensemble, the system was then allowed to equilibrate with continually diminishing restraints over an additional 120 ps of system equilibration. Constant temperature and pressure were regulated by a Berendsen thermostat³⁴ and pressure by isotropic volume scaling, both with very weak coupling to the dynamics. All hydrogen atom bond lengths were constrained using SHAKE. Fifty nanoseconds of production dynamics were calculated for each trajectory using PMEMD (part of the Amber software package). Each starting conformation was equilibrated and simulated in five separate trajectories. For each trajectory, the initial bulk solvent ion positions were randomly exchanged with solvent molecule positions far (at least 5 Å) from the protein solute to decorrelate the separate trajectories. The time series and other MD analysis plots were prepared in the R statistical software package.³⁵

Results

Two Mg²⁺ Ions Are Required for Optimal CDK2 Kinase Activity

We previously reported the crystal structure of fully activated CDK2 (pCDK2·cyclin) bound to a transition state mimic (ADP·MgF₃·peptide). In this structure there was clear evidence for two catalytic Mg²⁺ ions in the kinase active site. Under conditions of constant ATP concentration a multiphasic dependence on Mg²⁺ concentration was observed that was most simply consistent with two essential Mg²⁺ ions.⁷ To further investigate the requirement for multiple catalytic Mg²⁺ ions we carried out a more complete steady state kinetic analysis of the kinase reaction using histone H1 as a substrate.

As the biological substrate of kinases is ATP·Mg²⁺, it can be difficult to separate out the contribution from this essential Mg²⁺ that is bound along with the substrate and the contribution of a second Mg²⁺ ion. However, the requirement for a second essential Mg²⁺ ion can be inferred from experiments in which the concentration of ATP substrate is varied at a constant total concentration of Mg²⁺ ions.^14,36 Under conditions in which the concentration of ATP is far above the K_D for dissociation of the ATP·Mg²⁺ complex (28.6 μM⁹), the added ATP will chelate 1 equiv of Mg²⁺, thereby depleting the concentration of free Mg²⁺ that is available. Consistent with our previous results, the effect of increasing ATP concentration is biphasic with a clear saturation of the velocity followed by a decrease in velocity as the concentration of free Mg²⁺ is depleted. At a higher concentration of total Mg²⁺ the inhibitory phase is shifted to higher concentration of ATP (Figure 3A). These data could be explained by a model in which ATP without Mg²⁺ is a potent inhibitor of CDK2 or by the model in which two Mg²⁺ are required for optimal activity. Below we present additional data in support of the model that CDK2 requires two Mg²⁺ ions for catalysis.

Figure 3.

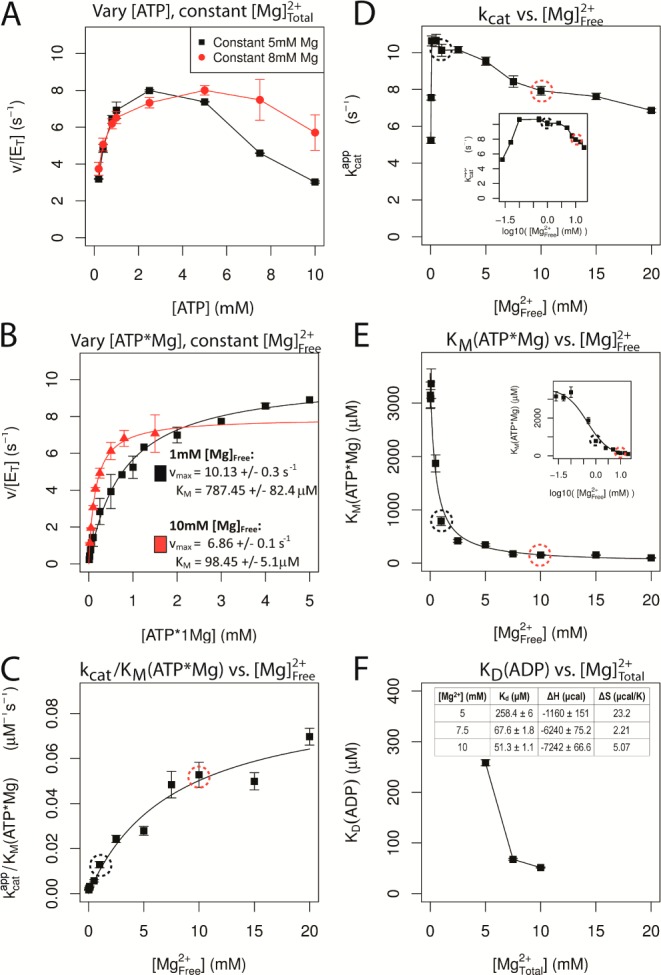
Cooperativity between nucleotide and Mg²⁺ binding to CDK2. (A) Dependence of the multiple turnover kinase reaction on the concentration of ATP at constant [Mg²⁺]_total. Histone substrate was saturating and kinase activity was measured using a coupled assay (see Experimental Methods for details). Concentration of total Mg²⁺ was fixed at either 5 or 8 mM. (B) Multiple turnover kinetics in which the concentration of ATP·Mg²⁺ was varied at a fixed concentration of either 1 (black) or 10 mM (red) free Mg²⁺. Velocity was fit by the Michaelis–Menten equation (lines). (C–E) Resulting steady state constants from these experiments and from data collected at additional concentrations of free Mg²⁺ (see Supporting Information Figures 4–14). (C) Value of k_cat/K_M^ATP·Mg was fit to a hyperbolic binding equation, indicating a very weak affinity of ∼10 mM for Mg²⁺ binding to free enzyme in the absence of nucleotide. (D) Value of k_cat shows a complex dependence on the concentration of free Mg²⁺ with a highly cooperative stimulation at very low Mg²⁺ and a modest decrease in k_cat between 1 and 20 mM Mg²⁺. Inset: log10 scale. (E) Value of K_M for ATP·Mg²⁺ is dramatically decreased by binding of a second Mg²⁺ ion. (F) Dissociation constant for ADP was determined by isothermal calorimetry as a function of total Mg²⁺ (see Supporting Information for details).

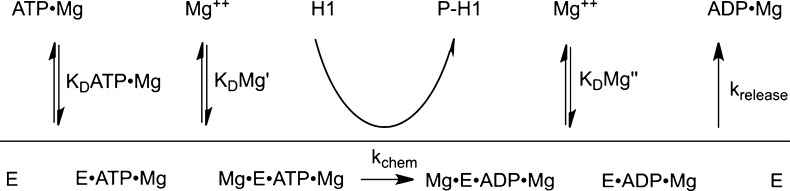
To more carefully examine the ATP utilization of CDK2 and the cooperativity between ATP·Mg²⁺ binding and the binding of the second catalytic Mg²⁺ ion we analyzed the steady state kinetics of CDK2 at varying concentrations of ATP·Mg²⁺ with fixed concentrations of free Mg²⁺. Under these conditions the substrate concentration dependencies followed simple Michaelis–Menten behavior (Figure 3B). When the concentration of ATP·Mg²⁺ was subsaturating (k_cat/K_M conditions), the affinity of the second essential Mg²⁺ ion for the free enzyme could be determined (Scheme 1). The resulting k_cat/K_M value gives a roughly hyperbolic or possibly linear dependence upon the concentration of free Mg²⁺, indicating very weak binding of the second Mg²⁺ in the absence of ATP·Mg²⁺ (Figure 3C). This provides strong additional support that the active form of CDK2 contains two Mg²⁺ ion cofactors (Scheme 1), and this behavior is not explained by the alternative model that ATP is an inhibitor of CDK2. The analogous plot of k_cat as a function of free Mg²⁺ shows a more complex behavior (Figure 3D), with an optimal rate obtained at 1 mM free Mg²⁺ and a gradually decreasing rate constant at concentrations above 1 mM. The cooperativity between binding of the ATP·Mg²⁺ and the second Mg²⁺ is apparent by the dramatic decrease in the value of K_M ATP·Mg²⁺ (Figure 3E). Taken together, these steady state kinetic data strongly support the proposed model that CDK2 requires two catalytic Mg²⁺ ions, and furthermore, the binding of the second Mg²⁺ ion is highly cooperative with the binding of the nucleotide and its accompanying Mg²⁺ ion.

Scheme 1. Proposed Kinetic Scheme at Saturating Protein Substrate Conditions.

Crystal Structures of pCDK2·Cyclin A in Complex with ADP Demonstrate Binding of Either 1 or 2 Mg

We structurally characterized the interaction between ADP and the kinase by determining and analyzing several new crystal structures of the pCDK2·Cyclin complex bound to ADP. Two representative structures are described here, each of which has a different conformation and divalent metal coordination for ADP. One structure has two Mg²⁺ ions coordinating the ADP phosphates (ADP·2Mg), and the other has only a single Mg²⁺ ion coordinating the phosphates (ADP·1Mg).

The overall structure of the pCDK2·Cyclin complexes crystallized is shown in Figure 2A. The protein conformation of the two new ADP-bound structures is similar, the ADP·2Mg structure and ADP·1Mg structure have a backbone rmsd of 0.20 Å. Both are also quite similar to other published CDK2·Cyclin structures. The backbone rmsd from ADP·2Mg structure to 1JST (a complex with ATPγS·Mn²⁺) = 1.24 Å, 1QMZ (AMPPNP·Mg²⁺/peptide) = 0.65 Å, 3QHR (ADP·2Mg/MgF₃^–/peptide TS) = 0.57 Å. Crystals formed in the P12₁1 space group with an asymmetric unit containing two copies each of CDK2 and Cyclin A (see Supporting Information Table 1 for crystallography statistics). Unlike other crystal forms of pCDK2·Cyclin, this crystal form grows in the presence of Mg²⁺ and has only been observed for pCDK2·Cyclin in our recently published transition state mimic structures (3QHR, 3QHW). The primary contact between pCDK2 and Cyclin A is along the canonical dimerization interface, which has an interface area of ∼1800 Ų (buried surface area of ∼3300 Ų). Remaining crystal contacts have significantly smaller contact surfaces, all of which comprise of less than 420 Ų each. Importantly, none of the crystal contacts occlude the active site or restrict the motion of the Gly loop in any obvious way. The lack of crystal contacts in the vicinity of the active site combined with the high solvent content (>60%) quite possibly makes this crystal form amenable to soaking ligands into the apo enzyme.

We soaked ADP into apo crystals of pCDK2·Cyclin A at a variety of magnesium concentrations for a range of soaking times. The two crystals presented here were prepared and soaked under very similar conditions. The ADP·2Mg and ADP·1Mg crystals were soaked with 3.2 mM ADP with 10 mM MgCl₂ and either 25 or 50 mM HEPES pH 7.5 for 1 h each. Because the crystallization condition contains 20 mM MgCl₂ and the soak has 10 mM MgCl₂, effectively titrating Mg²⁺ from the crystal, it is difficult to know what the precise final Mg²⁺ concentration is within each crystal. Because we observe different numbers of active site Mg²⁺ ions in different crystals prepared in such similar conditions, we believe that the effective Mg²⁺ concentration in the crystals must be close to the equilibrium binding constant for one of the magnesium ions, such that small differences in the ionic strength of the soak or crystal handling are sufficient to shift the phosphate–Mg²⁺ equilibrium between 2 or 1 Mg²⁺ bound per ADP.

We have high confidence in the positioning and occupancy of the ADP ligand because electron density in the active site allows for clear identification of all ADP atoms and coordinating groups. The kicked omit mFo-DFc difference map in Figure 2B shows the ADP electron density in the active site for the ADP·2Mg structure. In many ways, the coordination and geometry of the ADP in these structures is similar to the nucleotide coordination observed in other CDK2·Cyclin A crystal structures, most notably the geometry of the ADP in the TS mimic complex. At the same time, subtle differences between the phosphate coordination in the ATP, TS, and these two new ADP structures reveal additional details of the mechanism for phosphate binding, phosphoryl transfer, and product release.

Similar to most other structures of CDK2·Cyclin bound to nucleotide, the adenine rings of both the 1Mg- and the 2Mg-bound ADP are stabilized by a combination of specific electrostatic interactions with the protein backbone and hydrophobic interactions on either face of the nucleotide rings. The ribose 2′ and 3′ hydroxyls make electrostatic interactions with D88 and the carbonyl of N131. One α-phosphate oxygen atom is coordinated by the amine group of K33, which in turn is interacting with the carboxylate of E51 (Figure 4). The α- and β-phosphates are coordinated by the Mg²⁺ ion in the MgII site, and in the ADP·2Mg structure the β-phosphate is additionally coordinated by the Mg²⁺ ion in the MgI site. The Mg²⁺ ions are in turn coordinated by the CDK2 side chains of N132 and D145.

Figure 4.

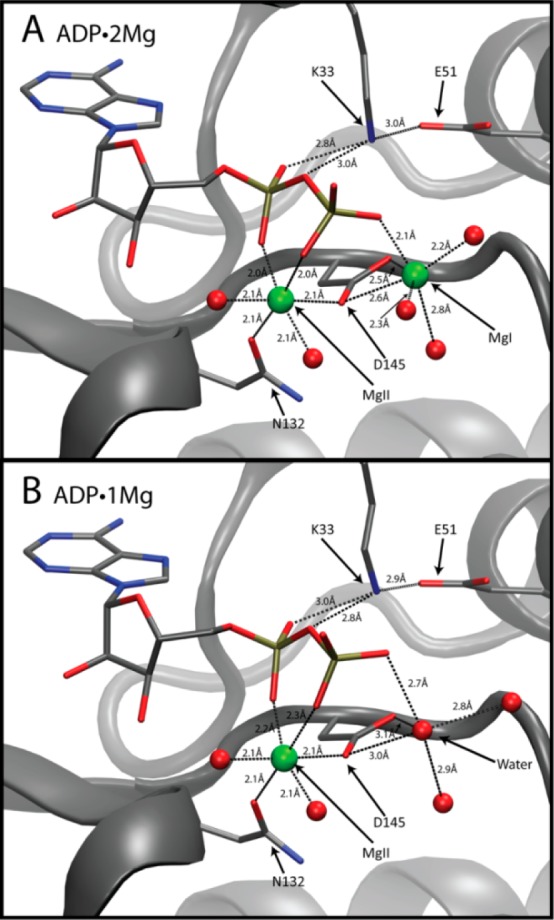
Phosphates and magnesium coordination. ADP, K33, E51, N132, and D145 drawn in stick representation. Green spheres depict Mg²⁺ ions. Red spheres represent water molecule oxygens. (A) ADP coordinated by two Mg²⁺ ions in the ADP·2Mg structure. (B) ADP coordinated by a single Mg²⁺ ion in the ADP·1Mg structure. Water occupies the MgI site in the ADP·1Mg structure.

Compared to the CDK2 TS-mimic structure (Figure 2D), which features ADP, MgF₃^–, two Mg²⁺ ions, as well as substrate peptide bound in the active site, we observe significant differences in the coordination of the ADP phosphates, resulting from a shift in the conformation of the Gly loop (CDK2 residues 12–18). The TS structure features a closed conformation of the Gly loop that is partially stabilized by catalytically important backbone amide interactions with both the nucleotide β- and γ-phosphates. In both of the ADP-only structures, the Gly loops have returned to the open conformation, also observed in some ATP analogue structures, where the Gly-loop residues are not participating in any direct interactions with the β-phosphate or the no longer present γ-phosphate. The Gly loop is positioned such that some ordered water molecules are identified mediating interactions between the ADP phosphates and the Gly loop, replacing the direct Gly-loop amide interactions with the β-phosphate oxygens present in the TS.

ADP·2Mg Crystal Structure

Figure 4A shows the coordination of the ADP phosphates in the ADP·2Mg structure. We labeled the two Mg²⁺ ions coordinating the ADP MgI and MgII, consistent with the cAMP-dependent kinase (PKA) established nomenclature.^15,37 We established the chemical identity of the magnesium ions using two criteria: (1) interatomic distances between the Mg²⁺ and its coordinating groups and (2) the octahedral coordination geometry.³⁸ The electron density of the coordination environments of both MgI and MgII can be seen in Figure 5A and 5B. The MgI site had not been occupied in structures of CDK2 until the recent TS structure (3QHR, 3QHW). It is possible that MgI had not been previously identified in CDK2 structures because many of the structures were prepared with lower magnesium concentrations (1–5 mM [Mg²⁺]_total) than was used in this work^3,4,39 or because they used nonhydrolyzable ATP analogues or alternative divalents with slightly different chemical properties.

Figure 5.

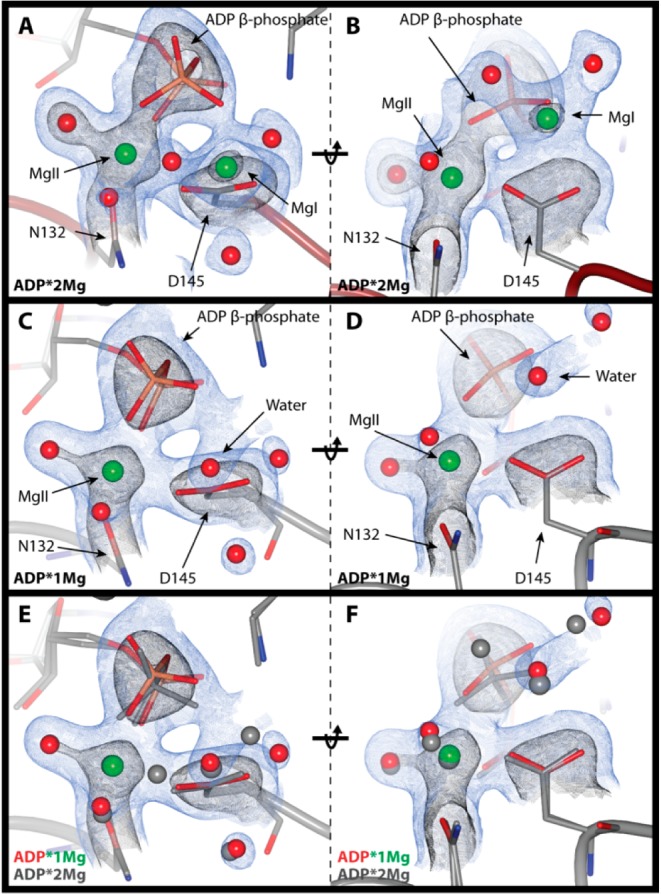
Phosphates and magnesium electron density. 2mFo-DFc electron density maps; blue contoured to 1σ and black to 2.5σ. Electron density clipped to within 2 Å of ADP β-phosphate, Mg²⁺ ions, and coordinating atoms or ordered waters occupying the MgI site in the ADP·1Mg structure. (Left) ADP β-phosphate coordination with Mg²⁺ ions. (Right) D145 coordination of Mg²⁺ ions (rotated 90° relative to left-side panels). (A and B) ADP·2Mg structure. (C and D) ADP·1Mg structure. (E and F) Comparison of ADP·1Mg and ADP·2Mg structures. ADP·1Mg electron density is shown, ADP·1Mg atoms are in color, and ADP·2Mg atoms are in gray. The ADP β-phosphate is rotated away from D145 in the ADP·1Mg structure relative to the ADP·2Mg structure.

MgI is located in nearly the identical position as it is in the TS structure. MgI is coordinating the β-phosphate of ADP and participates in a bidentate interaction with both oxygens of D145, and its 6-fold coordination is rounded out with three bound water molecules. As in the TS structure, the coordination geometry of MgI deviates from an ideal regular octahedron because the simultaneous coordination of the two D145 carboxylate oxygens results in a 51° angle rather that the ideal 90° O–Mg–O angle. In this ADP-bound structure, the position occupied by one of the fluorine atoms of the γ-phosphate mimic from the TS structure is replaced by a water molecule positioned 2.2 Å from MgI.

The coordination of MgII is also very similar to the TS structure. MgII interacts with the α- and β-phosphates of ADP (one oxygen each). Additionally, MgII is coordinated by one oxygen each of CDK2 residues D145 and N132. Finally, there are two ordered water molecules interacting with MgII to complete the regular 6-fold octahedral coordination for magnesium. Similar to MgI, one of these ordered water molecules replaces a γ-phosphate mimic fluorine found in the TS structure. Thus, transfer of the γ-phosphate results in the binding of one additional water to each of the two Mg²⁺ ions at positions formerly occupied by γ-phosphate oxygens in the TS.

ADP·1Mg Crystal Structure

The phosphate and magnesium ion coordination for the ADP·1Mg structure is shown in Figure 4B. In this structure MgI is no longer bound to the pCDK2·Cyclin·ADP complex while MgII remains clearly defined. We conclude that MgI is not bound to the ADP·1Mg crystal in any significant population because the electron density of the ADP·1Mg structure in the vicinity of MgI (Figure 5C and 5D) is quite different than that of the ADP·2Mg structure (Figure 5A and 5B). There is some electron density in the bisector of the D145 carboxylate, but the distance from the center of this density to each carboxylate oxygen atom is greater than that of the ADP·2Mg structure: the distances increased from 2.5 to 3.0 Å. The distance to the nearest β-phosphate oxygen is also too long for proper magnesium coordination, 2.7 Å (compared to 2.1 Å in the ADP·2Mg structure). Finally, density for one of the water molecules coordinating MgI in the ADP·2Mg structure is not present. The electron density in this structure is thus strongly inconsistent with the presence of a divalent Mg²⁺ ion occupying the MgI site and much more consistent with the presence of either an ordered water molecule or perhaps a monovalent sodium ion.

A comparison of the ADP·2Mg and ADP·1Mg structures can be seen in Figure 5E and 5F. Figure 5E highlights how the β-phosphate coordination differs between the two structures. The β-phosphate is rotated closer to MgI in the ADP·2Mg structure than in the ADP·1Mg structure. Furthermore, the ADP·2Mg structure has clear density for two water molecules coordinating MgI.

Molecular Dynamics Simulations: ADP·2Mg Is More Rigid than ADP·1Mg

In our earlier structures and MD simulations of the phosphoryl transfer step⁷ we found that the binding of the second magnesium (MgI) to the ATP·1Mg-bound active site alters the coordination of the phosphates (Figure 2C and 2D) as well as restricts their flexibility to resemble the TS conformation. Comparing the ADP·2Mg structure to the ADP·1Mg structure, differences in the electrostatic coordination of the β-phosphate suggest that coordination by two Mg²⁺ ions may similarly restrict the flexibility of the ADP–phosphates more than coordination by a single Mg²⁺ ion. To examine how the Mg²⁺ coordination affects the conformational variability of the phosphates and the dynamics of the ADP interactions with CDK2, we performed a series of MD simulations of the ADP·2Mg and ADP·1Mg structures, summarized in Supporting Information Table 2. Because we cannot establish protonation states or confidently distinguish a water molecule from a sodium ion at our present resolution, we also simulated a number of alternative protonation states and Na/H₂O assignments that could be the best representations of our current crystal structures.

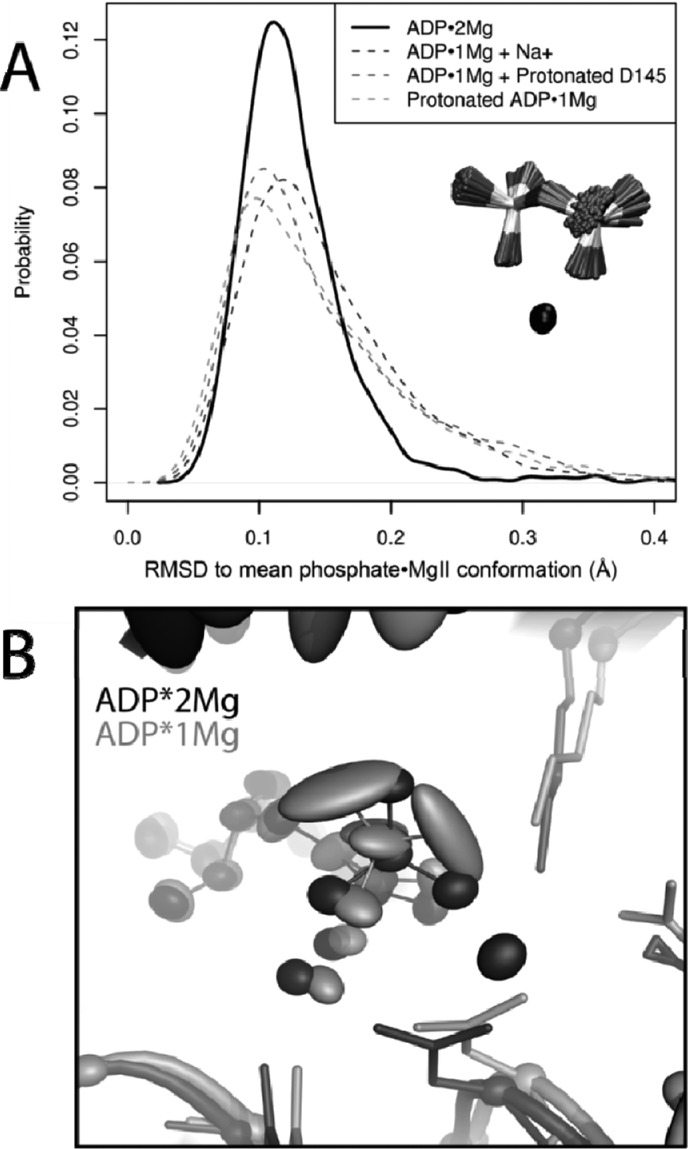
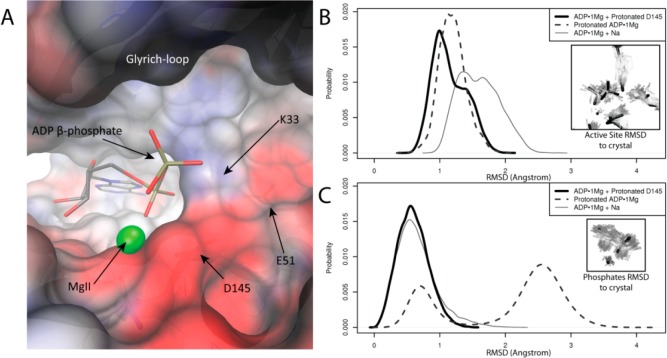
We measure the flexibility of the phosphates by considering the rms fluctuations of just the phosphates and MgII about their mean conformation in the last 30 ns of each trajectory. By superimposing trajectory structures on only the phosphorus and MgII atoms alignment-dependent contributions from motion of the kinase domain are avoided. As in Figure 6A, the ADP·2Mg trajectories sample conformations similar to their mean conformation more frequently than any of the ADP·1Mg-type simulations. This is indicated by the reduced spread of the ADP·2Mg distribution of rms fluctuations. The ADP·1Mg-type simulations have long tails extending into higher rms fluctuations, indicating they sample a broader range of conformations than the ADP·2Mg simulations. Thus, the phosphates are more flexible when coordinated by a single Mg²⁺ ion.

Figure 6.

Second Mg²⁺ decreases ADP motion. (A) rms fluctuations of ADP phosphates and MgII in ADP·2Mg and ADP·1Mg-type MD simulations. Phosphorus atoms and MgII were aligned in each trajectory; fluctuations about the mean conformation describe motion of just phosphate·MgII atoms. ADP·2Mg simulations show less phosphate flexibility than ADP·1Mg-type simulations. (B) Comparison of two representative simulations: ADP·2Mg (black) and ADP·1Mg + Protonated D145 (gray). Ellipsoids represent 50% probability position of atom position relative to the CDK2 domain mean position. Phosphate oxygens in ADP·1Mg-type simulations are more mobile than phosphate oxygens in ADP·2Mg simulations.

Figure 6B shows how the increased flexibility of the ADP·1Mg phosphates corresponds to greater positional variance in the active site relative to the more restrained ADP·2Mg phosphates when the trajectories are aligned on the kinase domain. The decreased mobility of the ADP·2Mg phosphates relative to the phosphates in any of the ADP·1Mg models is consistent with increased electrostatic stabilization afforded by two Mg²⁺ ions.

Cooperativity between Magnesium and ADP Binding

The combination of the partial occupancy of Mg²⁺ binding at the MgI site with the complex rate dependence of CDK2 kinase activity on magnesium concentration (Figure 3) prompted us to examine the effect of Mg²⁺ concentration on the energetics of ADP binding. We measured the affinity of pCDK2·CyclinA for ADP as a function of magnesium concentration using isothermal titration calorimetry (ITC). The dissociation constants of ADP at 5, 7.5, and 10 mM [Mg²⁺]_Total are shown in Figure 3F. As the concentration of magnesium increases, the dissociation constant of ADP binding to CDK2 decreases. We did not obtain a measurable ITC signal at 2.5 mM [Mg²⁺]_Total, which we interpret as even weaker or no binding of ADP at lower [Mg²⁺]_Total. Consistent with the predicted electrostatic stabilizing effect of Mg²⁺ binding, the favorable enthalpy of ADP binding becomes larger at higher [Mg²⁺]_Total.

The partial occupancy of the MgI site across crystal structures suggests that the positive cooperativity between ADP·Mg and Mg²⁺ binding to the enzyme can be explained by increased Mg²⁺ binding to the MgI site. The MgII site is always occupied when ADP is bound. While the crystal structures help illuminate the origin of the Mg:ADP cooperativity, it is important to note that the ∼10 mM [Mg²⁺]_total and 3.2 mM ADP present in the crystal conditions are not intended to reproduce physiological concentrations. In many cell types the available (“free”) intracellular Mg²⁺ concentration is close to 1 mM (although the total [Mg²⁺] is often greater than 20 times that amount).⁴⁰ Intracellular [ADP] is extremely low due to the activity of enzymes like pyruvate kinase and adenylate kinase, and so under these conditions the only AnP nucleotide binding species will be ATP·Mg. Thus, any bound ADP must originate from the phosphoryl transfer reaction and will initially be bound to the active site with both of the two catalytically essential Mg²⁺ ions. For these reasons, a key question we address throughout the remainder of this work is how does the cooperative ADP:Mg interaction with CDK2·Cyclin affect the overall activity of the enzyme under physiological concentrations?

Glycine-Rich Loop

To continue our investigation of the progression of the catalytic cycle, we next examine how the kinase transitions from the TS-mimic conformation with a closed Gly loop to the ADP-bound state that exhibits an open Gly loop. In our previous work, MD simulations of pCDK2·Cyclin with ATP and two Mg²⁺ ions (“ATP·2Mg”) and ATP with one Mg²⁺ ion (“ATP·1Mg”) reproducibly showed that the Gly loop spontaneously closes to a conformation similar to the TS state when ATP is coordinated by two Mg²⁺ ions but not when ATP is coordinated by a single Mg²⁺. In simulations of the two-Mg TS, the Gly loop remains closed and does not open. From this we concluded that binding of the second Mg²⁺ ion to an ATP·Mg²⁺-bound CDK2 complex stabilizes the closed Gly-loop conformation (“Gly-down”), thus contributing to stabilization of the TS that accelerates phosphoryl transfer.

Unlike with ATP, simulations of ADP·2Mg- or ADP·1Mg-bound CDK2 find that the presence of two Mg²⁺ ions does not result in spontaneous closing of the Gly loop when ADP is bound. This confirms the stability of open Gly-loop conformations observed in the crystal structures of ADP·2Mg and ADP·1Mg and suggests the presence of the γ-phosphate, in addition to the two Mg²⁺ ions, is required to stabilize the closed conformation of the Gly -loop. To see how the Gly-loop transitions from closed to open following phosphoryl transfer and if there is a significant barrier to this transition, we carried out a series of MD simulations starting with the Gly-down conformation of the kinase and either ADP·2Mg or ADP·1Mg in the active site. In the closed Gly-loop conformation, Gly-loop amides are within hydrogen-bonding distance of the β-phosphate, but the open Gly loop is free to sample many different conformations. When open, a layer of water forms between the β-phosphate and the Gly loop, breaking the direct interactions between the Gly-loop amides and the β-phosphate and increasing the distance between the β-phosphate and the Gly loop. We classify the position of the Gly loop by measuring the minimum distance between the β-phosphate oxygens and the Gly-loop amides and counting the number of waters within 4 Å of the β-phosphate. We define a closed Gly loop as being within H-bond distance (3 Å) of the β-phosphate oxygens and having no more than 4 waters near the β-phosphate. Greater distances and numbers of waters indicate an open Gly loop.

As shown in Supporting Information Figure 23, ADP·2Mg-Gly-down simulations the Gly loop opens within the first 4 ns of each simulation and remains open for the duration of the 50 ns trajectories. The ADP·1Mg-type Gly-down simulations are not as easily interpretable, because in some the Gly-loop opens and in others it remains closed. In the ADP·1Mg-type Gly-down trajectories in which the Gly loop does open it opens more slowly (takes up to 10 ns to open) than in the ADP·2Mg Gly-down trajectories. This implies that the presence of two Mg²⁺ ions contributes to the opening of the Gly loop after the γ-phosphate is transferred. Opening of the Gly loop may make a significant contribution to efficient release of ADP because the opening of the Gly loop increases the solvent accessibility of the phosphates.

Electrostatic Deficit in the ADP·1Mg Structure

The phosphate-binding portion of the active site has a strongly electronegative potential generated by the proximity of D145 and other residues in the active site, as shown in the APBS calculation⁴¹ in Figure 7A. The electrostatic potential shown was calculated for an “apo” structure in which the ADP·Mg and all solvent molecules were removed from the model. This means that the surface potential shown is what is “felt” by a ligand bound (or binding) to the surface shown. The charged residues in the active site, K33, E51, and D145, have a net charge of −1e. Assuming that the binding ADP species is trianionic, addition of ADP^3– and two Mg²⁺ neutralizes the charge in the active site in the ADP·2Mg structure, while the ADP·1Mg structure has a −2e net charge in the active site. In this scenario, the strong electronegative potential near the MgI site means that MgI binding is electrostatically favorable, neutralizing the overall charge in the active site.

Figure 7.

Electrostatic deficit in ADP·1Mg structure. (A) pCDK2·Cyclin A active site shows strong electronegative potential around the phosphate binding region. Electrostatic potential was calculated on the apo structure (ADP, Mg²⁺, and ordered solvent molecules removed from ADP·1Mg structure). Surface colored from −8 (red) to 8 k_bT/e^– (blue). ADP and magnesium are shown for reference. β-Phosphate interaction in active site less favorable with the MgI site unoccupied. (B) MD simulation: distribution of rms deviations of phosphates, MgII, and active site residues K33 and E51 from ADP·1Mg crystal structure for each of the ADP·1Mg-type simulations. Protonation of D145 or the β-phosphate sample lowers rmsd to the crystal more than Na⁺ binding. (C) MD simulation: distribution of rms deviations of just phosphates and MgII from the ADP·1Mg crystal structure for each of the ADP·1Mg-type simulations. Protonation of D145 reproduces phosphate coordination in the ADP·1Mg structure better than β-phosphate protonation or Na⁺ binding. Mode at 2.7 Å (protonated ADP simulation) corresponds to alternate phosphate positioning and is consistent with some weak electron density from ADP·1Mg crystal.

In the ADP·1Mg crystal structure, the electron density in the electrostatic deficit region was difficult to model, possibly due to the heterogeneity of bound species within the crystal. We opted to model three tightly packed water molecules in this region of the ADP·1Mg structure, as this model makes the fewest assumptions about a difficult to build region, though the mFo-DFc difference map indicates other models may also be consistent with the observed density.

To test alternative models of the ADP·1Mg structure, we carried out a series of molecular dynamics (MD) simulations of different configurations in the active site of pCDK2·Cyclin, summarized in Supporting Information Table 2. Simulations of the ADP·1Mg structure reproducibly observe the spontaneous binding of a sodium ion from the bulk solvent into the active site near the MgI site. Once the sodium ion binds it is not observed to leave the active site in the time scale of these simulations (50 ns). The binding of this monovalent ion is thus a nonequilibrium event in these simulations that functions to partially alleviate the electrostatic deficit and bring the system to a more stable state. Despite remaining in the active site, the bound monovalent is mobile within the active site and occupies many different positions in the electrostatic deficit region.

Alternative mechanisms for alleviating the electrostatic deficit in the ADP·1Mg structure include protonation of either the ADP β-phosphate or D145. We therefore tested three additional models of the ADP·1Mg active site: (1) Na⁺ positioned near the MgI site from the beginning of the simulation (“ADP·1Mg + Na”), (2) D145 protonated (“ADP·1Mg + Prot D145”), and (3) the β-phosphate protonated (“ProtADP·1Mg”). Each of these models leaves the active site with a net −1e charge, but because the nature of the charge distribution in the active site is disperse and not concentrated onto the phosphates or any particular residue in the active site (see Figure 7A) and because the region is somewhat solvent accessible, the remaining electronegative charge may be permissible.

The advantage of using MD simulations to test these models is that the ADP·1Mg crystal structure does not directly report on any features that allow definitive discrimination between these three models. We cannot identify an ordered monovalent in the ADP·1Mg crystal structure, suggesting that if a monovalent does bind it is delocalized, consistent with the results from the MD. If either the ADP phosphates or D145 is protonated, the electron density cannot help in discriminating between these models because protons do not contribute strongly to the electron density at 2.0 Å resolution.

ADP·1Mg Model: Protonation or Cation Binding?

We performed 50 ns equilibrium MD simulations of each of the ADP·1Mg models to investigate their plausibilities. The metric we used to assess the validity of each model is the ability of the simulation to reproduce the coordination of the ADP phosphates observed in the ADP·1Mg crystal structure. The distribution of rms deviations of the phosphates and coordinating active site residues K33 and E51 is shown in Figure 7B. The protonated D145 and protonated β-phosphate models both maintain active site coordination better (i.e., lower rms deviations) than the sodium-bound model. In Figure 7C, only the phosphates are included in the rms deviation calculation, thus only reporting on the position of the phosphate atoms relative to the crystal structure. The protonated D145 model best reproduces the crystal structure; however, the protonated β-phosphate model samples two different conformations of the phosphates, with the lesser occupied peak corresponding to the crystal structure. The second peak, ∼2.7 Å rmsd from the crystal conformation, corresponds to an alternate conformation of the phosphates in which the protonated phosphates break away from K33 and instead interact with the carbonyl of E13. The protonated β-phosphate position in this alternate conformation may account for some delocalized electron difference density in the ADP·1Mg crystal structure too weak for modeling an alternate conformation.

While the protonated-D145 simulations clearly reproduce the crystal structure better than the other models simulated, protonation of D145 is also the least chemically feasible model because the pK_a of an aspartic acid in solution is 4 whereas the pK_a of an ADP phosphate is 6.8, meaning that phosphate protonation is more likely at physiological pH. It is possible that the environment of the CDK2 active site shifts the pK_a of D145 in the ADP·1Mg-bound state (i.e., when the phosphates are present but with no occupancy of the MgI site) because of the electrostatic deficit generated by the close proximity of the β-phosphate, D145 and E51. PROPKA2⁴² predicts that the pK_a of D145 is shifted to 9.5 in the ADP·1Mg structure. What is clear from these simulations of the ADP·1Mg structure is that some type of countercharge needs to be introduced into the CDK2 active site to maintain the phosphate coordination of the ADP·MgII complex. It is possible that many different species are present in the ADP·1Mg crystal, and it is likely that the ADP·1Mg-bound state is transient and only quasi-stable on the pathway to ADP release. These results also suggest that changes in pH (especially to lower pH values) could likely alter the charge balance and electrostatic deficit within the active site and might even alter the stability of the Mg²⁺ ions within the active site.

Rate of ADP Release Is Rate Limiting and Becomes Slower at High Concentration of Mg²⁺

The decreased kinase activity that is observed at high [Mg²⁺]_free (Figure 3D), together with the cooperative binding of ADP·Mg²⁺ to CDK2·cyclin A (Figure 3F), suggests that the rate of ADP·Mg²⁺ release is rate limiting under these conditions. To investigate this possibility, we measured the solvent viscosity effect as a function of free Mg²⁺ concentration. Solvent viscosity effects have previously been determined for pCDK2·Cyclin (only at a single Mg²⁺ concentration) as well as other kinases to determine the relative contribution of product release to the overall reaction turnover.^5,8,43,44 Increased solvent viscosity will selectively slow the diffusive steps of the reaction while not affecting the nondiffusive steps. This experiment reports on the relative contribution of the rate of product release in determining the overall reaction rate for CDK2.⁸ The relative viscosity effect at a given condition is expressed as a number between 0 and 1, which indicates the contribution of product release to the overall rate. A value of 1 indicates the reaction is fully limited by product release, and a value of 0 indicates that product release is not rate limiting (some other step is much slower than product release).

The solvent viscosity effect on the observed steady-state velocity for both the basal ATPase activity (water as the phosphate acceptor) and the kinase activity (saturating histone H1 as the acceptor) was measured with 1.2 mM ATP at concentrations of free Mg²⁺ that varied between 0.4 and 20 mM (Supporting Information Figures 20 and 21), and the results are summarized in Figure 8A. The lack of a solvent viscosity effect for the ATPase reaction confirms the previous finding that ATP cleavage is rate limiting in the absence of a protein acceptor and that sucrose does not inhibit or alter the structure of CDK2.^5,43

At high [Mg²⁺]_free (H1 acceptor) the solvent viscosity effect is close to 1.0, indicating that product release is almost fully rate limiting. However, as [Mg²⁺]_free is reduced below 10 mM the solvent viscosity effect steadily decreases. This indicates that the identity of the rate-limiting step changes as a function of Mg²⁺ concentration. The reason for this change is that 1.2 mM ATP·Mg is not fully saturating when free [Mg²⁺] drops below 10 mM (Figure 3E), resulting in suboptimum phosphoryl transfer throughput. Although ATP·Mg saturates with a K_M value of ∼0.1 mM when [Mg²⁺]_free is 20 mM, the binding of the second essential Mg²⁺ ion is highly cooperative with ATP·Mg²⁺ binding (e.g., K_M for ATP is 3.4 mM when [Mg²⁺]_free is 0.1 mM). Effects of the positive cooperativity between ATP·Mg²⁺ and Mg²⁺ ion binding to the MgI site can be observed by titrating free Mg²⁺ at fixed concentrations of ATP·Mg, as shown in Figure 8C.

At all concentrations of ATP shown in Figure 8C we observed a 10–20% decrease in the kinase velocity at high [Mg²⁺]_free (most apparent high [ATP]) that is not due to an effect on the coupled reporter assay (data not shown). To determine if this inhibitory effect can be isolated to the product release step, we measured the solvent viscosity effect with saturating ATP at a range of [Mg²⁺]_free. Figure 8B shows that under saturating ATP·Mg and histone H1, the viscosity effect is both close to one and invariant as a function of [Mg²⁺]_free, indicating that product release is always rate limiting. Because product release dictates the overall reaction rate here, we can conclude that the origin of the inhibitory Mg²⁺ effect at high [Mg²⁺]_free (Figures 3D and 8C) can be isolated to an Mg-dependent reduction in the rate of product release. We suggest that increased [Mg²⁺]_free specifically slows the rate of ADP·Mg release (rather than phospho-protein) given the cooperativity between ADP·Mg and the second Mg²⁺ binding, and because the rate of ADP release is much slower than the rate of phosphorylated-protein product release in other protein kinases.⁴⁵

Discussion

While the recruitment of Mg²⁺ ions into the active site of CDK2 kinase is absolutely essential for catalysis, these Mg²⁺ ions have multiple effects and their combined consequences are complex. Integration of the structures of CDK2 bound to ADP and either one or two Mg²⁺ ions, along with the associated [Mg²⁺] dependence of ADP binding, and the dominant role that product release can play in determining enzyme turnover enables extension of our model for the roles that dynamic magnesium binding plays in the CDK2 active site beyond its effects during the phosphoryl transfer step. An understanding of the unavoidable link between the activating, limiting, and inhibitory effects of the Mg²⁺ ions allows us to more completely explain the complex effects of [Mg²⁺]_free on the overall rate of enzyme turnover.

The TS mimic structure of the phosphoryl transfer step demonstrated how the binding of the second Mg²⁺ ion to the kinase·ATP·Mg²⁺·substrate active site promotes phosphoryl transfer by closing the Gly loop, electrostatically/electronically stabilizing the TS relative to the reactants and optimizing the reactant geometry for catalysis.⁷ This new work illustrates that although the second Mg²⁺ ion is essential for the most efficient acceleration of the phosphoryl transfer step, the increased stability of the ADP product resulting from two Mg²⁺ ions in the active site also functions to slow the rate of ADP release. Release of ADP·1Mg is faster than release of ADP·2Mg. The structural similarities between the TS mimic and the ADP·2Mg structures, along with the relatively reduced active site fluctuations of both the 2Mg-bound TS and ADP MD simulations relative to the 1Mg ATP or ADP simulations, suggest a nearly symmetric active site assembly–disassembly process. The slow ADP off rate can therefore be thought of as the slow reversal of the cooperative assembly of the active site that facilitated stabilization of the transition state. Conditions that favor faster cooperative assembly of the TS (i.e., saturating substrates and high [Mg²⁺]_free) conversely result in a slower disassembly of the highly similar ADP·2Mg product state. This is important because the solvent viscosity experiments at saturating ATP·Mg and protein substrates demonstrate that even at physiological concentrations of Mg²⁺_free release of ADP·Mg from the active site limits the overall rate of the reaction.

The 2Mg TS mimic structure has a closed Gly loop, while the ADP·1Mg and ADP·2Mg structures of pCDK2·Cyclin are both observed to have an open Gly loop. This suggests that the open form of the Gly loop is energetically preferred for the ADP-bound kinase following phosphoryl transfer in the absence of the phosphorylated product. Our MD simulations starting from the “Gly-down” conformation of the CDK2·Cyclin complex confirm this, indicating that even when the ADP is coordinated by two Mg²⁺ ions the Glycine-rich loop readily opens well within the 50 ns simulation time frame. We conclude from these simulations and our previous TS structure and simulations⁷ that although the binding of the second Mg²⁺ (to the MgI site) of CDK2·Cyclin·ATP·Mg results in Gly-loop closure, once the ATP γ-phosphate is transferred and the phospho product released, the open conformation of the Gly loop becomes the most stable conformation, even with the continued coordination of ADP by two Mg²⁺. This differential stability is readily explained by the loss of stabilizing interactions between the γ-phosphate and the Gly-loop amides in the ADP-bound state. Furthermore, the open conformation of the Gly loop observed in both the ADP·2Mg and the ADP·1Mg structures may be an important intermediate along the pathway of ADP release because there is sufficient space for a layer of water to occupy the space between the phosphates and the Gly loop. Solvent accessibility of the phosphates is likely to promote release of the phosphates from the active site because of the loss of tight electrostatic coordination of the phosphate oxygens.

Although the stabilization or acceleration of Gly-loop opening by two bound Mg²⁺ ions may help enable ADP release, high concentrations of Mg²⁺ will still slow the rate of ADP release due to the stabilizing electrostatic effect of the two bound divalent ions. This inhibitory effect can be somewhat minimized at physiological [Mg²⁺]_free by the conclusion, based on the ADP·1Mg and ADP·2Mg crystal structures, that the occupancy of the MgI site is less than 100% even at concentrations of free Mg²⁺ as high as the 10 mM concentration present in our ADP·1Mg structure. Less favorable occupancy of the MgI site is also consistent with the observation that the electron density for MgI is slightly weaker than MgII in the ADP·2Mg structure. It is also possible that the ADP·1Mg crystal had some small population of protein molecules in which both Mg’s are bound, but it is not the dominant population because there is no clear electron density for MgI or its coordinating groups. Our interpretation is that Mg²⁺ binding to the MgI site is less thermodynamically stable than to the MgII site. On the basis of the ADP titration experiments (Figure 3F), we estimate the K_D of the MgI site in the ADP·1Mg -bound kinase is roughly 5–7 mM. Given that ADP is bound to a single Mg²⁺ in solution (ADP^3-·Mg²⁺K_D ≈ 400 μM) and that our structures and simulations suggest that the occupancy of the MgII site is preferred to the MgI site, we conclude that the MgII site will remain occupied in the kinase active site as long as the ADP is bound. The relative stability of the MgII site over the MgI site in the ADP·1Mg state is also consistent with the observation that the MgI site has never been occupied in structures of CDK2 bound to ATP or ATP analogues.

Examining the electrostatic characteristics of the pCDK2·Cyclin active site and the MD simulations of four different interpretations of the ADP·1Mg structure, we find that the electrostatic deficit generated by the close proximity of the ADP phosphates to the similarly electronegative active site residues requires introduction of some positive countercharge to reproduce and maintain the conformation and coordination of the ADP phosphates observed in the ADP·1Mg crystal structure. This is not necessary for the ADP·2Mg state because occupancy of the MgI site satisfies the −2e active site electrostatic deficit by completely neutralizing the active-site charge. We suggest that the various mechanisms of introducing a +1e charge into the ADP·1Mg active site, including protonation of the ADP β-phosphate or D145 or localization of a monovalent cation, can also stabilize ADP phosphate binding and the population in solution (and the ADP·1Mg crystal) likely includes some equilibrium between these states. However, because the +1e states only partially alleviate the total electrostatic deficit they cannot stabilize ADP binding to the same extent as MgI and thus may represent an ensemble intermediate step prior to release of the ADP·Mg. It should be noted that changes in pH or salt concentration are likely to alter the population of +1e states and potentially result in environmental (salt/pH) dependent changes in ADP stability as well as MgI affinity to the ATP·1Mg complex.

Since K_M(ATP·Mg) varies as a function of [Mg²⁺]_free (Figure 3E), cellular conditions are unlikely to always be saturating for ATP·Mg consumption by pCDK2·Cyclin. The results of the solvent viscosity experiment vs [Mg²⁺]_free at 1.2 mM ATP (Figure 8B) clearly illustrate the origins of the opposing activating and inhibiting effects of [Mg], both of which, we propose, can be specifically linked to Mg²⁺ binding to the MgI site. At this concentration of ATP, the relative viscosity effect (influence of ADP release) is close to zero at low [Mg²⁺]_free and then increases as a function of [Mg²⁺]_free. This indicates that the release of product only begins to dominate the overall reaction rate as [Mg²⁺]_free becomes significantly higher than the physiological value of 1 mM. We propose that the origin of this phenomenon is the strong cooperativity between the ATP·Mg substrate K_M and the second Mg²⁺ activator. The productive assembly, activation, and bond cleavage of the ATP·2Mg substrate dominates the overall reaction rate at lower concentrations of either ATP·Mg or Mg²⁺_free because progression through phosphoryl transfer under these conditions is slower than the rate of ADP release. As [ATP·Mg] and [Mg²⁺]_free are increased to saturating concentrations (values that are codependent due to their cooperativity), the rate of productive ATP·2Mg activation and phosphoryl transfer increases and the overall reaction rate transitions to become limited by the rate of ADP release. The opposing K_M(ATP·Mg) activating and ADP release inhibitory effects of [Mg²⁺]_free are further illustrated in Figure 8D, where we calculated the apparent rates of product formation (everything up to and including phosphoryl transfer) and product release as a function of [Mg²⁺]_free. The structures predict that the Mg²⁺ activator effect arises from the second Mg²⁺ binding to the MgI site along with ATP·1Mg and the Mg²⁺ inhibitor effect arises from product stabilization resulting from Mg²⁺ occupancy of the MgI site of the ADP·2Mg-bound enzyme.

Because the affinity of the second Mg²⁺ site when ADP·Mg is bound is weaker than the physiological 1 mM [Mg²⁺]_free and product release dominates the reaction rate when there are saturating substrates, the notable decrease in the overall rate of enzyme turnover at high Mg²⁺ concentrations is readily explained by increased population of the high-affinity ADP·2Mg state. The viscosity effect experiments at subsaturating ATP·Mg (but still saturating protein substrate) (Figure 8A) highlight the important limit that the ADP release rate imposes on the maximum possible turnover rate of the enzyme. Tuning the affinity of the second Mg²⁺ site higher through evolution might be predicted to increase the rate of product formation under conditions of lower [ATP·Mg] substrate, but this strategy would also be predicted to result in even slower ADP release and lower overall enzyme activity in the absence of additional changes that counteract this effect. In the case of CDK2, optimum enzyme activity has not been the only selective pressure; it must also be a highly regulated signaling switch, so perhaps further tuning under different selective pressure could evolve a more active CDK2. This process may describe some oncogenic CDK2 mutants.

Conclusions

Given that the binding of a second Mg²⁺ ion increases CDK2 binding affinity for ADP but only a single Mg²⁺ ion is required for ADP to remain bound, our hypothesis is that the energetically preferred reaction pathway for ADP release is for MgI to be released prior to release of the ADP·MgII complex. Two Mg²⁺ ions are essential for chemistry, so ADP·2Mg is the state following phosphoryl transfer and ADP·1Mg is the kinetically preferred intermediate along the pathway to ADP release. This is consistent with a similar result from a computational study of Protein kinase A (PKA) which concluded that release of ADP from that kinase with two Mg²⁺ ions bound is so strongly unfavorable as to be nearly impossible.⁴⁶ As shown in Figure 1B, the sequence of events in our proposed model of CDK2 catalysis at the roughly physiological condition we tested (pH 7.5, 162 mM ionic strength, 1 mM Mg²⁺_free, 3–5 mM ATP) are that ATP·Mg and protein substrates bind and then MgI binds, closing the Glycine-rich loop and promoting phosphoryl transfer (TS); next, the phosphorylated protein is released and the Glycine-rich loop opens, resulting in the ADP·2Mg state, MgI is released, followed by ADP·MgII release. Finally, after ADP·Mg release the apo kinase can bind ATP·Mg and protein substrate to start the catalytic cycle again.

Many different protein kinases are proposed to utilize two Mg²⁺ ions to catalyze the phosphoryl transfer reaction.^{11,13,14,44,47−50} This is supported by the strong conservation of the protein kinase active site residues coordinating the nucleotide phosphates (e.g., K33, DFG, and the catalytic HRD motif). It is likely that this model of the roles of equilibrium Mg²⁺ binding in phosphoryl transfer and ADP release is relevant to many different protein kinases where the 2Mg protein kinase reaction mechanism is conserved. Most kinases which utilize two Mg²⁺ ions to promote phosphoryl transfer by stabilizing the TS might be expected to demonstrate a similar inhibition of ADP release when both Mg²⁺ sites approach saturation at higher [Mg²⁺]_free. Despite this prediction, some kinases, like ERK2,¹⁴ are not reported to show CDK2-like inhibition of catalytic activity at higher [Mg²⁺]_free while still other kinases, like PKA,⁴⁷ are more sensitive to Mg²⁺ inhibition than CDK2. Because the affinity of the second Mg²⁺ is a function of both structural and electrostatic effects, explanations for these differences could come from sequence variation of less conserved residues, even distant from the active site, as well as other structural differences that could alter the relative affinity for Mg²⁺ binding to the MgI site. Kinases for which ADP release is fast are predicted to have weaker affinity for the second Mg²⁺ when nucleotide is bound, while kinases for which ADP release is slow are expected to have stronger affinity for the second Mg²⁺ when nucleotide is bound. Because ATP and ADP are so similar, it is difficult to alter the Mg²⁺ binding affinity to the ATP substrate MgI site without introducing similar effects to the ADP product MgI site.

For fully activated CDK2, evolution appears to have succeeded at optimizing the balance between favorable ATP activation and phosphoryl transfer benefits of utilizing two Mg²⁺ ions in the active site against the perhaps unavoidable efficiency limits introduced by 2Mg stabilization of the bound ADP product. The affinity of a protein kinase for the binding of the second Mg²⁺ at the MgI site may be largely determined by the strength of the electrostatic deficit in the active site generated by the close proximity of the phosphates and other charged active site residues. The strong effects that MgI recruitment clearly has on enzyme turnover may mean that dynamically altering the MgI affinity represents a tunable mechanism used for regulation of kinase catalytic activity. Recruitment of Mg²⁺ to the MgI site could be looked at as the protein kinase regulatory equivalent of insertion of an Arg finger by a G-protein activator protein (GAP)⁷ while destabilization of the ADP-bound MgI site may parallel the regulatory effect of a G-protein exchange factor (GEF), a key difference being that an activated protein kinase independently represents an optimal balance between the rates of these two potentially rate-determining steps.

Supporting Information Available

Measurement of ADP binding affinity by ITC, solvent viscosity effect experiments, derivation of solvent viscosity contributions to product release, substrate K_M, crystallography statistics, summary of MD simulations, and full citation for Gaussian03. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

The manuscript was written through contributions of all authors.

The authors declare no competing financial interest.