Variational Bayes Analysis of a Photon-Based Hidden Markov Model for Single-Molecule FRET Trajectories

Abstract

Single-molecule fluorescence resonance energy transfer (smFRET) measurement is a powerful technique for investigating dynamics of biomolecules, for which various efforts have been made to overcome significant stochastic noise. Time stamp (TS) measurement has been employed experimentally to enrich information within the signals, while data analyses such as the hidden Markov model (HMM) have been successfully applied to recover the trajectories of molecular state transitions from time-binned photon counting signals or images. In this article, we introduce the HMM for TS-FRET signals, employing the variational Bayes (VB) inference to solve the model, and demonstrate the application of VB-HMM-TS-FRET to simulated TS-FRET data. The same analysis using VB-HMM is conducted for other models and the previously reported change point detection scheme. The performance is compared to other analysis methods or data types and we show that our VB-HMM-TS-FRET analysis can achieve the best performance and results in the highest time resolution. Finally, an smFRET experiment was conducted to observe spontaneous branch migration of Holliday-junction DNA. VB-HMM-TS-FRET was successfully applied to reconstruct the state transition trajectory with the number of states consistent with the nucleotide sequence. The results suggest that a single migration process frequently involves rearrangement of multiple basepairs.

Introduction

Single-molecule fluorescence resonance energy transfer (smFRET) is a powerful technique for investigating conformational states of biomolecules without ensemble averaging. In addition to static distribution of conformational states (1–4), structural dynamics can be examined by statistical analysis (1,5–7) or by tracing fluorescence time series (7–9). Examination of the conformational dynamics of biomolecules is critical to understanding many of the mechanisms behind life, such as molecular motors (10,11), enzymatic reactions (12,13), and signal transduction (14,15). Furthermore, it is suggested that complicated processes at molecular level, such as the memory effect, play important roles in cellular activity (14,16–18).To observe such reactions and elucidate the mechanisms behind them, it is essential to measure dynamics experimentally by tracing conformational changes in real-time with single-molecule sensitivity. The time-resolved smFRET technique seems to be one of few choices currently capable of achieving this.

Fluorescence signal from a single molecule is so weak that stochastic fluctuation intrinsically involved in single photon signals—the so-called “shot noise”—is significant. Although time-averaging of the signal is commonly used to reduce such fluctuation, this degrades the time resolution as a trade-off and prevents us from tracing the molecular dynamics, which may have a timescale of milliseconds or faster. It is therefore desirable to improve the time resolution as well as the accuracy of smFRET measurements to allow observation of various biomolecular dynamics. One approach is to improve photon detection to enrich obtainable information. The common single-photon counting (SPC) measurement counts-up photons for individual time bins with fixed duration. However, binning discards details of the temporal distribution of photons and degrades information to some extent. Imaging by camera works the same way in principle, except that extra noise is added during electric amplification. To extract information as efficiently as possible, the time-stamp (TS) measurement has been introduced (7,12,19–21). Because the TS signal records the detection time of every single photon using SPC detectors, information about photon distribution is not degraded. Another important approach is through data analysis based on statistics or information theory. In particular, because TS signals are not intuitively understandable, data analysis is important to visualize its meaning. For example, schemes for extracting a smoothed FRET trajectory from a TS signal based on maximum-likelihood theory (22) or Fisher information (23) have been proposed.

Single-molecule signals often show stepwise changes in time series that are usually explained by proposing that the molecule consecutively repeats transitions between a finite number of states (NoS). As long as we assume such stepwise dynamics, the problem exists as to how to resolve states and detect transitions from signals. Early experimenters resolved states “by eye” but this cannot be very reliable. In addition, the NoS is usually unknown and must therefore also be guessed from experimental data. Various statistical analyses have been proposed to resolve the above problems. One approach is to find the change points, a data point that is placed at the boundary between states. Change point detection (CPD) for the TS signal using maximum likelihood estimation, followed by applying the Bayesian information criterion to decide the NoS, was proposed by Watkins and Yang (24) while Ensign and Pande (25) proposed CPD for SPC signals based on Bayesian inference. They both treated the intensity signal on a single detection channel, which is applicable to the donor-quenching type of FRET measurements. It has been shown that the hidden Markov model (HMM) approach can treat SPC-based FRET signals using maximum likelihood estimation and the Bayesian information criterion (26,27). The HMM was also applied to TS-intensity signals to analyze interconversion between two states (28) or multiple stepwise decay of clustered fluorophores (29). Another approach resolves transitions between two states from the TS-FRET signals by maximizing likelihood (30). Analysis of the local equilibrium state, proposed by Baba and Komatsuzaki (31), is a generic approach that may be suitable for smFRET systems, too.

In this article, we propose the use of variational Bayes (VB) inference to solve the HMM for TS-FRET signals. The advantage of VB is that it allows us to choose the optimum model from among various models, where, in the context of this article, difference of model means a difference in NoS. In 2009, Bronson et al. (32) proposed the VB-HMM approach to treat time-binned FRET signals by assuming a Gaussian distribution for the FRET efficiency. That approach, however, cannot make full use of the richer information that TS measurements can provide. It is not straightforward to apply the HMM to TS signals because time intervals between data points are not uniform, whereas the common HMM assumes uniform intervals. Here, we expanded the VB-HMM to treat TS-FRET signals (VB-HMM-TS-FRET). We also derived VB-HMM models for TS-intensity signals (VB-HMM-TS), SPC-based intensity (VB-HMM-PC), and FRET (VB-HMM-PC-FRET) signals, and used the TS-based intensity CPD (24) for comparison. By comparing results of these analyses, applied to several sets of data generated by Monte Carlo simulation, the accuracy and robustness of what to our knowledge is our new VB-HMM-TS-FRET model is demonstrated. Finally, we demonstrate the application of the developed analysis to experimental data. Time-stamped smFRET signals were acquired from spontaneous branch migration of single Holliday junction (HJ) DNA. VB-HMM-TS-FRET analysis was successfully applied and was able to reconstruct FRET trajectories corresponding to the state transitions.

Theory

Background

Photon emission from a fluorescent molecule is a stochastic process. Even if the average intensity appears to be constant, the temporal distribution of photons is uneven (Fig. 1 A). Using SPC detectors, such as photomultiplier tubes or avalanche photodiodes, which can detect individual photons, the absolute times, t_n, at which the n^th photon is detected can be recorded for all photons by TS measurement. When the experimental observable x_n for the n^th photon is defined as x_n ≡ Δt_n = t_n – t_n−1, it is known to obey the exponential distribution

$$p\left(x_n|I\right)=I\text{exp}\left(-I{x}_n\right),$$ (1)

where the intensity I is the average number of photons per second. Detected photons are often accumulated into time bins and plotted as a time series of intensity, which, in this article, we call the SPC signal (Fig. 1 B). In the SPC signal, the n^th data point x_n represents the photon count in a bin and obeys the Poisson distribution

$$p\left(x_n|\mu \right)=\frac{{\mu }^{x_n}}{x_n!}\text{exp}\left(-\mu \right),$$ (2)

where μ is the average count per bin.

Figure 1.

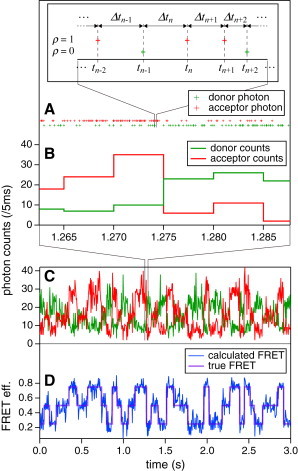
Example of TS-FRET signals, illustrating the relationship between TS and SPC signals. (A) The TS-FRET signal records arrival times of every single photon on the donor (green) and the acceptor (red) detector channels. (Inset) Experimental observables t, Δt, and ρ. (B and C) The SPC signals are made by binning photons with a fixed time period. (D) The time bin-based FRET trajectory (blue) is calculated from the SPC signals. The true FRET trajectory (purple) changes stepwise, showing the typical feature of single-molecule signals. (Color online.)

In two-color FRET experiments, spectrally separated photon counts are detected (Fig. 1 C) and the time series of the FRET efficiency, E, is calculated from these (Fig. 1 D). Such smFRET signals typically show a stepwise trajectory. This can be interpreted as that the sample molecule remaining in one of the possible states in a plateau region and instantaneous transition occurs. Under the assumption of such dynamics, we must divide the trajectory into short periods and assign each to an appropriate state (23,26,27,32). In the following, we briefly introduce what to our knowledge is a new scheme to treat TS signals by employing VB and the HMM. The details of the derivation can be found in the Supporting Material.

Variational Bayes to solve HMM

The HMM approach has been successfully applied to reproduce the state transition trajectories from stepwise FRET trajectories (26,27,32). Generally, provided the experimental data are given as a time series X = {x₁,…,x_N}, where N is the total number of data points, every single data point should be assigned to one of states. The latent variables, Z = z₁,…,z_N and z_n = {z_n1,…,z_nK}, are defined to represent the state transition trajectory so that z_nk is equal to 1 if the molecule belongs to the k^th state at the n^th time step, and 0 otherwise, where K is the assumed NoS. In the HMM, a simple Markov chain model is often assumed, i.e., which state the molecule resides in at the n^th time step depends only on the state at the (n−1)^th time step. The joint probability distribution over both the observables and the latent variables can then be written as

$$p\left(\mathbf{X},\mathbf{Z}|\Theta ,M\right)=p\left({\mathbf{z}}_1|\Theta ,M\right)\times \prod _{n=2}^{N}p\left({\mathbf{z}}_n|{\mathbf{z}}_{n-1},\Theta ,M\right)\times \prod _{m=1}^{N}p\left(x_m|{\mathbf{z}}_m,\Theta ,M\right),$$ (3)

where Θ and M represent a set of parameters and the model, respectively.

In 2009, the VB inference was introduced to solve the HMM for the FRET time series (32). VB evaluates the evidence, which is given by marginalizing parameters and the latent variable from the joint probability as

$$p\left(\mathbf{X}|M\right)=\sum _{\mathbf{Z}}\int d\Theta p(\Theta )p\left(\mathbf{X},\mathbf{Z}|\Theta ,M\right),$$ (4)

where p(Θ) is the prior probability distribution for Θ. After we obtain a set of data X, we must find the optimum set for the latent variable and the parameters to maximize this evidence. This can be achieved by following a procedure similar to the expectation-maximization-algorithm (26,27,33) (see details in Section S1.1 in the Supporting Material). The evidence can be compared among different models because it depends only on X and M. The VB treats and optimizes the probability distributions for parameters instead of their quantities and implicitly includes a penalty against decreasing Shannon’s entropy (32). Therefore, VB can find the optimum NoS without additional procedures, such as Akaike or Bayesian information criterion.

Formalism for the TS signals

In this article, we applied the VB-HMM to the TS signals (see details in Sections S1.2 and S1.3 in the Supporting Material). The common HMM assumes that the time interval between data points is uniform so that the probabilities of transition can be represented by the constant matrix A. However, because the time intervals vary in the TS signals, the transition probabilities between data points also change. Therefore, we use the transition rates k_i and the probabilities κ_ij(i ≠ j), which designate the destination of the transition, rather than the A-matrix. The value k_i must be sufficiently small compared with the photon emission rate, I_i, for the i^th state to be detected. The lower bound of photon sampling interval accessible by the TS measurement is typically ∼1 μs, which is limited by the response speed of detectors. The transition probability distribution should then be rewritten with dependence on x as

$$p\left(z_{nj}|z_{n-1,i},x_{n-1},\mathbf{k},\kappa ,\mathbf{I}\right)=\{\begin{array}{cc}\text{exp}\left(-k_i{x}_{n-1}\right)& \left(i=j\right)\\ {\kappa }_{ij}\left\{1-\text{exp}\left(-k_i{x}_{n-1}\right)\right\}& \left(i\ne j\right)\end{array}.$$ (5)

Further mathematical details are described in Section S1.2 in the Supporting Material.

The emission probability of the TS signal can be written as the exponential distribution (Eq. 1). To treat the TS signals of two-colored smFRET experiments, we introduce another variable to distinguish the detection channels,

$${\rho }_n=\{\begin{array}{cc}0& \left(\text{donor}\right)\\ 1& \left(\text{acceptor}\right),\end{array}$$ (6)

as depicted in the inset of Fig. 1. Now the observable is not a scalar but a vector, written as x_n = {Δt_n, ρ_n}. A new parameter E, which represents the FRET efficiency, is also introduced. The emission probability for TS-FRET signals can be factorized and becomes

$$p\left({\mathbf{x}}_n|I,E\right)=p\left({\rho }_n|E\right)\times p\left(\Delta t_n|I\right),$$ (7)

$$=E^{{\rho }_n}{\left(1-E\right)}^{1-{\rho }_n}\times I\text{exp}\left(-I\Delta t_n\right).$$ (8)

Formalism for the SPC signals

To compare the TS-based analysis with the SPC-based analysis, we also formulate the VB-HMM for the SPC signals (see details in the Sections S1.4 and S1.5 in the Supporting Material). As described in Eq. 2, the observable x_n in the SPC measurements is the number of detected photons within a bin and the emission probability distribution is the Poisson distribution. For SPC signals, we employed the A-matrix for transition probabilities.

SPC-FRET signals are composed of two channels of SPC detection. The observable may be x_n = {d_n, a_n}, where d_n and a_n are photon counts on the donor and the acceptor channels, respectively, and both have a Poisson distribution. The likelihood function then becomes

$$p\left({\mathbf{x}}_n|\mu ,E\right)=p\left(d_n|\mu ,E\right)\times p\left(a_n|\mu ,E\right),$$ (9)

$$=\frac{{\left(1-E\right)}^{d_n}{E}^{a_n}}{d_n!a_n!}\times {\mu }^{d_n+a_n}\text{exp}\left(-\mu \right).$$ (10)

Numerical Experiments

To evaluate our analysis methods, we generated a fluorescence signal time series by simulating a molecule repeating transition among states. The model we used included three states, each of which was characterized by the average intensity, I_i, or the FRET efficiency, E_i. Photons are emitted at a constant rate but are stochastically distributed. The average lifetimes of states are defined by λ_i. Total signal length T is fixed at 10 s. Several analysis methods were applied to determine the likeliest NoS, to estimate the parameters and to reproduce the state transition trajectory.

In summary, we performed two sets of simulations:

First, we generated the intensity signal on a single detector channel, simulating the single-color FRET measurements, which detect the decrease in donor fluorescence. The intensity ratio is defined by a parameter I_ratio ≡ I₂/I₃ = I₁/I₂, which regulates the discrimination between states. The purpose of this simulation was to compare the performance and the efficiency of our VB-HMM-TS method with other photon-based analyses. We employed the CPD method as an alternative, which is the only other TS-based analysis method previously reported to our knowledge (24). We also used our VB-HMM-PC method with a few bin sizes to explore the difference between the TS and the SPC measurements.

Second, we assumed two-color FRET measurements and simulated dual-channel fluorescence signals. In this case, states were not characterized by the intensities but the FRET efficiencies, which are defined as E₁ = 0.5 − ΔE, E₂ = 0.5, and E₃ = 0.5 + ΔE with a parameter ΔE. Because there are, unfortunately, no previously proposed methods capable of treating the TS-FRET signals, we used only VB-HMM-FRET methods. In addition, we applied VB-HMM-TS/PC analyses to the donor signal extracted from the dual-channel signal. Conceptually, TS/PC-FRET analyses appear to be superior to TS/PC analyses because the number of photons dedicated to the analysis is larger, roughly double, in the FRET signals. However, firm conclusions may not be straightforward, because the quantity being evaluated is qualitatively different, i.e., intensity analysis detects changes in the photon density whereas the FRET analysis detects changes in the ratio of photon numbers between channels.

Details of definitions and procedures are described in Section S2.1 in the Supporting Material.

Results

Examples of analyses

Fig. 2 shows an example simulation and analysis set for the case of a single-channel intensity signal. With I_ratio = 0.5, the simulated states had intensities I = 2500, 5000, and 10,000 and lifetimes λ = 20, 10, and 5 ms, respectively. In Fig. 2 A, the simulated time series is represented in SPC-style with a bin size of 1 ms (dashed), 5 ms (solid), and 10 ms (gray) (the full-length data are shown in Fig. S1 A in the Supporting Material). Red crosses represent individual photons and indicate that information on the temporal distribution of photons is available. This time series was analyzed by VB-HMM-TS, CPD, and VB-HMM-PC with three bin sizes. Each analysis examined the likelihood of from 2- to 6-state models and decided the likeliest NoS. For this example data, the NoS was correctly assigned as three by all analysis methods (the resulting inference scores are shown in Fig. S2). Fig. 2 B shows the state transition trajectories (the full-length data are shown in Fig. S1 B). The correct answer, which is the simulated data, is plotted by red crosses. Blue and green crosses are assignments by TS-based analyses, VB-HMM-TS and CPD, respectively. VB-HMM-PC results are represented by gray (1 ms bin), dashed (5 ms bin), and light gray (10 ms bin) lines, respectively. One can see that all analysis methods reproduced the simulated trajectory quite well. The photon-based accuracy for reproducing the trajectory with this data was the highest with the VB-HMM-TS method at ∼90%. Reasons for the principal errors include time lags for state transitions and missing short-lived states. For example, CPD did not detect the short-lived peak at ∼4.7 s and both VB-HMM-TS and CPD resulted in a slight delay on the rising edge immediately after 4.68 s. SPC-based analyses reproduced the trajectories well with a small bin of 1 ms, whereas higher errors result with larger bins of 5 or 10 ms. Once the NoS is correctly inferred, the accuracy of parameter estimation seems reasonable, as discussed later.

Figure 2.

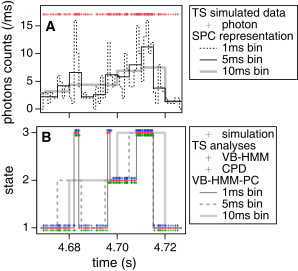
Example results of analyses of an intensity signal. (A) The SPC-signal with 1-ms (dashed), 5-ms (black), and 10-ms (gray) time bins are converted from a simulated TS signal (red). (B) The state transition trajectories. The original simulated data (red), the results of VB-HMM-TS (blue), and CPD (green) assign a state to each photon. The VB-HMM-PC results with 1-ms (gray), 5-ms (dashed), and 10-ms (light-shaded) bins are time-bin-based. I_ratio = 0.5 and {λ₁, λ₂, λ₃} = {20, 10, 5} ms were applied for this simulation. Full-length data are shown in Fig. S1 in the Supporting Material.

An example of two-color TS-FRET simulation and analytical results is shown in Fig. 3. With ΔE = 0.1, the same intensity I = 10,000 and lifetime λ = 100 ms were given to all states. In Fig. 3 A, green and red lines show the SPC representation of donor- and acceptor-signals of simulated data with a 5-ms bin, respectively. The blue lines above these are the FRET efficiencies E = I_A/(I_A + I_D) calculated for each bin, where I_A and I_D are the donor and the acceptor intensities, respectively. Trajectories using 1-ms bins are plotted together as light-colored lines (the full-length data are shown in Fig. S3 A). All the TS- and the SPC-based analyses gave the highest score at the NoS of three, which is the correct answer (the variational lower bounds are shown in Fig. S4). Fig. 3 B shows the state trajectory of Fig. 3 A from simulation and analytical results (the full-length data are shown in Fig. S3 B). Red dots represent the simulation-data photon by photon. Assignments by TS-based analyses are plotted by blue (TS-FRET) and light-blue (TS) dots, respectively. For SPC-based analyses, the results for 1-ms bins were plotted by dotted gray (PC-FRET) and solid light gray (PC) lines. The accuracy of the inference of photon-based state trajectory was higher when using TS-/PC-FRET models (>90%) than TS/PC models (∼82–85%). It can be seen in Fig. 3 D that the FRET analyses can trace the transient stay of state 2 just before 7 s, but the intensity analyses missed this state. Once the NoS is guessed correctly, the accuracy of the parameter estimation appears to be quite good, as shown below.

Figure 3.

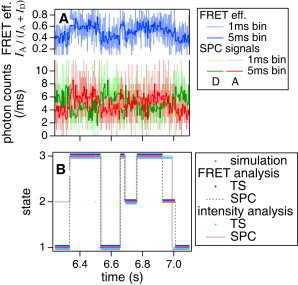
Example results of analyses of a dual-channel FRET signal. (A) The SPC-signals with 5-ms time bins (donor, green; acceptor, red) are converted from the simulated TS signal (not shown). The FRET trajectory (blue) is calculated from the SPC trajectories. Light-colored lines are plots using 1-ms time bins. (B) The state transition trajectories. The original simulated data (red), the results of VB-HMM-TS-FRET (blue), and VB-HMM-TS (light blue) assign a state to each photon. The results of VB-HMM-PC-FRET (dashed gray) and VB-HMM-PC (light gray) only with 1-ms bin are shown. VB-HMM-TS/-PC analyses treat only the donor photons. ΔE = 0.1, I = 10,000, and λ = 100 ms were applied to all states. Full-length data are shown in Fig. S3.

Statistics of one-channel TS intensity signals

In Fig. S5, we summarize the performance of analytical methods evaluated from 1000 iterations of simulation-analysis cycles. Some representative results for six sets of λ with I_ratio = 0.5 are shown in Fig. 4. Because the representations in Fig. 4, panels A and B, were not created from states but from the whole signals, their horizontal axes are represented by the value λ₃.

Figure 4.

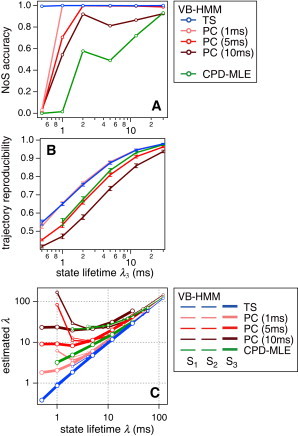
Statistics of an intensity analysis on 1000 Monte Carlo-simulated time series data with I_ratio = 0.5. (A) The accuracy of the NoS estimation. VB-HMM-TS achieves almost 100% accuracy over this parameter range, while VB-HMM-PC with 1-ms bin is close. (B) The accuracy in reproducing the state transition trajectory. VB-HMM-TS and VB-HMM-PC (1 ms) are again superior to others. CPD, another TS-based analysis, is equivalent at large λ. (C) The accuracy of parameter estimation of the transition rates given by the state lifetime λ. VB-HMM-TS shows almost perfect results. Error bars designate the standard deviation. Further results are summarized in Fig. S5.

Fig. 4 A shows the accuracy, which is defined as the probability that the number of states was correctly guessed as three. VB-HMM-TS maintained nearly 100% accuracy over the whole range of λ, even down to a few milliseconds. VB-HMM-PC, with the smallest bin, was similar but dropped at very small λ. VB-HMM-PC caused more errors with larger bin sizes, as one may expect. CPD seems to be erroneous and even worse than VB-HMM-PC with large bin sizes, whereas it makes use of richer information in the TS signal than that of the SPC signal.

Fig. 4 B shows the reproducibilities of the state transition trajectory. The fraction of photons assigned the correct state was calculated only from the trajectories for which the NoS were correctly guessed as three, and the average is plotted with error bars designating the standard deviation. Among the methods, the best results were given by VB-HMM-TS and VB-HMM-PC with a 1-ms bin. To achieve 90% reproducibility, which corresponds to the result shown in Fig. 2, several tens of photons per state are needed when I_ratio = 0.5. CPD follows these and was almost equivalent when λ was large enough. The reproducibility of VB-HMM-PC was degraded with larger bins, as may be expected.

Generally, although the accuracy of the NoS guess and/or the trajectory reproducibility is good, the accuracy of the parameter estimation also appears to be fairly reliable. Fig. 4 C shows the accuracy of estimation for the parameters λ. Surprisingly, VB-HMM-TS gives almost perfect results once the NoS is correctly guessed.

Statistics for two-channel time-stamped FRET signals

The statistics of VB-HMM analyses of two-channel TS-FRET simulation are summarized in Fig. S6. Some representative results with ΔE = 0.1 are shown in Fig. 5.

Figure 5.

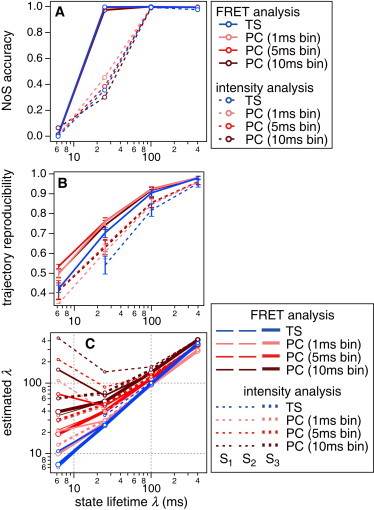
Evaluation of the FRET signal analysis on 1000 Monte Carlo-simulated time series data with ΔE = 0.1. (Solid lines) Results of the FRET analyses. (Dashed lines) Intensity analyses. (A) The accuracy of the NoS estimation. (B) The reproducibility of the state transition trajectory. (C) Estimation of the transition rates, given by the state lifetime λ. VB-HMM-TS-FRET again shows almost perfect results. Overall, the FRET analyses are superior to the intensity-based analyses. Error bars designate the standard deviation. Further results are summarized in Fig. S6.

Fig. 5 A shows the accuracy of the NoS guess. Overall, dual-FRET analyses (solid lines) are superior to single-channel intensity analysis (dashed lines). This indicates that, although the quantity used to evaluate statistics is qualitatively different as mentioned above, VB-HMM analyses make use of the richer information of the two-color FRET signals. Among FRET analyses showing similarly good performance, TS-FRET and PC-FRET with 1-ms bin seem to be superior at small λ with ΔE = 0.2 (see Fig. S6 A). To achieve >90% accuracy of the NoS guess with ΔE = 0.1, several hundreds of photons per state is required, whereas a few tens of photons are sufficient when ΔE ≥ 0.2 can be expected.

Fig. 5 B shows the reproducibility of the state transition trajectory. Again, overall, dual-channel FRET analyses gave better results than single-channel intensity analyses. For this set of analyses, PC-FRET with a 1-ms bin appears to be the best, while TS-FRET is similar.

During estimation of parameters, the accuracies seem to depend on the NoS accuracy and the results appear to be good, except at small λ (see Fig. S6, E–J). For estimation of the state lifetime, λ, TS-FRET analysis was again almost perfect in all cases (Fig. 5 C and Fig. S4, I and J). PC-FRET with a 1-ms bin was almost equivalent except that an error can be seen at small λ.

smFRET measurement of spontaneous branch migration of Holliday junction

Holliday junction (HJ) is a four-way junction structure of DNA, which is comprised of four DNA strands and arises in homologous and site-specific genetic recombination (34–36) or DNA repair (37). Movement of the crossover junction along DNA is termed “branch migration” (Fig. 6 A) and is a key mechanism in genetic processes. Although branch migration is thought to be driven by the protein complex RuvAB in vivo (38,39), it can also take place spontaneously because branch migration of homologous DNAs is an isoenergetic process, which does not alter the number of hydrogen bonds. Spontaneous branch migration has been observed in vitro by biochemical (40) and single-molecule experiments (41,42).

Figure 6.

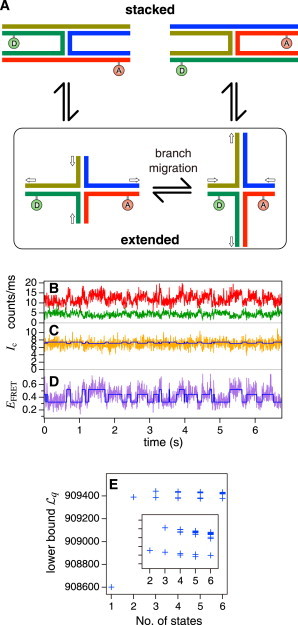
(A) Schematic of branch migration of the Holliday junction. “D” (donor) and “A” (acceptor) represent fluorescent labels. (B) Time series of fluorescence intensities from the donor (green) and the acceptor (red), respectively, acquired by smFRET observation of spontaneous branch migration. (C) Compensated intensity I_C (yellow) and (D) FRET efficiency E_FRET (purple) calculated from fluorescence intensities. (E) Variational lower bounds given by VB-HMM-TS-FRET analysis. The maximum lower bounds were obtained with the NoS of three. I_C and E_FRET trajectories reconstructed from the VB-HMM-TS-FRET result are overlaid (blue) in panels C and D, respectively. (Color online.)

The molecular mechanism of spontaneous branch migration is not fully understood yet. However, a persuasive model has been suggested: two HJ conformations exist in equilibrium, namely, stacked and extended (43). HJ is stabilized in the stacked conformation in the presence of multivalent cations such as Mg²⁺. However, once HJ occasionally switches to the extended conformation, it can migrate by rearrangement of basepairs around the crossover point until it switches back to the stacked conformation (40). Because basepair rearrangement is a stochastic process, branch migration is a one-dimensional random-walk process. It had been suggested that the base rearrangement takes place with single bases (40), but hops over multiple basepairs were recently observed (42). To investigate the details of HJ conformational dynamics, both single-molecule observations in real-time and exact analysis of those data are necessary.

We prepared double-fluorescence-labeled HJs and conducted smFRET measurement of spontaneous branch migration. HJs were immobilized on a coverslip surface by avidin-biotin coupling and observed by a confocal microscope system. Our HJ was designed so that the branch could migrate between three different positions. See details in Subsections S2.2–2.3 in the Supporting Material.

PC representations of example fluorescence signals from a single HJ are shown in Fig. 6 B while raw data were acquired by TS measurement. Green and red lines are fluorescence signals of the donor and the acceptor, respectively, with a 5-ms time bin. The compensated intensity I_C, which is defined by Eq. S60 in the Supporting Material, is plotted as a yellow line in Fig. 6 C. Because I_C is constant except for fluctuations caused by shot noise, we can say that variations in the fluorescence signals are caused by FRET changes, not by photochemical effects such as blinking. The FRET trajectory was also calculated using Eq. S59 in the Supporting Material and plotted as a purple line in Fig. 6 D. Stepwise changes in the FRET trajectory can be seen.

VB-HMM-TS-FRET analysis was applied to these data. The resulting variational lower bounds are plotted in Fig. 6 E. The maximum lower bounds were obtained when NoS was three, which corresponds to that expected from our HJ according to its sequence. I_C and E_FRET trajectories were reconstructed from the VB-HMM-TS-FRET result, which gave the maximum lower bound, and are overlaid on Fig. 6, C and D, as blue lines. The reconstructed I_C is almost constant, again, and E_FRET exhibits stepwise changes.

We collected nine similar experimental data sets, including that of Fig. 6, and analyzed these by VB-HMM-TS-FRET in the same manner. All data and analysis results are shown in Fig. S12. Some were assigned more than three states, some of which were transient dark states and obviously seem likely to be caused by blinking. Apart from such blinking states, the reproduced trajectory of the FRET efficiency showed transitions among the three states. Estimated parameters for the three major states are summarized in Table S1 in the Supporting Material. Histograms of the FRET efficiency made from E_FRET trajectories with a 5-ms bin (green) and stepwise trajectories reproduced by analysis (blue), respectively, are shown in Fig. 7. Whereas the green histogram shows one broad distribution, from which it is hard to resolve states, the blue histogram shows three distinct peaks.

Figure 7.

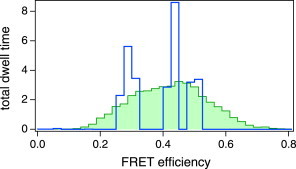
Histograms of the FRET efficiency created from nine sets of smFRET time series. (Green histogram) Constructed from the FRET trajectories with a 5-ms bin, calculated directly from the fluorescence signals, forms a single broad peak. Individual states are not distinguishable. (Blue histogram) Constructed from the VB-HMM-TS-FRET results, in which three distinct distributions are clearly shown. (Color online.)

Discussion

We have shown that VB-HMM analyses have the ability to guess the NoS, reproduce the state transition trajectory, and estimate parameters with great accuracy.

We expected that the ultimate time resolution of single-molecule measurements could be achieved by photon-by-photon detection and analysis. The time resolution may be defined with the average number of photons detected during a single stay of the state, because information in the TS signals is governed by the temporal photon distribution and is independent of the absolute time. Here, we focus on the minimum photon number required to achieve 90% trajectory reproducibility, at which almost 100% NoS accuracy is achieved. For single-channel intensity signals, ∼100 photons are required with an intensity ratio I_ratio of 0.5 between adjacent states. When I_ratio of 0.25 is expected, a few tens of photons are sufficient. This is smaller than the previously reported CPD, which required a few hundred photons per state to resolve two states with I_ratio of 0.5 (24). For dual-channel FRET signals, ∼1000 photons are required to resolve $\Delta E$ = 0.1 and a few hundreds of photons are sufficient if ΔE ≥ 0.2.

The results shown in Fig. 5 and Fig. S6 suggest that it is desirable to perform FRET dynamics measurements with a double fluorescently labeled target and simultaneous two-color TS detection.

Together with TS-based analyses, for the first time to our knowledge we also derived Poisson-based VB-HMM-PC methods, the performance of which crucially depends on bin size. When bins are too large, the quality of analysis is degraded, as shown in Figs. 4 and 5 (see also Fig. S5 and Fig. S6). We found that the errors in estimation of the NoS were often overfitting. Artifactual intermediate states, which arose when the state transitions occurred in the middle of a time bin (32), might cause those over-fit errors. Because a longer time bin is more likely to include a transition, the bin size must be set short enough to avoid such artifactual overfitting. To see how small bins should be, Figs. 4 C and 5 C (see also Fig. S5, G–H, and Fig. S6, I–J) are replotted in Fig. S7 so that the state lifetime λ is normalized as the ratio to the bin size. It indicates that the accuracy of analysis depends on the ratio rather than on the bin size itself and the bin size must be smaller than, for example, half of λ. If time resolution of PC detection or the camera’s frame rate is insufficient to it, one may have to seriously consider switching to the TS measurement.

Our results show that VB-HMM-PC performs equivalently to VB-HMM-TS methods or even slightly better for FRET analysis, as long as the bin size is appropriately defined. One may prefer to use an SPC-based analysis because of this advantage. However, even so, it is still desirable to acquire the TS signal, because it is difficult to decide the optimum bin size in advance of conducting experiments and a measurement with an inappropriate bin size will affect the analytical result, as discussed above. After the TS data are obtained, the SPC data can be easily constructed with an arbitrary bin size and, furthermore, the use of TS-based analysis frees one from worrying about binning.

Some research groups have reported the application of the HMM to analyze smFRET signals (26,27,32). They also evaluated their analytical schemes using simulated data sets and showed good performance. They treated SPC-based FRET trajectories and gave quite large parameters ΔE ≥ ∼0.2 or even ∼0.4, and small dispersion, down to ∼0.02. The required number of photons per bin to keep dispersion under 0.1 or 0.02 at E = 0.5, was ∼24 or >600, respectively (44). In addition, they simulated the photon counts or the FRET value for every bin, which can avoid the generation of artifactual intermediate states mentioned above, whereas the TS signals were converted into SPC signals in our simulation. Finally, they successfully analyzed trajectories composed of states having lifetimes of at least tens of bins, which includes thousands of photons. In summary, our VB-HMM-TS/PC-FRET methods have accuracy and time resolution at least comparable to theirs.

We considered two other factors that may affect the quality of the analyses. The first was the total signal length T, which was fixed to 10 s in the simulations described above. Because the number of observed transitions is determined by T, analyses may lack reliability with shorter T. To verify dependence on T, we conducted another set of simulations, as described in Section S2.1.2 in the Supporting Material. The results indicate, as shown in Fig. S8 and Fig. S9, that the trajectory must be long enough so that every state appears at least seven times in average under our simulation conditions. The second factor considered was noise. Photon-counting signals generally contain intrinsic dark counts and background counts, both of which are indistinguishable from the signal photon counts and cause difficulty in resolving states by lowering signal contrast. A detailed discussion on noise is provided in the Section S2.1.3 in the Supporting Material. The results of another set of simulations, shown in Fig. S10 and Fig. S11, indicate that analysis was barely affected at the noise levels in our experimental condition, which was typically <5% of signals.

The VB-HMM analyses developed were applied to experimental data obtained from smFRET measurement of spontaneous branch migration of HJ DNA. VB-HMM-TS-FRET was successfully applied and NoS estimated to be three, which was consistent with the NoS that the HJ sequence is designed to exhibit, except for the obvious blinking states detected in some cases. Transitions between the states can be examined in detail from the reproduced FRET trajectories. Transitions between states 1 and 3, which correspond to a 2-bp migration hop, can be seen as often as transitions to state 2, which may be a 1-bp migration, whereas transitions from state 2 are always expected to be a 1-bp hop. This means that a 2-bp hop can occur frequently, as indicated in a previous report (42).

Conclusion

We have shown that VB-HMM-TS-FRET is a robust and accurate method to analyze smFRET trajectories, as long as a sufficient number of signal photons are supplied. Our results clearly suggest that dual-channel detection is preferable for smFRET experiments to the donor-only detection configuration. We compared TS- and SPC-based analyses and VB-HMM-PC-FRET also showed good performance when the bin size was appropriate. However, we conclude that VB-HMM-TS-FRET is preferable because of the following three points:

• 1.There is no necessity to decide the size of time bins.
• 2.The quality of analysis is equivalent to the best results of VB-HMM-PC-FRET under optimal conditions.
• 3.Estimation of the parameter λ is almost perfectly accurate.

The time resolution of TS-based analysis actually depends on the photon rate. The fluorescence emission rates of common dyes are still far from the limitation of SPC detectors, whereas the frame rate may comprise another bottleneck in camera imaging. If photon emission rates are improved, for example by engineering brighter fluorophores or suppressing photochemical reactions (45), the time resolution automatically improves.

One of the advantages of the VB-HMM approach is flexibility. That is, by applying a generic derivation procedure, it is relatively easy to change or expand the model in question. For example, introduction of simultaneous multiparameter measurements, such as fluorescence spectrum, fluorescence lifetime, polarization, and so on, into single-molecule experiments has been proposed (10,46–48). If the enriched information does not affect the transition probability distribution, we simply have to modify the emission probability distribution to a multivariate. For example, we added a term of likelihood for photon color to that on the time interval (see Eq. S39 in the Supporting Material) or photon counts (see Eq. S53 in the Supporting Material) to treat FRET information. Statistics that are based on enriched information will improve the accuracy of inferences and finally the time resolution of measurements.