Skip to main content
PMC home page
Biomedical Optics Express logoLink to Biomedical Optics Express
. 2012 Aug 14;3(9):2121–2130. doi: 10.1364/BOE.3.002121

The influence of frontal sinus in brain activation measurements by near-infrared spectroscopy analyzed by realistic head models

Kazuki Kurihara 1,*, Hiroshi Kawaguchi 2, Takayuki Obata 2, Hiroshi Ito 2, Kaoru Sakatani 3, Eiji Okada 1
PMCID: PMC3447554  PMID: 23024906

Abstract

Adequate modeling of light propagation in the head is important to predict the sensitivity of NIRS signal and the spatial sensitivity profile of source-detector pairs. The 3D realistic head models of which the geometry is based upon the anatomical images acquired by magnetic resonance imaging and x-ray computed tomography are constructed to investigate the influence of the frontal sinus on the NIRS signal and spatial sensitivity. Light propagation in the head is strongly affected by the presence of the frontal sinus. The light tends to propagate around the frontal sinus. The influence of the frontal sinus on the sensitivity of the NIRS signal to the brain activation is not consistent and depends on the depth of the frontal sinus, the optical properties of the superficial tissues and the relative position between the source-detector pair and the frontal sinus. The frontal sinus located in the shallow region of the skull tends to reduce the sensitivity of the NIRS signal while the deep frontal sinus can increase the sensitivity of the NIRS signal.

OCIS codes: (170.3660) Light propagation in tissues, (170.5280) Photon migration, (170.2655) Functional monitoring and imaging

1. Introduction

Near-infrared spectroscopy (NIRS) and optical imaging have been used to non-invasively measure cerebral oxygenation and hemodynamic changes associated with brain activation [1,2]. They have been widely applied to a variety of brain function studies [3–7] and clinical measurements [8–13]. In NIRS measurements, the source and detector probes are attached to the scalp to detect the change in optical density caused by the hemodynamic change in the brain. Consequently, the light needs to pass through the superficial tissues such as, scalp, skull both before and after passing through the brain tissue. It is important to obtain the sensitivity of the NIRS signal to the absorption change in the brain and the volume of tissue sampled with a particular source-detector pair, however, light is strongly scattered by the tissues, thus the path of light propagation in the head is ambiguous. Since light intensity in the head cannot be non-invasively measured by experiments, light propagation in the head has been predicted by simulations.

Light propagation in the head is affected by the heterogeneity in optical properties of the tissues. Especially, cerebrospinal fluid (CSF) that has both low scattering and absorption coefficients has a strong effect on light propagation in the brain [14–16]. The influence of a CSF layer cannot be ignored in any modeling of light propagation in the head. The boundaries between various tissues in the head have complex geometry. The brain surface is folded with sulci filled with the CSF. The geometry of the tissue boundaries is also important for adequate modeling of light propagation in the head. Recently, the realistic head models, the structures of which are based upon magnetic resonance (MR) head images has been used to predict light propagation in the head for NIRS and optical imaging [17–20]. These head models basically consisted of five types of tissues that imitate the scalp, skull, CSF, gray matter and white matter. A more sophisticated model, for instance, which includes the extra-cerebral vasculature, has been constructed to investigate the influence of the large pial vessels, such as sagittal sinus, on the diffuse optical imaging [21].

The frontal sinus (FS) in the skull is an optically void region. The analysis of light propagation in a simplified head model with a void region mimicking the FS indicated that light propagation in the brain is affected by the FS [22]. However, the FS tends to be ignored in the realistic head models based on the MR images because there is very little contrast between the FS and skull regions in the MR image to obtain precise geometry of the FS.

In this study, the 3D realistic head model including a FS is constructed in order to investigate the influence of a FS on the NIRS measurements. The FS can be clearly observed in images acquired by x-ray computed tomography (CT). The anatomical geometry of the head model is based upon MR and x-ray CT images. Three additional models including the artificially modified FS are also constructed and light propagation in these head models is compared to discuss the influence of the FS on the NIRS signal and the spatial sensitivity profile.

2. Method of simulation

2.1. Construction of the realistic head models

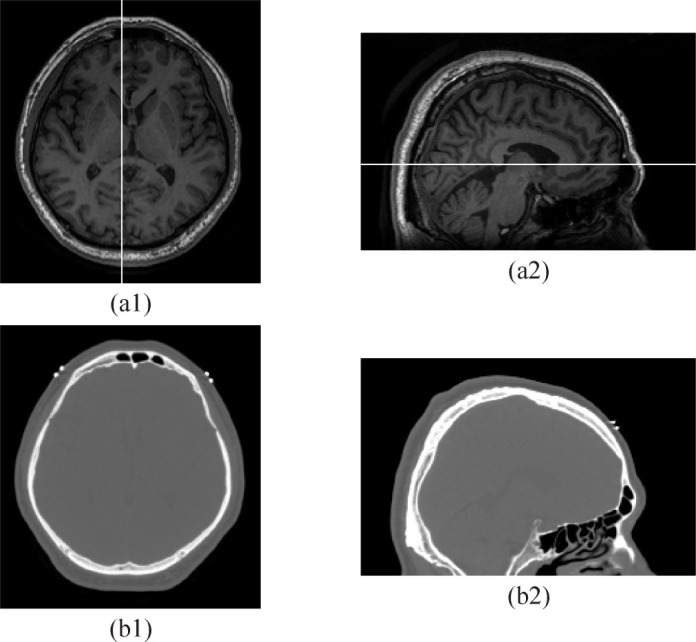
The geometry of the realistic head models is based on the anatomical images obtained by MR imaging and x-ray CT. The original 3D MR images contain 166 planes with 1.0 mm intervals and each plane consists of 256 × 256 pixels with square sides of 1.0 mm. The original 3D CT images contain 381 planes with 0.5 mm intervals and each plane consists of 512 × 512 pixels with square sides of 0.41 mm. Figures 1(a) and 1(b) show the T1-weighted MR image and CT image in the same plane of a slice, respectively. In the T1-weighted MR images, the contrast among the grey matter, white matter and CSF is sufficient enough to identify these boundaries. It is difficult to find the boundaries between the skull and the adjacent regions because bone and water (CSF) produce a low signal while the bone marrow and fat in the scalp produce a high signal. Since the air produces a low signal in the T1-weighted MR images, the region of the FS cannot be recognized in the images. In the CT images, the boundaries between the skull and adjacent regions are easily distinguishable and the FS is clearly observed in the frontal bone.

Fig. 1.

Fig. 1

Open in a new tab

(a1) An axial slice of MR image. (a2) A sagittal slice of MR image. (b1) An axial slice of CT image. (b2) A sagittal slice of CT image. The MR and CT images are in the same plane. White lines in (a1) and (a2) indicate the plane of the sagittal and axial slices, respectively.

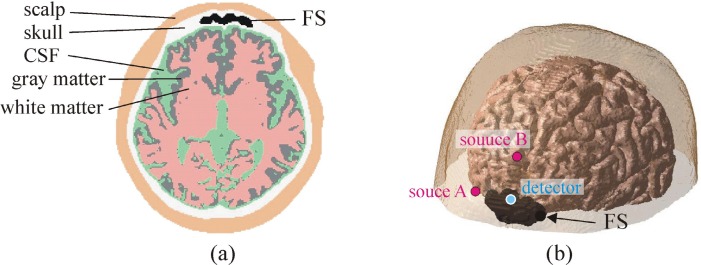
The head models consist of 6 regions, which include the air, scalp, skull, CSF (subarachnoid space), gray matter and white matter. Since the spatial resolution of the MR and CT images are different, the CT images were realigned by SPM8 software [23] to coregistrate images of the MR and CT. The MR and CT images were binarized by the conventional region growing algorithm [24] for the 3D grayscale images. The outer surface of the whole head, gray matter and white matter were identified from the MR images while the skull and air in the FS were identified from the CT images to determine the boundaries of each type of tissues. An axial slice of the head model segmented from the MR and CT images and the 3D segmented geometry of the head model are shown in Figs. 2(a) and 2(b), respectively. The outer surfaces of the whole head, FS and brain are represented in the 3D segmented geometry. The head models consist of 256 × 256 × 106 cubic voxels with side 1 mm. Each voxel is specified with its optical properties according to the results of the tissue segmentation. The optical properties of each type of tissues in the head models at the 830 nm wavelength were chosen from the reported data [16,25–27] (parameter set (I)). Actually, a wide range of different values in the optical properties has been reported for the same types of tissues. Light propagation in the head models with two additional parameter sets was predicted in order to investigate the dependence of the influence of the FS on the optical properties of the head. Extreme values were chosen based on the literature [21,28,29] as parameter set (II). The scattering coefficient of all the types of tissues in parameter set (II) is lower than those in parameter set (I). In parameter set (III), the optical properties of the scalp and skull are the same as those in parameter set (II) while the optical properties of the other parts of the head are the same as those in parameter set (I). The optical properties of each type of tissues in the head models are listed in Table 1 .

Fig. 2.

Fig. 2

Open in a new tab

(a) An axial slice of the segmented image of the realistic head model. (b) 3D segmented geometry of the realistic head model. The outer surfaces of the whole head, FS and brain are only represented.

Table 1. Optical properties of each type of tissues in the head model.

Parameter set Scalp Skull FS CSF Gray matter White matter
Transport scattering coefficient (mm−1) I 1.84 1.48 0.01 0.24 2.12 8.82
II 0.66 0.86 0.01 0.01 0.7 0.7
III 0.66 0.86 0.01 0.24 2.12 8.82
Absorption coefficient (mm−1) I 0.025 0.025 0.001 0.004 0.039 0.017
II 0.019 0.014 0.001 0.003 0.020 0.080
III 0.019 0.014 0.001 0.004 0.039 0.017
Open in a new tab

2.2. Modification of the FS

Three additional models were constructed to investigate the influence of the FS on the sensitivity of the NIRS signal. In the additional models, the geometry of the FS was only modified from that in the realistic head model shown in Fig. 2 (the model with the whole FS). Figure 3(a) shows an axial slice of the frontal area of the model with the whole FS. In the model without the FS, the FS is replaced by the skull as shown in Fig. 3(b). In the model with the shallow FS, half of the volume in the deeper region of the FS was replaced by the skull and that in the shallow region was replaced by the skull in the model with the deep FS as shown in Figs. 3(c) and 3(d), respectively.

Fig. 3.

Fig. 3

Open in a new tab

An axial slice of the head models for evaluation of the influence of the FS on light propagation in the head. (a) The model with the whole FS, (b) the model without the FS, (c) the model with the shallow FS, (d) the model with the deep FS.

2.3. Analysis of light propagation in the head models

Light propagation in the head models was calculated by use of a Monte Carlo method [30–32]. Refractive index mismatch was considered only at the interface between the scalp and air. The refractive indices of air and tissue were 1.0 and 1.4, respectively. A fraction of the photon weight absorbed at each interaction site was accumulated in each voxel in time-gates of width 50 ps to calculate the time-resolved photon fluence. When a photon packet reached the detector position, its ultimate weight was accumulated to calculate the detected intensity. The path length of the detected photon packet in each voxel and each type of tissues weighted by the ultimate weight was accumulated to calculate the spatial sensitivity profile and partial optical path length in each type of tissues. The partial optical path length can be used as an index of the sensitivity of the NIRS signal to global absorption change in a particular type of tissues while the spatial sensitivity profile indicates the volume of tissue sampled by the source-detector pair of the NIRS instrument. The positions of the sources and detector are shown in Fig. 2(b). The distance between each source-detector pair is 30 mm.

3. Results

3.1. Influence of the FS on light propagation in the head models

The time-resolved photon fluence maps in the head models with the whole FS and without the FS shown in Figs. 3(a) and 3(b), respectively, were predicted in order to evaluate the influence of the FS on light propagation in the head. A pulse of light was irradiated at source position A in Fig. 2(b) and the photon fluence maps during every 50 ps were recorded up to 2.5 ns. A frame from a movie (Media 1 (1.3MB, AVI) ) of the time resolved photon fluence map in the head models with parameter set (I) is shown in Fig. 4 . When the photon fluence reaches the FS at about 250 ps, the photon fluence around the FS rapidly increases. This causes the distortion of the photon fluence map and the distribution of the photon fluence is broadened in the direction of the FS. The penetration of the photon fluence tends to be confined to the gray matter and the photon fluence laterally spreads in the gray matter in both models. This phenomenon is caused by the low-scattering and low-absorption characteristics of the CSF.

Fig. 4.

Fig. 4

Open in a new tab

Frame from a movie (Media 1 (1.3MB, AVI) ) of light propagation in the head model with the whole FS and without the FS. The red region indicates the FS.

3.2. Influence of the FS on the NIRS signal and spatial sensitivity profile

Light propagation in the four head models with and without the FS was predicted in order to evaluate the influence of the FS on the NIRS signal. The source at position A or B and detector were placed on the forehead of the model as shown in Fig. 2(b). In the case of source A, the FS existed inside the distribution of the light path connecting the source and detector, while the FS was almost outside of the light path in the case of source B.

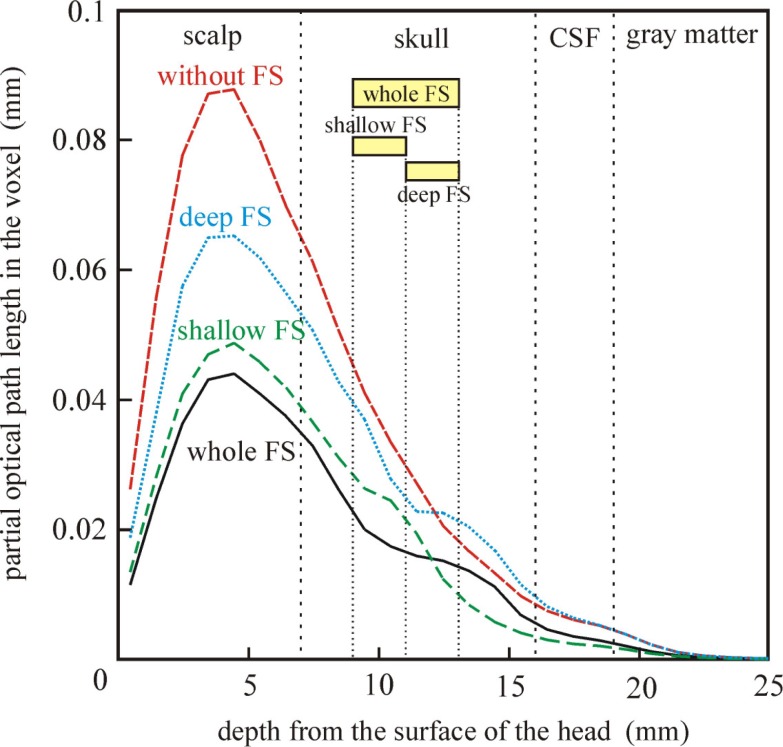
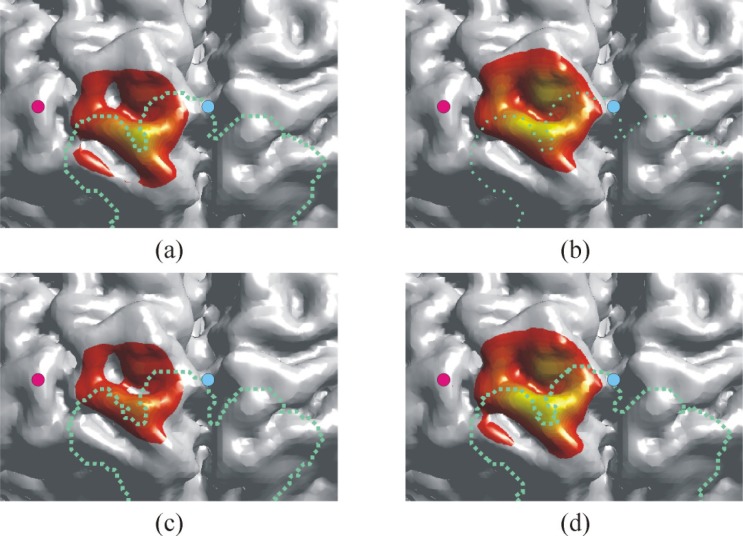
The spatial sensitivity profiles for the source at position A and detector in the four head models with parameter set (I) are shown in Fig. 5 . The spatial sensitivity profile is distorted by the FS and the distortion depends on the depth of the FS. In the models with the FS, the spatial sensitivity in the scalp around the midpoint between the source and detector is significantly reduced and the sensitivity around the FS increased. The depth profile of the spatial sensitivity along the line in Fig. 5 is shown in Fig. 6 . The whole FS and shallow FS reduce the penetration depth of the spatial sensitivity profile. The deep FS increases the penetration depth of the spatial sensitivity profile, however, the penetration depth in the gray matter is almost the same as that in the model without the FS. The spatial sensitivity profiles on the brain surface in the four models with parameter set (I) are shown in Fig. 7 . The dashed line indicates the position of the FS. A hypothetical position of the FS is also shown in the model without the FS for reference. The spatial sensitivity profile on the brain in the model without the FS shown in Fig. 7(b) is almost symmetrically distributed with respect to the line connecting the source and detector while that in the model with the whole FS shown in Fig. 7(a) is slightly shifted toward the lower side and the peak of the sensitivity is reduced. The spatial sensitivity is narrowed in the model with the shallow FS while the spatial sensitivity is broadened toward the lower side in the model with the deep FS. These results indicate that the increase in photon fluence around the FS affects the spatial sensitivity profile of the NIRS measurements.

Fig. 5.

Fig. 5

Open in a new tab

The influence of the FS on the spatial sensitivity profile for the source at position A and detector. (a) The model with the whole FS, (b) the model without the FS, (c) the model with the shallow FS, (d) the model with the deep FS. The line in the figures represents the position of the depth profile shown in Fig. 6.

Fig. 6.

Fig. 6

Open in a new tab

The depth profile of the spatial sensitivity profile in the four head models. The position of the profile is shown in Fig. 5.

Fig. 7.

Fig. 7

Open in a new tab

The influence of the frontal sinus on the spatial sensitivity profile on the brain surface. (a) The model with the whole FS, (b) the model without the FS, (c) the model with the shallow FS, (d) the model with the deep FS. Dashed line indicates the position of the FS.

The tendency of the influence of the FS can be quantitatively evaluated by the intensity and optical path length of the detected light shown in Table 2 . The partial optical path length in the scalp is reduced while that in the skull including the FS is increased in all the models with the FS. This indicates that the light which propagates through the FS tends to be detected by the detector. Since light propagates in straight line without absorption in the FS, the detected intensity is increased and the total optical path length is decreased by the presence of the FS. It should be noted that the partial optical path length in the FS is unexpectedly long although no scattering can occur in the FS. This indicates that many photons scattered in the skull passes through the FS without absorption. These photons increase the photon fluence around the FS. The influence of the FS on the partial optical path length in the gray matter depends on the depth of the FS. The deep FS increases the partial optical path length in the gray matter while the shallow FS decreases the partial optical path length in the gray matter.

Table 2. Intensity and path length of detected light for the head models with different types of FS.

Type of 
frontal sinus Detected intensity Total path 
length (mm) Partial optical path length (mm)
Scalp Skull FS CSF Gray matter White matter
(a) Whole FS 3.4 × 10−8 166 88.4 67.7 37.6 7.81 2.06 0.253
(b) Without FS 7.5 × 10−9 230 115 101 0 11.3 2.71 0.397
(c) Shallow FS 2.7 × 10−8 179 91.6 80.7 29.0 5.23 1.35 0.163
(d) Deep FS 1.3 × 10−8 210 100 94.7 16.6 12.4 3.01 0.404
Open in a new tab

Figure 8 shows the ratio of the partial optical path length in the gray matter for the head models with the FS to that for the head model without the FS. The results for the models with the three different parameter sets are compared in order to investigate the dependence of the influence of the FS on the optical properties of the head. In the head models with all the parameter sets, the deep FS increases and the shallow FS decreases the partial optical path length in the gray matter. However, in the case of the whole FS, the partial optical path length in the gray matter for the models with parameter sets (II) and (III) are increased by the influence of the FS while that in the model with parameter set (I) is decreased. The tendency of the influence of the FS in the head model with parameter set (III) is almost the same as that in the head model with parameter set (II). This result indicates that the influence of the FS on the NIRS signal depends on not only the depth of the FS but also the optical properties of the superficial tissues such as the scalp and skull.

Fig. 8.

Fig. 8

Open in a new tab

The influence of the optical properties of the head model on the partial optical path length in the gray matter. The partial optical path length in the gray matter for the head models with the FS is normalized by that for the head model without the FS. Each parameter set is listed in Table 1.

Figures 9(a) and 9(b) show the spatial sensitivity profiles for the source at position B and detector in the models (parameter set (I)) with the FS shown in Fig. 3(a) and without the FS shown in Fig. 3(b), respectively. The spatial sensitivity profile in the skull is significantly distorted toward the FS as shown in Fig. 9(a). Consequently, the spatial sensitivity profile on the brain surface is broadened toward the direction of the FS. The influence of the FS on the sensitivity of the NIRS signal depends on the relative position of the source-detector pair and the FS.

Fig. 9.

Fig. 9

Open in a new tab

The influence of the FS on the spatial sensitivity profile for the source at position B and detector. (a) The model with the whole FS. The FS is almost outside of the distribution of the light path connecting the source and detector. (b) The model without the FS.

4. Discussion

Light propagation in tissue is known to be strongly affected by the presence of voids and low-scattering regions. The light tends to propagate around the void region, and consequently, the spatial sensitivity around the void region is increased. In the brain activation measurements by NIRS, the low-scattering CSF affects light propagation in the head and increases the partial optical path length, i.e., the sensitivity of the NIRS signal, of the gray matter neighboring the CSF [14–16]. The FS also increases the spatial sensitivity around the FS, and consequently, decreases that apart from the FS. Since the brain is not next to the FS, the influence of the FS on the sensitivity of the NIRS signal is not consistent and is more complicated than that of the CSF. The influence of the FS on the sensitivity of the NIRS signal depends on the depth of the FS and the optical properties of the scalp and skull. The shallow FS decreases the sensitivity of the NIRS signal while the deep FS increases the sensitivity. The depth at which this inversion based on the influence of the FS occurred is changed by the optical properties of the scalp and skull. The optical properties of the tissues depend on the wavelength and the wide range of different values for the same type of tissues is obtained from the literature. The influence of the FS also depends on the relative position of the source-detector pair and FS. When the FS exists almost outside of the distribution of the light path connecting the source and the detector, the spatial sensitivity profile tends to be broadened. Furthermore, the realistic head models in this study do not consider the presence of the extra-cerebral vasculature, such as sagittal sinus. The influence of the sagittal sinus on the NIRS signal has been reported [21] and the sagittal sinus is located behind the middle of the FS. Careful consideration is needed to estimate the influence of the FS on the sensitivity of the NIRS signal.

The FS tends to locate below the eyebrows, and in this case, the influence of the FS on the NIRS measurements of the brain activation in the frontal area may be minimized by the optimal probe arrangement. However, the depth and size of the FS is different between individuals. It is necessary to analyze light propagation in the 3D head model, the anatomical structure of which is based on the structural image of the individual if you need to obtain details of the influence of the FS on the NIRS measurements.

5. Conclusions

The 3D realistic head models of which the structure is based on the MR and x-ray CT images are constructed to investigate the influence of a FS on the brain function measurements by near-infrared spectroscopy and imaging. Light propagation in the head model with the FS of which the geometry was based on the CT images was compared to that in the head models with the modified FS to investigate the influence of the FS on the NIRS signal. Light propagation in the head is strongly affected by the presence of the FS. The distribution of the photon fluence is broadened in the direction of the FS, consequently, the spatial sensitivity around the FS tends to be increased. Since the influence of the FS on light propagation in the brain depends on the depth of the FS and the optical properties of the scalp and skull, the influence of the FS on the sensitivity of the NIRS signal to the brain activation is not consistent across the source-detector pairs. The shallow FS tends to reduce the sensitivity of the NIRS signal, however, the deep FS can increase the sensitivity of the NIRS signal.

Acknowledgment

The authors thank Atsushi Tachibana for his technical support of the MRI scanning.

References and links

  • 1.Ferrari M., Quaresima V., “A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application,” Neuroimage (to be published). [DOI] [PubMed] [Google Scholar]
  • 2.Koizumi H., Yamamoto T., Maki A., Yamashita Y., Sato H., Kawaguchi H., Ichikawa N., “Optical topography: practical problems and new applications,” Appl. Opt. 42(16), 3054–3062 (2003). 10.1364/AO.42.003054 [DOI] [PubMed] [Google Scholar]
  • 3.Hoshi Y., Tsou B. H., Billock V. A., Tanosaki M., Iguchi Y., Shimada M., Shinba T., Yamada Y., Oda I., “Spatiotemporal characteristics of hemodynamic changes in the human lateral prefrontal cortex during working memory tasks,” Neuroimage 20(3), 1493–1504 (2003). 10.1016/S1053-8119(03)00412-9 [DOI] [PubMed] [Google Scholar]
  • 4.Taga G., Asakawa K., “Selectivity and localization of cortical response to auditory and visual stimulation in awake infants aged 2 to 4 months,” Neuroimage 36(4), 1246–1252 (2007). 10.1016/j.neuroimage.2007.04.037 [DOI] [PubMed] [Google Scholar]
  • 5.Uludağ K., Steinbrink J., Kohl-Bareis M., Wenzel R., Villringer A., Obrig H., “Cytochrome-c-oxidase redox changes during visual stimulation measured by near-infrared spectroscopy cannot be explained by a mere cross talk artefact,” Neuroimage 22(1), 109–119 (2004). 10.1016/j.neuroimage.2003.09.053 [DOI] [PubMed] [Google Scholar]
  • 6.Wabnitz H., Moeller M., Liebert A., Obrig H., Steinbrink J., Macdonald R., “Time-resolved near-infrared spectroscopy and imaging of the adult human brain,” Adv. Exp. Med. Biol. 662, 143–148 (2010). 10.1007/978-1-4419-1241-1_20 [DOI] [PubMed] [Google Scholar]
  • 7.Franceschini M. A., Joseph D. K., Huppert T. J., Diamond S. G., Boas D. A., “Diffuse optical imaging of the whole head,” J. Biomed. Opt. 11(5), 054007 (2006). 10.1117/1.2363365 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Wolf M., Ferrari M., Quaresima V., “Progress of near-infrared spectroscopy and topography for brain and muscle clinical applications,” J. Biomed. Opt. 12(6), 062104 (2007). 10.1117/1.2804899 [DOI] [PubMed] [Google Scholar]
  • 9.Sakatani K., Murata Y., Fujiwara N., Hoshino T., Nakamura S., Kano T., Katayama Y., “Comparison of blood-oxygen-level-dependent functional magnetic resonance imaging and near-infrared spectroscopy recording during functional brain activation in patients with stroke and brain tumors,” J. Biomed. Opt. 12(6), 062110 (2007). 10.1117/1.2823036 [DOI] [PubMed] [Google Scholar]
  • 10.Muehlschlegel S., Selb J., Patel M., Diamond S. G., Franceschini M. A., Sorensen A. G., Boas D. A., Schwamm L. H., “Feasibility of NIRS in the neurointensive care unit: a pilot study in stroke using physiological oscillations,” Neurocrit. Care 11(2), 288–295 (2009). 10.1007/s12028-009-9254-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Suto T., Fukuda M., Ito M., Uehara T., Mikuni M., “Multichannel near-infrared spectroscopy in depression and schizophrenia: cognitive brain activation study,” Biol. Psychiatry 55(5), 501–511 (2004). 10.1016/j.biopsych.2003.09.008 [DOI] [PubMed] [Google Scholar]
  • 12.Miyai I., Tanabe H. C., Sase I., Eda H., Oda I., Konishi I., Tsunazawa Y., Suzuki T., Yanagida T., Kubota K., “Cortical mapping of gait in humans: a near-infrared spectroscopic topography study,” Neuroimage 14(5), 1186–1192 (2001). 10.1006/nimg.2001.0905 [DOI] [PubMed] [Google Scholar]
  • 13.Watanabe E., Maki A., Kawaguchi F., Takashiro K., Yamashita Y., Koizumi H., Mayanagi Y., “Non-invasive assessment of language dominance with near-infrared spectroscopic mapping,” Neurosci. Lett. 256(1), 49–52 (1998). 10.1016/S0304-3940(98)00754-X [DOI] [PubMed] [Google Scholar]
  • 14.Okada E., Firbank M., Schweiger M., Arridge S. R., Cope M., Delpy D. T., “Theoretical and experimental investigation of near-infrared light propagation in a model of the adult head,” Appl. Opt. 36(1), 21–31 (1997). 10.1364/AO.36.000021 [DOI] [PubMed] [Google Scholar]
  • 15.Wolf M., Keel M., Dietz V., von Siebenthal K., Bucher H. U., Baenziger O., “The influence of a clear layer on near-infrared spectrophotometry measurements using a liquid neonatal head phantom,” Phys. Med. Biol. 44(7), 1743–1753 (1999). 10.1088/0031-9155/44/7/313 [DOI] [PubMed] [Google Scholar]
  • 16.Okada E., Delpy D. T., “Near-infrared light propagation in an adult head model. I. Modeling of low-level scattering in the cerebrospinal fluid layer,” Appl. Opt. 42(16), 2906–2914 (2003). 10.1364/AO.42.002906 [DOI] [PubMed] [Google Scholar]
  • 17.Boas D. A., Culver J. P., Stott J. J., Dunn A. K., “Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head,” Opt. Express 10(3), 159–170 (2002). [DOI] [PubMed] [Google Scholar]
  • 18.Fukui Y., Ajichi Y., Okada E., “Monte Carlo prediction of near-infrared light propagation in realistic adult and neonatal head models,” Appl. Opt. 42(16), 2881–2887 (2003). 10.1364/AO.42.002881 [DOI] [PubMed] [Google Scholar]
  • 19.Kawaguchi H., Koyama T., Okada E., “Effect of probe arrangement on reproducibility of images by near-infrared topography evaluated by a virtual head phantom,” Appl. Opt. 46(10), 1658–1668 (2007). 10.1364/AO.46.001658 [DOI] [PubMed] [Google Scholar]
  • 20.Heiskala J., Hiltunen P., Nissilä I., “Significance of background optical properties, time-resolved information and optode arrangement in diffuse optical imaging of term neonates,” Phys. Med. Biol. 54(3), 535–554 (2009). 10.1088/0031-9155/54/3/005 [DOI] [PubMed] [Google Scholar]
  • 21.Dehaes M., Gagnon L., Lesage F., Pélégrini-Issac M., Vignaud A., Valabrègue R., Grebe R., Wallois F., Benali H., “Quantitative investigation of the effect of the extra-cerebral vasculature in diffuse optical imaging: a simulation study,” Biomed. Opt. Express 2(3), 680–695 (2011). 10.1364/BOE.2.000680 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Okada E., Yamamoto D., Kiryu N., Katagiri A., Yokose N., Awano T., Igarashi K., Nakamura S., Hoshino T., Murata Y., Kano T., Sakatani K., Katayama Y., “Theoretical and experimental investigation of the influence of frontal sinus on the sensitivity of the NIRS signal in the adult head,” Adv. Exp. Med. Biol. 662, 231–236 (2010). 10.1007/978-1-4419-1241-1_33 [DOI] [PubMed] [Google Scholar]
  • 23.Ashburner J., “A fast diffeomorphic image registration algorithm,” Neuroimage 38(1), 95–113 (2007). 10.1016/j.neuroimage.2007.07.007 [DOI] [PubMed] [Google Scholar]
  • 24.Thiran J., Warscotte V., Macq B., “A queue-based region growing algorithm for accurate segmentation of multi-dimensional digital images,” Signal Process. 60(1), 1–10 (1997). 10.1016/S0165-1684(97)00060-1 [DOI] [Google Scholar]
  • 25.Simpson C. R., Kohl M., Essenpreis M., Cope M., “Near-infrared optical properties of ex vivo human skin and subcutaneous tissues measured using the Monte Carlo inversion technique,” Phys. Med. Biol. 43(9), 2465–2478 (1998). 10.1088/0031-9155/43/9/003 [DOI] [PubMed] [Google Scholar]
  • 26.Firbank M., Hiraoka M., Essenpreis M., Delpy D. T., “Measurement of the optical properties of the skull in the wavelength range 650-950 nm,” Phys. Med. Biol. 38(4), 503–510 (1993). 10.1088/0031-9155/38/4/002 [DOI] [PubMed] [Google Scholar]
  • 27.van der Zee P., Essenpreis M., Delpy D. T., “Optical properties of brain tissue,” Proc. SPIE 1888, 454–465 (1993). 10.1117/12.154665 [DOI] [Google Scholar]
  • 28.Roggan A., Minet O., Shröder C., Müller G., “The determination of optical tissue properties with double integrating sphere technique and Monte Carlo simulation,” Proc. SPIE 2100, 42–56 (1994). 10.1117/12.179026 [DOI] [Google Scholar]
  • 29.Yaroslavsky A. N., Schulze P. C., Yaroslavsky I. V., Schober R., Ulrich F., Schwarzmaier H.-J., “Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range,” Phys. Med. Biol. 47(12), 2059–2073 (2002). 10.1088/0031-9155/47/12/305 [DOI] [PubMed] [Google Scholar]
  • 30.Wilson B. C., Adam G., “A Monte Carlo model for the absorption and flux distributions of light in tissue,” Med. Phys. 10(6), 824–830 (1983). 10.1118/1.595361 [DOI] [PubMed] [Google Scholar]
  • 31.Hiraoka M., Firbank M., Essenpreis M., Cope M., Arridge S. R., van der Zee P., Delpy D. T., “A Monte Carlo investigation of optical pathlength in inhomogeneous tissue and its application to near-infrared spectroscopy,” Phys. Med. Biol. 38(12), 1859–1876 (1993). 10.1088/0031-9155/38/12/011 [DOI] [PubMed] [Google Scholar]
  • 32.Wang L., Jacques S. L., Zheng L., “MCML—Monte Carlo modeling of light transport in multi-layered tissues,” Comput. Methods Programs Biomed. 47(2), 131–146 (1995). 10.1016/0169-2607(95)01640-F [DOI] [PubMed] [Google Scholar]

Articles from Biomedical Optics Express are provided here courtesy of Optica Publishing Group

RESOURCES