Table 1. Indicators considered in this paper.

Name of indicator	Interpretation	Symbol	NonparametricEstimate
Conditionalvariance	Variance of x as a function of x. We use the conditional variance as an approximation of thelong-run stationary variance of x, 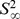. In a critical transition caused by a local co-dimensionone bifurcation of the drift function, the long-run stationary variance of the linearizationaround the deterministic steady state becomes infinite at the transition point. The long runstationary variance may increase as a noise-induced transition is approached.	S2	Equation [5]
Diffusion	Variance of dx as a function of x. We use the estimator as an approximation of 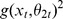as defined near equation [1]. In a noise-induced transition, the variance matrix functiong’g (or g2) increases as the transition is approached.	g’g, or g2	Equation [7]