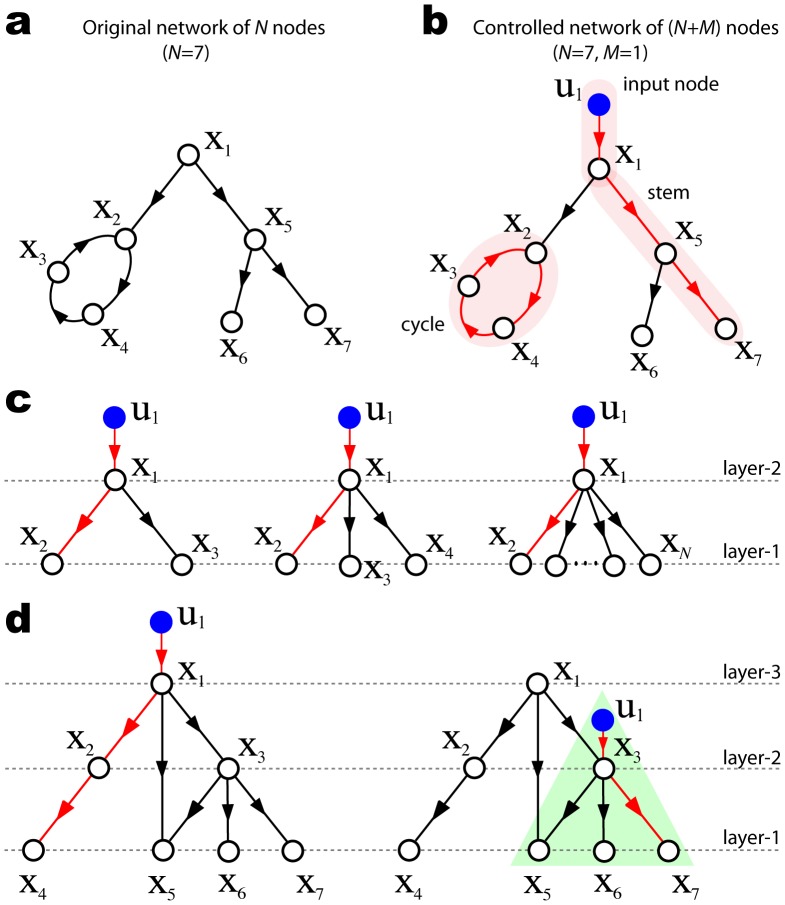
Figure 1. Control centrality.
(a) A simple network of 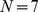 nodes. (b) The controlled network is represented by a directed graph
nodes. (b) The controlled network is represented by a directed graph 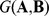 with an input node
with an input node 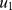 connecting to a state node
connecting to a state node  . The stem-cycle disjoint subgraph
. The stem-cycle disjoint subgraph 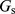 (shown in red) contains six edges, which is the largest number of edges among all possible stem-cycle disjoint subgraphs of the directed graph
(shown in red) contains six edges, which is the largest number of edges among all possible stem-cycle disjoint subgraphs of the directed graph 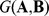 and corresponds to the generic dimension of controllable subspace by controlling node
and corresponds to the generic dimension of controllable subspace by controlling node 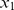 . The control centrality of node
. The control centrality of node  is thus
is thus 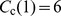 . (c) The control centrality of the central hub in a directed star is always 2 for any network size
. (c) The control centrality of the central hub in a directed star is always 2 for any network size 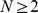 . (d) The control centrality of a node in a directed acyclic graph (DAG) equals its layer index. In applying Hosoe’s theorem, if not all state nodes are accessible, we just need to consider the accessible part (highlighted in green) of the input node(s).
. (d) The control centrality of a node in a directed acyclic graph (DAG) equals its layer index. In applying Hosoe’s theorem, if not all state nodes are accessible, we just need to consider the accessible part (highlighted in green) of the input node(s).