Abstract
The design of molecular electrocatalysts for H2 oxidation and production is important for the development of alternative renewable energy sources that are abundant, inexpensive, and environmentally benign. Recently, nickel-based molecular electrocatalysts with pendant amines that act as proton relays for the nickel center were shown to effectively catalyze H2 oxidation and production. We developed a quantum mechanical approach for studying proton-coupled electron transfer processes in these types of molecular electrocatalysts. This theoretical approach is applied to a nickel-based catalyst in which phosphorous atoms are directly bonded to the nickel center, and nitrogen atoms of the ligand rings act as proton relays. The catalytic step of interest involves electron transfer between the nickel complex and the electrode as well as intramolecular proton transfer between the nickel and nitrogen atoms. This process can occur sequentially, with either the electron or proton transferring first, or concertedly, with the electron and proton transferring simultaneously without a stable intermediate. The electrochemical rate constants are calculated as functions of overpotential for the concerted electron-proton transfer reaction and the two electron transfer reactions in the sequential mechanisms. Our calculations illustrate that the concerted electron-proton transfer standard rate constant will increase as the equilibrium distance between the nickel and nitrogen atoms decreases and as the pendant amines become more flexible to facilitate the contraction of this distance with a lower energy penalty. This approach identifies the favored mechanisms under various experimental conditions and provides insight into the impact of substituents on the nitrogen and phosphorous atoms.
Keywords: hydrogen evolution, heterogeneous catalysis, PCET
Environmental and economic concerns about the use of fossil fuels have led to the development of new technologies that are more environmentally friendly but are also cost-effective alternatives to nonrenewable resources. An important example is the oxidation and production of H2 for use in hydrogen-based fuel cells and functional storage devices for the energy harvested from solar, wind, and other environmentally benign processes (1). While efficient methods have been developed for H2 oxidation and production, platinum catalysts are neither abundant enough nor cost effective enough for mass production and large-scale use (2). On the other hand, H2 oxidation and production occur naturally in the hydrogenase class of enzymes. These biological systems could serve as the key to the design of effective synthetic catalysts because the catalytic center of the enzyme is comprised of iron and/or nickel, both of which are highly abundant and inexpensive metals.
The presence of an amine ligand in the second coordination sphere is thought to contribute significantly to the high catalytic activity of the [FeFe] hydrogenase enzymes. These pendant amines may assist in the heterolytic cleavage of H2 by facilitating proton transfer reactions as well as coupling electron and proton transfer reactions (3, 4). While the relatively high turnover frequency and low required overpotential of hydrogenase enzymes (5–7) make them ideal candidates for use in large-scale oxidation and production of H2, the functionality of the catalytic center is usually lost when removed from the surrounding protein, and synthesis of the entire enzyme is not practical. Thus, significant efforts have been directed toward the design of molecular catalysts that mimic the catalytic center of hydrogenase enzymes.
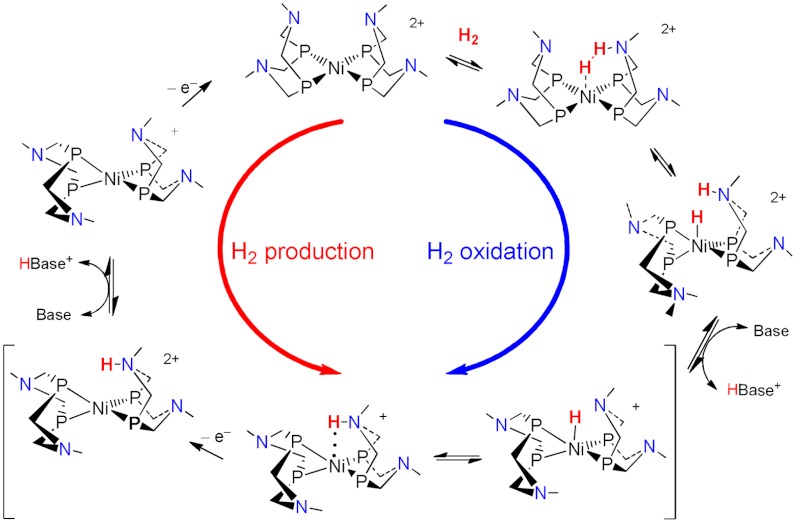
Recently, DuBois and coworkers have designed molecular electrocatalysts that incorporate pendant amines to act as proton relays for the Ni center (3–5, 8). In the P2N2 systems, 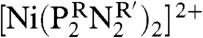 , the phosphorus atoms are directly bonded to the nickel center, and the nitrogen atoms of the ligand rings are in the second coordination sphere to enable them to act as proton relays. The proposed electrocatalytic cycle for these catalysts is depicted in Fig. 1, where the clockwise direction corresponds to H2 oxidation and the counterclockwise direction corresponds to H2 production. Experiments indicate that these complexes can produce H2 at turnover frequencies as large as 103–105 s-1 with low to moderate overpotentials (8–10). Moreover, these catalysts can be tailored for H2 oxidation or production by altering the substituents on the P and N atoms. While much is known about the thermodynamic properties of these species with different substituents (11), significantly less is known about their detailed mechanisms and kinetics. Understanding the factors that control the flow of electrons and protons in these systems is crucial to developing better catalysts.
, the phosphorus atoms are directly bonded to the nickel center, and the nitrogen atoms of the ligand rings are in the second coordination sphere to enable them to act as proton relays. The proposed electrocatalytic cycle for these catalysts is depicted in Fig. 1, where the clockwise direction corresponds to H2 oxidation and the counterclockwise direction corresponds to H2 production. Experiments indicate that these complexes can produce H2 at turnover frequencies as large as 103–105 s-1 with low to moderate overpotentials (8–10). Moreover, these catalysts can be tailored for H2 oxidation or production by altering the substituents on the P and N atoms. While much is known about the thermodynamic properties of these species with different substituents (11), significantly less is known about their detailed mechanisms and kinetics. Understanding the factors that control the flow of electrons and protons in these systems is crucial to developing better catalysts.
Fig. 1.
Proposed reversible mechanism of H2 oxidation (clockwise) and H2 production (counterclockwise) for the  class of molecular electrocatalysts. The brackets indicate the steps of interest. The substituents on P and N are not shown for clarity. Figure originally provided by R. M. Bullock. Reprinted with permission from (20), Copyright 2012 American Chemical Society.
class of molecular electrocatalysts. The brackets indicate the steps of interest. The substituents on P and N are not shown for clarity. Figure originally provided by R. M. Bullock. Reprinted with permission from (20), Copyright 2012 American Chemical Society.
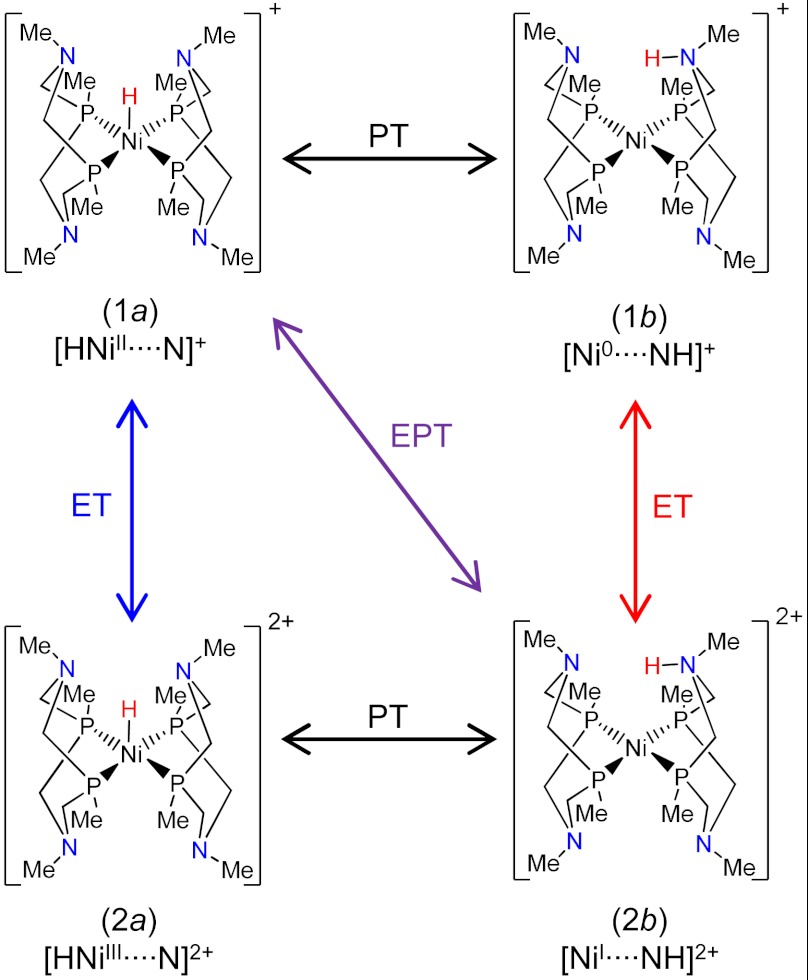
The objective of this paper is to examine the mechanism of proton-coupled electron transfer (12–19) in these molecular electrocatalysts. We focus on the steps identified with brackets in Fig. 1 for the species with methyl substituents on the P and N atoms and all cyclic ligands in the boat conformation. The bracketed catalytic steps involve electron transfer (ET) between the Ni complex and the electrode as well as proton transfer (PT) between the Ni and the N. The net reaction of interest is [HNiII(P2N2)2]+ - e- → [NiI(P2HN2)(P2N2)]2+ for H2 oxidation and the reverse reaction for H2 production. This process can be described in terms of the four diabatic states depicted in Fig. 2 (13, 14). For H2 oxidation, the sequential ET-PT mechanism corresponds to (1a) → (2a) → (2b), the sequential PT-ET mechanism corresponds to (1a) → (1b) → (2b), and the concerted electron-proton transfer (EPT) mechanism corresponds to (1a) → (2b). For H2 production, the steps within these mechanisms occur in the reverse order.
Fig. 2.
Schematic depiction of the states and charge transfer reactions involved in the proton-coupled electron transfer process of interest, corresponding to the bracketed steps in Fig. 1. The complex shown has methyl substituents on the P and N atoms with all rings in the boat conformation. The ET, PT, and EPT reactions are shown for H2 oxidation, (1a) → (2b), and H2 production, (2b) → (1a).
In previous work (20), we explored the thermodynamics of the concerted and sequential mechanisms and the kinetics of the PT reactions for this part of the catalytic cycle. In the present paper, we examine the kinetics of the concerted EPT reaction as well as the kinetics of the ET reactions involved in the sequential mechanisms. In particular, we use quantum mechanical methods to calculate the electrochemical rate constants for ET and concerted EPT as functions of overpotential. These Tafel plots assist in the identification of the favored mechanism under various experimental conditions. We also discuss the qualitative impact of substituents on these Tafel plots and the connection between these diagrams and experimental data generated with cyclic voltammetry. The general theoretical approach presented herein is applicable to a wide range of molecular electrocatalysts and could potentially play a significant role in catalyst design.
Results and Discussion
We calculated the electrochemical nonadiabatic rate constants for ET and EPT using a theoretical framework based on Marcus theory (21). The anodic and cathodic nonadiabatic rate constants for ET are:
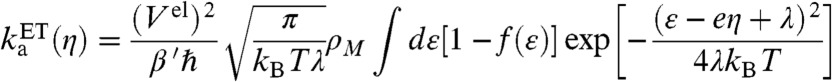 |
[1] |
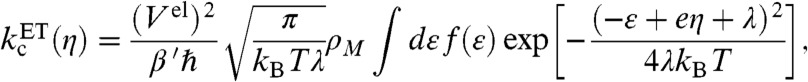 |
[2] |
where f(ε) is the Fermi distribution function for the electronic states in the electrode; ρM is the density of states at the Fermi level, which is assumed to be a constant in the vicinity of the Fermi level; Vel is the electronic coupling; β′ is a parameter of magnitude ∼1–3 Å-1 representing the exponential decay of the electronic coupling with the distance between the molecule and the electrode; and λ is the reorganization energy.
For fixed proton donor-acceptor distance R, the anodic and cathodic nonadiabatic rate constants for concerted EPT are (22–24):
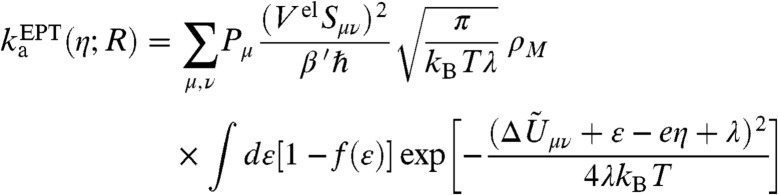 |
[3] |
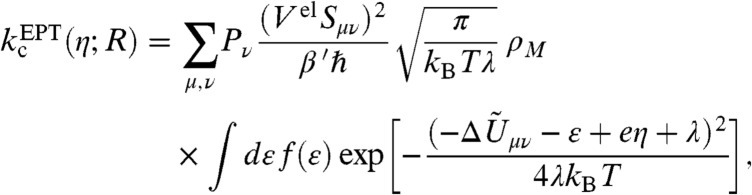 |
[4] |
where the summations are over proton vibrational states μ of the reduced solute complex and ν of the oxidized solute complex. Pμ and Pν are the Boltzmann probabilities for the proton vibrational states μ and ν, and Sμν is the overlap integral between the proton vibrational wavefunctions μ and ν. The quantity  is defined to be
is defined to be  , where ΔUμν is the energy difference between states ν and μ, and QI and QII are the vibrational partition functions of the reduced and oxidized solute complexes, respectively, in bulk solution. The quantities Pμ, Sμν, and
, where ΔUμν is the energy difference between states ν and μ, and QI and QII are the vibrational partition functions of the reduced and oxidized solute complexes, respectively, in bulk solution. The quantities Pμ, Sμν, and 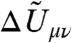 depend on the proton donor-acceptor distance R.
depend on the proton donor-acceptor distance R.
The effects of the proton donor-acceptor motion can be included by thermally averaging over the proton donor-acceptor distance (25–27):
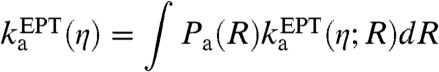 |
[5] |
and the analogous expression for the cathodic rate constant, where Pa(R) and Pc(R) are probability distribution functions for the anodic and cathodic processes, respectively. In the present work, these probability distribution functions are chosen to correspond to a classical harmonic oscillator and depend on an effective force constant keff and equilibrium proton donor-acceptor distance 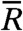 . Note that anharmonic probability distribution functions could be obtained from electronic structure calculations and/or molecular dynamics simulations. The computational methods used to calculate the input quantities for the above rate constant expressions are described in the Methods section.
. Note that anharmonic probability distribution functions could be obtained from electronic structure calculations and/or molecular dynamics simulations. The computational methods used to calculate the input quantities for the above rate constant expressions are described in the Methods section.
In this paper, for a given ET or EPT reaction, the standard potential corresponds to the potential at which the anodic and cathodic rate constants are identical, and the standard rate constant is the rate constant at the standard potential. To avoid the calculation of some of the quantities in the prefactors of the rate constant expressions, we calculate the rate constants relative to the standard rate constant of a specified reaction (i.e., ratios of rate constants). The overpotential η is defined as the applied potential relative to the standard potential of a specified reaction (i.e., differences between potentials).
The main differences between the EPT and ET rate constant expressions are that the EPT rate constant expressions require a summation over the reactant and product proton vibrational states, and each term is proportional to the Boltzmann population of the reactant proton vibrational state and the square of the overlap between the reactant and product proton vibrational wavefunctions. In addition, the effective activation energy in the exponential depends on the difference between the product and reactant proton vibrational state energies. All of these quantities depend strongly on the proton donor-acceptor distance, which for these systems is the Ni-N distance. Thus, the calculation of the EPT rate constant requires the generation of proton potentials for a range of Ni-N distances. For simplicity, we calculate only one-dimensional proton potentials and proton vibrational wavefunctions along an axis connecting the equilibrium positions of the transferring hydrogen in the reduced and oxidized states for each Ni-N distance, as depicted at the top of Fig. 3. In principle, the three-dimensional analogs could be generated, but the qualitative trends are expected to be captured with the one-dimensional treatment of proton motion.
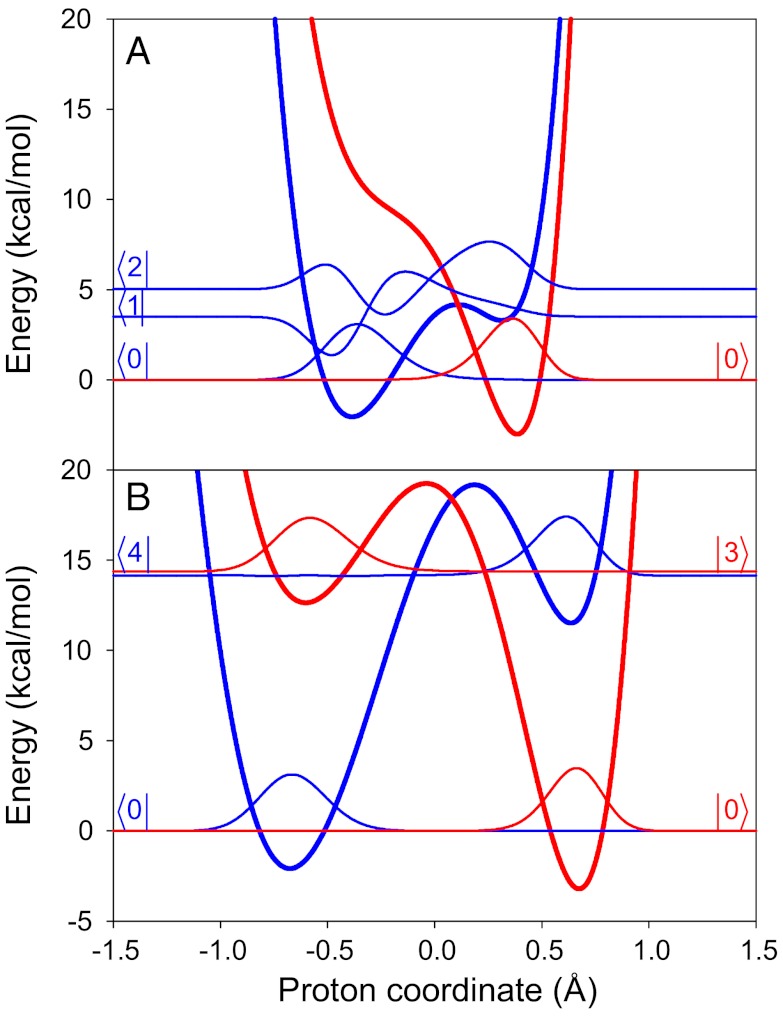
Fig. 3.
At the top, average equilibrium structure of the catalyst, identifying the Ni (dark pink) and N (dark blue) atoms involved in the PT reaction, as well as the proton axis used for generation of the proton potentials. The hydrogen atom is shown at its equilibrium position for both the reduced and oxidized states (i.e., bound to the Ni and N atoms in the (1a) and (2b) states, respectively). In the calculations, only one hydrogen atom is included here and is moved along the proton axis to generate the proton potentials. In the lower portion, proton potentials for (A) the reduced state and (B) the oxidized state of the catalyst for the average structures at Ni-N distances of 2.94, 3.04, 3.14, and 3.25 Å. As the Ni-N distance decreases, the separation between the minima and the barrier for each proton potential decrease.
Fig. 3 depicts the proton potentials for the reduced and oxidized states of the complexes at Ni-N distances of 2.94, 3.04, 3.14, and 3.25 Å. The proton potentials for the reduced and oxidized states are highly asymmetric, where the minimum near the Ni is lower in energy for the reduced state and the minimum near the N is lower in energy for the oxidized state. Furthermore, as the Ni-N distance decreases, the separation between the minima and the barrier for each proton potential decrease. The ground state and selected excited state proton vibrational wavefunctions are depicted for the Ni-N distances of 2.94 Å and 3.25 Å in Fig. 4. As the Ni-N distance decreases, the proton vibrational wavefunctions become more delocalized, and the overlap between the ground state reactant and product proton vibrational wavefunctions increases significantly. As a result, the lower vibrational states contribute more to the rate constant as the Ni-N distance decreases.
Fig. 4.
Proton potentials and corresponding vibrational wavefunctions for the contributing proton vibrational states (as given in Table 1) for the reduced state (blue) and the oxidized state (red) for the average structures at (A) the Ni-N distance of 2.94 Å and (B) the average equilibrium Ni-N distance of 3.25 Å.
The overall EPT rate constant is determined by integrating the R-dependent rate constant over all values of R, weighting the rate constant by the probability of sampling each value of R. The average equilibrium Ni-N distance for the optimized reduced and oxidized complexes is 3.25 Å. The Gaussian probability distribution function, Pa(R) ≡ Pc(R), is chosen to be greatest at this average equilibrium distance in the approach used to generate the results presented below. (The results from an alternative approach that uses different probability functions for the anodic and cathodic rate constants are presented in the SI Appendix). On the other hand, the rate constant increases as R decreases because of the greater contributions from the lower vibrational states due to the larger overlap integrals. Thus, the dominant Ni-N distance (i.e., the distance that contributes the most to the overall rate constant) is determined by a competition between the rate constant increasing and the probability distribution function decreasing as R decreases. For this system, the dominant Ni-N distance is found to be 3.00 Å. This dominant distance is significantly smaller than the equilibrium Ni-N distances of 3.31 and 3.20 Å for the optimized reduced and oxidized complexes, respectively.
A more detailed analysis can be performed using the data in Table 1. At each Ni-N distance, the standard rate constant is determined by a balance among the Boltzmann populations of the reactant states, the free energy barriers, and the overlaps between the reactant and product proton vibrational wavefunctions. At the average equilibrium Ni-N distance of 3.25 Å, the main contributions to the standard rate constant arise from the 0/3 pair (i.e., the ground reactant state and the third excited product state) and the 4/0 pair (i.e., the fourth excited reactant state and the ground product state). As depicted in Fig. 4, the overlap integrals between the proton vibrational wavefunctions for these pairs of reactant/product states are nearly unity because the excited reactant (product) state is localized on the same side as the ground product (reactant) state for the 4/0 (0/3) pair of states. On the other hand, the Boltzmann population of the fourth excited reactant state is 10-11, and the free energy barrier corresponding to the 0/3 pair of reactant/product states is very high, leading to a relatively small rate constant at this distance.
Table 1.
Analysis of main contributions to the standard rate constant for several Ni-N distances
| R(Å) * | μ/ν † | Pμ ‡ |
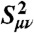 §
§
|
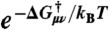 ¶
¶
|
% contrib.∥ |
| 2.94 | 1/0 | 2.7 × 10-3 | 0.065 | 5.3 × 10-4 | 30 |
| 2/0 | 2.1 × 10-4 | 0.587 | 1.5 × 10-3 | 61 | |
| 3.04 | 2/0 | 3.8 × 10-6 | 0.215 | 6.8 × 10-3 | 42 |
| 3/0 | 1.3 × 10-6 | 0.571 | 9.8 × 10-3 | 55 | |
| 3.25 | 0/3 | 1.0 | 0.855 | 5.1 × 10-12 | 40 |
| 4/0 | 4.3 × 10-11 | 0.917 | 1.6 × 10-1 | 58 |
*The Ni-N distance of 2.94 Å is the shortest distance examined. The intermediate Ni-N distance of 3.04 Å is 0.04 Å larger than the dominant distance, and the Ni-N distance of 3.25 Å is the average equilibrium distance.
†μ and ν correspond to the proton vibrational states for the reduced and oxidized states, respectively, of the catalyst.
‡Pμ is the Boltzmann probability for state μ.
§Sμν is the overlap integral between the proton vibrational wavefunctions associated with states μ and ν.
¶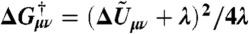 and is the effective free energy barrier at η = ε = 0.
and is the effective free energy barrier at η = ε = 0.
∥% contrib. is the percentage contribution to the overall standard rate constant at that distance R, 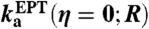 , including only contributions greater than 10%.
, including only contributions greater than 10%.
In contrast, at the shorter Ni-N distance of 2.94 Å, the main contributions to the standard rate constant arise from the 1/0 and 2/0 pairs of states (i.e., the first and second excited reactant states in conjunction with the ground product state). As depicted in Fig. 4, these reactant states have substantial probability on the donor side (i.e., near the Ni) but are delocalized enough to have significant overlap with the ground product state, which is localized on the acceptor side (i.e., near the N). The corresponding Boltzmann populations and free energy barriers are moderate, leading to significant contributions from both pairs of states. At the slightly larger Ni-N distance of 3.04 Å, which is only 0.04 Å larger than the dominant distance, the behavior is qualitatively similar, except the main contributions to the standard rate constant arise from the 2/0 and 3/0 pairs of states.
Based on this analysis, the standard rate constant at the dominant Ni-N distance of 3.00 Å is approximately 9,000 times greater than that at the average equilibrium Ni-N distance of 3.25 Å. On the other hand, the probability of sampling the smaller Ni-N distance is approximately 20 times smaller than that at the average equilibrium Ni-N distance. Thus, the contribution to the overall standard rate constant is approximately 450 times greater for the dominant Ni-N distance than for the average equilibrium Ni-N distance. This analysis illustrates that the rate constant is determined by a complex balance among various competing factors. The rate constant at each Ni-N distance is strongly influenced by the overlaps between the reactant and product proton vibrational wavefunctions, favoring the smaller Ni-N distances. On the other hand, the contribution of a particular Ni-N distance to the overall rate constant is strongly influenced by the probability of sampling that particular distance, favoring Ni-N distances closer to the equilibrium values.
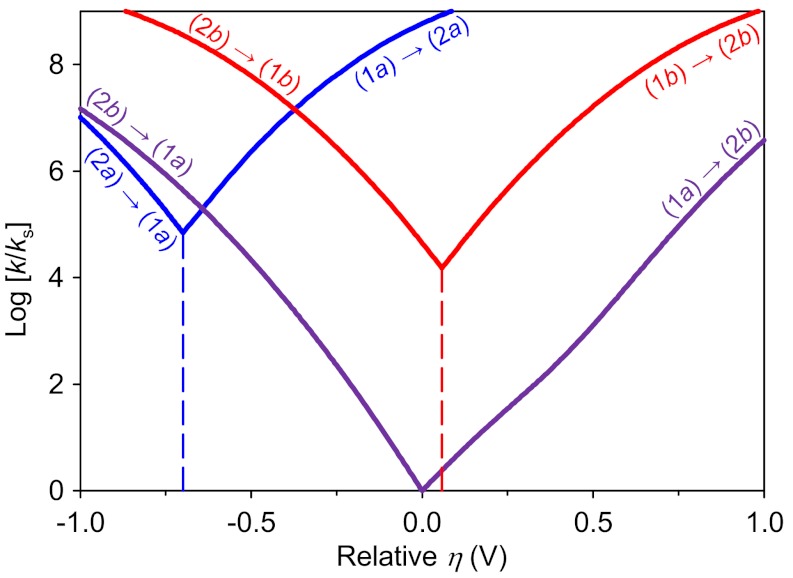
We calculated the electrochemical rate constants as functions of overpotential for the EPT and ET reactions using the rate constant expressions given above. For each reaction, the standard electrode potential, at which the anodic and cathodic rate constants are identical, is different. The differences between the standard potentials can be determined by the relative free energy changes for the reactions. Previously, we calculated the reduction potentials to be 0.01, 0.77, and 0.71 V vs. Fc+/Fc (ferrocenium/ferrocene) in acetonitrile for (1a) → (2a), (1b) → (2b), and (1a) → (2b), respectively (20). To compare the ET and EPT rate constants, Fig. 5 depicts the electrochemical rate constants as functions of the potential. Note that the EPT reaction is assumed to have a standard potential at η = 0, and the standard potentials for the two ET reactions (i.e., the minima of the curves) are shifted relative to this value according to the calculated reduction potentials. Thus, the overpotential η in Fig. 5 is defined to be the applied potential relative to the standard potential for the EPT reaction.
Fig. 5.
Electrochemical rate constants as functions of potential for the ET and EPT reactions of interest. The rate constants are given relative to ks, the standard rate constant for the EPT reaction. The standard potential for the EPT reaction is chosen to be zero overpotential (η = 0), and the standard potentials for the ET reactions are shifted relative to this value by their relative reduction potentials. Thus, the overpotential η is defined to be the applied potential relative to the standard potential for the EPT reaction. The curves are labeled according to the specific ET and EPT reactions.
The anodic EPT rate constant in Fig. 5 exhibits slightly unusual curvature in the region 0.4 < η < 0.7 V. This behavior is observed because the relative contributions from the various pairs of proton vibrational states depend on the overpotential. In the region η < 0.4 V, the dominant Ni-N distance is approximately 3.0 Å, and the main contributions to the rate constant arise from the 2/0 and 3/0 pairs of states, where the reactant and product vibrational states are localized predominantly on different sides. In the region η > 0.7 V, the dominant Ni-N distance is only slightly shorter than 3.25 Å, and the main contributions to the rate constant arise from the 0/3 pair of states, where the reactant and product states are both localized on the same side. This qualitative change occurs because application of a significant positive overpotential decreases the effective free energy barrier corresponding to the 0/3 pair of states. The intermediate regime of overpotential has significant contributions from the 2/0, 3/0, and 0/3 pairs of states in varying amounts. The cathodic EPT rate constant does not exhibit this qualitative change in contributions for the region of overpotential studied. This behavior is system dependent and will not always be observed for EPT reactions. Further analysis of the contributions to the rate constant at various values of η is available in the SI Appendix.
Fig. 5 illustrates that the relative values of the electrochemical rate constants for the two ET reactions and the EPT reaction depend strongly on the overpotential. For relatively negative overpotentials, the rate constant is greatest for the (2b) → (1b) ET reaction, and for relatively positive overpotentials, the rate constant is greatest for the (1a) → (2a) ET reaction. The regions in which each mechanism is dominant depend on the relative standard rate constants (i.e., the shifts along the y-axis) and the relative reduction potentials (i.e., the shifts along the x-axis). The standard rate constants for the two ET reactions are similar, with the minor difference arising from the smaller inner-sphere reorganization energy of 0.52 eV for (1a) → (2a) compared to 0.67 eV for (1b) → (2b). The standard rate constant for the EPT reaction is smaller than the standard rate constants for the two ET reactions mainly because of the Franck-Condon overlap factor (i.e., the square of the overlap between the reactant and product proton vibrational wavefunctions) in the EPT rate constant expression. In other words, the transfer of the proton imposes a penalty on the rate constant, but altering the applied overpotential can make EPT more favorable than ET. For example, the EPT rate constant is greater than the (2a) → (1a) ET rate constant at relatively negative overpotentials.
The Tafel plots in Fig. 5 can be altered by modifying the substituents on the P and N atoms in the Ni catalysts. In particular, the curves can be shifted along the x-axis by altering the relative reduction potentials and along the y-axis by altering the standard rate constants. Previously, we studied the impact of phenyl and benzyl substitutions on the reduction potentials for the ET and EPT reactions (20). For the nickel complex in which all methyl groups are replaced by phenyl groups and the rings are in the boat-chair conformation, the reduction potentials were calculated to be −0.78, 0.26, and −0.02 V vs. Fc+/Fc in acetonitrile for (1a) → (2a), (1b) → (2b), and (1a) → (2b), respectively (20). Assuming that the standard rate constants do not change, the resulting plot would resemble Fig. 5 except the (1b)↔(2b) curve would be shifted by 0.22 V in the direction of positive overpotential. The relative standard rate constants for the two ET reactions can be tweaked slightly by changing the inner-sphere reorganization energies. The relative standard rate constant for the EPT reaction can be altered by changing the proton potentials. As discussed above, however, the impact of the proton potential on the overall EPT rate constant is a complex balance of many factors, so the prediction of substituent effects on the EPT standard rate constant requires calculations such as those described herein. Our analysis illustrates, however, that the EPT standard rate constant will increase as the equilibrium Ni-N distance decreases and as the frequency of the Ni-N motion decreases (i.e., more mobile ligands will facilitate the contraction of the Ni-N distance, thereby increasing the overlaps). The incorporation of more flexible pendant amines should enable the N to approach the Ni more closely with a lower energy penalty. Note that the pendant amine must still remain in the vicinity of the Ni center for effective catalysis.
The direct comparison between these calculations and experimental data will require the calculation of relative current densities, which depend on the concentrations of the four species depicted in Fig. 2. In principle, the electrochemical rate constants given in Fig. 5 can be combined with a specific kinetic scheme to calculate the relative current densities for the two ET reactions and the EPT reaction. Such a treatment would involve information about the PT reactions as well (20). These data could also be used to simulate cyclic voltammograms for these catalysts, thereby enabling a direct comparison to accessible experimental data. These directions will be the focus of future research in efforts to design more effective catalysts.
While significant insights can be gained by examining the steps indicated in brackets in Fig. 1, the study of only one or two steps in the catalytic cycle does not provide a complete understanding of H2 oxidation or production. All steps in the catalytic cycle must be investigated to obtain complete information for designing more effective nickel-based electrocatalysts. For example, although more flexible pendant amines may be favorable for the proton-coupled electron transfer steps, they may adversely affect other steps in the catalytic cycle. Typically, the other steps in the cycle can be studied with more traditional electronic structure methods. The theoretical approach presented in this paper for studying the steps involving the coupling of electron and proton transfer is essential for obtaining a complete picture of the catalytic cycle. This theoretical approach is also applicable to the design of other molecular electrocatalysts.
Methods
The density of states, electronic coupling, and parameter β′ were assumed to be the same for ET and EPT reactions and therefore were not required for the calculation of relative rate constants. The outer-sphere (solvent) reorganization energy λs was assumed to be the same for ET and EPT reactions and was previously calculated to be λs = 0.39 eV for these systems using a dielectric continuum model, in which the nickel complex is enclosed in a spherical cavity on the surface of the electrode and immersed in the acetonitrile solvent (20, 28). The inner-sphere reorganization energy λi was previously calculated to be 0.52 eV for (1a) → (2a) and 0.67 eV for (1b) → (2b) and (1a) → (2b) for these systems (20). The total reorganization energy λ is the sum of the inner- and outer-sphere reorganization energies.
The quantities Pμ, Sμν, and 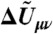 were calculated from a series of proton potentials determined at different proton donor-acceptor distances. In the present work, the proton potentials were obtained for structures generated by averaging the reduced and oxidized structures calculated from geometry optimizations with a constrained Ni-N distance. Average structures were obtained for Ni-N distances of 2.94, 3.04, 3.14, and 3.25 Å. The proton potentials were generated on a one-dimensional grid connecting the optimized hydrogen position for the reduced and oxidized states for each Ni-N distance, as depicted at the top of Fig. 3. The rate constants,
were calculated from a series of proton potentials determined at different proton donor-acceptor distances. In the present work, the proton potentials were obtained for structures generated by averaging the reduced and oxidized structures calculated from geometry optimizations with a constrained Ni-N distance. Average structures were obtained for Ni-N distances of 2.94, 3.04, 3.14, and 3.25 Å. The proton potentials were generated on a one-dimensional grid connecting the optimized hydrogen position for the reduced and oxidized states for each Ni-N distance, as depicted at the top of Fig. 3. The rate constants,  and
and 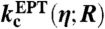 , were calculated at these four Ni-N distances, and a linear interpolation and extrapolation scheme was used to enable the numerical integration over R given in Eq. 5. For the probability functions, we assumed that Pa(R) ≡ Pc(R). The equilibrium distance
, were calculated at these four Ni-N distances, and a linear interpolation and extrapolation scheme was used to enable the numerical integration over R given in Eq. 5. For the probability functions, we assumed that Pa(R) ≡ Pc(R). The equilibrium distance 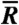 was chosen to be the average of the equilibrium Ni-N distances for the optimized reduced and oxidized complexes, and the effective force constant keff was chosen to be the average of the effective force constants determined by projecting the normal mode vectors onto the proton donor-acceptor axis for the optimized reduced and oxidized complexes (27). These parameters were determined to be
was chosen to be the average of the equilibrium Ni-N distances for the optimized reduced and oxidized complexes, and the effective force constant keff was chosen to be the average of the effective force constants determined by projecting the normal mode vectors onto the proton donor-acceptor axis for the optimized reduced and oxidized complexes (27). These parameters were determined to be 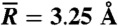 and keff = 0.023495 a.u..
and keff = 0.023495 a.u..
We also explored an alternative approach, in which the proton potentials are obtained for both the reduced and oxidized state structures, and the probability functions for the anodic and cathodic processes are different (i.e., they are determined from the equilibrium Ni-N distance and effective frequency for the optimized reduced and oxidized complex, respectively). Thus, the anodic and cathodic rate constants are calculated with different sets of proton potentials and probability functions. The results of this alternative approach are provided in the SI Appendix. The two approaches give qualitatively similar Tafel plots, as indicated by a comparison of Fig. 5 to the corresponding figure in the SI Appendix, Fig. S5.
The geometry optimizations and proton potentials were calculated with density functional theory and the B3P86 density functional (29, 30) using Gaussian 09 (31). Further computational details about generating the structures and proton potentials are provided in the SI Appendix.
Supplementary Material
Acknowledgments.
We are grateful to Michel Dupuis, Dan DuBois, Morris Bullock, Jim Mayer, Tom Mallouk, and Ben Auer for helpful discussions. This research was supported as part of the Center for Molecular Electrocatalysis, an Energy Frontier Research Center funded by the Department of Energy, Office of Science, Office of Basic Energy Sciences.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1118333109/-/DCSupplemental.
References
-
1.Wiedner ES, et al. Comparison of cobalt and nickel complexes with sterically demanding cyclic diphosphine ligands: electrocatalytic H2 production by
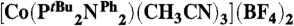 . Organometallics. 2010;29:5390–5401. [Google Scholar]
. Organometallics. 2010;29:5390–5401. [Google Scholar] - 2.Ralph TR, Hogarth MP. Catalysis for low temperature fuel cells. Platinum Metals Review. 2002;46:117–135. [Google Scholar]
- 3.Rakowski DuBois M, DuBois DL. The role of pendant bases in molecular catalysts for H2 oxidation and production. Comptes Rendus Chimie. 2008;11:805–817. [Google Scholar]
- 4.Rakowski DuBois M, DuBois DL. The roles of the first and second coordination spheres in the design of molecular catalysts for H2 production and oxidation. Chem Soc Rev. 2009;38:62–72. doi: 10.1039/b801197b. [DOI] [PubMed] [Google Scholar]
- 5.Yang JY, Bullock RM, Rakowski DuBois M, DuBois DL. Fast and efficient molecular electrocatalysts for H2 production: using hydrogenase enzymes as guides. MRS Bull. 2011;36:39–47. [Google Scholar]
- 6.Frey M. Hydrogenases: hydrogen-activating enzymes. ChemBioChem. 2002;3:153–160. doi: 10.1002/1439-7633(20020301)3:2/3<153::AID-CBIC153>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 7.Fontecilla-Camps JC, Volbeda A, Cavazza C, Nicolet Y. Structure/function relationships of [NiFe]- and [FeFe]-hydrogenases. Chem Rev. 2007;107:4273–4303. doi: 10.1021/cr050195z. [DOI] [PubMed] [Google Scholar]
- 8.DuBois DL, Bullock RM. Molecular electrocatalysts for the oxidation of hydrogen and the production of hydrogen—the role of pendant amines as proton relays. Eur J Inorg Chem. 2011:1017–1027. [Google Scholar]
- 9.Helm ML, et al. A synthetic nickel electrocatalyst with a turnover frequency above 100,000 s-1 for H2 production. Science. 2011;333:863–866. doi: 10.1126/science.1205864. [DOI] [PubMed] [Google Scholar]
-
10.Kilgore UJ, et al. Studies of a series of
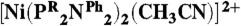 complexes as electrocatalysts for H2 production: substituent variation at the phosphorus atom of the P2N2 ligand. Inorg Chem. 2011;50:10908–10918. doi: 10.1021/ic201461a. [DOI] [PubMed] [Google Scholar]
complexes as electrocatalysts for H2 production: substituent variation at the phosphorus atom of the P2N2 ligand. Inorg Chem. 2011;50:10908–10918. doi: 10.1021/ic201461a. [DOI] [PubMed] [Google Scholar] - 11.Chen S, et al. Comprehensive thermodynamics of nickel hydride bis(diphosphine) complexes: a predictive model through computations. Organometallics. 2011;30:6108–6118. [Google Scholar]
- 12.Cukier RI, Nocera DG. Proton-coupled electron transfer. Annu Rev Phys Chem. 1998;49:337–369. doi: 10.1146/annurev.physchem.49.1.337. [DOI] [PubMed] [Google Scholar]
- 13.Soudackov A, Hammes-Schiffer S. Multistate continuum theory for multiple charge transfer reactions in solution. J Chem Phys. 1999;111:4672–4687. [Google Scholar]
- 14.Hammes-Schiffer S, Soudackov AV. Proton-coupled electron transfer in solution, proteins, and electrochemistry. J Phys Chem B. 2008;112:14108–14123. doi: 10.1021/jp805876e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mayer JM. Proton-coupled electron transfer: a reaction chemist’s view. Annu Rev Phys Chem. 2004;55:363–390. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- 16.Huynh MH, Meyer TJ. Proton-coupled electron transfer. Chem Rev. 2007;107:5004–5064. doi: 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Irebo T, Reece SY, Sjödin M, Nocera DG, Hammarström L. Proton-coupled electron transfer of tyrosine oxidation: buffer dependence and parallel mechanisms. J Am Chem Soc. 2007;129:15462–15464. doi: 10.1021/ja073012u. [DOI] [PubMed] [Google Scholar]
- 18.Costentin C, Robert M, Savéant J-M. Electrochemical concerted proton and electron transfers. Potential-dependent rate constant, reorganization factors, proton tunneling and isotope effects. J Electroanal Chem. 2006;588:197–206. [Google Scholar]
- 19.Costentin C. Electrochemical approach to the mechanistic study of proton-coupled electron transfer. Chem Rev. 2008;108:2145–2179. doi: 10.1021/cr068065t. [DOI] [PubMed] [Google Scholar]
- 20.Fernandez LE, Horvath S, Hammes-Schiffer S. Theoretical analysis of the sequential proton-coupled electron transfer mechanisms for H2 oxidation and production pathways catalyzed by nickel molecular electrocatalysts. J Phys Chem C. 2012;116:3171–3180. [Google Scholar]
- 21.Marcus RA. Chemical and electrochemical electron-transfer theory. Annu Rev Phys Chem. 1964;15:155–196. [Google Scholar]
- 22.Venkataraman C, Soudackov AV, Hammes-Schiffer S. Theoretical formulation of nonadiabatic electrochemical proton-coupled electron transfer at metal-solution interfaces. J Phys Chem C. 2008;112:12386–12397. [Google Scholar]
- 23.Navrotskaya I, Soudackov AV, Hammes-Schiffer S. Model system-bath Hamiltonian and nonadiabatic rate constants for proton-coupled electron transfer at electrode-solution interfaces. J Chem Phys. 2008;128:244712. doi: 10.1063/1.2940203. [DOI] [PubMed] [Google Scholar]
- 24.Ludlow MK, Soudackov AV, Hammes-Schiffer S. Electrochemical proton-coupled electron transfer of an osmium aquo complex: theoretical analysis of asymmetric Tafel plots and transfer coefficients. J Am Chem Soc. 2010;132:1234–1235. doi: 10.1021/ja910277p. [DOI] [PubMed] [Google Scholar]
- 25.Hammes-Schiffer S, Hatcher E, Ishikita H, Skone JH, Soudackov AV. Theoretical studies of proton-coupled electron transfer: models and concepts relevant to bioenergetics. Coord Chem Rev. 2008;252:384–394. doi: 10.1016/j.ccr.2007.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Edwards SJ, Soudackov AV, Hammes-Schiffer S. Analysis of kinetic isotope effects for proton-coupled electron transfer reactions. J Phys Chem A. 2009;113:2117–2126. doi: 10.1021/jp809122y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Auer B, Fernandez LE, Hammes-Schiffer S. Theoretical analysis of proton relays in electrochemical proton-coupled electron transfer. J Am Chem Soc. 2011;133:8282–8292. doi: 10.1021/ja201560v. [DOI] [PubMed] [Google Scholar]
- 28.Liu Y-P, Newton MD. Reorganization energy for electron transfer at film-modified electrode surfaces: a dielectric continuum model. J Phys Chem. 1994;98:7162–7169. [Google Scholar]
- 29.Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 30.Perdew JP. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys Rev B. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- 31.Frisch MJ. 2010. Gaussian 09, Revision B.01. (Gaussian, Inc., Wallingford, CT)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.