Are ParM Filaments Polar or Bipolar?

Abstract

A recent Perspective (J. Mol. Biol., in press) by Harold Erickson has suggested that published reconstructions of bacterial ParM filaments from three different laboratories may have artifactually imposed polarity upon a filament that is really bipolar, with the two strands running in opposite directions. We show that Erickson’s model of a bipolar filament can be easily distinguished from a polar filament by helical diffraction, since the asymmetric unit in a bipolar filament would be twice the size as in a polar filament. Existing data from both electron cryo-microscopy and x-ray diffraction exclude a bipolar model. We adopt the suggestion put forward by Erickson to process filaments assuming that they are bipolar, and show that the resulting filaments are polar.

Erickson has advanced the interesting hypothesis¹ that our reconstructions of ParM^{2, 3}, and those from other laboratories^{4, 5}, are artifacts, and that the actual ParM filament is not polar, but consists of two strands with opposite polarities. We would like to correct some factual errors in Erickson’s paper about our work because these bear on how that work relates to Erickson’s suggestion of bipolarity. We used electron cryo-microscopy, and not negative stain as he stated, and the resolution of our reconstruction was ~ 1.7 nm, and not 2.3 nm (a difference of ~ 2.5 in information content). But even at 3.0 nm resolution the polarity of ParM filaments is clear, and existing data can distinguish between a polar and bipolar filament. This short note is therefore of more general interest if it helps to illuminate topics that may seem arcane. In applying the Iterative Real Space Helical Reconstruction (IHRSR) algorithm⁶ we did not “impose” polarity upon a structure that is really bipolar. Rather, we imposed a helical symmetry that was evident from power spectra of filaments. This symmetry corresponds to an axial rise of ~ 2.5 nm per subunit, and a rotation of 165° between subunits. This symmetry generates two strands that are symmetrical and of the same polarity. Erickson’s bipolar model must mean that the symmetry in the filament would be an axial rise of ~ 5.0 nm, and a rotation of −30°, which would be the result of the asymmetric unit in the filament being a dimer of ParM molecules, with one pointing up and the other pointing down. Models and power spectra in Fig. 1 show how easily distinguishable these two helical symmetries are, and how the actual power spectra from cryo-EM images match the polar model, and not a bipolar one. In fact, x-ray fiber diffraction patterns⁵ from ParM filaments extend beyond 8 Å and clearly show that the helical symmetry is incompatible with Erickson’s model (where the asymmetric unit is a dimer). There would be no ambiguities in distinguishing between these different symmetries. Erickson’s model would predict that the meridional intensities in such a pattern would fall on multiples of 1/(5.0 nm), and not at multiples of 1/(2.5 nm) as observed.

Figure 1.

(a,b) Two models are shown for the ParM filament. In (a), (PDB ID 3IKU) the asymmetric unit is a single ParM subunit, shown in red. One strand is in orange, and the other strand is in cyan, and both strands have the same polarity. In (b), the type of model proposed by Erickson, one strand has the opposite polarity as the other strand, and the asymmetric unit in such a polymer must be a dimer of ParM, shown in red. Of course, there are an infinite number of different bipolar models that one might generate, but all have the property that the asymmetric unit is a dimer. The model that we show in (b) has a stagger of the two strands such that the centers of mass of each subunit are approximately the same as in (a). The two models shown generate very different power spectra (c and d, respectively, right sides) which can be compared with the real power spectrum (c and d, left side) obtained from frozen-hydrated unstained ParM filaments². The power spectrum from a polar model of ParM (c) matches the observed power spectrum quite well, and the first meridional intensity from the model occurs at 1/(2.5 nm). The power spectrum from a bipolar model of ParM (d), due to the asymmetric unit being twice the size, generates features that are completely absent in the observed power spectrum. Because the two strands are staggered, there is no meridional intensity from the model in (d) at 1/(5 nm), the reciprocal of the rise per dimer. The first meridional intensity in this particular model occurs at 1/(1.67 nm), the third order of 1/(5 nm). The difference in relative intensities between the real power spectrum and the model (c) is due to the fact that the images have been multiplied by a contrast transfer function twice: once by the microscope, and once by us in correcting the phases and improving the signal to noise ratio. The striking difference in the power spectra of the two models is that the spacing between the layer lines (red arrows) in the polar model (c) is ~ 1/(30 nm), while in the bipolar model (d) the spacing (blue arrows) is half this distance, ~ 1/(60 nm).

A misunderstanding on Erickson’s part is that the reconstruction algorithm might somehow impose a polarity when one does not exist. The same algorithm and approach that we used to solve ParM was used on ICP8 and ParA2 filaments^{7, 8}, and both of those filaments were revealed to be bipolar. This never required an initial assumption that they were bipolar or polar, rather, the bipolarity was shown by the reconstruction. In all cases, reconstructions begin with a solid cylinder as an initial reference, eliminating the possibility that the features that emerge are biased by initial assumptions. So Erickson’s argument that the “existing EM reconstructions imposed an assumption of polarity, rather than discovering it” is wrong.

Let us now ignore the issue of the power spectra and ask what would happen if Erickson was correct, and we had averaged together subunits pointing up on one strand with subunits pointing down on the opposite strand. The result would be two identical strands, but the subunits on each strand would be bipolar, a consequence of the artifactual averaging. What we saw instead² were polar subunits that provided an excellent fit to the crystal structures⁴ of ParM. At 17 Å resolution there was no ambiguity in fitting a ParM crystal structure into our reconstruction, while we would hardly expect this to be the case if the entire reconstruction was artifactual with the wrong symmetry⁹.

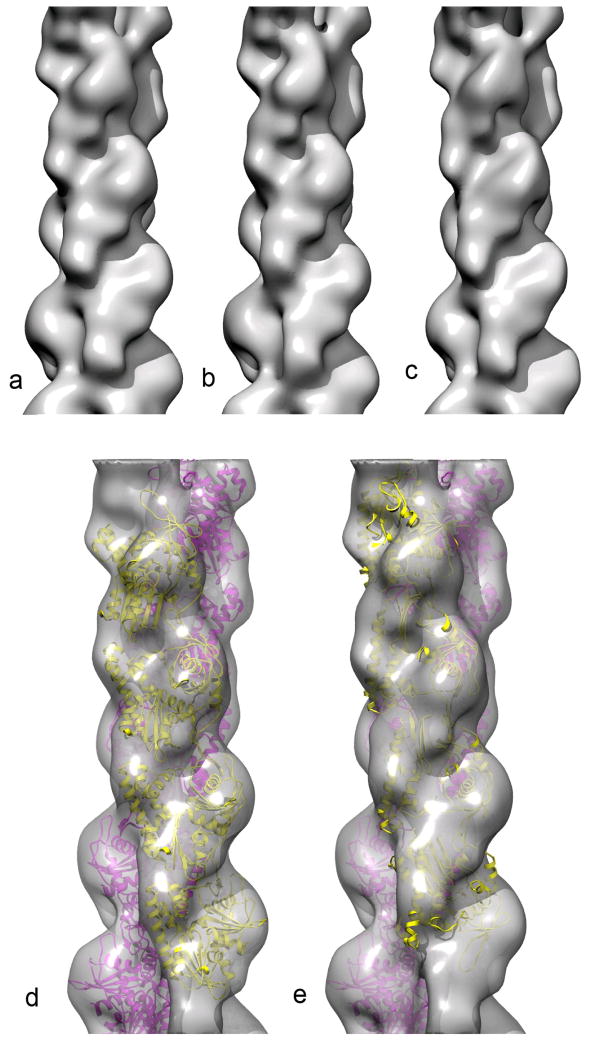
Nevertheless, we have actually done what was proposed by Erickson¹: “One might suggest repeating the EM reconstruction with an assumption of antiparallel symmetry, both in the initial model and in the final fitting.” As explained above, we started with an assumption of an axial rise of 5.0 nm and a rotation of −30° per dimer. Assuming bipolar strands in our algorithm is not the same as imposing it on the reconstruction. If the filament is really polar, one expects a polar reconstruction with the two strands being only slightly different since they are not averaged together. If the filament is really bipolar, then one should get two strands that look approximately the same but one is upside down relative to the other. We used 3,611 segments, each 200 pixels long, with 2.38 Å/px. The IHRSR algorithm converged to a symmetry of 4.92 nm and a rotation of −29.0°. The reconstruction (Fig. 2b,c) looks extremely similar to that previously published² from these same segments (Fig. 2a). To test this in the molecular fitting, we used the software package Chimera¹⁰ which provides a “fit to map” function. The coefficient of correlation between the atomic model of ParM (filtered to 17 Å resolution) and the new map was 0.775 for both chains parallel, but 0.497 for the chains being anti-parallel. Looking at a single chain, the coefficient of correlation was 0.8165 when it was in the same orientation as the opposite strand (Fig. 2d), but only 0.3668 when it was antiparallel to the opposite strand (Fig. 2e).

Figure 2.

Our original reconstruction² of ParM in the closed state (a) can be compared with a reconstruction where the asymmetric unit is taken as a dimer, with one protomer from each strand (b,c). The volume in (c) has been rotated by 165.5° and shifted axially by 2.46 nm with respect to the volume in (b), so that the opposite strand is shown. It can be seen that both strands are very similar, and have the same orientation. The volume reconstructed with the asymmetric unit being a dimer can be fit with the atomic model for the ParM filament (PDB 3IKU) in (d). One strand of this model is then flipped in polarity, and the best fit is shown (e), which is clearly much worse than the fit in (d).

The motivation for Erickson’s model appears, in part, to be the observation that ParM filaments elongate with equal rates at both ends¹¹. While Erickson states that “there is no thermodynamic requirement” for two different rates, he finds this unusual. Actually, in the absence of a conformational change of the subunit, kinetics and thermodynamics tells us that the rates of addition and loss at the two ends of a polar polymer must be identical, since every salt bridge or ionic bond formed, and water molecule displaced, at one end must happen at the other end. It is a conformational change of the subunit associated with polymerization that breaks this symmetry in rates at the two ends. We now have insights into the conformational change associated with actin polymerization¹², and what ParM polymerization kinetics tells us is that such a change does not take place in ParM.

• A model has been proposed for a bipolar ParM filament

• The asymmetric unit in such a filament would be a dimer

• We show that this model is inconsistent with diffraction from x-ray and EM

• We process ParM images assuming a dimer, and show that filament is polar