Motion Parallax from Microscopic Head Movements during Visual Fixation

Abstract

Under normal viewing conditions, adjustments in body posture and involuntary head movements continually shift the eyes in space. Like all translations, these movements may yield depth information in the form of motion parallax, the differential motion on the retina of objects at different distances from the observer. However, studies on depth perception rarely consider the possible contribution of this cue, as the resulting changes in viewpoint appear too small to be of perceptual significance. Here, we quantified the parallax present during fixation in normally standing observers. We measured the trajectories followed by the eyes in space by means of a high-resolution head-tracking system and used an optical model of the eye to reconstruct the stimulus on the observer’s retina. We show that, within several meters from the observer, relatively small changes in depth yield changes in the velocity of the retinal stimulus that are well above perceivable thresholds. Furthermore, relative velocities are little influenced by fixation distance, target eccentricity, and the precise oculomotor strategy followed by the observer to maintain fixation. These results demonstrate that the parallax available during normal head-free fixation is a reliable source of depth information, which the visual system may use in a variety of tasks.

1. Introduction

Even when we attempt to maintain steady gaze on a single point, the images on our retinas are never stationary. This physiological motion of the input stimulus is commonly studied with the head immobilized, a procedure necessary to measure microscopic eye movements, such as microsaccades and ocular drift (Ratliff and Riggs, 1950; Ditchburn, 1973; Steinman et al., 1973). When the head is not restrained, however, fixational eye movements do not occur in isolation, but are accompanied by continual adjustments in body posture and small reorientations of the head (Skavenski et al., 1979; Ferman et al., 1987; Demer and Viirre, 1996; Crane and Demer, 1997). These movements, which in this study we collectively group under the term “fixational head movements”, possess translational and rotational velocities that exceed 1 cm/s and 1 deg/s, respectively, and contribute to the normal motion of the retinal stimulus (Steinman et al., 1982; Steinman, 2003).

Do fixational head movements serve visual functions? Although it is certainly possible that these incessant changes in viewpoint are simply an involuntary outcome of the motor strategy by which humans maintain balance and fixation, the visual system could still benefit in multiple ways from the resulting spatiotemporal modulations in the input signals. A possible beneficial impact of this motion is improved visibility. It is a long-standing hypothesis that the fixational motion of the retinal image is necessary to refresh neural activity and prevent the perceptual fading that is otherwise experienced when stimuli are kept stationary on the retina (Riggs et al., 1953). Although studies of image fading have focused almost exclusively on microsaccades (Rolfs, 2009)— the most accessible component of fixational instability—, it has long been observed that the high retinal velocities present during normal head-free fixation should be sufficient for optimal visibility (Skavenski et al., 1979; Collewijn and Kowler, 2008).

Furthermore, fixational head movements could also participate in the encoding of visual information, as suggested by models of neurons in the early visual system (Rucci, 2008). When the head is immobilized, microscopic eye movements enhance vision of high-frequency patterns (Rucci et al., 2007), a phenomenon that appears to originate from a temporal equalization of the spatial power of the stimulus on the retina (Kuang et al., 2012). Under more natural conditions, both head and eye movements cooperate to yield a specific amount of retinal image motion (Collewijn et al., 1981), and fixational head movements may therefore contribute to this spatiotemporal reformatting of visual input signals.

While the previous two hypotheses attribute similar functions to fixational eye and head movements, there is a more specific way in which the visual system could benefit from the retinal image motion resulting from head/body instability. Unlike the almost pure rotations occurring during eye movements (but see Hadani et al., 1980 and Bingham, 1993), fixational head movements translate the eyes in space. As any translational movement, this change in viewpoint does not merely shift the image on the retina, but causes relative motion between the retinal projections of objects at different distances from the observer. Thus, fixational head movements could, in principle, also provide depth information in the form of motion parallax.

Motion parallax is a powerful 3D cue, which is usually studied within the context of much larger movements of the observer (Rogers and Graham, 1979; Rogers, 2009). The small translations resulting from fixational head movements may, at first sight, appear insufficient to yield useful parallax. Several findings, however, indicate that this intuitive assumption may be inaccurate. The results of a recent study, in which subjects grasped and placed objects while standing, suggest that motion parallax resulting from small head movements contributed to the evaluation of the slant of a surface (Louw et al., 2007). Furthermore, the observation that the posture of standing subjects is influenced by relative motion in the scene indicates that the parallax resulting from body sway is used in the control of posture (Bronstein and Buckwell, 1997; Guerraz et al., 2000, 2001).

Although the previous findings support the notion that the visual system uses the motion parallax resulting from fixational head movements, studies of depth perception rarely consider this cue. This occurs in part because the actual parallax caused by fixational head movements has never been quantified, and the default assumption is that relative velocities are too low to be used reliably in depth judgments. The present study is designed to fill this gap. We have recorded the head translations and rotations of standing observers during fixation and reconstructed the spatiotemporal stimuli on their retinas. This approach allows quantitative analysis of the parallax experienced by the observer. Our results demonstrate that, for objects within a few meters from the observer, the relative velocities resulting from normal fixational head movements are well above perceivable threshold levels.

2. Methods

2.1. Subjects

Three observers (ages: 29, 31, and 37) with normal or corrected-to-normal vision participated in the experiments. Two subjects were naive about the purpose of the study. The third one (MA) was one of the authors. Informed consent was obtained from all subjects in accordance with the procedures approved by the Boston University Charles River Campus Institutional Review Board.

2.2. Apparatus

Head movements were measured by means of an optical motion-capture system with four cameras (Phasespace, Inc). Each camera covered a visual angle of 60° and contained two linear detectors, which provided a resolution equivalent to 3600 × 3600 pixels. The cameras were positioned at the four upper corners of a cubic workspace (side length: 2.2 m) and were oriented so that their lines of sight intersected at the center of a horizontal cross-section 180 cm above the floor. Subjects wore a tightly-fitting helmet equipped with 20 active LED markers, each one modulated at its own frequency. Images of the markers were acquired at a frequency of 480 Hz and converted into estimates of their 3D positions with a resolution of approximately 0.5 mm. This conversion was based on an initial calibration, during which 8 LED markers in a known collinear arrangement were positioned at various locations within the working area. The markers’ positions recorded during the experiments were then used off-line, after completion of the recording session, to estimate the 3D position and orientation of the head.

2.3. Procedure

Head movements were recorded while observers maintained fixation on a 13′ high-contrast cross in a normally illuminated room (Fig. 1a). The fixation marker was presented at eye level, in front of the subject, at six different distances on the anterior-posterior (Z) axis. Adjacent distances were separated by 50 cm increments within the 50-300 cm range. Subjects stood comfortably on a carpeted floor with their feet at about shoulder-length apart and were instructed to maintain accurate fixation and remain as immobile as possible. Each trial lasted 17.5 s and started with the subject pressing a button on a keyboard. Following the button press, the subject had 5 s to assume a stable posture and fixate on the cross before the recording started. The head position was then recorded for a period of 12.5 s, until a tone indicated the end of the trial. Fifteen trials were collected for each distance of the fixation marker, with breaks in between trials to prevent fatigue. This yielded a total of 1,125 s of recording time for each subject.

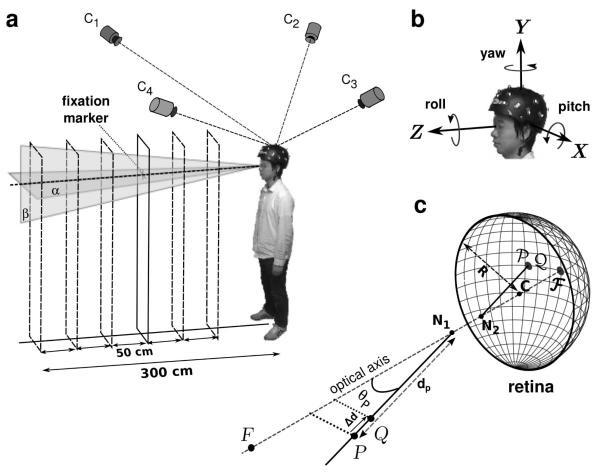
Fig. 1.

Experimental procedure. (a) Subjects maintained fixation on a small cue, at variable distance, while wearing a tightly-fitting helmet equipped with 20 active LED markers. A motion capture system with 4 high-speed cameras (C₁ - C₂) estimated the position of the markers in space. (b) These data were used to estimate the Cartesian coordinates (x, y, z) and orientation (yaw, pitch, roll) of the helmet. (c) Retinal image motion was estimated by means of Gullstrand’s schematic eye model. The radius of the model eye (R) was 11.75 mm. The distances of the first and second nodal point (N₁ and N₂) to the center of rotation (C) were 5.7 mm and 5.4 mm, respectively. F represents the fixation point and $\mathcal{F}$ its projection on the retina. P and Q are two point light sources with coincident retinal projections (P and Q) used to estimate parallax thresholds.

2.4. Estimation of head movements

Instantaneous head rotations and translations were estimated at 480 Hz based on the recorded coordinates of the LED markers. In a calibration session prior to the experiments, a 3D rigid-body model of the helmet was developed by placing the helmet on a manikin head at the center of the workspace. In this position, it was possible to measure the location of each LED marker very accurately, so that, for all the 20 markers, the standard deviations of their recorded Cartesian positions were all smaller than 0.1 mm. These data enabled precise determination of the position of each LED relative to the center of mass of the ensemble.

The head position was estimated by computing the sequence of rigid body transformations that best interpolated, according to least-squares, the recorded marker traces (Horn, 1987). For each recorded sample, this algorithm generated a translation vector and a quaternion. These two elements, together, fully described the head’s position and orientation in a world-centered frame of reference with origin at the helmet’s mean centroid position. This coordinate system was oriented as illustrated in Fig. 1b, with the Z axis pointing toward the fixation target and the Y axis orthogonal to the floor. Thus, apart from possible small offsets that may have occurred because the subject did not perfectly align the body to face the target, the Z and X axes coincided with the anterior-posterior and mediolateral axes, respectively. Quaternions were successively converted into yaw, pitch and roll angles following Fick’s convention as shown in Fig. 1b (Haslwanter, 1995). This approach gave three translational (x, y, and z) and three rotational (yaw, pitch, and roll) variables.

The precision of head-tracking was assessed by finely controlling the helmet’s position by means of a robotic manipulator (Directed Perception Inc). These tests have shown that the adopted approach gives very high spatial resolution. The 90th percentile of the estimation error for translations was 0.47 mm. Rotations around yaw and pitch axes gave measurement errors with 90th percentiles equal to 0.3′ and 0.4′, respectively. Thus, this system is capable of resolving the small head movements that occur during visual fixation.

2.5. Estimation of retinal image motion

Retinal image motion was estimated by means of Gullstrand’s schematic eye model with accommodation (von Helmholtz, 1924; see Fig. 1c). For simplicity, this model assumes that the vertical and horizontal axes of rotation intersect at the center of the eye and that visual and geometric axes coincide. A preliminary calibration procedure was conducted to locate the center of rotation of both eyes relative to the helmet. This operation was accomplished by placing an LED marker on each of the observer’s eyelids and recording their positions. The coordinates of the rotation centers were assumed to lie 25.5 mm behind the markers, a displacement given by the sum of the marker’s thickness and the distance between the surface of the cornea and the center of rotation, which in Gullstrand’s eye model is estimated at 13.5 mm.

Having estimated the trajectory followed by the eye in space, we reconstructed the retinal image that would be given by a point light source, P, at a given spatial location and measured the position of its retinal projection $\mathcal{P}$ at each time step of the recordings. As illustrated in Fig. 1c, the vector $\overline{C\mathcal{P}}$ which identifies the position P on the retina was computed as the sum of $\overline{{\mathit{CN}}_2}$, the vector connecting C to the second nodal point, and $\overline{N_2\mathcal{P}}$, the vector connecting N₂ to the retinal projection P. This latter vector is given by:

$$\overline{N_2\mathcal{P}}=\Vert N_2-\mathcal{P}\Vert \mathrm{u}=\left(\Vert C-N_2\Vert \cos \left({\theta }_P\right)+\sqrt{R^2-\Vert C-N_2{\Vert }^2{\sin }^2\left({\theta }_P\right)}\right)\mathrm{u}$$ (1)

where R is the radius of the eye, and $\mathrm{u}=\frac{\overline{{\mathit{PN}}_1}}{\Vert \overline{{\mathit{PN}}_1}\Vert }$ is the unit vector with direction identical to $\overline{{\mathit{PN}}_1}$

The retinal projection P was then expressed in an eye-centered coordinate system with origin at the eye’s center of rotation C. Its velocity vector, which is tangential to the retinal surface, is given by ${\mathrm{v}}_{\mathcal{P}}\left(t\right)=\frac{d\overline{C\mathcal{P}}}{\mathit{dt}}$. The corresponding instantaneous angular speed on the retina is $\frac{1}{R}\Vert {\mathrm{v}}_{\mathcal{P}}\left(t\right)\Vert$.

Retinal image motion was estimated for point sources positioned at evenly spaced locations on the horizontal plane α and on the vertical plane β (see Fig. 1a). The horizontal plane α was the plane parallel to the floor at the observer’s average eye level. The vertical plane β was the plane orthogonal to α at the mean y position of the head. Since results obtained for the two eyes were very similar, only data for the left eye are reported here.

2.6. Estimation of parallax

To quantify motion parallax, we examined the differential motion between the retinal projections of pairs of simulated point light sources resulting from the head movements recorded in the experiments. The locations of these simulated targets were systematically varied in the simulations. Pairs of points projecting onto the same retinal location were directly compared by calculating the modulus of the difference between their velocity vectors.

To summarize the depth resolution provided by motion parallax, at each considered spatial location, we estimated the depth of the region of uncertainty, the region within which retinal velocity remained below a chosen threshold. Fig. 1c describes the procedure. Given a stimulus P, we determined the minimal change in depth that would yield a difference in its mean instantaneous velocity on the retina larger than 1’/s (Δd in Fig. 1c). This velocity value was selected as a conservative detection threshold for differential velocity based on the results of previous studies on parallax and motion perception (Nakayama and Tyler, 1981; Ujike and Ono, 2001; Shioiri et al., 2002). In practice, as shown in Fig. 1c, depth thresholds were estimated by placing a second point light source Q at the same position of P and by moving it closer to the observer on the projection axis $\overline{{\mathit{PN}}_1}$ until the difference between its velocity on the retina, v_Q, and the velocity of P, v_P, exceeded 1’/s. The amplitudes of these two velocity vectors could be easily compared, as the two points projected at the same retinal location, and the two vectors were parallel to each other. The resulting separation Δd can be regarded as a prediction about the minimum depth detectable at the considered spatial location on the basis of fixational parallax. In the following of this paper, we refer to Δd as the expected (or predicted) depth threshold.

During head movements, the eyes rotate in their orbits in order to maintain fixation. Since eye movements were not recorded in the experiments, unless otherwise indicated, we assumed that eye movements perfectly compensated for head movements. That is, in the reconstruction of the retinal stimulus, the model eye rotated so to maintain the point of fixation immobile in the retinal image. We analyzed the impact of different oculomotor strategies by means of computer simulations, in which the eye rotations needed for perfect fixation were scaled by a compensation gain between 0 and 1 (0 no compensation; 1 full compensation).

3. Results

In agreement with previous reports (Paulus et al., 1984; Skavenski et al., 1979; Crane and Demer, 1997), normally standing observers moved significantly while maintaining fixation. Fig. 2 shows an example of the head trajectories recorded in our experiments. In this trial, the head gradually translated backwards by almost 4 cm on the Z axis, while oscillating by approximately 1 cm on the X axis and by a smaller amount along the Y axis (Fig. 2a). As the subject moved backwards on the Z axis, he also performed a pitch rotation of approximately 4°, which presumably resulted from the head moving with the body without compensating for the translation (Fig. 2b). Oscillatory yaw rotations, which appeared to compensate for the translational movements on the mediolateral axis, and smaller roll rotations were also visible. All these movements occurred even though observers were explicitly instructed to remain as immobile as possible while maintaining fixation.

Fig. 2.

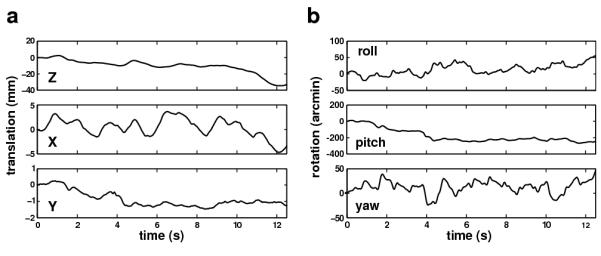
An example of recorded head movements in a typical experimental trial. The observer maintained fixation on a target at 1 m distance. Each graph represents the change in position along one of the six degrees of freedom. Both (a) translations and (b) rotations are shown.

As a first step toward estimating the parallax experienced by the observers, we examined the characteristics of fixational head movements. Fig. 3a reports the 75% and 95% confidence intervals of the probability distributions of head movement along each degree of freedom for the three observers who took part in the study. For each observer, these distributions were based on data recorded at 480 Hz for a period of 1,125 s. These data show that while the amplitude of instability varied with each individual observer—a well established fact in the posture control literature (Black et al., 1982)—the general characteristics of fixational head movements were similar across observers. Translations were most pronounced along the anterior-posterior (Z) axis, on which all three subjects moved by more than 15 mm. Significant translations also occurred on the X axis, with an average 95th percentile of 8 mm. In contrast, motion was minimal on the vertical (Y) axis, as it should be expected given that observers stood still with both feet on the ground. Head rotations were also considerable, with 95th percentiles ranging from approximately 0.5° to more than 3°. Two subjects (MB and MA) performed primarily pitch rotations, with ranges that were almost the double of those of yaw and roll rotations. Subject XK exhibited more even distributions around the three rotation axes, with a slight preference for yaw rotations.

Fig. 3.

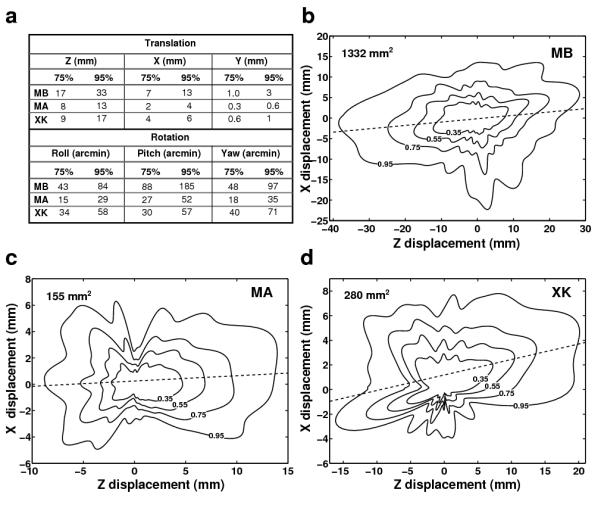
Characteristics of fixational head movements. (a) 75% and 95% confidence intervals of head translations and rotations along each degree of freedom. Different rows report data from different observers. (b-d) Probability distributions of head displacement on the horizontal plane. Contours represent confidence regions with different probabilities. Dashed lines represent the axes with maximum dispersion which deviated slightly from the Z axis. Data from different subjects are shown in different panels. The numbers in each panel represent the 95% confidence areas.

Because the head moved little along the Y axis, translational movements were well described by the probability density functions of the head position on the horizontal (XZ) plane. These functions are shown for each observer in Fig. 3b-d. Given that no systematic differences were visible in the head trajectories recorded during fixation on targets at different distances, these probabilities were estimated over all the available trials for each individual subject. To better illustrate the movement, trials were aligned by their starting position (the origin of each graph).

Thus, the value at a given point in each map represents the probability that the head translated on the anterior-posterior and mediolateral axes by the amounts corresponding to the point’s z and x coordinates. These data show that all three observers moved considerably while maintaining fixation. In all observers, small deviations between the axis with the highest dispersion of head position and the Z axis were also visible. Measured angular offsets were 4.7° for subject MB, 2.3° for subject MA, and 7.2° for subject XK. These offsets could have been caused by biases in the maintenance of body balance and/or small postural misalignments during the recordings (the subject did not perfectly align the body to face the target).

Together, head translations and rotations determine how the eyes move in space. As explained in the Methods, before starting each recording session, we performed a preliminary calibration to localize the centers of rotation of both eyes relative to the optical markers. This calibration enabled estimation of the 3D trajectories followed by the eyes in space. Although slightly larger than vertical head movements, eye translations along the vertical (Y) axis were relatively small (average 95th percentile: 2.8 mm), and Fig. 4a shows the distributions of eye displacements on the horizontal plane. The eyes translated by several millimeters during fixation following distributions that were similar to those measured for the head (see Fig. 3). The 95% confidence regions—the regions in which the eye remained 95% of the time— were only slightly smaller than the corresponding regions for head movements, suggesting that head rotations had a relatively small influence on eye translations. Indeed, a regression analysis between head and eye translations in individual trials revealed that head translations accounted for 99% of the variance of eye translation on the Z axis and for 97% of the variance on the X axis.

Fig. 4.

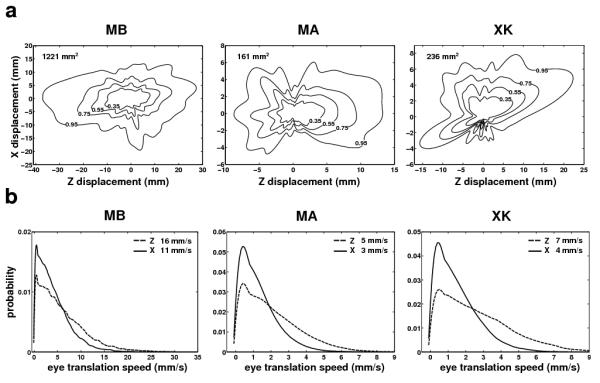
Eye translations caused by fixational head movements. (a) Probability distributions of the eye location on the horizontal plane. (b) Probability density functions of translational speeds on the anterior-posterior (Z) and mediolateral (X) axes. In both a and b, different panels show data from different subjects. Data refer to the trajectories followed by the center of rotation of the left eye. Virtually identical data were obtained for the right eye. Numbers in each panel represent 95th percentiles.

Fig. 4b shows the distributions of the velocity components of eye displacement on the Z and X axes for the three observers. Not surprisingly, the eye moved slightly faster on the Z axis than on the X axis. But velocities of several millimeters per second were observed in both directions. Note that for stationary objects up to 3 m from the observer even a translation of 1 mm/s may provide a useful parallax, as it yields retinal speeds of several arcmins per second. It has been reported that, during head translations slower than a few centimeters per second, perceptual thresholds for motion parallax only depend on relative speed (Ujike and Ono, 2001). These data show that translational velocities measured during normal fixation were well within this range. Thus, the visual consequences of these movements can be evaluated by examining the differential motion they yield in the retinal image.

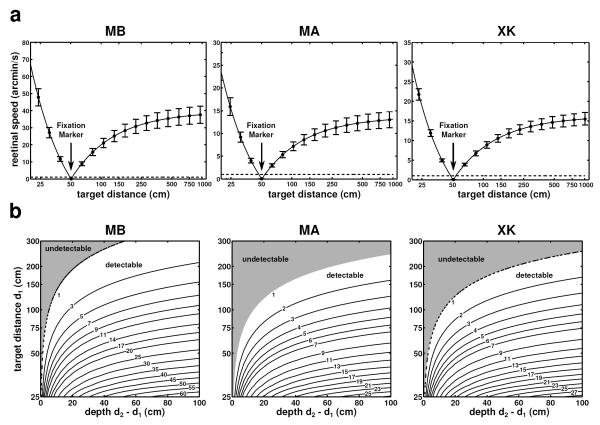
Fig. 5a shows the mean instantaneous retinal speed (the absolute value of the instantaneous velocity vector on the retina) measured for targets positioned at various distances on the Z axis when the fixation marker was located at 50 cm. Even though the head moved by small amounts and at low speed, objects at distances different from the fixation marker moved on the retina with relatively high speed. With the exception of targets located within a very small range of distances around the fixation point, targets at all other distances yielded mean instantaneous speeds sufficiently large to be visible. The extent of the regions around the fixation point for which target speed fell below 1’/s—a value close to the thresholds for differential motion—were only 3 cm for subjects MB, 7 cm for subject MA, and 5 cm for subject XK. Thus, these data show that, during fixation on an object at 50 cm, the retinal speed resulting from fixational head movement may enable discrimination of targets that are only a few centimeters away from the point of fixation.

Fig. 5.

Retinal speed and motion parallax on the zero azimuth axis. (a) Mean instantaneous retinal speed of simulated point sources at different distances from the observer. Subjects maintained fixation on a marker at 50 cm (indicated by the arrow). Vertical bars represent one standard deviation. (b) Parallax between all possible pairs of points within a distance of 4 m from the observer. In each graph, the value at coordinates (x, y) represents the mean difference (in modulus) of the mean instantaneous retinal velocities of two point sources located at distances y and y + x from the observer. In both rows, different columns show data from different observers. Dashed lines in all graphs indicate a speed of 1’/s, taken here as the detection threshold of an average observer.

The data in Fig. 5a can be regarded as the motion parallax of objects at different distances on the Z axis (0° azimuth) relative to the point of fixation, which was assumed to remain stationary on the retina. More in general, Fig. 5b shows the parallax between any pair of points on this axis. A point in each of the maps of Fig. 5b represents the mean modulus of the difference in the instantaneous retinal speeds of two points at distance d₁ and d₂ from the observer (d₁ < d₂). Since all these pairs of points project on the retina at very nearby locations within the fovea, one may expect the visual system to be capable of detecting very small velocity differences. As expected from the geometry of the parallax, speed differences increased monotonically with the depth d₂ – d₁, an increment that became less pronounced as the distance d₁ between the closer point and the observer increased. Yet, most pairs of points within 3 m from the observer yielded mean differences in instantaneous retinal speed above 1’/s (92% of pairs for subject MB, 78% for subject MA, and 80% for subject XK). Thus, the parallax resulting from fixational head movements was significant even in the most stable observer.

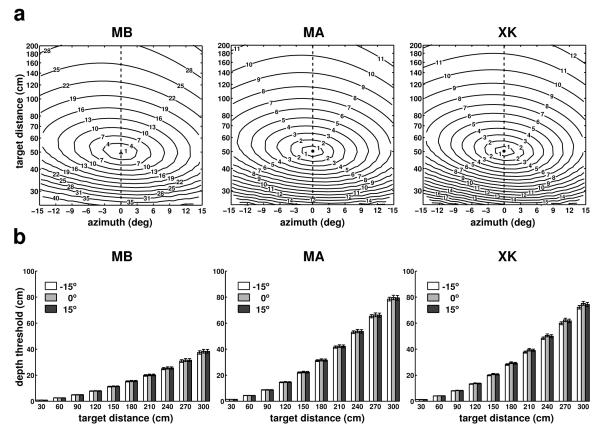
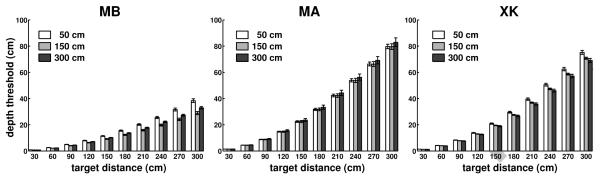
The results in Fig. 5 were obtained for points on the Z axis (0° azimuth). Fig. 6 shows results for targets located in a broader region (±15° azimuth) on the horizontal plane at eye level (plane α in Fig. 1). As before, also in this case the fixation marker was at 50 cm from the observer. Maps of the instantaneous speed of retinal image motion for simulated point sources at various locations in front of the observer are given in Fig. 6a. As shown by these graphs, the speed of the stimulus on the retina increased not only with the distance of the target relative to the fixation point, but also with the target’s eccentricity, yielding a complex motion pattern on the retina. This occurred because as the eccentricity of the target increased, the anterior-posterior component of fixational head movements contributed more significantly to retinal velocities. However, this change in speed had little influence on the actual parallax. Fig. 6b shows that depth thresholds—the minimum depth change necessary to yield a 1’/s change on the retina— were virtually identical for targets located at ±15° and 0° azimuth. These thresholds varied across subjects depending on the amplitude of fixational head movements, but enabled good spatial resolution within nearby space in all three observers. For a target at 1 m, they were only 6 cm for subject MB, 11 cm for subject MA, and 10 cm for subject XK.

Fig. 6.

Characteristics of motion parallax on the horizontal plane at eye level. (a) Mean instantaneous retinal speed given by simulated point sources located within ±15° azimuth and 3 m distance on the horizontal plane at average eye level. (b) Minimum depth displacements resulting in speed differences of 1’/s for targets located at three different azimuth angles: −15°, 0°, and 15°. Errorbars represent standard errors. Different panels show data for different observers.

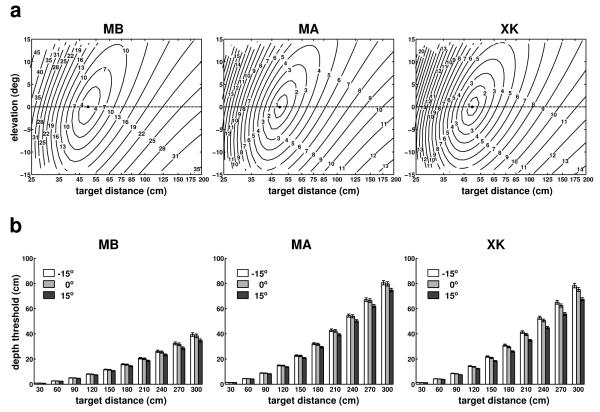
Similar results were also obtained at different elevations. Fig. 7a shows the mean retinal speeds of simulated point light sources at various locations on the vertical plane at 0° azimuth (plane β in Fig. 1). In all subjects, speed distributions were not symmetrical, but increased faster in a direction with average angular offset of 7° relative to the Z axis. This asymmetry was caused by the way the eye moved on the vertical plane, which was similar to an inverted pendulum with correlated z and y components, yielding a stronger effect in the lower portion of the visual field. Depth thresholds were also influenced by this coupling (Fig. 7b) and were slightly lower for targets at −15° elevation than for targets at +15°. However, this modulation was modest, and changes in depth thresholds across the 30° elevation range were only 5 cm, 9 cm, and 11 cm for subjects MB, MA and XK, respectively. These data, together with those in Fig. 6, show that the motion parallax resulting from fixational head movements provides good depth resolution in the space nearby the observer.

Fig. 7.

Characteristics of motion parallax on the vertical plane at 0° azimuth. (a) Mean instantaneous retinal speed given by simulated point sources located within ±15° elevation and up to a distance of 3 m. (b) Minimum depth displacements resulting in speed differences of 1’/s for targets located at three different elevation angles: −15°, 0°, and 15°. Errorbars represent standard errors. Different panels show data for different observers.

The results of Figs. 5-7 were obtained while subjects maintained fixation at a distance of 0.5 m. We also examined the effect of changing the distance of the fixation marker. Since subjects performed head movements with similar characteristics while fixating on markers at different distances, fixation distance may be expected to only have a marginal effect on the parallax. Fig. 8 confirms this expectation; depth thresholds on the zero azimuth axis obtained during fixation on markers at 1.5 m and 3 m were similar to those measured during fixation on a marker at 0.5 m. The minor changes visible in Fig. 8 were primarily caused by differences in the velocities of head movements recorded during fixation at different distances. In subjects MB and XK, these changes led to an improvement in depth resolution. This effect was, however, small, and across the three observers, the depth threshold for a target at 3 m was only 5 cm smaller when the target was fixated than when fixation was maintained on a marker at 0.5 m. Thus, the depth resolution resulting from this cue was little influenced by both the azimuth of the target and the distance of the fixated object.

Fig. 8.

Influence of the fixation distance. Depth thresholds for simulated targets at different locations on the Z axis during fixation on markers at 0.5 m, 1.5 m, and 3 m from the observer. Different panels show data for different observers. Errorbars represent standard errors.

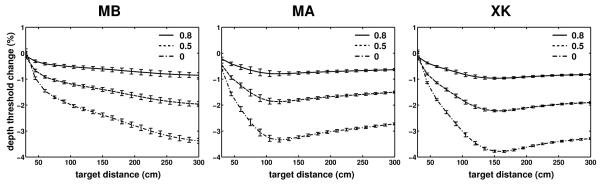
In our experiments, we did not measure eye movements, and the results presented so far are based on the assumption that subjects maintained perfect fixation on the marker. That is, in the simulations that reconstructed retinal image motion, the eyes rotated so as to maintain the fixation point immobile on the fovea. Pure rotations do not cause parallax. However, because in the eye the optical nodal points are not coincident with the center of rotation (see Fig. 1c), small translations of the nodal points do occur during eye movements (Hadani et al., 1980; Bingham, 1993). It is also known that fixation is not perfect, and the gain of oculomotor compensation is lower than 1 during head-free fixation on nearby targets (Crane and Demer, 1997; Skavenski et al., 1979). Therefore, in additional simulations, we varied the compensation gain of eye movements to examine the impact of an imperfect fixation.

Fig. 9 summarizes the results of these simulations. Data points represent percent changes in the depth thresholds on the zero azimuth axis measured with three compensation gains (0, 0.5, and 0.8) relative to the case of perfect compensation (gain of 1). As shown by these data, the parallax introduced by eye rotations party counteracted the parallax resulting from head translations. That is, as the oculomotor compensation gain decreased, the nodal points moved farther away from the fixation axis, an effect that slightly reduced depth thresholds. However, this modulation was minimal and never exceeded 4% even in the case of no oculomotor compensation at all. In the more realistic case of gains above 0.5, changes in depth thresholds were smaller than 2% at all the considered distances. Thus, the reconstructions of retinal stimulation obtained under the assumption of perfect fixation in Figs. 5-8 provide accurate characterization of the parallax present during fixation irrespective of the particular oculomotor strategy adopted by the observer.

Fig. 9.

Influence of eye movements. Data points represent percent differences in the depth thresholds measured with different oculomotor gains (0, 0.5, and 0.8) relative to the case of perfect compensation (gain of 1). Targets were located on the Z axis. The fixation marker was at 50 cm. Errorbars represent one standard deviation.

4. Discussion

Visual fixation is an active process. Continual adjustments in body posture and small movements of the head incessantly alter the observer’s viewpoint. These displacements do not simply shift the entire image on the retina, but move the retinal projections of objects at different distances from the observer relative to each other. Our data show that this differential motion is larger than it may be intuitively assumed and that the resulting relative velocities are well above perceivable thresholds for a broad range of depths. These findings support the proposal that the parallax caused by fixational head movements is a reliable source of depth information, which humans may use in a variety of visual and visuomotor tasks.

Motion parallax is commonly studied within the context of major changes in the observer’s viewpoint, like, for example, those caused by large voluntary head movements (Rogers, 2009). Fixational head movements appear too small to yield a parallax that is perceptually relevant. However, studies on the visual control of posture have provided evidence that this assumption is not correct. It was first observed by Bronstein and Buckwell (1997) that body sway is influenced by motion in the scene simulating the parallax an observer would experience in a stable three-dimensional environment. These visuomotor responses continue to be present during monocular viewing, but do not occur when the point of fixation moves with the observer (Guerraz et al., 2001). Furthermore, postural stability improves during viewing of two visual references at different distances from the observer relative to presentation of only one reference or two references at the same distance (Guerraz et al., 2000). All these observations are consistent with a role of motion parallax in the control of body sway. More recently, Louw et al. (2007), quantified the relative contributions of different visual cues to depth judgments. These authors observed a consistent contribution from the motion parallax caused by small head movements. Our results join these previous findings in supporting a perceptual role for fixational head movements. They show that even under the conservative conditions of our experiments, in which observers were specifically instructed not to move while maintaining fixation, small changes in depth yield differences in retinal velocities that should be clearly detectable. Differential motion on the retina may be even more pronounced when subjects are not explicitly required to remain immobile and can explore the scene normally.

The results reported in this study are very robust. Head trajectories were measured at high resolution using a custom-developed tracking system. The position and orientation of the head in space were estimated by means of an optimization procedure on the basis of the positions of 20 LED markers. Control experiments, in which a robotic manipulator finely adjusted the position of a manikin head, have shown that this system possesses the linear and angular resolutions necessary to measure the small head movements that occur during fixation. Retinal image motion was estimated on the basis of two models: a geometrical model of head/eye kinematics and an optical model of the eye. The geometrical model was calibrated for each subject in a preliminary experimental session in which we estimated the location of each eye’s center relative to the head’s centroid. Given the little influence of head rotations on eye displacements (see Figs. 3 and 4), possible errors in the localization of the eye center would only marginally influence our estimates of differential velocity. The optical model is a standard model of the eye (von Helmholtz, 1924). Although the parameters of the model could vary with each individual eye and with accommodation, these changes would have little impact on our measurements. For example, changing the model parameters from the accommodated to the unaccommodated state only increased depth thresholds by less than 3% on the 0° eccentricity axis.

Our conclusions are also little affected by the specific oculomotor strategy that an observer may follow during fixation. If one neglects the offsets between the center of rotation of the eye and the positions of the optical nodal points, eye movements can be modeled as pure rotations; they shift the entire image on the retina without causing differential motion. However, because the optical nodal points of the eye do not coincide with the center of rotation, eye movements may contribute to differential motion on the retina (Hadani et al., 1980; Bingham, 1993). Since eye movements were not recorded in the experiments, we used computer simulations to examine their possible influence. With a compensation factor of 80%, the average gain measured during fixation in standing observers (Crane and Demer, 1997), the effect of eye movements was negligible. Thus, our estimates of retinal image motion obtained under the assumption of perfect fixation provide excellent approximation of the parallax present during different types of eye movements.

To summarize how accurately the parallax resulting from head displacements can be used for evaluating depth, we assumed a velocity sensitivity threshold of 1’/s. Previous studies have shown that, for slow head movements, thresholds for parallax only depend on relative speed. Ujike and Ono (2001) reported detection thresholds around 0.26′/s when the head moved slower than 13 cm/s, a range that includes the movements considered in this study. These threshold values are similar to those measured for detection of relative linear motion (Snowden, 1992; Shioiri et al., 2002) and sinusoidal motion (Nakayama and Tyler, 1981). Based on these previous findings, we conservatively assumed the value of 1’/s as the minimum detectable relative speed and determined the minimum change in depth that would overcome this threshold. Our results show that, up to 4 meters from the observer, most of the central region of the visual field yields signals that well exceed 1’/s. Thresholds for relative velocity will increase with eccentricity (McKee and Nakayama, 1984), but values of a few arcmin per second have been measured even at eccentricities as large as 30° (Lappin et al., 2009). Thus, the parallax resulting from fixational head movement may provide a reliable source of depth information in a large portion of the visual field.

A considerable body of evidence indicates that extraretinal signals are essential for properly interpreting parallax (Ono and Ujike, 1994; Domini and Caudek, 1999; Freeman and Fowler, 2000; Nawrot, 2003; Naji and Freeman, 2004). Early studies on head translations (e.g., Rogers and Graham 1979; Ono and Steinbach 1990) led to the assumption that a vestibular contribution may be necessary. However, more recent studies have shown that extraretinal signals related to eye movements are critical (Freeman and Fowler, 2000; Nawrot, 2003; Naji and Freeman, 2004). Vestibular signals are certainly present during small fixational head movements, as they contribute to the maintenance of balance (Paulus et al., 1987; Jessop and McFadyen, 2008) together with a variety of proprioceptive signals (Roll et al., 1989; Fitzpatrick and McCloskey, 1994). Compensatory eye movements that maintain the stimulus on the preferred retinal locus are also expected to occur, as reliable pursuit is elicited by very low velocities (Mack et al., 1979; Poletti et al., 2010). Thus, all the sensory signals necessary for properly interpreting parallax appear to be present during normal head-free fixation.

While the focus of this study is on parallax, it is important to note that fixational head movements may also serve other visual functions besides contributing depth information. Images tend to fade and may even disappear completely under retinal stabilization, an artificial laboratory condition that eliminates retinal image motion (Ditchburn and Ginsborg, 1952; Riggs et al., 1953; Yarbus, 1967). It has long been proposed that normal head movements could help preventing image fading during natural viewing (Kowler and Steinman, 1980). Indeed, the retinal velocities resulting from uncompensated head and body movements seem suffcient to preserve visibility (Skavenski et al., 1979) and elicit strong responses in cortical neurons (Sanseverino et al., 1979; Kagan et al., 2008). Our results provide support to this proposal. They show that retinal velocities higher than 20’/s—the limit to maintain full visibility (Ditchburn et al., 1959)— occur just because of parallax, even under the unrealistic assumption of perfect oculomotor compensation.

Fixational head movements may also contribute to properly structuring the input stimulus on the retina into a format that facilitates neuronal processing. We have recently shown that when images of natural scenes are examined with the head immobilized, microscopic eye movements equalize the spatial power of the stimulus on the retina over a broad range of spatial frequencies (Kuang et al., 2012). This transformation removes predictable correlations in natural scenes (Attneave, 1954; Barlow, 1961) and appears to be part of a scheme of neural encoding that converts spatial luminance discontinuities into synchronous firing events. When the head is not restrained, eye and head movements adaptively cooperate to maintain a specific amount of image motion on the retina (Collewijn et al., 1981). Simultaneous high-precision recordings of both head and eye movements are needed to investigate the frequency characteristics of the retinal stimulus under normal viewing conditions.

In sum, the retinal image motion resulting from continually occurring adjustments in posture and head movements may contribute to multiple visual functions. Our results show that even objects at small depth separations within the space nearby the observer yield significant differential velocities on the retina. These motion signals are likely to be accompanied by extraretinal eye and head movement signals, thus enabling effective use of parallax. Further work is needed to investigate how the visual system uses this information.

Highlights.

• Small head movements continually occur during natural fixation.

• We measured the differential motion in the retinal image resulting from these microscopic head movements.

• The parallax present during normal head-free fixation is a reliable source of depth information within the space nearby the observer.