Membrane Cholesterol Strongly Influences Confined Diffusion of Prestin

Abstract

Prestin is the membrane motor protein that drives outer hair cell (OHC) electromotility, a process that is essential for mammalian hearing. Prestin function is sensitive to membrane cholesterol levels, and numerous studies have suggested that prestin localizes in cholesterol-rich membrane microdomains. Previously, fluorescence recovery after photobleaching experiments were performed in HEK cells expressing prestin-GFP after cholesterol manipulations, and revealed evidence of transient confinement. To further characterize this apparent confined diffusion of prestin, we conjugated prestin to a photostable fluorophore (tetramethylrhodamine) and performed single-molecule fluorescence microscopy. Using single-particle tracking, we determined the microscopic diffusion coefficient from the full time course of the mean-squared deviation. Our results indicate that prestin undergoes diffusion in confinement regions, and that depletion of membrane cholesterol increases confinement size and decreases confinement strength. By interpreting the data in terms of a mathematical model of hop-diffusion, we quantified these cholesterol-induced changes in membrane organization. A complementary analysis of the distribution of squared displacements confirmed that cholesterol depletion reduces prestin confinement. These findings support the hypothesis that prestin function is intimately linked to membrane organization, and further promote a regulatory role for cholesterol in OHC and auditory function.

Introduction

The frequency selectivity, and sensitivity of mammalian hearing is enhanced by fast electromechanical coupling of transmembrane potential changes to rapid length changes in cochlear outer hair cells (OHC) (1–3). This unique form of cellular motion, termed electromotility, has a distinct electrical signature that manifests as a robust nonlinear capacitance (NLC) in the native OHC (4–6). The transmembrane protein prestin, expressed in the OHC lateral wall, has been identified as the motor that drives electromotility (7). Measurement of NLC as a test of prestin function has become standard and is characterized experimentally by measuring total charge movement and the voltage at peak capacitance $V_{pkc}.$ Mammalian cells, including HEK cells, that exogenously express prestin gain NLC (8–11) and have also been shown to exhibit voltage-induced motion (7), validating their use as a model system in place of the native OHC.

Prestin is predicted to have 10–12 membrane-spanning helices (10), and numerous studies have demonstrated the importance of understanding the interaction between prestin and the cell membrane. Various manipulations of the plasma membrane environment have been shown to affect prestin function. For example, amphiphilic drugs that alter prestin function also alter membrane curvature and mechanical properties (12,13), and membrane substitution with lipids of differing acyl-chain lengths shifts $V_{pkc}$ due to changes in membrane thickness (14). Prestin is generally considered to undergo a voltage-dependent conformational change that exerts force on the OHC lateral wall. Anisotropic lipid diffusion has been measured in OHCs, suggesting interactions of the OHC cytoskeleton with the membrane (15). Thus, manipulations that affect the organization and conformational flexibility of prestin could potentially affect prestin and OHC function.

Membrane cholesterol, a well-characterized modifier of prestin function, has received much attention because of its potential physiological importance. OHC cholesterol levels decrease during maturation of hearing in mice, and manipulation of cholesterol levels in live adult mice affects cochlear amplification (16). In both the OHC and HEK cells, depletion of membrane cholesterol shifts $V_{pkc}$ in the depolarizing direction, and loading of membrane cholesterol causes hyperpolarizing shifts (16–18). In addition, depletion of membrane cholesterol enhances the mechanical response of OHCs to electrical stimuli (19). Moreover, confocal fluorescence images of prestin-transfected cells show punctate foci in the membrane (16,17,20,21). Puncta reversibly disappear upon cholesterol depletion and colocalize with known lipid raft markers (16,17). The OHC lateral wall, where prestin is functional, has lower membrane cholesterol levels than the basal or apical regions (16), where electromotility is not present (22). Biochemical studies have shown the appearance of prestin in raft fractions of membrane lysate (16,17) that decrease upon depletion of membrane cholesterol. Taken together, these findings suggest an important role for cholesterol and microdomains in regulating prestin function, and motivate the measurement of prestin diffusion to characterize possible interaction of prestin with membrane compartments. Clearly, precise knowledge about whether cholesterol alters the microscale organization of prestin in the membrane is needed to interpret existing data.

Measuring protein diffusion in living cell membranes is a powerful way to characterize the interactions of membrane proteins with membrane substructures (23). Early indications that prestin is mobile came from indirect electrophysiological measurements (24,25). Later, direct measurements of prestin diffusion employing fluorescence recovery after photobleaching (FRAP) revealed that immobile fractions remained after dual bleaches, suggesting that prestin is transiently confined (20). However, because FRAP is an ensemble measurement, a detailed analysis of the size and character of the putative confinements was not possible, and other, more-complex modes of diffusion could not be ruled out (20). Thus, several questions remain to be resolved. For example, does prestin diffuse within confinement zones or can it become immobile due to binding with structures in the membrane? Furthermore, does prestin remain confined or can it diffuse or hop into other compartments? Are these processes dependent on cholesterol?

To study prestin diffusion at a finer level of detail, one must track single prestin molecules. Single-particle tracking (SPT) is a powerful method that is commonly applied to study the diffusion of membrane proteins and lipids at the single-molecule level (26). In recent years, advances have been made in analyzing and interpreting the motion of molecules confined to membrane compartments (27–29). In particular, the importance of the effects of detector averaging and time resolution on confined diffusion (27,30) have been characterized, and methods to correct for these effects have been developed (28,29). In this study we use SPT of prestin, conjugated to a minimally disruptive fluorescent tag, to measure prestin lateral mobility and investigate the effect of cholesterol on prestin diffusion. We interpret our data using an analytical approximation to hop-diffusion developed by Wieser et al. (28) and by a complementary statistical analysis of the full distribution of squared displacements (31). We find that prestin undergoes confined diffusion in relatively large confinements, and its diffusive behavior is significantly affected by membrane cholesterol levels.

Materials and Methods

Details regarding the creation of a plasmid encoding for prestin-SNAP-tag, cell culture, transfection, and labeling procedures are provided in the Supporting Material. Also described in the Supporting Material are the methods used to calculate prestin trajectories and the mean-squared deviation (MSD), and to characterize the effects of detector averaging and localization precision, which are needed for the detailed analysis of MSD and step-size distributions described below.

Cell treatments

To deplete membrane cholesterol, we used a protocol similar to that described by Sfondouris et al. (18), which removes $\sim 60\%$ of cholesterol from the membrane fraction of HEK293 cells as determined using the Bradford method and the Amplex Red Cholesterol Assay (Molecular Probes, Eugene, OR). Transfected HEK293 cells were given a 20 min treatment of 10 mM methyl-β-cyclodextrin (MβCD) in serum-free Dulbecco’s modified Eagle’s medium at 37°C and washed before imaging in HEPES buffered saline. For control experiments, in which immobile prestin was imaged, cells were fixed in 4% paraformaldehyde for 10 min before imaging.

Single-molecule microscopy

Complete details of our imaging protocol are provided in the Supporting Material. Briefly, transfected cells are imaged using objective type total internal reflection fluorescence (TIRF) microscopy. For each cell, 200-frame image stacks containing diffraction-limited signals in each frame are collected (see Movie S1 and Movie S2). A characterization of nonspecific labeling is provided in the Supporting Material and Movie S3, Movie S4, and Movie S5. The locations of the signals are determined in each frame using software developed in-house with MATLAB (The MathWorks, Natick, MA) and correlated between frames to construct 2D trajectories. The MSD is calculated from an ensemble average of all the trajectories as described in the Supporting Material.

Analysis of MSD

To describe the measured MSD, we use the analytical hop-diffusion model developed by Wieser et al. (28). This model extends the exact calculation (32) of MSD for a particle totally confined to a corral of size L to an array of partially permeable corrals using an analytical approximation. Wieser et al. (28) included corrections for the effects of time averaging (27,28,30,33) over the finite exposure time $t_{ill}$. For the MSD, they find

$$MS{D}_{hop}\left(t_{lag}\right)=\alpha \left\{\frac{\alpha L^2}{3}-\frac{32\alpha L^2}{{\pi }^4}\sum _{k=1\left(odd\right)}^{\infty }\frac{1}{k^4}\text{exp}\left[-{\left(\frac{k\pi }{L}\right)}^2\frac{D_{micro}}{\alpha }{t}_{lag}\right]\right\}\times \frac{1}{1+\frac{4D_{micro}{t}_{ill}}{L^2}}+4D_{macro}\left(t_{lag}-\frac{1}{3}{t}_{ill}\right),$$ (1)

where $D_{micro}$ is the microscopic diffusion constant the particle would have in the absence of confinement, and $t_{lag}$ is the time lag. $D_{macro}=\left(1-\alpha \right)D_{micro}=1/\hat{\tau }{D}_{micro}$ is the macroscopic diffusion constant the particle appears to have over long observation times and describes the hopping between corrals. α is the probability that the particle will remain confined, which sets $D_{macro},$ and is related to the confinement strength $\hat{\tau }=D_{micro}/D_{macro}$ within the domains by $\hat{\tau }=1/1-\alpha$ (by definition, $\hat{\tau }\ge 1$ with $\hat{\tau }\to \infty /1$ signifying totally impermeable/permeable barriers). To fit the $\text{MSD}\left(t_{lag}\right)$ data with the hop-diffusion model, we truncated the summation in Eq. 1 out to six terms to define our fitting function ${\text{MSD}}_{fit}\left(t_{lag}\right)$. We found estimates of the three fitting parameters ($D_{micro},$ L, and α) by minimizing ${\chi }^2={\sum }_{t_{lag}}{\left[1/{\sigma }_{\mathit{MSD}}\left(t_{lag}\right)\left(MSD\left(t_{lag}\right)-MS{D}_{fit}\left(t_{lag}\right)\right)\right]}^2,$ where weighting factor ${\sigma }_{\mathit{MSD}}^2\left(t_{lag}\right)$ is the variance of MSD at each $t_{lag},$ using least-squares fitting (34) by the Levenberg-Marquardt method in Origin (Northampton, MA). The error in each fit parameter is the one-σ confidence interval determined by finding the range in that parameter, around the best fit, that produces $\Delta {\chi }^2=1$ while allowing the other two parameters to vary. The confinement offset CO_corr, corrected for effects of detector averaging, is calculated from the fit parameters α and L according to $C{O}_{corr}={\alpha }^2{L}^2/3$ (28). The error in CO_corr using Gaussian error propagation (34) is ${\sigma }_{C{O}_{corr}}=2/3\alpha L{\left(L^2{\sigma }_{\alpha }^2+{\alpha }^2{\sigma }_L^2\right)}^{1/2},$ where ${\sigma }_{\alpha }$ and ${\sigma }_L$ are the respective one-σ errors in α and L. The error in the confinement strength $\hat{\tau }$ is ${\sigma }_{\hat{\tau }}={\left(1/1-\alpha \right)}^2{\sigma }_{\alpha }.$ The error in $D_{macro}$ is ${\sigma }_{D_{macro}}={\left({\left(1-\alpha \right)}^2{\sigma }_{D_{micro}}^2+D_{micro}^2{\sigma }_{\alpha }^2\right)}^{1/2}.$

Analysis of step-size distribution

The calculation of the squared step-size probability density distribution $p\left(\Delta r^2,t_{lag}\right)$ was achieved by binning individually measured squared displacements $\Delta r^2$ at either $t_{lag}=250.8ms$ or $1.254s$ for all trajectories combined, and normalizing the result to the total number of observed step-displacements. The cumulative distribution function (CDF) $P\left(\Delta r^2,t_{lag}\right)$ was calculated by cumulatively summing the $p\left(\Delta r^2,t_{lag}\right)$ histogram (31):

$$P\left(\Delta r^2,t_{lag}\right)=\underset{0}{\overset{\Delta r^2}{\int }}d\Delta r^{\prime 2}p\left(\Delta r^{\prime 2},t_{lag}\right).$$ (2)

Experimentally measured CDF was fit to a function describing one diffusive component,

$$P\left(\Delta r^2,t_{lag}\right)=1-\epsilon \text{exp}\left(\frac{-\Delta r^2}{r_o^2}\right)-\left(1-\epsilon \right)\left(1-F\left(\Delta r^2\right)\right),$$ (3)

with two free parameters $r_o^2$ and ɛ. The function $F\left(\Delta r^2\right)$ represents the CDF of apparent displacements measured for immobilized particles in fixed cells (see Results and Fig. S3 in the Supporting Material), and ɛ is the fraction of the diffusive component with characteristic squared diffusion length $r_o^2.$ Detector time averaging effects (33) and effects of positional uncertainty (35) are taken into account for $r_o^2$ by assuming $r_o^2\approx 4D{t}_{lag}+\Delta -\left(4/3\right)D{t}_{ill}.$ See the Supporting Material and Fig. S1, Fig. S2, Fig. S3, and Fig. S5 for a detailed analysis of detector averaging and positional accuracy effects.

Results

SPT of prestin

We measured the trajectories of prestin-SNAP-tag labeled with tetramethylrhodamine (TMR)-conjugated benzylguanine (BG) substrate, which has the advantage of preventing both cross-linking of prestin (due to one-to-one binding stoichiometry of BG to SNAP-tag) and long observation times (due to the photostability of TMR). Shown in Fig. 1 are sample prestin-SNAP-TMR trajectories in untreated cells. The displayed trajectories are relatively long (ranging from $\sim 8-48s$ or ∼30–190 observed time steps) compared with the average trajectory length of ∼$9s.$ The trajectories display what appear to be subregions of confinement varying in apparent size. The locations of the confinement zones in some of the examples appear to hop in position, and in others the trajectories appear to be confined to a single localized region.

Figure 1.

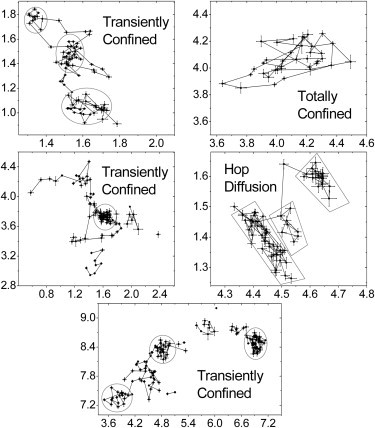
Sample trajectories of BG-TMR-labeled prestin-SNAP-tag molecules in untreated HEK cells. Coordinate axes are the position in μm. The frame time is 250.8 ms for all trajectories. Error bars in position are fitting errors from Gaussian fits (Eq. S1) to spot intensity profiles. The displayed sample trajectories were chosen for presentation based on longer-than-average diffusion times before bleaching. Gray shapes outline plausible apparent confinement regions. Discontinuities in some trajectories are due to cases in which the analysis software failed to detect the fluorescent signal in one or more frames. In these cases, it was visually clear that the signal was the same as that in subsequent frames.

Because many tracks are too short to clearly observe the confinement of motion in a single trajectory (36), we calculated the MSD of all recorded tracks for each of two groups (control and cholesterol depleted) using Eq. S3. We first analyzed prestin motion in untreated cells (Fig. 2, A (solid circles) and B). As expected for confined diffusion, the rise of $\text{MSD}\left(t_{lag}\right)$ clearly changes to a drastically shallower slope as $t_{lag}$ increases. We also measured the MSD of prestin in cells treated with 10 mM MβCD (Fig. 2, A and C, open circles). In this case, we also observe a decrease in the slope of $\text{MSD}\left(t_{lag}\right)$ at long $t_{lag}$; however, the change in slope is less obvious. To obtain quantitative estimates of quantities related to confined diffusion, we performed fits (shown in Fig. 2, A–C, red curves) of $\text{MSD}\left(t_{lag}\right)$ for untreated and MβCD-treated groups to a hop-diffusion model using Eq. 1 (28). Due to the large variance in $\text{MSD}\left(t_{lag}\right)$ at long $t_{lag},$ we restricted our analysis to $t_{lag}\le 30s.$

Figure 2.

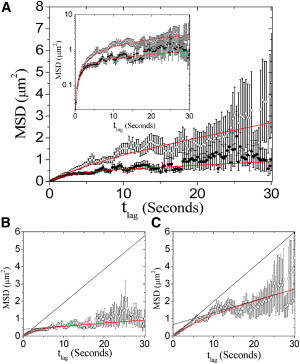
MSD versus time for prestin-SNAP-TMR. (A) Measured MSD against $t_{lag}$ in untreated (solid circles) and cholesterol-depleted (open circles) cells. A total of 285 tracks were recorded for untreated cells (nine cells), and 269 tracks were recorded for cells treated with 10 mM MβCD (seven cells). Error bars are standard error of the mean. Increased variance at long $t_{lag}$ result from decreased probability of observing long trajectories due to photobleaching of TMR. Both data sets are fit to the hop-diffusion model (Eq. 1, solid curve). Inset: Data are shown on a log scale to emphasize fit to early points. The resulting fitting parameters are (for untreated cells) $\alpha ={0.908}_{-0.016}^{+0.018}$, $L={1.215}_{-0.054}^{+0.057}\mu m$, and $D_{micro}={0.0481}_{-0.0027}^{+0.0029}\mu m^2/s$ with ${\chi }_{\nu }^2=0.6$; and (for cells treated with MβCD) $\alpha ={0.659}_{-0.039}^{+0.039}$, $L={2.15}_{-0.14}^{+0.14}\mu m$, and $D_{micro}={0.0499}_{-0.0018}^{+0.0018}\mu m^2/s$ with ${\chi }_{\nu }^2=0.67$. Asymptotic behavior (black curves) of MSD_hop for (B) untreated and (C) MβCD-treated groups is shown superimposed on data and fit (red curves). According to the hop-diffusion model, including averaging effects, ${\text{MSD}}_{hop}(t_{lag}\to 0)=4D_{micro}(t_{lag}-(1/3)t_{ill})$ and $MS{D}_{hop}(t_{lag}\to \infty )=CO+4D_{macro}{t}_{lag}$, where $CO=(L^2{\alpha }^2/3){(1+(4D_{micro}{t}_{ill}/L^2))}^{-1}-(4/3)\left(1-\alpha \right)D_{micro}{t}_{ill}$ is a confinement offset seen as the y-intercept in B and C (28). Macroscopic diffusion constants $D_{macro}$ : (B) $4.4\pm 0.9\times {10}^{-3}\mu m^2/s$ and (C) $0.017\pm 0.002\mu m^2/s$.

From the fit to the MSD of the control group, we conclude that the average microscopic diffusion constant of prestin within confinement zones in the HEK plasma membrane is $D_{micro}={0.0481}_{-0.0027}^{+0.0029}\mu m^2/s.$ We obtained fitted values for L and α of ${1.215}_{-0.054}^{+0.057}\mu m$ and ${0.908}_{-0.016}^{+0.018},$ respectively. Using the fitted values and uncertainties of L and α, we calculate the corrected confinement offset (i.e., the offset that is produced only by diffusion within and hopping between domains) to be $C{O}_{corr}=0.406\pm 0.041\mu m^2.$ Instead of quoting the fitted value of L as our estimate for the average domain size, we make a more conservative estimate by calculating the full range in L implied by letting α and the confinement offset $C{O}_{corr}$ vary by their maximum uncertainty ranges; this gives L in the interval $\left(1.13,1.30\right)\mu m.$ The value obtained for α implies that the confinement strength is $\hat{\tau }=11\pm 2.$ This indicates strong confinement, which is consistent with the nearly flat slope of $\text{MSD}\left(t_{lag}\to \infty \right)$ at large time lags (Fig. 2 B).

Results from fitting the MβCD-treated group indicate that, within the fitting error, the microscopic diffusion constant $\left(D_{micro}=0.0499\pm 0.0018\mu m^2/s\right)$ is unchanged by depletion of membrane cholesterol. However, we found that the average domain size L is increased to be in the range of $\left(1.85,2.48\right)\mu m$. In addition, the MβCD-treated group shows a marked decrease in the confinement strength (and concomitantly a decrease in α) to $\hat{\tau }=2.9\pm 0.3$. This is reflected in the higher slope of $\text{MSD}\left(t_{lag}\to \infty \right)$ displayed in Fig. 2 C.

Cumulative distribution function of squared step-size

To explore prestin diffusion in greater detail than is possible with analysis of the MSD, one must have full statistical knowledge of the step-size distribution. We therefore measured the probability density of squared step size $p\left(\Delta r^2,t_{lag}\right)$ and from it measured the cumulative distribution function (CDF) of squared step size $P\left(\Delta r^2,t_{lag}\right)$ (Eq. 2). The CDF gives the probability that after time $t_{lag}$, the particle will still be found within a squared radius $\Delta r^2$ from where it started (31).

We initially reasoned that we should measure the CDF at the shortest possible time lag of $t_{lag}=250.8ms$ because on that timescale the average step size would be $\approx {\left(4D_{micro}{t}_{lag}\right)}^{1/2}=220nm$, which is less than the average domain size (29) obtained from MSD analysis for both treatment groups. However, detector averaging has a noticeable effect on the CDFs at $t_{lag}=250.8ms$, where $t_{lag}$ is nearly equal to the exposure time $t_{ill}=250$ ms (see Supporting Material and Fig. S4 and Fig. S5 for a detailed discussion and analysis). We therefore recalculated $P\left(\Delta r^2\right)$ at a longer $t_{lag}$ of $1.254s$ for both treatment groups (Fig. 3). At this longer time lag, detector averaging would only have a 7% effect on $4D_{micro}{t}_{lag}$ for free diffusion. Furthermore, at $t_{lag}=1.254s$, the time lag is still below $L^2/4D_{micro}$ implied by the average domain size for both groups, and therefore simple Brownian diffusion is expected (29). For pure Brownian motion, the expectation is that $P\left(\Delta r^2\right)=1-\text{exp}\left(-\Delta r^2/r_o^2\right)$, where $r_o^2$ is the characteristic diffusive step. However, we found that fits to a simple Brownian model significantly deviated from both untreated and MβCD CDFs (Fig. 3, dashed curves).

Figure 3.

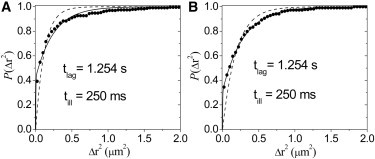
CDF of squared step size at increased time lag. For both groups, only displacements used to calculate $\text{MSD}\left(t_{lag}=1.254s\right)$ are included. Bin size is $\delta r^2=0.04\mu m^2$. CDF (solid circles) is fit to Eq. 3 (solid curves). Also shown for comparison is a fit to a simple exponential $P\left(\Delta r^2,t_{lag}\right)=1-\text{exp}\left(-\Delta r^2/r_o^2\right)$ (dashed curves). (A) A fit to the untreated group using Eq. 3 gives $r_o^2-\Delta =0.250\mu m^2$ and $\varepsilon =0.575$. (B) A fit to the MβCD-treated group using Eq. 3 gives $r_o^2-\Delta =0.288\mu m^2$ and $\varepsilon =0.685$. Because the diffusive portion of the MβCD group fits perfectly with free diffusion, it is appropriate to obtain the diffusion constant. We obtain $D=0.0615\mu m^2/s$. The variance of the fit to the MβCD-treated group ($S^2=2.67\times {10}^{-3}$) is more than a factor of 10 smaller than the variance of the fit to the untreated group ($S^2=2.76\times {10}^{-2}$).

We next explored possible effects that could cause deviations from a pure exponential function predicted for pure Brownian motion. First, we considered that if there were a broad distribution of domain sizes L, confined displacements within the smallest domains would appear immobile (27–30). In particular, displacements within impermeable domains of an actual size $\ll \sim 95nm$ would appear to be <$22nm$, below the position resolution of our system, and hence indistinguishable from immobile displacements. We therefore characterized the apparent squared step-size distribution $f\left(\Delta r^2\right)$ for immobile prestin-SNAP-TMR in fixed cells and from it determined the CDF $F\left(\Delta r^2\right)={\int }_0^{\Delta r^2}d\Delta r^{\prime 2}f\left(\Delta r^{\prime 2}\right)$ (Fig. S3). For a constant positional uncertainty ${\sigma }_{xy}$, $f\left(\Delta r^2\right)$ should be a monoexponential $f\left(\Delta r^2\right)\sim e^{-\Delta r^2/4{\sigma }_{xy}^2}$, which would give $F\left(\Delta r^2\right)=1-e^{-\Delta r^2/4{\sigma }_{xy}^2}$. However, not surprisingly, the experimentally measured $f\left(\Delta r^2\right)$ and $F\left(\Delta r^2\right)$ in Fig. S3 do not fit to a monoexponential because, as demonstrated in Fig. S1C, there is a distribution $g\left({\sigma }_{xy}\right)$ of standard deviations with spread ${\sigma }_{{\sigma }_{xy}}$ about the average ${\overline{\sigma }}_{xy}$, which we approximate by $g\left({\sigma }_{xy}\right)\sim e^{-{\left({\sigma }_{xy}-{\overline{\sigma }}_{xy}\right)}^2/2{\sigma }_{{\sigma }_{xy}}^2}$. This will have the effect of smearing the exponential distribution in the following fashion:

$$f_{smear}\left(\Delta r^2\right)\sim \underset{0}{\overset{\infty }{\int }}d{\sigma }_{xy}g\left({\sigma }_{xy}\right)f\left(\Delta r^2\right)\sim \underset{0}{\overset{\infty }{\int }}d{\sigma }_{xy}{e}^{-{\left({\sigma }_{xy}-{\overline{\sigma }}_{xy}\right)}^2/2{\sigma }_{{\sigma }_{xy}}^2}{e}^{-\Delta r^2/4{\sigma }_{xy}^2}.$$ (4)

To calculate this integral, we simulated $f_{smear}\left(\Delta r^2\right)$ numerically (Fig. S2) with the measured parameters ${\sigma }_{{\sigma }_{xy}}$ and ${\overline{\sigma }}_{xy}$, and integrated to obtain $F\left(\Delta r^2\right)$. The result of the simulation is in excellent agreement with the measured CDF (Fig. S3). This demonstrates that in Fig. 3 we have correctly accounted for the apparent motion of molecules that are either immobile or confined to corrals that are not resolvable with our spatial and temporal resolution.

When we fit both control and MβCD groups to Eq. 3, now with the inclusion of $F\left(\Delta r^2\right)$ (Fig. S3) to account for the apparent immobility of displacements within small corrals, we found that the CDF of the untreated group still showed deviations from a single diffusive component (Eq. 3) because the CDF rises quicker than the monoexponential fit (Fig. 3 A, solid curve). This indicates the influence of barriers to free diffusion in untreated cells that are encountered during the 1.254s diffusion time window. However, the diffusive portion of the MβCD-treated group fit perfectly to a monoexponential (Fig. 3 B, solid curve). The variance of the fit to the MβCD CDF is more than a factor of 10 lower than that of the fit to the CDF of the untreated data (Fig. 3). The diffusive portion of the MβCD CDF implies a diffusion constant of $D=0.06\mu m^2/s$ and a diffusive fraction of $\varepsilon =0.685$.

Discussion

Analysis of MSD reveals that prestin undergoes slow diffusion in permeable confinements

We first analyzed the MSD of prestin and obtained estimates of the domain size, confinement strength, and microscopic diffusion constant for untreated and MβCD-treated groups. We estimated a relatively small diffusion constant even for $D_{micro}$ compared with the majority of other membrane proteins examined in studies using SPT, which typically report diffusion constants on the order of 0.1–1$\mu m^2/s$ (28,36,37). However, our low estimate for D is consistent with previous slow estimates obtained with FRAP (20,38). The slow diffusion of prestin offers an opportunity to measure the full time course of the MSD describing hop diffusion, thereby enabling a precise determination of $D_{micro}$ using a modest frame rate. It also enables us to confidently discriminate between confined diffusion and free diffusion. Our observations directly confirm the hypothesis of Organ and Raphael (20) that prestin undergoes transiently confined diffusion in HEK cells.

As a technical note, we cannot fully distinguish confined diffusion within small corrals from immobility because we are limited in our spatiotemporal resolution. Thus, we cannot rule out the occurrence of transient binding of prestin to other slow or immobile proteins in or near the membrane. The recent report that prestin binds the microtubule-associated protein MAP1S (39) provides a possible candidate for a binding partner in addition to CFTR (40), although it is unknown whether these proteins are constitutively expressed in HEK cells. Furthermore, transient binding could explain the unusually low $D_{micro}$ we estimate compared with other proteins. However, we can rule out the possibility that we mistook transient binding for confinement, because the former cannot cause the initial rising phase in MSD observed in Fig. 2, A and B. In other words, our data indicate that prestin undergoes confined diffusion and may also participate in transient binding.

Large confinements are modified by cholesterol

MSD analysis reveals confinement of prestin to regions of an average size $\left(L\gtrsim 1\mu m\right)$ that is large compared with that obtained in some other studies (28,36,37,41). Even though L may be overestimated from fitting to the MSD because of a broad confinement size distribution, the average confinement area L² is still a proper estimate according to Wieser et al. (28). Furthermore, the average size for confinements in control cells is close to that reported for lipid microdomains in other cell types (42,43). For control cells, the average confinement area is in the range (1.27, 1.69) $\mu m^2$, and for cells depleted of membrane cholesterol, the average confinement area is increased to be in the interval (3.4, 6.1) $\mu m^2$. A large confinement size is also consistent with observations of puncta in prestin-transfected HEK cells that are clearly resolvable with confocal microscopy (16,17,20,21). The reversible disappearance of puncta upon depletion of membrane cholesterol has also been well established (16,17). This is consistent with our result (Fig. 2) that depletion of membrane cholesterol reduced the confinement strength from $11\pm 2$ to $2.9\pm 0.3$, because as $\hat{\tau }\to 1$, free diffusion is recovered (28). For confinements that are of equal size and large enough to observe with conventional microscopy ($\sim 500nm$), the residence time of prestin in confinements within untreated cells would be nearly four times longer than those in MβCD-treated cells, making confocal fluorescence images more diffuse in the latter case.

Analysis of CDF demonstrates that cholesterol depletion removes confinements

MSD analysis only provides the time evolution for the mean of the distribution of squared displacements. Furthermore, a broad confinement size distribution would violate the assumption of a perfectly periodic lattice on which the hop-diffusion model is based (28). We therefore analyzed the distribution in its entirety at select time lags to provide a complementary method that yields more detailed information.

To reduce the effects of detector averaging, we measured the CDFs at a time lag of 1.254s (Fig. 3). Minimal effects on the probability density should be seen at this time lag if the size of the confinements satisfy $L>{\left(4D_{micro}{t}_{lag}\right)}^{1/2}\approx 500nm$ (28,29,32). Fits to the CDF showed deviations from a single freely diffusive component for the diffusive fraction of the untreated group (Fig. 3 A), indicating that confinements exist in a size range between that which would lead to apparent immobility (by this we mean confinements small enough that the fluctuations in squared displacement with our time resolution would appear less than the localization offset Δ) and $500nm$. In contrast, the CDF for the MβCD-treated group fit perfectly with an apparently immobile component and a single, freely diffusing mobile component (Fig. 3 B). This observation provides strong evidence that depletion of membrane cholesterol reduces the number of barriers to free diffusion, possibly due to removal of cholesterol-rich microdomains. We can estimate an upper bound for the size of the putative small confinements that remain after cholesterol depletion by considering the largest confinement size for which motion would appear immobile at a time lag of 1.254s with 250ms averaging time. By solving $MS{D}_{hop}(t_{lag}=1.254s;\alpha =1,L^2)=\Delta$ for L, where Δ is the localization error offset (see Results in the Supporting Material and Fig. S1 B for measurement of Δ), we calculate an upper bound of 142nm. A more realistic estimate for a lower bound on the size of the large confinements is given by $L>{\left(12D_{micro}{t}_{lag}\right)}^{1/2}=867nm$ (32). In other words, after cholesterol depletion, we see no evidence of confinements between 142 and 867nm.

Possible origins of confinement

Our results demonstrate that membrane cholesterol is a major source of confinement for prestin in the HEK cell. Previous biochemical studies showed a decrease of prestin in the raft fraction containing flotillin-1 and integrin2α/VLA-2α, which are known membrane microdomain markers, and a relative increase in heavier membrane fractions for depletion of cholesterol using sucrose density gradient fractionation (16,17). However, a decrease in the microdomain markers was also observed, indicating that the reduction of prestin in the raft fraction may be a result of raft removal and concomitant removal of prestin. Furthermore, prestin diffusion measured using FRAP showed no increase in prestin mobile fraction for cholesterol depletion (38). In addition, Sfondouris et al. (18) reported that cholesterol depletion in transfected HEK cells did not increase prestin-associated charge movement (which the authors attributed to endocytosis of prestin caused by MβCD) even though loading cholesterol reduced charge movement. Together with our observation that some confinements remain upon cholesterol depletion, these previously obtained results tend to argue against a simple redistribution of prestin out of domains that do not change in size. Instead, we envisage that a fraction of prestin molecules undergo confined diffusion in cholesterol-rich microdomains and another portion is confined in the lower-cholesterol regions between the microdomains. The microdomains are probably superimposed on a heterogeneous membrane environment including a cytoskeletal meshwork. In this scenario, depletion of cholesterol makes the microdomains smaller and/or reduces their number. Both scenarios would increase the area between microdomains and increase the relative amounts of prestin in the low-cholesterol regions (which are now effectively larger confinements), explaining the larger average L² for the MβCD-treated group extracted from MSD analysis (Fig. 2), and our observation of an apparent removal of barriers to diffusion (Fig. 3).

It is interesting that cholesterol depletion preserves a significant portion of small confinements, suggesting that many of them (i.e., those <142 nm) may not be part of the detergent-resistant membrane fraction and instead may be confinements due to the cytoskeleton. It is worth noting that cytoskeletal confinements to DOPE (a phospholipid probe) 68nm in size have been found in HEK293 cells at $25\mu s$ resolution (44), and could be the identity of the small confinements that remained after cholesterol depletion in our study. Although we have not performed cytoskeletal treatments, it is possible that the domains are contained within or bound to cytoskeletal fences, or that prestin has a direct interaction with the cytoskeleton, conforming to the anchored-protein picket model and/or the membrane-skeleton fence model (37,45,46). Prestin has a large cytoplasmic domain, STAS (47), and it is not unreasonable to assume that part of the confinement to prestin after cholesterol depletion involves corralling of STAS with the cytoskeleton. Of interest, these models generally propose that the membrane protein confinement size should usually be unaffected by membrane cholesterol (46). The observation that prestin confinement size is clearly dependent on cholesterol is still consistent with the anchored-protein picket model because the density of pickets could be cholesterol dependent. Alternatively, MβCD could have secondary effects on the cytoskeleton. MβCD may directly affect the cytoskeleton or indirectly affect proteins that contribute to the organization of the cytoskeleton (48,49). Indeed, multiple studies have reported cholesterol-dependent membrane confinements coexisting with cholesterol-independent confinements (50–52), and our results suggest that this is likely the case with prestin.

Cholesterol depletion does not modify microscopic diffusion constant

Of interest, we found that cholesterol depletion did not change the microscopic diffusion constant of prestin in HEK cells. This is in agreement with FRAP results (38) that also showed no change in the effective diffusion constant with cholesterol depletion. Lipid diffusion in HEK cells also shows no change in D upon depletion of membrane cholesterol (53). This is in contrast to OHCs in which lipid lateral mobility is dependent on cholesterol and seems to be tuned to maximize lipid fluidity at native cholesterol concentration (53). These results partially support the hypothesis that alterations in prestin function observed after cholesterol loading of HEKs ($V_{pkc}$ shift and charge density reduction) result from decreases in membrane fluidity that restrict the conformational flexibility of prestin (18). However, this interpretation is inconsistent with the observation that lipid mobility is actually decreased for cholesterol depletion in OHCs (53), because that should cause a hyperpolarizing shift in $V_{pkc}$, whereas a depolarizing shift is actually observed (16). Furthermore, lipid mobility in HEK cells is insensitive to cholesterol depletion (53) while $V_{pkc}$ shifts remain (16–18). Thus, our results taken together with previous findings imply that cholesterol depletion affects prestin function by a mechanism other than changes in overall membrane fluidity.

Cholesterol and prestin function

It was previously suggested that cholesterol may affect prestin function by modifying the overall mechanical properties of the membrane (e.g., stiffness, compressibility, and thickness), either directly or by changing cytoskeleton membrane association (16,18,54). However, our results raise the possibility that prestin sensitivity to cholesterol is related to participation with ordered domains that depend on cholesterol such as lipid rafts. These two concepts are not mutually exclusive. Prestin residing within lipid rafts may function differently from prestin outside the domains, due to a direct interaction either with cholesterol or with the local environment. Therefore, cholesterol depletion may tune NLC by removing a functionally distinct prestin population from membrane microdomains and increasing the contribution of prestin outside the microdomains to whole-cell properties. Prestin molecules within the DRM fraction could have altered function because 1), lipid rafts increase or force prestin-prestin interactions that affect function; 2), prestin molecules within lipid rafts are brought near other raft-associated molecules (such as cholesterol or other raft-associated proteins) that affect function; or 3), prestin molecules in the lipid rafts have reduced conformational flexibility that affects $V_{pkc}$. Scenario 1 is supported by studies that demonstrated that prestin oligomerization can effect NLC (55), and that changes in membrane cholesterol may affect prestin oligomerization (16). The fact that prestin colocalizes with integrin molecules (16,17) and caveolin (21) indirectly supports scenarios 2 and 3, because both are often found as components of large protein-lipid clusters that are likely to have decreased fluidity and increased molecular crowding (56,57), which could affect the conformational flexibility of prestin.

Relevance to prestin function in OHCs

Thus far, we have discussed how our observations relate to membrane organization and prestin-associated charge movement (NLC) in HEKs. However, prestin in the OHC generates a robust electromechanical motion, and the interaction of prestin with the OHC cytoskeleton is an important research area (58,59). The cytoskeleton of the OHC consists of a cortical lattice comprising oriented domains of actin filaments that are bridged to the plasma membrane by pillar structures of unknown origin (60–63). There is evidence for structural (64) and functional (65) domains in the OHC, and the cytoskeletal structure of the OHC could define domains in the OHC plasma membrane. OHCs in prestin-null mice lack this organized cytoskeletal structure, suggesting that prestin is required to maintain it (66). Recently, it was shown that actin depolymerization mediated by LIM-kinases/Rho-GTPases regulates electromotility (67,68). This type of cytoskeletal reorganization would likely result in changes to prestin diffusion and confinement. Although the detailed nature of prestin-cytoskeletal interactions in HEK cells and OHCs is not fully understood, it is reasonable to expect that conserved physiological mechanisms are present, because there is a dynamic interdependence between cytoskeletal and membrane organization in all cell types. Furthermore, prestin charge movement has the same sensitivity to cholesterol manipulations when it is expressed in OHCs or HEK cells, suggesting that prestin sensitivity to cholesterol is likely not critically dependent on the unique structure of OHCs. Thus, a characterization of prestin diffusion and confinement in the HEK cell provides an important model system for understanding prestin organization and function in the OHC.

Conclusions

In this study, we characterized prestin diffusion in the HEK cell using SPT. A comparison of the full time course of MSD with a hop-diffusion model demonstrates that prestin undergoes confined diffusion in a broad size range of confinements. Depletion of membrane cholesterol increases the average confinement size and reduces the confinement strength, consistent with the observation that cholesterol depletion reversibly abolishes punctate fluorescence of prestin-transfected cells. These results support the view that a portion of prestin localizes to cholesterol-rich microdomains and that membrane cholesterol is a major source of prestin confinement. An analysis of the statistical distribution of squared displacements (CDF analysis) supports the results of fitting MSD to a hop-diffusion model. Depletion of membrane cholesterol removes barriers to free diffusion, resulting in a greater average confinement size. We hypothesize that cholesterol affects prestin function by modifying its interactions with membrane substructures. Although more research is needed to determine whether the ability of cholesterol to modulate prestin function results from effects related to prestin organization or to overall modifications of passive membrane mechanical properties, our observations add support to the growing view that the microscale organization of prestin in the plasma membrane influences prestin function.