Figure 2.
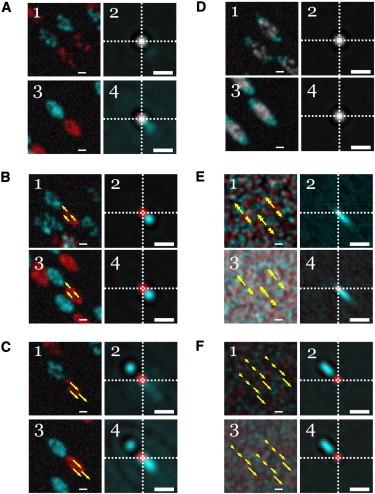
Simulation results and their resulting ACFs obtained via STICCS analysis for the following particle/macroscopic adhesion models: (A) Treadmilling, where adhesions flow due to particle addition/removal at the ends but particles inside the adhesion masks are static. (B) Sliding, where particles and adhesion masks flow together. (C) Antisliding, with particles flowing in the opposite direction of the adhesion masks (so peak separation can be visualized). (D) Spreading of immobile adhesion masks with immobile particles. (E) Particles undergoing anisotropic diffusion and flow in free space. (F) Dispersed flow of four particle populations with different but narrowly distributed velocities. Each model was analyzed for lower and higher particle densities (5 particles/μm2, top panels in each square; and 50 particles/μm2, bottom panels in each square). Each odd-numbered panel shows the superposition of the first and 100th frames (t = 1 and 100 s) from a single image series while each even-numbered panel shows the superposition of the corresponding ACFs at two time lags (τ = 2 and 15 s). Each of these panels have markers (yellow) superimposed to symbolize the motion of the particles, indicating: (A and D) static motion (solitary yellow rings), (B and C) constant velocity (identical arrows), (E) anisotropic diffusion and flow (double arrows with the longer arrows indicating flow direction along the adhesion mask’s semimajor axis), and (F) dispersed velocities (arrows of variable length representing a distribution of particle speeds). For each panel, data (in red and cyan) represent initial and final configurations, respectively. (White) Areas of overlap between features in the superposition. Scale bars are 5 μm for the image series and 1 μm for the CFs.
