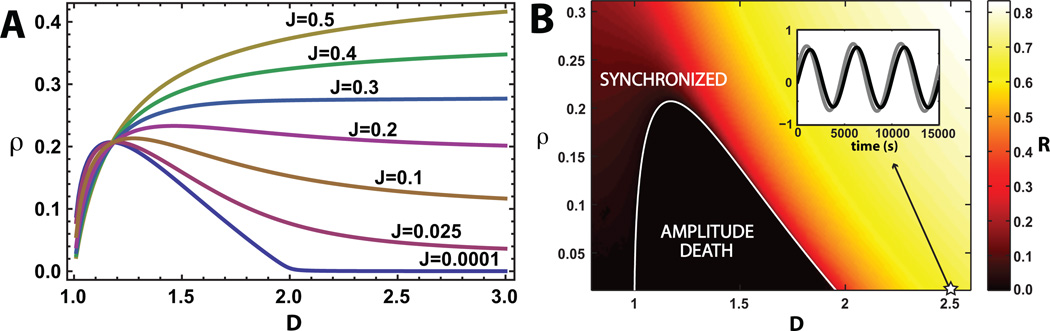
Figure 2.

(A) Phase boundaries for homogeneous oscillators. Phase boundary between the amplitude death phase and the synchronized phase in the ρ vs. D plane for various values of J, with ω₀ = 1 and λ₀ = 1. The synchronized phase occurs above the phase boundary and the amplitude death phase occurs below the boundary. (B) Numerical simulations for J = 0 with N = 40 identical oscillators with random initial conditions. Heat map of the steady-state amplitude of collective oscillations, R = |Z|, showing the transition from the amplitude phase to synchronized oscillations for D > 1. The white curve is the analytic phase boundary. Since J = 0, the phase transition occurs because of slow dynamics of the external medium at low-densities. Inset: Real part of z and Z during low density oscillations showing ~ 1000-fold slowing of oscillations relative to the uncoupled frequency ω₀ = 1s⁻¹ at the starred point (D = 2.5, ρ = 0.001, J = 0).