A dynamic investigation of the burst fracture process using a combined experimental and finite element approach

Abstract

Spinal burst fractures account for about 15% of spinal injuries and, because of their predominance in the younger population, there are large associated social and healthcare costs. Although several experimental studies have investigated the burst fracture process, little work has been undertaken using computational methods. The aim of this study was to develop a finite element model of the fracture process and, in combination with experimental data, gain a better understanding of the fracture event and mechanism of injury. Experimental tests were undertaken to simulate the burst fracture process in a bovine spine model. After impact, each specimen was dissected and the severity of fracture assessed. Two of the specimens tested at the highest impact rate were also dynamically filmed during the impact. A finite element model, based on CT data of an experimental specimen, was constructed and appropriate high strain rate material properties assigned to each component. Dynamic validation was undertaken by comparison with high-speed video data of an experimental impact. The model was used to determine the mechanism of fracture and the postfracture impact of the bony fragment onto the spinal cord. The dissection of the experimental specimens showed burst fractures of increasing severity with increasing impact energy. The finite element model demonstrated that a high tensile strain region was generated in the posterior of the vertebral body due to the interaction of the articular processes. The region of highest strain corresponded well with the experimental specimens. A second simulation was used to analyse the fragment projection into the spinal canal following fracture. The results showed that the posterior longitudinal ligament became stretched and at higher energies the spinal cord and the dura mater were compressed by the fragment. These structures deformed to a maximum level before forcing the fragment back towards the vertebral body. The final position of the fragment did not therefore represent the maximum dynamic canal occlusion.

Introduction

Spinal cord injuries (SCI) account for more than 10,000 admissions and 80,000 hospital bed-days in England each year [9]. Burst fractures are a relatively common cause of SCI in the younger population and account for about 15% of all spinal fractures [8]. Although there is a large cost associated with such injuries due to healthcare and loss of working hours, the most effective form of patient management is still in debate [2]. Decompressive surgery has been advocated when the level of occlusion seen on imaging of the spinal canal is greater than a prescribed level [7]. However, recent experimental evidence suggests that the final bone fragment position does not indicate the maximum dynamic occlusion that occurs at the moment of impact, and is a poor predictor of the level of neurological deficit or recovery [5, 15].

Due to the high rate of axial loading required to generate burst fractures, laboratory measurements are limited. To preserve the structural integrity of the specimens, the placement of transducers is restricted and the short time span of the event precludes other methods of measurement such as fluoroscopy and computed tomography.

Computational models avoid many of the restrictions of experimental studies and provide three-dimensional displacement and stress–strain data that would not be possible to obtain experimentally. Their use in analysing the burst fracture process has, however, been limited. Shirado [18] created a two-vertebra finite element model and compared the results under axial load with in vitro tests on human and bovine samples. The author demonstrated that the regions of maximum stress in the model corresponded with the fracture surfaces seen experimentally. Bozic et al. [3] modelled a cervical vertebra under uniform axial displacement applied through spring elements. The stresses produced were compared with bone strengths and the initiation of fracture was found to occur in the central region of the vertebral body. A similar method was used by Silva et al. [19]. None of the models used in trauma analysis have been developed to the level of those used in static analysis. In particular, no authors have attempted to model the spine at high rates of loading by using high strain rate material properties. The computational models used to study the burst fracture process have also not included the facet joints, whose interaction during impact may have significant influence on the stress fields developed. Further, validation has been undertaken only by comparison of the computed fracture sites with those observed experimentally after the fracture event has taken place, and no attempt has been made to carry out dynamic validation.

The aim of this study was to produce a finite element model capable of simulating the burst fracture process and, in combination with experimental data, to gain a greater insight into the fracture event.

Materials and methods

Experimental model

The experimental test set-up has been previously described [24]. Briefly, a rig was used to create burst fractures in three-vertebra bovine specimens by means of a drop weight. The specimens were prepared by removing the spinal cord and stripping paravertebral muscle to allow the vertebrae and discs to be observed. During the impact, the specimens were filmed with high-speed video (Kodak 4540; Roper Scientific, CA, USA) running at 4,500 frames/s. One camera was set up to view the outside of the specimen in the anterior–posterior plane whilst a second was used to film the inside of the spinal canal via a mirror. The video frames of the outside of the specimen were analysed using image analysis software (Image Pro Plus; Media Cybernetics, MD, USA). Key locations at the vertebra/disc interfaces were determined on every frame to give the vertical displacement at each time interval. The outermost positions of the intervertebral discs were also determined to give disc-bulge versus time data. For the purpose of this study, the video footage from two experimental specimens was analysed; the first was used to provide data for the determination of the disc properties and the second was used for the validation of the model. Both tests were carried out with an impact energy of 140 J.

After each impact test, the specimens were removed from the rig and dissected. A total of 27 specimens was analysed, the fractures were classified according to the Denis scale [8] and the mass of the vertebral body and fractured fragments was also measured.

Finite element model

Mesh generation

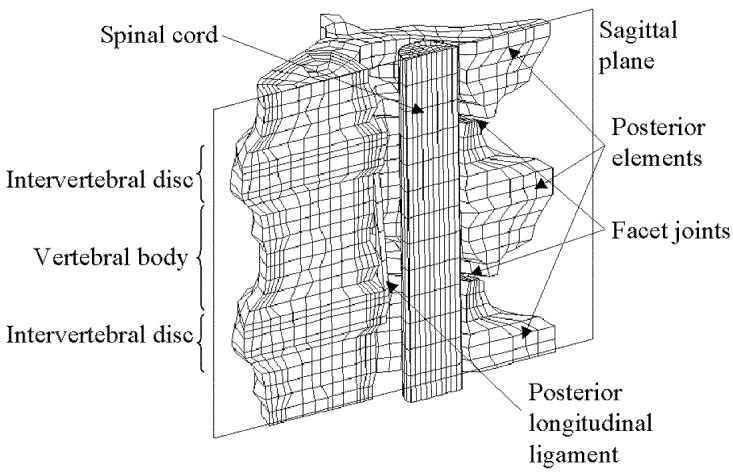
The finite element model was based on the preimpact CT scan of a specimen used in the experimental tests. The digitised images were downloaded to an image processing package (Image Pro Plus) and an inbuilt edge-detection algorithm was used to locate the interfaces between the different material components on each image. To reduce the computational expense, symmetry was assumed about the sagittal plane and only one half of each image was used. Principal nodes were manually assigned to one of the images and an algorithm was written to distribute a series of intermediate nodes between them. The co-ordinates of the principal nodes were superimposed onto the adjacent frame and manually realigned with the appropriate edges. The intermediate nodes were automatically redistributed. This process was repeated from frame to frame until nodes had been assigned to every plane. Eight-noded solid elements were then created from the nodal structure. In the region of the facet joints, intermediate layers were added to produce smaller elements and a smoother interface between the surfaces. The final model consisted of 4,462 nodes and 3,013 elements (Fig. 1). Appropriate constraints were applied to the inferior and sagittal surfaces of the model. A velocity–time curve was assigned to nodes on the superior surface using data from the high-speed video images of a 140-J impact.

Fig. 1.

Finite element mesh of the vertebral segment

Simulation

All processing was carried out using an explicit finite element code (LS-Dyna; Livermore Software Technology, CA, USA) running on a 128-MB Silicon Graphics workstation. Postprocessing was carried out using a three-dimensional visualisation package (D3 Plot; Oasys, London, UK).

Continuous simulation beyond initial fracture was not possible due to the large deformations of many of the material elements, causing errors in the computation. A second simulation of the fragment projection was therefore carried out by freezing the elemental deformations at the predicted point of fracture. Previous high-speed video data of the interior of the spinal canal [24] were then used to apply an appropriate transverse velocity to the bone fragment. The impact of the fragment onto the spinal canal could then be simulated with the surrounding structures in the deformed position. This was particularly important in the case of the posterior longitudinal ligament (PLL), where the degree of tension or laxity at the time the fragment was projected would have a substantial effect on its displacement.

Material properties

The mechanical properties of the component materials used in the finite element model are given in Table 1. Care was taken to find properties most appropriate to the large strains and strain rates to which the materials would be subjected.

Table 1.

Mechanical properties of the spinal components used in the finite element model

Material	Material model and properties				References
Trabecular bone	Plastic kinematic				[12]
	E=2.2 GPa
	ν=0.2
	Yield stress=42 MPa
Cortical bone	Plastic kinematic				[13]
	E=21 GPa
	ν=0.3
	Yield stress=132 MPa				[4]
Annulus fibrosus	Orthotropic elastic				[20] + experimental data
	Err=0.112 GPa	Eθθ=0.081 GPa		Ezz=0.072 GPa
	νzθ=0.626	νrz=0.023		νθr=0.021
Nucleus pulposus	Elastic fluid				[14]
	K=1.667 GPa
Cartilaginous endplate	Elastic				[27]
	E=25 MPa
	ν=0.4
Posterior longitudinal ligament	Piecewise linear plasticity				[21, 6]
	Preload=14% strain
	Strain		Stress (MPa)
	0		0
	0.11		2.04
	0.34		16.20
	0.44		20.80
Spinal cord	Elastic				[1]
	E=1.3 MPa
	ν=0.35
Dura mater	Anisotropic elastic				[25]
	Err=142 MPa	Eθθ=142 MPa		Ezz=0.7 MPa

In the case of the bony elements, a large variability in the postyield stress–strain characteristics has been found experimentally, even between specimens from the same species [11]. Therefore, a simple elastic-perfectly plastic model was used for both trabecular and cortical bone.

For the trabecular bone, the mean dry apparent density of samples taken from the experimental specimens (0.474 g/cm³) was used to calculate the elastic modulus and ultimate strength. The equations determined by Linde et al. [12] were used since these were considered to be the most accurate at high strain rates where the presence of marrow becomes significant. Because the strain rate within the trabecular region was not known, an iterative process was undertaken to determine the most appropriate value of the elastic modulus. An initial value of the strain rate was estimated and the corresponding modulus calculated and applied to the material property list in the analysis input file. The model was processed up to 1.5 ms and the average strain rate in the trabecular region determined. If the difference between this value and the estimated value was greater than 5%, the process was repeated with a revised estimate of the strain rate.

For cortical bone, the elastic modulus has been shown to vary with type [13], so properties for juvenile plexiform type were chosen to most closely match the experimental specimens.

The annulus fibrosus was modelled as an anisotropic elastic solid using the method developed by Spilker et al. [20] with a single set of material constants used to represent the composite of fibres and matrix in three orthotropic directions. The values obtained by Spilker et al. were determined under quasi-static loading. However, Race et al. [16] have shown that the disc properties are strain rate dependent. Due to the lack of data at high strain rates, it was necessary to compare the simulated deformation with that obtained from the high-speed video images and adjust the properties until good agreement was reached. It was assumed that the ratio of the moduli remained constant, and the magnitudes of all of the moduli were changed by the same proportion at each iteration. For each iteration, the simulated annulus strain was determined at time intervals of 0.22 ms, corresponding to the period between frames on the high-speed video. The mean and 95% confidence limits of the difference between the simulated strain and measured strain were then calculated. After four iterations, the mean error was 0.0047, corresponding to a longitudinal modulus of 0.72 MPa. The 95% confidence range of the error was lower than the estimated error in the video-measured strain due to the pixel size (±0.04) and hence this stiffness level was used in the model.

For the PLL, a preload of 3.883 MPa, equivalent to a strain of 14%, was applied to represent the strain in the ligament in the neutral position [21].

Validation

The simulated displacements of the upper disc, upper endplate and vertebra were compared with those obtained from the high-speed video. These positions were chosen since they were the most readily identifiable on the high-speed video images. Comparisons were made over the first 1.78 ms, at which time the total displacement of the model was 5.2 mm. In all cases there was good agreement (Fig. 2) with the mean difference being less than the maximum error in the video-measured displacement due to the pixel size (±0.42 mm). The zero difference fell within the 95% confidence levels of the two sets of data. For the disc bulge, the mean difference between the two sets of data was 0.40 mm, comparable with the estimated error on the high-speed video measurements due to the pixel size. Due to the small size of the displacements, the video-measured displacement could only be determined in relatively large step sizes and consequently the 95% confidence limits on the mean difference were large (−0.27 to 1.07 mm).

Fig. 2a–c.

Comparison of displacements in the experimental specimen, measured with high-speed video (right) and the finite element model (left) at times 0.0 (a), 0.67 (b) and 1.33 ms (c)

Results

Experimental model

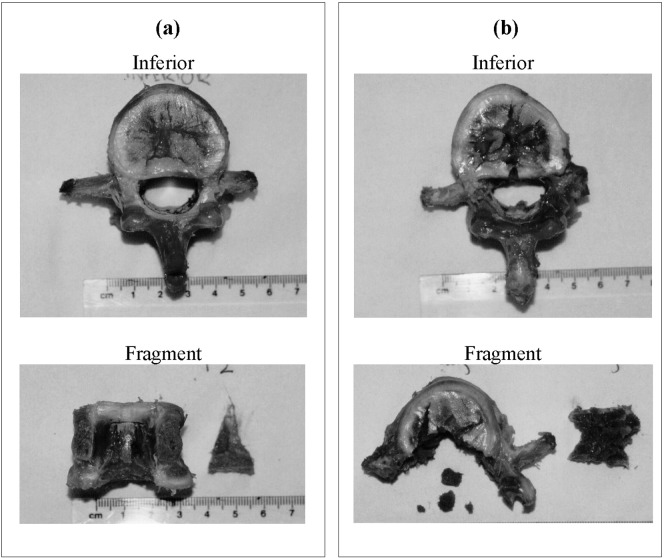
From the external camera images, the transverse processes were seen to rotate during impact at high energies. Some cracking of the posterior region of the vertebral body was also observed. Specimen dissection showed damage corresponding to the classic burst fracture pattern described by Denis [8] (Fig. 3). At the lowest impact energy (20 J), no or minimal cracking of the vertebra was observed. At medium impact energies, Denis type C fractures were seen with a wedge-shaped bone fragment attached to the endplate cartilage. At impact energies above 100 J, type A fractures were increasingly found, with the hourglass-shaped fragment extending from one endplate to the other. There was a positive correlation between the impact energy and the mass of the fragment or fragments (r=0.708, P<0.001). Even at the highest impact energy, the PLL always remained intact.

Fig. 3a, b.

Dissection of the specimens showing the inferior of the central vertebra and the dissected fragment. The specimens were impacted with energies of a 60 J producing a Denis type C fracture with a wedge-shape fragment and b 140 J producing a type A fracture with an hourglass-shaped fragment

Finite element model

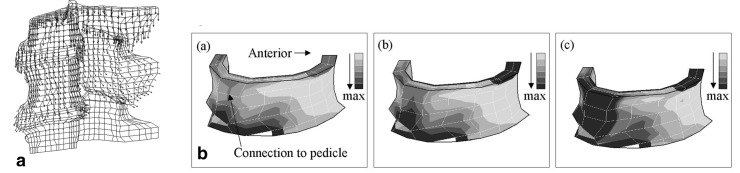
Due to the strain rate dependent characteristics of several of the component materials, only one impact energy (140 J) was considered using the velocity profile obtained from the experimental results as the input boundary condition. From the deformed shape plots, it could be seen that as the segment compressed, the inferior articular process was forced downwards and to the posterior of the connecting superior articular process (Fig. 4a). This caused the transverse process to rotate, as was also observed in the video footage. The motion of the processes produced a tensile force in the pedicle and generated localised regions of high tensile strain where the pedicle joined the posterior of the vertebral body (Fig. 4b), and extending in towards the centre of the body. Comparison of the elements displaying the highest tensile strain in the finite element model with the position of the fracture in the dissected specimens from the 140 J impact group showed good qualitative agreement.

Fig. 4 a.

Magnitude and direction of the nodal displacements in the finite element model at 0.89 ms after impact, showing the relative motions of the articular processes. b Maximum principal strain in the cortical shell at times 0.22 (a), 0.89 (b) and 1.56 ms (c). Darker shades indicate higher strains. The greatest region of strain is in the region where the pedicle (not shown) joins the vertebral body

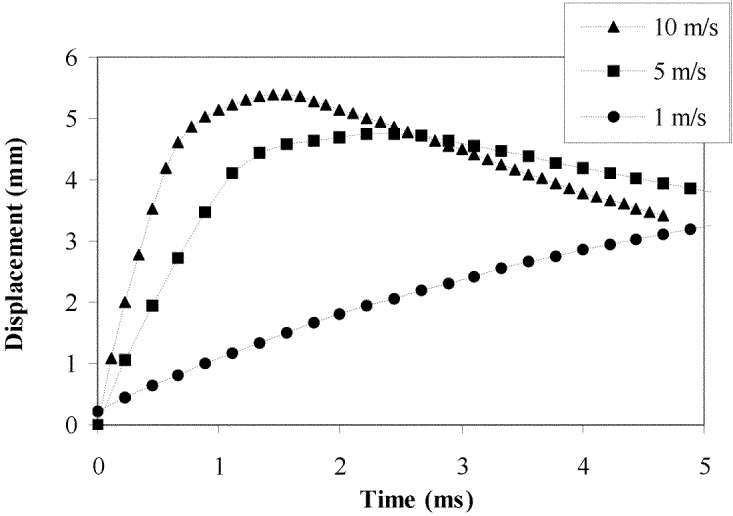
Analysis of the fragment projection into the spinal canal was carried out using a series of initial fragment velocities to encompass the range observed in the experimental tests. The results showed that the fragment stretched the PLL, initially slack due to the axial compression of the specimen. The stretched PLL then caused the fragment to be recoiled back towards the vertebral body. At high fragment velocities, the cord and dura mater became compressed before also acting to recoil the fragment back towards the vertebral body (Fig. 5).

Fig. 5.

Predicted fragment displacement into the spinal canal from the finite element model with different initial fragment velocities

Discussion

Although several experimental studies have measured dynamic spinal canal occlusion during the burst fracture process, the specimen geometry and short time period of the impact restrict transducer placement and the measurements that can be taken. Due to the rapid changes in the properties of spinal cord tissue after death, experimental models have removed the cord and surrounding tissue from the specimen prior to testing. By combining the results that are possible experimentally with those from a finite element model, this study has allowed a greater understanding of the fracture process to be achieved. In particular, this approach has enabled the internal relative motions and resultant strains of the component parts to be studied and the likely mechanism of fracture to be determined.

Validity of model

Calf spines were used in this study since they could be harvested from a narrow age range providing less variability than would have been possible with human specimens. The calf spine has been shown to exhibit similar mechanical responses to the human spine under a range of loading conditions [26] and the fracture patterns that were produced corresponded well with those observed in clinical practice.

The finite element model was developed specifically for analysing the spine under high-rate loading and care was taken in selecting the material properties most appropriate to high strain rates. In the case of the annulus fibrosus, data in the literature were not available and the properties had to be tuned to the experimental observations. In the case of the trabecular bone, a single phase continuum model was used, based on the properties of the tissue including the interstitial fluid at the average strain rate across the material. Recent studies have used poroelastic models for the vertebral body [23]. This method would allow the structure to be evaluated at different loading rates and may also enable a continuous simulation including both fracture initiation and expulsion of the fragment. Such a model should therefore be used in future studies.

Once optimised for one test, the model was validated against displacement data from a separate impact and good agreement was found. It is possible that the internal responses of the experimental and computational models were different whilst their external responses appeared similar. However, the risk was reduced by comparing the displacements of each component individually rather than studying only the overall displacement of the system. Further, in the case of the disc, where there was significant lateral bulge, the displacement in two different directions was studied. Although the comparison was limited to a single specimen, the process of dynamic validation marks a step change from previous studies that have relied purely on comparing the computed fracture sites with those observed experimentally at relatively low strain rates [18].

Fracture initiation

The burst fracture was so named by Holdsworth [10] because of the way the vertebral body appeared to have exploded from within. The mechanism by which fracture occurs has been the subject of some debate. Roaf [17] and Tran et al. [22] suggested that the increased pressure in the nucleus pulposus caused the endplates to bulge and crack, forcing nucleus material into the vertebral body at a greater rate than the contents of the body could be expelled. The results of the finite element study appear to contradict this, with the disc bulge greater in the transverse direction than into the endplates. Since the external disc bulge prediction from the finite element model could be validated with the high-speed video data, it would appear that the same mechanism occurred in the experimental tests. If this were the case, then it would seem likely that the fracture occurred in the reverse order to that previously proposed, with the vertebral body fracturing first. The subsequent expulsion of bone and fluid from the body into the canal would reduce the support offered to the endplates and continuing compression would then cause them to crack, as was observed in dissection. The model did, however, display an increased hoop stress around the cortex during compression, a phenomenon that Tran et al. [22] postulated was the cause of fracture. They suggested that the geometry of the cortical shell was responsible for the failure always occurring in the posterior region of the vertebral body. However, the finite element results indicate that another mechanism plays a greater role in causing this event, namely the interaction of the articular processes, which causes a tensile force to be transmitted through the pedicles, producing localised regions of high tensile strain in the posterior aspect of the vertebral body. Although experimental validation of this mechanism was not possible, both the finite element model and the experimental model exhibited the rotation of the transverse processes caused by the motion of the articular processes. The position of the highest tensile strains in the finite element model also appeared to correspond with the fracture sites seen in the dissected experimental specimens.

The combined results of the two simulations show good agreement with the high-speed video occlusion measurements. They indicate that the initial occlusion of the canal is caused by disc bulge, demonstrating why even non-fractured spines showed some occlusion on the video [24]. The secondary impact by the fragment was large enough to cause significant occlusion of the spinal cord, likely to be the point at which neurological damage would occur. After this, the action of the spinal cord and PLL force the fragment back towards the vertebral body. This is in agreement with the experimental tests [5, 15, 24] in demonstrating that the fragment resting position does not represent the greatest dynamic occlusion that occurs at the moment of impact. The final position alone is not therefore a suitable indication for decompressive surgery.

Summary

The results of the experimental and computational models suggest that the mechanism of burst fracture is as follows:

1. The high rate axial impact causes the inferior articular processes to be forced downwards and to the posterior of the connecting superior articular processes.

2. The twisting of the processes causes a tensile force to be transmitted through the pedicles to the posterior region of the vertebral body.

3. Fracture occurs in the posterior region of the vertebral body producing a wedge-shaped fragment of bone.

4. The fragment is projected into the spinal canal, stretching the PLL and compressing the spinal cord.

5. The action of the spinal cord and longitudinal ligament force the fragment back towards the vertebral body where it comes to rest.