Figure 2.

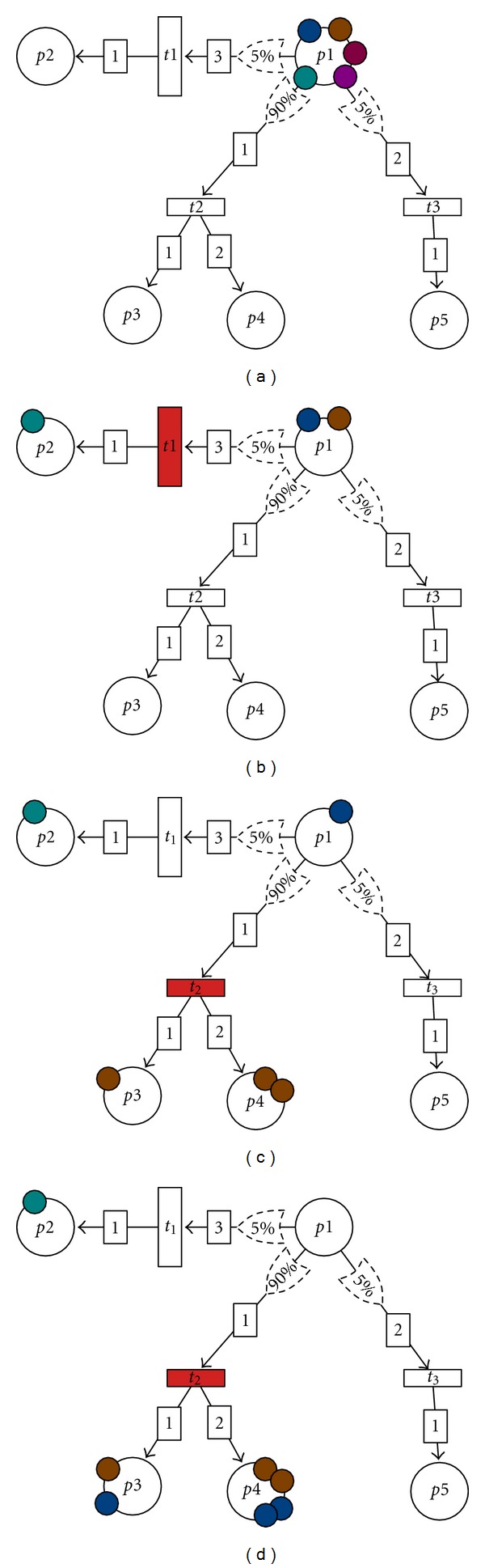
Illustration of the dynamics of a Flux Petri Net (FPN). (a) depicts the initial state of the FPN, while (b)–(d) depict its states after three transitions have been fired. This FPN comprises five places (p1–p5) and three transitions (t1–t3). The transition t1 consumes three tokens of p1, produces one token of p2, and has an associated flux distribution of 5%. Similarly, transition t2 consumes one token of p1, produces one token of p3, two tokens of p4, and has an associated flux of 90%. In the initial state (a), the place p1 contains five tokens, colored differently to be distinguishable. Since t1 requires three tokens of p1, t2 requires one token of p1, t3 two tokens of p1; that p1 contains five tokens; the three transitions t1, t2, and t3 are enabled in this configuration. The corresponding probabilities for each transition are P(t1) = 5/(5 + 90 + 5) = 0.05,  P(t2) = 90/(5 + 90 + 5) = 0.90  and  P(t3) = 5/(5 + 90 + 5) = 0.05. Suppose we select t1 with probability 0.05, then three tokens of p1 are consumed and one token of p2 is produced through t1. In the second state (b), only t2 and t3 are enabled, since the required number of tokens for t1 in p1 is not satisfied. This time, the respective probabilities associated with t2 and t3 are given by  P(t2) = 90/(90 + 5) = 0.948,  and P(t3) = 5/(90 + 5) = 0.052. Suppose t2 is selected, it consumes one token of p1 and produces one token of p3 and two of p4. In the third state (c), only transition t1 is enabled, and the FPN reaches a state (d) after firing t1 where no transition is enabled.