Segmentation of Brain Images Using Adaptive Atlases with Application to Ventriculomegaly

Abstract

Segmentation of brain images often requires a statistical atlas for providing prior information about the spatial position of different structures. A major limitation of atlas-based segmentation algorithms is their deficiency in analyzing brains that have a large deviation from the population used in the construction of the atlas. We present an expectation-maximization framework based on a Dirichlet distribution to adapt a statistical atlas to the underlying subject. Our model combines anatomical priors with the subject’s own anatomy, resulting in a subject specific atlas which we call an “adaptive atlas”. The generation of this adaptive atlas does not require the subject to have an anatomy similar to that of the atlas population, nor does it rely on the availability of an ensemble of similar images. The proposed method shows a significant improvement over current segmentation approaches when applied to subjects with severe ventriculomegaly, where the anatomy deviates significantly from the atlas population. Furthermore, high levels of accuracy are maintained when the method is applied to subjects with healthy anatomy.

1 Introduction

Automated algorithms for the segmentation of magnetic resonance (MR) brain images provide valuable tools for analyzing human brain structure. The incorporation of prior information is often required in many of these algorithms. One of the most commonly used types of prior information are statistical atlases that use a selection of training examples (i.e. manual delineations) from multiple subjects to model the spatial variability of the structures of interest [1, 22, 8, 17, 2]. These atlases can be utilized within a Bayesian framework to guide the algorithm as to where a structure is likely to appear within the image. Such approaches offer several advantages, including enhanced stability and convergence, as well as providing the ability to distinguish between structures with similar intensities. However, one of the major drawbacks of algorithms that use such statistical atlases is their inability to accurately model subjects whose brain anatomy deviates from the atlas population to a great extent. In some diseases and neurodegenerative conditions such as hydrocephalus, large changes take place in the geometry of the brain, potentially resulting in wildly inaccurate segmentations when using atlases derived from healthy populations.

Few methods have been proposed to effectively employ spatial atlases when population-specific training data is unavailable. Bhatia et al. [3] proposed a combined segmentation-registration method for atlas based brain segmentation in a group of subjects that are anatomically different from the atlas subjects. Riklin-Raviv et al. [19] avoided the use of a statistical atlas by introducing latent atlases generated from an image ensemble. The main limitation of these approaches is their dependency on the existence of a group of images that implicitly are needed to represent similar anatomy. Liu et al. utilize a generative segmentation model combined with a discriminative classifier to reduce dependency on an atlas [10]. However, this method focused on diseases that possess relatively modest geometric changes in brain structure.

Our approach for the segmentation of MR brain images is based on Gaussian Mixture Models (GMMs), similar to many other approaches (cf. [1, 22]). In GMMs, the intensity values of each cluster are assumed to have a Gaussian distribution whose parameters can be estimated by maximum likelihood (ML) using the expectation maximization (EM) algorithm [6]. The mixing coefficients of the GMM in brain segmentation algorithms can be given by a statistical atlas registered to the image space [22]. Consequently, if the difference between the subject and the training data used in the construction of the atlas can not be captured by the registration algorithm, these algorithms are unable to generate an accurate segmentation (Fig. 1). In other image processing applications, several approaches have been introduced to derive the mixing coefficients from the image itself. The concept of spatially varying mixing coefficients was first introduced by Sanjay-Gopal and Hebert [20]. In their work, a Gibss MRF-based prior was assumed on the mixing coefficients whose maximum a posteriori (MAP) estimates were computed by means of a generalized EM algorithm. Several other approaches have been proposed based on this model(see [12, 13]). Although these approaches are not biased to a statistical atlas, they can not effectively model separate structures with similar intensity values, such as sulcal and ventricular cerebrospinal fluid (CSF). This is a major advantage of methods employing a statistical atlas.

Fig. 1.

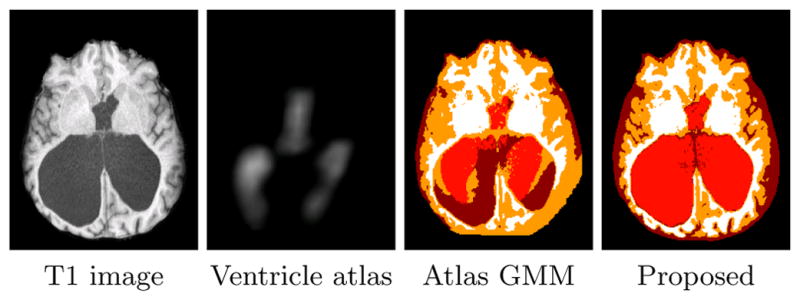
Results of an atlas-based GMM segmentation algorithm on a subject with large ventricles (sulcal-CSF, ventricles, GM, and WM are represented by dark red, light red, orange, and white, respectively).

In this work, we propose a new framework that combines the desirable properties of both of these models. We model the mixing coefficients by a Dirichlet distribution whose parameters are derived from a statistical atlas of healthy subjects. Employing this model within an EM framework, we estimate an “adaptive” atlas which is updated iteratively by combining the original statistical atlas with information from the image under study. Since the adaptive atlas is informed by a statistical atlas, clusters with similar intensities can be embedded in our adaptive atlas. At the same time, the influence of the data on the adaptive atlas removes the bias toward the statistical atlas to a great extent. The resulting adaptive atlas is specific to the subject and therefore, does not limit the atlas based segmentation of the image. Unlike the approaches of [3, 19], our model does not require an ensemble of images and automatically adapts the statistical atlas to a single subject. It is worth mentioning that two recent works have incorporated a Dirichlet model in image segmentation algorithms in a different context [13, 11].

We test and validate our method both on subjects with normal brain anatomy and subjects suffering from hydrocephalus. Hydrocephalus patients can have severe ventriculomegaly which are not well modeled by statistical atlases generated from normal subjects. Because of the specific interest in ventricular size and shape in hydrocephalus patients [18, 4], traditional three-class brain segmentation approaches are not appropriate. For this application, we employ a four tissue class model, consisting of gray matter (GM), white matter (WM), sulcal CSF, and ventricular CSF. Our results demonstrate that our method applied to brains with severe ventriculomegaly has superior performance over state-of-the-art atlas-based methods, while it achieves similar accuracy in the segmentation of brains with normal anatomy.

2 Methods

In this section, we first review the Gaussian mixture model (GMM) with spatially varying mixing coefficients introduced in [20] before presenting our work on incorporating adaptive atlases in the segmentation of brain MR images. In a standard atlas approach, the mixing coefficients represent our atlas, providing the prior probability that a tissue class occurs at a voxel. The central idea of this paper is to employ a Dirichlet distribution as a prior to the mixing coefficients, where the mode of the distribution is given by a statistical atlas constructed from healthy subjects. In so doing, the estimated mixing coefficients can deviate significantly from the original statistical atlas and adapt to the subject data.

2.1 Gaussian mixture model with spatially varying mixing coefficients

Our goal is to segment the brain into K structures. We assume that the intensity distribution of each structure follows a Gaussian distribution. Hence the observed MR image(s) can be modeled by a GMM. Let x_j be the Cx1 vector of the observed intensities where j ∈ {1, 2, …, N} represents the voxel location in the image and C represents the number of input channels. Also let θ_k = {μ_k, Σ_k} be the parameters of the Gaussian distribution associated with structure k (k ∈ {1, 2, …, K}). Here, μ_k is the Cx1 mean vector and Σ_k is the CxC covariance matrix.

The label of each voxel j is denoted by a Kx1 vector z_j. If voxel j belongs to structure k, z_j = e_k where e_k is a Kx1 vector whose kth component is 1 and all of its other components are 0. We model the prior distribution of z_j’s as a multinomial distribution with the Kx1 vector parameter π_j, i.e. f (z_jk = 1) = π_jk where the second letter in the subscript denotes the vector component index. The π_jk’s are called the mixing coefficients of GMM and they represent the possibility that voxel j belongs to structure k a priori (by construction, ${\sum }_{k=1}^K{\pi }_{jk}=1,\forall j$). With the assumption of the independence of z_j’s, we can write the prior on z = (z₁, z₂, …, z_N) as:

$$f(\mathbf{z})=\prod _{j=1}^N\prod _{k=1}^K{\pi }_{jk}^{z_{jk}}.$$ (1)

In [20], it was assumed that the observations x_j’s are independent, hence the conditional distribution of the complete data y = (x₁, x₂, …, x_N, z₁, z₂, …, z_N) is given by:

$$f(\mathbf{y}\mid \mathbf{\Psi })=\prod _{j=1}^N\prod _{k=1}^K{[{\pi }_{jk}G({\mathbf{x}}_j;{\theta }_k)]}^{z_{jk}},$$ (2)

where Ψ = (π₁, π₂, …, π_K, θ₁, θ₂, …, θ_K) and G(,; θ_k) is a Gaussian distribution with parameter θ_k. Sanjay-Gopal and Hebert derived an EM algorithm for ML estimation of the Gaussian parameters θ_k’s and π_jk’s in (2):

$$w_{jk}=\frac{{\pi }_{jk}G({\mathbf{x}}_j;{\theta }_k)}{{\sum }_{l=1}^K{\pi }_{jl}G({\mathbf{x}}_j;{\theta }_l)}$$ (3)

$${\pi }_{jk}=w_{jk},{\mu }_k=\frac{{\sum }_{j=1}^N{w}_{jk}{\mathbf{x}}_j}{{\sum }_{j=1}^N{w}_{jk}},{\mathbf{\sum }}_k=\frac{{\sum }_{j=1}^N{w}_{jk}({\mathbf{x}}_j-{\mu }_k){({\mathbf{x}}_j-{\mu }_k)}^T}{{\sum }_{j=1}^N{w}_{jk}}$$ (4)

The posterior probabilities given by (3) are used to associate each voxel to one of the structures by choosing the one that has the largest posterior probability w_jk.

It is worth mentioning here that the two other common assumptions on π_jk’s are:

1. π_jk = π_k, ∀j, which is the classical mixture model approach.

2. π_jk = p_jk, where p_jk is given by a statistical atlas and ${\sum }_{k=1}^K{p}_{jk}=1,\forall j$.

2.2 GMM with adaptive atlases

A major drawback of using (2) in the segmentation of the brain structures is the insufficiency of this model in distinguishing structures with similar intensities from one another. Assumption (ii) in the previous section resolves this problem to some extent. However, if the underlying image largely differs from the subjects used in the construction of the atlas, this assumption hinders the correct segmentation of the image. Here we describe a MAP framework to solve this limitation of atlas-based segmentation algorithms.

To incorporate a statistical atlas within a framework that estimates the mixing coefficients based on the subject data, we treat π_j as a random vector with a distribution whose parameters are derived from the statistical atlas. As the vector π_j lives on a K-dimensional simplex, we should choose a distribution with simplex support as a prior on π_j. The natural choice for such a distribution is a Dirichlet distribution:

$$\mathit{Dir}({\pi }_j;{\alpha }_j)=\frac{{\prod }_{k=1}^K{\pi }_{jk}^{({\alpha }_{jk}-1)}}{B({\alpha }_j)},$$ (5)

where B(_·) is a Beta function and α_j is the Kx1 vector parameter of the distribution. In our model, we have a statistical atlas generated from training data p_jk, that provides us the a priori probability of a structure j occurring at voxel k in a healthy population (as will be described later in Sec 2.4). We therefore employ a Dirichlet prior with parameter α_jk = 1 + δp_jk, ∀k. The parameter δ is non-negative and we describe its selection later in this section. For the case of δ = 1, the values p_j = (p_j,1, p_j;2, …, p_j,K) represent the mode of the Dirichlet prior probability function.

As the brain structures often form a connected region, we incorporate a Markov Random Field (MRF) as a prior on z_j’s. In this work, we utilize a model similar to the one employed in [22, 16], which yields the following prior on z:

$$f(\mathbf{z}\mid \pi )=\frac{1}{Z_{\mathit{MRF}}}\prod _{j=1}^N\prod _{k=1}^K{\pi }_{jk}^{z_{jk}}\mathit{exp}(-\beta \sum _{i\in N_j}\sum _{l=1,l\ne k}^K{z}_{jk}{z}_{il}),$$ (6)

where π = (π₁, π₂, …, π_N), N_j is the 6-connected neighborhood of voxel j, β is the parameter controlling the effect of the prior, and Z_MRF is the normalizing factor. It is worth mentioning that we assume uniform prior on θ_k’s.

With these assumptions, the conditional distribution of the complete data in our model is given by:

$$f(\mathbf{y}\mid \mathbf{\Psi })=\frac{1}{Z_{\mathit{MRF}}}\prod _{j=1}^N\prod _{k=1}^K{({\pi }_{jk}G({\mathbf{x}}_j;{\theta }_k))}^{z_{jk}}\mathit{exp}(-\beta \sum _{i\in N_j}\sum _{l=1,l\ne k}^K{z}_{jk}{z}_{il})$$ (7)

2.3 Estimation Algorithm

In this section we derive the estimation algorithm for the parameters in (7) using a generalized EM algorithm. The EM algorithm is an iterative approach for the estimation of model parameters that involves two steps: (i) an E-step in which, given the parameter estimates from the previous iteration, the conditional expectation of the complete data likelihood function is computed; and (ii) a M-step in which the new estimate of the model parameters is computed to increase or maximize the conditional expectation computed in E-step [6]. We provide here the E-step and M-step for (7). If Ψ^(t) is the set of estimated parameters from iteration t, then we have:

E-Step

$$Q(\mathbf{\Psi }\mid {\mathbf{\Psi }}^{(t)})=E\left\{lnf(\mathbf{y}\mid \mathbf{\Psi })\mid \mathbf{x},{\mathbf{\Psi }}^{(t)}\right\}+lnf(\pi ,{\theta }_1,{\theta }_2,\dots ,{\theta }_K)$$ (8)

The main component in (8) is computing $w_{jk}^{(t)}=E\{z_{jk}\mid \mathbf{x},{\mathbf{\Psi }}^{(t)}\}$. Due to the MRF prior on z, computing $w_{jk}^{(t)}$ analytically is computationally intractable. Using a mean field approximation yields (see [16]):

$$\begin{array}{r}{w}_{jk}^{(t)}=E\left\{z_{jk}\mid \mathbf{x},{\mathbf{\Psi }}^{(t)}\right\}\approx E\left\{z_{jk}\mid \mathbf{x},{\mathbf{\Psi }}^{(t)},E\{{\mathbf{z}}_i\},i\in N_j\right\}\\ =f\left\{z_{jk}=1\mid \mathbf{x},{\mathbf{\Psi }}^{(t)},E\{{\mathbf{z}}_i\},i\in N_j\right\}\\ =\frac{f(\mathbf{x}\mid z_{jk}=1,{\mathbf{\Psi }}^{(t)})f(z_{jk}=1\mid E\{{\mathbf{z}}_i\},i\in N_j)}{{\sum }_{k=1}^{K}f(\mathbf{x}\mid z_{jk}=1,{\mathbf{\Psi }}^{(t)})f(z_{jk}=1\mid E\{{\mathbf{z}}_i\},i\in N_j)}.\end{array}$$ (9)

M-step

In this step, we want to find the set of parameters Ψ^(t+1) that maximizes (8). This can be done independently for ${\pi }_j^{(t+1)}$ and ${\theta }_k^{(t+1)}$. For ${\theta }_k^{(t+1)}$, we first derive the equation for ${\mu }_k^{(t+1)}$ and then for ${\mathbf{\sum }}_k^{(t+1)}$. As we assume uniform priors on θ_k’s, the solution for ${\theta }_k^{(t+1)}$is similar to (4):

$${\mu }_k^{(t+1)}=\frac{{\sum }_{j=1}^N{w}_{jk}^{(t)}{\mathbf{x}}_j}{{\sum }_{j=1}^N{w}_{jk}^{(t)}},{\mathbf{\sum }}_k^{(t+1)}=\frac{{\sum }_{j=1}^N{w}_{jk}^{(t)}({\mathbf{x}}_j-{\mu }_k^{(t+1)}){({\mathbf{x}}_j-{\mu }_k^{(t+1)})}^T}{{\sum }_{j=1}^N{w}_{jk}^{(t)}}$$ (10)

Because of the constraint on π_jk’s, we use Lagrange multiplier to maximize (8) with respect to π_jk:

$${\frac{\partial }{\partial {\pi }_{jk}}\{Q(\mathbf{\Psi }\mid {\mathbf{\Psi }}^{(t)})+\lambda (1-\sum _{k=1}^K{\pi }_{jk})\}|}_{{\pi }_{jk}^{(t+1)}}={\frac{\partial }{\partial {\pi }_{jk}}\left\{\left(\delta p_{jk}+w_{jk}^{(t)}\right)ln{\pi }_{jk}-\lambda {\pi }_{jk}\right\}|}_{{\pi }_{jk}^{(t+1)}}=0.$$ (11)

Hence:

$${\pi }_{jk}^{(t+1)}=\frac{\delta p_{jk}+w_{jk}^{(t)}}{\lambda }.$$ (12)

Using the constraint on π_jk’s and p_jk’s and (9) λ is given by:

$$\lambda =\sum _{k=1}^K\delta p_{jk}+\sum _{k=1}^K{w}_{jk}^{(t)}=\delta +1.$$ (13)

Therefore the update for ${\pi }_{jk}^{(t+1)}$ is given by:

$${\pi }_{jk}^{(t+1)}=\frac{\delta p_{jk}+w_{jk}^{(t)}}{\delta +1}.$$ (14)

The statistical atlas, by construction, should be a smooth probability map that represents the population under study. Although p_jk’s are given by a smooth statistical atlas, w_jk’s do not have this desirable smooth property. To enforce the spatial smoothness on w_jk’s and make the mixing coefficients reffective of a population that the subject is drawn from, we convolve w_jk’s with a spatial Gaussian kernel in (14):

$${\pi }_{jk}^{(t+1)}\approx (1-\kappa )p_{jk}+\kappa (G\ast w_{jk}^{(t)}),$$ (15)

where G is a Gaussian kernel (we used a kernel size of 2.5 mm in all our experiments). This provides our model for generating the adaptive atlas. Although the Gaussian filtering deviates from our statistical framework, simple smoothing of parameter estimates has previously been shown to offer good convergence properties and computational advantages over explicit smoothing priors when used within the EM algorithm [14].

Eq. (15) has an intuitive interpretation of being a weighted average of the original atlas with the subject atlas. We call $\kappa =\frac{1}{\delta +1}$ in (15) the adaptation factor, which controls the influence of the image on the adaptive atlas. For instance, k = 0 results in case (ii) of Sec 2.1 (a non-adapted statistical atlas), whereas k = 1 results in a smooth version of (4) (no influence from the statistical atlas). In particular, k = 0.5, which we used in all our experiments, enforces the mode of the Dirichlet prior on π_j to be equal to p_j. Fig. 2 shows how the adaptive atlas changes during the segmentation algorithm.

Fig. 2.

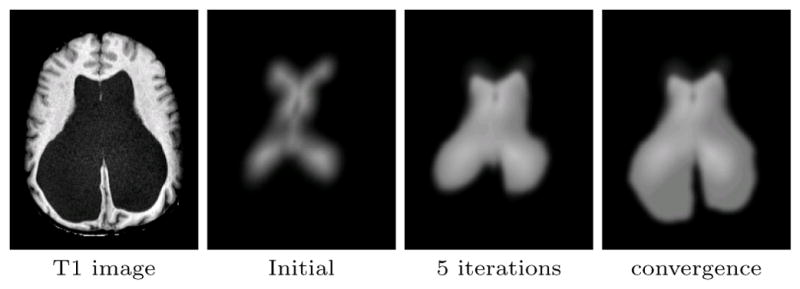
Evolution of the adaptive atlas from the initial statistical atlas. It originally is biased by the training data but eventually converges to the subject’s geometry.

2.4 Implementation Details

Statistical atlas

The statistical atlas we used in this work is built from a set of 18 manual delineations of the structures of interest, based on the IBSR data set [23]. For each image in the atlas, the delineation is rigidly aligned with the current atlas image, and a smooth approximation of the probabilities is accumulated. The smoothing replaces the step edge at the boundary of each structure in their binary delineation by a linear ramp over a band of size ε (which we set to 10 mm in our work) [2]. In this work, the statistical atlas contains prior information for sulcal-CSF, ventricles, GM, and WM, however it can be easily extended to more structures.

Atlas registration

The statistical atlas needs to be registered to the image space for the segmentation task. We used a joint segmentation and registration technique that alternates between estimating the segmentation given the current atlas position, and then updating the transformation given the current segmentation. The registration maximizes the correlation of the mixing coefficients with the posterior probabilities. The transformation is updated at each iteration of the algorithm. We used affine transformations in this work.

Initializing the EM algorithm

To initialize the intensity centroids of the different structures, we first estimate the robust minimum and maximum of the intensity (the intensity values at 5% and 95% of the histogram, respectively), and normalize the profiles such that 0 corresponds to the minimum and 1 to the maximum. We then initialized the centroids to empirically determined values stemming from the expected intensities of the tissue classes for the appropriate pulse sequence.

Convergence criteria

We used the maximum amount of change in posterior probabilities as the measure of convergence of the EM algorithm. We set a threshold of 0.01 on this maximum in our work.

3 Experiments

We evaluated the performance of the introduced method on both brains with healthy anatomy and hydrocephalus brains which suffer from ventriculomegaly. We compared the performance of our method to an in-house implementation of a standard atlas-based EM segmentation algorithm (which we refer to as the atlas EM segmentation algorithm in this section). The only difference between this implementation and our proposed method lies in the use of a conventional statistical atlas instead of the introduced adaptive atlas. Brain images were preprocessed to extract the brain and correct for inhomogeneities. Some manual refinement of the brain mask was necessary on some cases. We also compared the performance of our method in the segmentation of the ventricles of hydrocephalus brains with the Freesurfer software [8], which employs a nonstationary MRF model and a probabilistic atlas updated using nonlinear registration. Finally we compared our method to a registration based segmentation algorithm which uses Hammer [21], a state-of-the-art deformable registration algorithm, to label the ventricles. We used Dice overlap coefficient [7] and false negative ratio (for the ventricle segmentation experiment) between the automated segmentation and the ground truth as the accuracy measures.

3.1 Normal Brains

To study the performance of the algorithm on brains with normal anatomy, we used both simulated and real data sets. In our first experiment, we used the simulated T1 brain from the Brainweb phantom [5] with 3% noise and no inhomogeneity. As Brainweb truth model does not have a separate segmentation for the ventricles, we manually separated the sulcal-CSF from the ventricles on the ground truth image. As Table 1 demonstrates, our method has slightly better overall accuracy in segmenting the simulated brain in comparison to the non-adaptive EM segmentation algorithm.

Table 1.

Comparison of the non-adaptive EM segmentation algorithm and the proposed method on brains with normal anatomy (Brainweb and IBSR data sets), measured by Dice overlap coefficient. For IBSR data set, the mean dice value over 10 subjects is reported.

	Brainweb				IBSR*
Algorithm	CSF	VENT	GM	WM	VENT	GM	WM
Atlas EM	0.938	0.953	0.942	0.952	0.851	0.931	0.877
Adaptive atlas	0.945	0.957	0.945	0.951	0.835	0.933	0.878

In the second experiment, we used the IBSR database [23] which contains MR brain images of 18 real subjects. As we also use this database to create our statistical atlas, we separated the subjects to two non-overlapping groups of 8 and 10 subjects. We used the first group to create the statistical atlas and then used that atlas to validate the algorithms on the 10 other subjects. As the manual segmentation of this data set does not contain sulcal-CSF and includes it inside the GM segmentation, we combined the sulcal-CSF and GM labels in the automated segmentation results before comparing to the manual segmentation. The accuracy of our method and the non-adaptive atlas EM segmentation algorithm in the segmentation of this data set are very similar (Table 1).

3.2 Brains with ventriculomegaly

The main advantage of our approach using the adaptive atlases over other atlas-based segmentation algorithms is its ability in the segmentation of images that largely deviate from the atlas population. To study this unique aspect of our adaptive method, we evaluated the performance of the proposed method, the atlas EM segmentation algorithm, Freesurfer, and Hammer on the segmentation of ventricles of 14 patients with hydrocephalus. Our data set has 9 subjects with moderate and 5 subjects with marked ventricular dilatation, as diagnosed by a neuroradiologist. This allows us to be able to study the effect of large deviations from the atlas population on the performance of each algorithm more thoroughly. Also, in addition to Dice overlap coefficient, we computed the false negative ratio ( $\text{FNR}=\frac{\mid \mathit{Ref}\mid -\mid \mathit{Ref}\cap \mathit{Seg}\mid }{\mid \mathit{Ref}\mid }$) between the automatically segmented ventricles (Seg) and the manual delineation by an expert (Ref) for each method. We found FNR very informative in our validation, as the errors in the segmentation of the ventricles in this data set are mostly due to a misclassification as other structures.

The validation results (Table 2) show that our method has superior accuracy on all the subjects in comparison to other methods. As expected, the atlas EM segmentation algorithm, Freesurfer, and the Hammer based segmentation perform significantly worse on subjects with marked ventriculomegaly, whereas the performance of our approach is not altered significantly by the amount of the dilatation. Freesurfer failed (did not complete or resulted in a nearly empty image) in the processing of 3 subjects with severe structural anomalies due to problems in its brain extraction step. We also note that Freesurfer attempts to segment a much larger number of structures and is therefore at a disadvantage trying to solve a more difficult problem. Also it is worth mentioning that for the approach based on Hammer, we first used FANTASM [15] to classify the image voxels as CSF, GM, or WM. We then used the atlas provided with the Hammer software [9] to segment the ventricles. Although this atlas contains 101 regions of interest, we grouped all of these regions into sulcal-CSF, ventricles, GM, and WM in our experiments.

Table 2.

Segmentation accuracy measures on hydrocephalus data set.

Subject	Dice overlap coefficient				False negative ratio
	Atlas EM	Freesurfer	Hammer	Adaptive	Atlas EM	Freesurfer	Hammer	Adaptive
Moderate 1	0.908	0.884	0.786	0.977	0.151	0.156	0.320	0.015
Moderate 2	0.964	0.929	0.889	0.972	0.050	0.053	0.154	0.038
Moderate 3	0.961	0.930	0.864	0.967	0.040	0.043	0.187	0.023
Moderate 4	0.959	0.911	0.827	0.970	0.056	0.061	0.251	0.026
Moderate 5	0.953	0.889	0.824	0.962	0.051	0.108	0.236	0.030
Moderate 6	0.941	0.890	0.847	0.949	0.063	0.083	0.203	0.035
Moderate 7	0.898	0.753	0.864	0.970	0.163	0.362	0.194	0.026
Moderate 8	0.937	0.923	0.860	0.958	0.106	0.065	0.191	0.073
Moderate 9	0.951	0.922	0.576	0.977	0.080	0.079	0.580	0.022
Mean	0.941	0.892	0.815	0.967	0.084	0.112	0.257	0.032
Marked 1	0.496	Failed*	0.119	0.977	0.670	Failed*	0.936	0.043
Marked 2	0.494	Failed*	0.154	0.962	0.671	Failed*	0.915	0.064
Marked 3	0.561	Failed*	0.111	0.967	0.608	Failed*	0.941	0.046
Marked 4	0.798	0.152	0.190	0.970	0.333	0.917	0.893	0.044
Marked 5	0.863	0.258	0.417	0.981	0.233	0.849	0.731	0.021
Mean	0.642	0.205	0.198	0.971	0.503	0.883	0.883	0.044
Mean (All)	0.835	0.767	0.595	0.968	0.234	0.252	0.481	0.036

^*Algorithm failed due to problems in the skull-stripping step.

Fig. 3 shows that even in the cases of moderate ventriculomegaly, the atlas EM segmentation algorithm, Freesurfer and Hammer are not able to segment the ventricles as accurately as the adaptive approach.

Fig. 3.

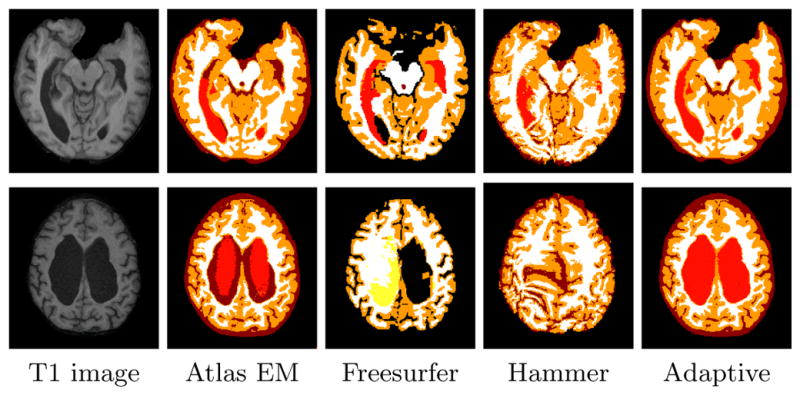
Comparison of the adaptive atlas approach and three other atlas-based segmentation algorithms on hydrocephalus subjects with moderate (top row) and marked (bottom row) ventriculomegaly(sulcal-CSF, ventricles, GM, and WM are represented by dark red, light red, orange, and white, respectively. Yellow represents WM-hypointenisty in Freesurfer segmentation).

4 Discussion

We have presented a new statistical framework for the atlas based segmentation of MR brain images based on adaptive atlases. Our approach addresses the segmentation of images that deviate from the atlas population to a great extent. The validation results confirm that our algorithm has a superior performance in the segmentation of such subjects, while maintaining high level of accuracy in the segmentation of brains with healthy anatomy. On the hydrocephalus data, our

method was shown to have some advantages when compared to a deformable registration approach (Hammer), as well as an atlas-based approach that employs deformable registration to update its atlas (Freesurfer). Deformable registration approaches are prone to local optima when the target is highly dissimilar from the template. Furthermore, the proposed approach leads to computationally e3-cient atlas updating (a Gaussian filter and simple averaging) when compared to deformable registration. The introduced adaptive atlas provides a general model for the computation of the mixing coefficients of a GMM model; for instance the conventional approach of using a statistical atlas as the mixing coefficients is a special case of this model. Although we described the adaptive atlas concept as part of a GMM model, our approach can be easily incorporated in other atlas-based probabilistic segmentation methods.

In computing the adaptive atlas, we included a smoothing step within EM iterations to make the adaptive atlas reffective of a population that the subject is drawn from. We will investigate explicitly modeling this property as a hierarchical prior on the mixing coefficients.