Abstract
The dissociative recombination of  has been an intriguing problem for more than half a century. The early experiments on
has been an intriguing problem for more than half a century. The early experiments on  during the first 20 years were carried out without mass analysis in decaying plasma afterglows, and thus the measured rates pertained to an uncontrolled mixture of
during the first 20 years were carried out without mass analysis in decaying plasma afterglows, and thus the measured rates pertained to an uncontrolled mixture of  and impurity ions. When mass analysis was used, the rate coefficient was determined to be an uneventful value of about 10−7 cm3 s−1, a very common rate coefficient for many molecular ions. But this was not the end of the story, not even the beginning of the end; it marked only the end of the beginning. The story I will tell in this article started about 10 years ago, when the dissociative recombination of
and impurity ions. When mass analysis was used, the rate coefficient was determined to be an uneventful value of about 10−7 cm3 s−1, a very common rate coefficient for many molecular ions. But this was not the end of the story, not even the beginning of the end; it marked only the end of the beginning. The story I will tell in this article started about 10 years ago, when the dissociative recombination of  was approaching its deepest crisis. Today, owing to an extensive experimental and theoretical effort, the state of affairs has reached a historically unique level of harmony, although there still remains many things to sort out.
was approaching its deepest crisis. Today, owing to an extensive experimental and theoretical effort, the state of affairs has reached a historically unique level of harmony, although there still remains many things to sort out.
Keywords: recombination, dissociation, Jahn–Teller, electron capture
1. Introduction
This 10 years retrospective on the dissociative recombination of  is of course related to the fact that the first Royal Society Discussion Meeting (RSDM) on
is of course related to the fact that the first Royal Society Discussion Meeting (RSDM) on 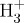 was held in the year 2000, i.e. just over 10 years ago. At that time, which is very clear from a reading of my summary of the situation concerning experimental and, to some extent, theoretical studies of the dissociative recombination of
was held in the year 2000, i.e. just over 10 years ago. At that time, which is very clear from a reading of my summary of the situation concerning experimental and, to some extent, theoretical studies of the dissociative recombination of  [1], the situation was bewildering. The reaction itself appears, naively, to be very simple:
[1], the situation was bewildering. The reaction itself appears, naively, to be very simple:
| 1.1 |
Only three protons and three electrons, of which one electron is free before the reaction and all electrons are bound after the reaction, at the expense of a complete or partial break-up of a stable molecular ion.
At the first RSDM, one can summarize the situation as follows.
— There was consensus that the rate coefficient (ke) at an electron temperature of 300 K as measured in ion storage rings was about 10−7 cm3 s−1 and that the
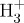 ions used in these experiments occupied only their zeroth vibrational level [1–5]; the preliminary results of Jensen et al. [4] and Kreckel et al. [5] were reported in [1] as ‘private communications’).
ions used in these experiments occupied only their zeroth vibrational level [1–5]; the preliminary results of Jensen et al. [4] and Kreckel et al. [5] were reported in [1] as ‘private communications’).— Theoretical calculations were unable to come anywhere close to the storage ring results [6], typically yielding two orders of magnitude lower rate coefficients. Theory had excluded the direct dissociative recombination mechanism through a favourable curve crossing already through the pioneering works by Kulander & Guest [7] and Michels & Hobbs [8], and the work by Orel et al. [6] clearly pointed towards an indirect mechanism dominated by bound Rydberg states. This made
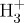 together with HeH+ [9,10] atypical ions in terms of dissociative recombination.
together with HeH+ [9,10] atypical ions in terms of dissociative recombination.— The monitoring of a decaying hydrogen plasma either by measurements of the
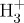 infrared spectrum [11] or by measurement of the electron density by a Langmuir probe in a stationary [12] or flowing afterglow [13–17] gave rate coefficients covering the stunning range from 1.8×10−7 to 10−11 cm3 s−1. The early theoretical estimate by Michels & Hobbs [8] no doubt had an influence on the interpretation of the afterglow results, and was sufficiently convincing as to leave even Bates in a state of uncertainty [18].
infrared spectrum [11] or by measurement of the electron density by a Langmuir probe in a stationary [12] or flowing afterglow [13–17] gave rate coefficients covering the stunning range from 1.8×10−7 to 10−11 cm3 s−1. The early theoretical estimate by Michels & Hobbs [8] no doubt had an influence on the interpretation of the afterglow results, and was sufficiently convincing as to leave even Bates in a state of uncertainty [18].— The observation of
 in diffuse interstellar clouds [19], where the ion is destroyed primarily by dissociative recombination, was difficult to reconcile with a rate coefficient of the order of 10−7 cm3 s−1 [20].
in diffuse interstellar clouds [19], where the ion is destroyed primarily by dissociative recombination, was difficult to reconcile with a rate coefficient of the order of 10−7 cm3 s−1 [20].— Measurements of isotopologues of
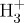 by different techniques also presented a confusing picture.
by different techniques also presented a confusing picture.— Essentially nothing was known about a possible rotational dependence of the rate coefficient.
2. The clouds are gathering
If the situation was confusing during the first RSDM, it would get worse. First out were new measurements by means of the stationary afterglow technique [21]. The paper was submitted about six months after the first RSDM on 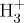 and thus not included even as a personal communication in the review of recombination rate coefficients [1]. It was surprising in several respects. It represented a revival of the stationary afterglow technique, which had not been used since 1984 [12] to study the dissociative recombination of
and thus not included even as a personal communication in the review of recombination rate coefficients [1]. It was surprising in several respects. It represented a revival of the stationary afterglow technique, which had not been used since 1984 [12] to study the dissociative recombination of 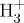 . Groups involved in afterglow measurements had, by the turn of the millennium, migrated to the flowing afterglow technique. More surprising, however, was that the measured rate coefficient, less than or equal to 1.3×10−8 cm3 s−1, was about a factor of 10 lower than the one measured by Macdonald et al. [12]. Glosik et al. [21] pointed out the excellent agreement with the flowing afterglow/Langmuir probe result obtained by Smith & Spanel [15], but, surprisingly, offered no explanation as to why their result differed so much from a result obtained with a very similar stationary afterglow technique [12]. However, it was clear that Glosik et al.’s low rate coefficient was difficult to refute.
. Groups involved in afterglow measurements had, by the turn of the millennium, migrated to the flowing afterglow technique. More surprising, however, was that the measured rate coefficient, less than or equal to 1.3×10−8 cm3 s−1, was about a factor of 10 lower than the one measured by Macdonald et al. [12]. Glosik et al. [21] pointed out the excellent agreement with the flowing afterglow/Langmuir probe result obtained by Smith & Spanel [15], but, surprisingly, offered no explanation as to why their result differed so much from a result obtained with a very similar stationary afterglow technique [12]. However, it was clear that Glosik et al.’s low rate coefficient was difficult to refute.
During the same time, it became clear that the rotational temperature in the ion storage ring experiments needed to be addressed. At CRYRING in Stockholm, several experiments using different ion source conditions in a hollow cathode source were performed during the spring of 2001 and presented at the symposium on dissociative recombination in connection with the American Chemical Society meeting in Chicago in August 2001 [22]. The rate coefficient depended on the ion source conditions (pressure, gas mixture), and hence, probably, on the rotational distribution, but the experiment was not well characterized and many questions remained, one of them obviously being: is it possible that the rate coefficient decreases radically when the rotational temperature is decreased?
The Chicago meeting also included a presentation by Glosik and co-workers [23], in which the recombination rate coefficient for  was lowered to less than 3×10−9 cm3 s−1. Figure 1 shows the recombination rate coefficient as a function of the D2 density (for some reason, it was the D2 density curve which was shown; however, an essentially identical curve was recorded for H2) in the stationary afterglow experiment taken from Plasil et al. [23]. This figure was to play the key role during the coming years in Glosik’s arguing for a very low, maybe negligible, recombination rate coefficient for
was lowered to less than 3×10−9 cm3 s−1. Figure 1 shows the recombination rate coefficient as a function of the D2 density (for some reason, it was the D2 density curve which was shown; however, an essentially identical curve was recorded for H2) in the stationary afterglow experiment taken from Plasil et al. [23]. This figure was to play the key role during the coming years in Glosik’s arguing for a very low, maybe negligible, recombination rate coefficient for 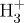 and
and 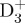 . The argument was that H2 (and D2) contributed to the deionization process at densities above 1011 cm−3 by three-body collisions by stabilizing the electron-capture process:
. The argument was that H2 (and D2) contributed to the deionization process at densities above 1011 cm−3 by three-body collisions by stabilizing the electron-capture process:
| 2.1 |
Not only did this explain, according to Glosik, the very low binary (in the absence of H2) recombination rate coefficient, it also explained why other afterglow experiments gave higher values; these experiments [16,17] had been carried out at H2 densities where the three-body effect had saturated. To the best of my recollection, none of the afterglow researchers present at Glosik’s presentation publically objected to his interpretation.
Figure 1.
Recombination of  and the dependence of the observed effective rate coefficient (αeff) on the H2 density. The measurements in the stationary afterglow apparatus were performed at various helium pressures in the range of 1.5–3 Torr and at several Ar densities (indicated on the x-axis). The He temperature was 260±40 K. The crosses indicate error bars. Results from Laubé et al [17], Gougousi et al. [16], Amano [11] and Canosa et al. [14] are included. Adapted from Plasil et al. [23].
and the dependence of the observed effective rate coefficient (αeff) on the H2 density. The measurements in the stationary afterglow apparatus were performed at various helium pressures in the range of 1.5–3 Torr and at several Ar densities (indicated on the x-axis). The He temperature was 260±40 K. The crosses indicate error bars. Results from Laubé et al [17], Gougousi et al. [16], Amano [11] and Canosa et al. [14] are included. Adapted from Plasil et al. [23].
The Chicago meeting also witnessed a presentation of a new theoretical calculation by Greene et al. [24], which included a new mechanism based on the Jahn–Teller coupling [25]. Their preliminary results were a factor of 10 smaller than the storage ring results and in agreement with Glosik’s afterglow results [21]. Kokoouline et al. [26] published their results in Nature, and the letter to Nature was followed by a ‘New and Views’ by Suzor-Weiner & Schneider [27] who remarked (concerning rotational excitations) that: ‘Moreover, the effect should increase for rotationally hot  target ions, perhaps explaining the larger value measured ion storage ring experiments’ (p. 872).
target ions, perhaps explaining the larger value measured ion storage ring experiments’ (p. 872).
McCall & Oka [28], p. 370 pointed out that a low recombination rate was straight-forward to reconcile with the observation of 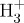 in diffuse interstellar clouds:
in diffuse interstellar clouds:
perhaps ke [assuming a rate coefficient of about 10−7 cm3 s−1] is wrong, in which case the cosmic-ray flux and electron fraction in diffuse clouds are what we expect them to be. But perhaps the current value of ke is correct! Then there is exciting new astrophysics waiting to be explored… either carbon is mostly not ionized in diffuse clouds or the cosmic-ray flux is much higher than generally thought.
Given the confusing situation in 2001 regarding the rate of recombination of 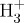 and its important astrophysical implications, Oka’s cry for help [29] is understandable! But the clouds would soon disperse.
and its important astrophysical implications, Oka’s cry for help [29] is understandable! But the clouds would soon disperse.
3. The clouds are dispersing
The  community responded vigorously to the challenge, and the next 5 years saw the most intense activity, experimental and theoretical, in trying to solve the riddle with the dissociative recombination of
community responded vigorously to the challenge, and the next 5 years saw the most intense activity, experimental and theoretical, in trying to solve the riddle with the dissociative recombination of  . At the second RSDM on
. At the second RSDM on  , Oka cautiously noted that it seemed like the results from ion storage ring experiments and theoretical calculations were converging [30].
, Oka cautiously noted that it seemed like the results from ion storage ring experiments and theoretical calculations were converging [30].
In the proceedings of the Chicago meeting, one can note some optimism in the contribution by Larsson et al. [22], who are even (concerning preliminary results from June 2001) talking about ‘… a breakthrough in the experimental study of the DR [dissociative recombination]  …’ (p. 90). In fact, the CRYRING team was on the wrong track and it was not until it joined forces with the Saykally group at UC Berkeley that the breakthrough would emerge [31–33]. A supersonic expansion ion source was built and characterized at Berkeley, shipped to Stockholm and CRYRING for preliminary tests, shipped back to Berkeley for modifications and finally shipped back to Stockholm for experiments. The characterization of the rotational temperature of the
…’ (p. 90). In fact, the CRYRING team was on the wrong track and it was not until it joined forces with the Saykally group at UC Berkeley that the breakthrough would emerge [31–33]. A supersonic expansion ion source was built and characterized at Berkeley, shipped to Stockholm and CRYRING for preliminary tests, shipped back to Berkeley for modifications and finally shipped back to Stockholm for experiments. The characterization of the rotational temperature of the 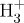 ions extracted from the ion source by means of cavity-ring-down spectroscopy showed that the ions were rotationally cold. The experiments at CRYRING gave a much more structured cross section than was obtained in earlier experiments, thus showing that the ions were colder than in any previous experiment [31–33].
ions extracted from the ion source by means of cavity-ring-down spectroscopy showed that the ions were rotationally cold. The experiments at CRYRING gave a much more structured cross section than was obtained in earlier experiments, thus showing that the ions were colder than in any previous experiment [31–33].
In any type of experimental physics endeavour, it is highly desirable that experimental results from one experiment are reproduced by another, completely independent, experiment. The efforts at TSR in Heidelberg, which had been proceeding in parallel with those at CRYRING for quite some time, were to play a decisive role. Kreckel et al. [5], in their experiments measuring the 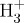 vibrational distribution as a function of storage time in TSR, had noted that their data were best fitted when a substantial rotational energy, 0.3 eV, in the
vibrational distribution as a function of storage time in TSR, had noted that their data were best fitted when a substantial rotational energy, 0.3 eV, in the  ions was assumed. Lammich et al. [34] carried out extensive experiments on the isotopologue D2H+ and found that the cross section depended on the degree of rotational excitation. The TSR team now pushed for an elegant solution to the problem of rotational excitations. They used a 22-pole radio-frequency ion trap cooled to 10 K as injector to the storage ring, and used the ultracold (0.5 meV transverse energy spread) as a target in the recombination experiments. Instead of reproducing the final results published by Kreckel et al. [35], the preliminary results, distributed to the
ions was assumed. Lammich et al. [34] carried out extensive experiments on the isotopologue D2H+ and found that the cross section depended on the degree of rotational excitation. The TSR team now pushed for an elegant solution to the problem of rotational excitations. They used a 22-pole radio-frequency ion trap cooled to 10 K as injector to the storage ring, and used the ultracold (0.5 meV transverse energy spread) as a target in the recombination experiments. Instead of reproducing the final results published by Kreckel et al. [35], the preliminary results, distributed to the 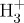 community in December 2004, are shown in figure 2 because it more immediately conveys the excitement we felt when we realized that the results from the two storage rings were in perfect agreement. It should be noted that the TSR result was not an absolute measurement but a relative one, normalized to the CRYRING result for high-energy peak at 10 eV. The small differences below 10 meV are entirely due to the small difference in electron temperature (see [36] for a detailed analysis of the electron temperature influence on the resolution in storage ring experiments). Recent experiments at the TSR gave absolute values in excellent agreement with the CRYRING results [37].
community in December 2004, are shown in figure 2 because it more immediately conveys the excitement we felt when we realized that the results from the two storage rings were in perfect agreement. It should be noted that the TSR result was not an absolute measurement but a relative one, normalized to the CRYRING result for high-energy peak at 10 eV. The small differences below 10 meV are entirely due to the small difference in electron temperature (see [36] for a detailed analysis of the electron temperature influence on the resolution in storage ring experiments). Recent experiments at the TSR gave absolute values in excellent agreement with the CRYRING results [37].
Figure 2.
Comparison of results for dissociative recombination of  . The black dots displays the preliminary results from TSR [35], and the grey line displays the results from CRYRING [31–[33]. The results on the y-axis are the rate coefficient measured in the merged electron and ion beams. The small difference between the experimental data of CRYRING and TSR is due to the colder electron beam used in the TSR experiment (see [36] for a detailed discussion of the resolution merged-beam experiments). (H. Kreckel 2004, personal communication).
. The black dots displays the preliminary results from TSR [35], and the grey line displays the results from CRYRING [31–[33]. The results on the y-axis are the rate coefficient measured in the merged electron and ion beams. The small difference between the experimental data of CRYRING and TSR is due to the colder electron beam used in the TSR experiment (see [36] for a detailed discussion of the resolution merged-beam experiments). (H. Kreckel 2004, personal communication).
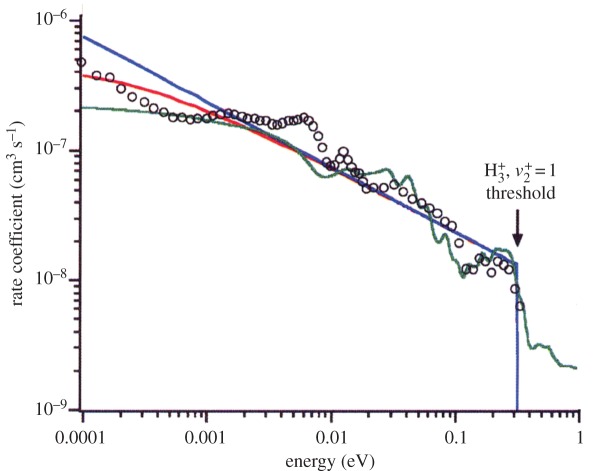
Already when the CRYRING experiments with the supersonic expansion source were ongoing, the CRYRING team had been informed by Greene that he and his collaborators had found a convention inconsistency in their calculations [26], which, when corrected, increased the cross section by a factor of π2, i.e. essentially a factor of ten. This brought the theoretical cross section in overall agreement with the storage ring results [38,39]. Later, Jungen & Pratt [40] would use a combined analytical and empirical approach to arrive at essentially the same result. Figure 3 illustrates the excellent agreement between experiment and theory.
Figure 3.
The rate coefficient (in a merged electron–ion beam with parameters from the TSR electron target) for dissociative recombination of  . Circles: experimental results from Kreckel et al. [35]; blue solid line: unconvolved theoretical results from Jungen & Pratt [40]; red solid line: theoretical results from Jungen & Pratt [40] convolved with the parameters for the electron target in TSR [35]; green solid line: convolved theoretical results from Fonseca dos Santos et al. [41]. Adapted from Jungen & Pratt [40].
. Circles: experimental results from Kreckel et al. [35]; blue solid line: unconvolved theoretical results from Jungen & Pratt [40]; red solid line: theoretical results from Jungen & Pratt [40] convolved with the parameters for the electron target in TSR [35]; green solid line: convolved theoretical results from Fonseca dos Santos et al. [41]. Adapted from Jungen & Pratt [40].
Meanwhile Glosik’s group launched a series of experiments using the stationary afterglow technique [42–44], and claimed that the negligible recombination rate coefficient (at low H2 density; figure 1) was in agreement with theory. This situation changed in 2003, with two publications [38,39]. The Glosik group also performed experiments using a flowing afterglow apparatus [45,46] and cavity-ring down absorption experiments [47–49]. The Glosik group slowly realized that upholding a very low binary recombination rate coefficient was difficult to reconcile with the very good agreement between theory and ion storage ring experiments. Johnsen [50] offered a speculative but plausible explanation of the peculiar H2 density dependence shown in figure 1; if  (v=1) recombined much slower than
(v=1) recombined much slower than 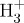 (v=0), incomplete vibrational quenching of the
(v=0), incomplete vibrational quenching of the 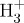 ions due to insufficient H2 density would leave many slowly recombining
ions due to insufficient H2 density would leave many slowly recombining 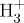 (v=1) ions in the plasma. The advantage with this hypothesis was that it could be tested theoretically, and this was done a few years later by Fonseca dos Santos et al. [41], who effectively falsified Johnsen’s hypothesis;
(v=1) ions in the plasma. The advantage with this hypothesis was that it could be tested theoretically, and this was done a few years later by Fonseca dos Santos et al. [41], who effectively falsified Johnsen’s hypothesis; 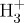 (v=1) recombines even faster than
(v=1) recombines even faster than  (v=0).
(v=0).
The next wave of publications from the Glosik group [51–56] focused on understanding the region above a D2 (H2) density of about 1012 cm−3 and concluded that the binary recombination rate coefficient was essentially in agreement with theory and the storage ring results. They were unable to explain the decrease in the rate coefficient below 1012 cm−3.
At the 8th International Conference on Dissociative Recombination: Theory, Experiments and Applications in Lake Tahoe in 2010, Johnsen [57] discussed the  plasma experiments in the Glosik group, and in their recent review of dissociative recombination of
plasma experiments in the Glosik group, and in their recent review of dissociative recombination of  , Johnsen & Guberman [58] proposed an explanation that appears both simple and reasonable. At
, Johnsen & Guberman [58] proposed an explanation that appears both simple and reasonable. At 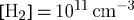 , they estimated that the time scale for production of
, they estimated that the time scale for production of 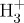 ions in the stationary afterglow experiment was 10 ms, whereas the time scale for destruction was 1 ms. Thus, the loss rate of electrons, which is the quantity measured in an afterglow experiment, was limited not by recombination but by the formation rate of the ions. I steer the reader to Johnsen & Guberman [58] for a critical analysis of all afterglow experiments on
ions in the stationary afterglow experiment was 10 ms, whereas the time scale for destruction was 1 ms. Thus, the loss rate of electrons, which is the quantity measured in an afterglow experiment, was limited not by recombination but by the formation rate of the ions. I steer the reader to Johnsen & Guberman [58] for a critical analysis of all afterglow experiments on 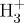 . Their conclusion was that there are no afterglow experiments supporting a recombination rate coefficient for
. Their conclusion was that there are no afterglow experiments supporting a recombination rate coefficient for  (v=0) significantly smaller that obtained in the storage rings.
(v=0) significantly smaller that obtained in the storage rings.
4. The isotopologues and nuclear spin effects
Kokoouline and co-workers [39,59] and Greene & Kokoouline [60] studied the isotopologues 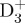 , D2H+ and H2D+ and found good agreement with the CRYRING results [61] for
, D2H+ and H2D+ and found good agreement with the CRYRING results [61] for 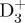 , fairly good agreement with the CRYRING results for H2D+ [62], and quite poor agreement with the TSR results for D2H+ [34]. The question that arose was whether the disagreement for D2H+ depended on a flawed experiment or problems with the theory. In order to test this, we performed experiments at CRYRING and obtained perfect agreement with the results from the TSR [63]. Pagani et al. [64] included new calculations by Kokoouline, which included more rovibrational states and also improved numerical treatment of symmetrization of rovibronic wave functions of D2H+, something that brought the results into better agreement with the experimental results.
, fairly good agreement with the CRYRING results for H2D+ [62], and quite poor agreement with the TSR results for D2H+ [34]. The question that arose was whether the disagreement for D2H+ depended on a flawed experiment or problems with the theory. In order to test this, we performed experiments at CRYRING and obtained perfect agreement with the results from the TSR [63]. Pagani et al. [64] included new calculations by Kokoouline, which included more rovibrational states and also improved numerical treatment of symmetrization of rovibronic wave functions of D2H+, something that brought the results into better agreement with the experimental results.
Kokoouline & Greene [39] initially found that ground state  recombines faster than
recombines faster than 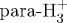 ; however, in more refined calculation, Fonseca dos Santos et al. [41] found a distinctly larger recombination cross section for
; however, in more refined calculation, Fonseca dos Santos et al. [41] found a distinctly larger recombination cross section for 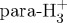 . Experiments at TSR [35] seemed to support this, although the difference in rate between para and ortho was much smaller, and subsequent experiments at TSR were non-conclusive [65]. Experiments at CRYRING in which highly enriched
. Experiments at TSR [35] seemed to support this, although the difference in rate between para and ortho was much smaller, and subsequent experiments at TSR were non-conclusive [65]. Experiments at CRYRING in which highly enriched 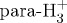 was used showed that
was used showed that 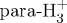 clearly recombined faster than
clearly recombined faster than  produced from normal H2 [66]. The ratio of the rate coefficients of pure
produced from normal H2 [66]. The ratio of the rate coefficients of pure 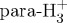 to pure
to pure  was determined to be approximately 2 at low collision energies, which is too small a ratio to make dissociative recombination the dominant process in determining the ortho/para ratio of
was determined to be approximately 2 at low collision energies, which is too small a ratio to make dissociative recombination the dominant process in determining the ortho/para ratio of  in the diffuse interstellar medium [66]. A more careful analysis has since then modified this statement, suggesting that the ortho/para
in the diffuse interstellar medium [66]. A more careful analysis has since then modified this statement, suggesting that the ortho/para 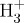 ratio is controlled by a competition between dissociative recombination and thermalization via reactive collisions with H2 [67].
ratio is controlled by a competition between dissociative recombination and thermalization via reactive collisions with H2 [67].
The para/ortho ratio has also been studied in the plasma afterglow [68,69], where a para/ortho rate coefficient ratio of approximately 10 or more if the error bars are taken into account was found at an electron temperature of 77 K, and Kokoouline and Greene’s theoretical ratio at 77 K was 2.6 [64].
5. Conclusions
I have attempted to describe some of the key advances in the study of the dissociative recombination of 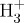 since the first RSDM on
since the first RSDM on  12 years ago. Space limitations have made it impossible to be comprehensive. A book chapter in the research monograph by Larsson & Orel [36], a feature article [70], and the recent review by Johnsen & Guberman [58] fill the gaps in this article, and the latter is in particular noteworthy for its critical analysis of the plasma afterglow experiments and the theory of dissociative recombination of
12 years ago. Space limitations have made it impossible to be comprehensive. A book chapter in the research monograph by Larsson & Orel [36], a feature article [70], and the recent review by Johnsen & Guberman [58] fill the gaps in this article, and the latter is in particular noteworthy for its critical analysis of the plasma afterglow experiments and the theory of dissociative recombination of  .
.
Major experimental and theoretical efforts during the past decade have brought the situation with  dissociative recombination to a reasonable degree of satisfaction. Although
dissociative recombination to a reasonable degree of satisfaction. Although 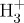 has been famous (or maybe infamous) for delivering surprises, it seems unlikely that there will be any major changes in the
has been famous (or maybe infamous) for delivering surprises, it seems unlikely that there will be any major changes in the  recombination framework. This does not, however, mean that there are no remaining question marks to iron out. Remaining questions are:
recombination framework. This does not, however, mean that there are no remaining question marks to iron out. Remaining questions are:
— the analysis of the plasma afterglow experiments has not yet been exhausted; and
— the finer details in the comparison of storage ring results and theory is not yet satisfactory. The resonances observed in the experiments at storage rings (figure 2) have a smaller amplitude than those calculated by theory. A possible explanation for this was put forward by Petrignani et al. [71], who, in a very careful and systematic study using different types of ion sources at the TSR, found that the rotational temperature experiments with storage rings claimed to have been carried out with cold ions (approx. 50 K) probably were done with ions having a rotational temperature around 300–400 K owing to poorly controlled heating mechanisms. The recombination rate coefficient’s dependence on the rotational quantum number is sufficiently small to render the effect to be of only minor astrophysical importance; however, it suggests the desirability to develop an in situ measurement of the ion temperature in a storage ring.
To me, there is nevertheless something a little sad about ending an article by concluding that the long and controversial story of the dissociative recombination of  is approaching its final chapter. It gives me the same slightly sad emotion as each time I have been watching Mozart’s Cosi fan tutte, his last great comic opera, and the curtain falls. Just as the belief that Mozart could have written another Cosi fan tutte if he had lived is a saddening thought, it is also a saddening thought to believe that
is approaching its final chapter. It gives me the same slightly sad emotion as each time I have been watching Mozart’s Cosi fan tutte, his last great comic opera, and the curtain falls. Just as the belief that Mozart could have written another Cosi fan tutte if he had lived is a saddening thought, it is also a saddening thought to believe that  cannot deliver yet another major surprise to its many friends. But maybe it can!
cannot deliver yet another major surprise to its many friends. But maybe it can!
Acknowledgements
I thank Richard Thomas, who did many experiments on  in CRYRING together with me and other collaborators, for valuable comments on the draft manuscript, Slava Kokoouline for pointing out the improved calculations on D2H+ and the referees for valuable comments. One of the referees wisely moderated my optimism, stemming from the bias of having lived through the darker periods of the
in CRYRING together with me and other collaborators, for valuable comments on the draft manuscript, Slava Kokoouline for pointing out the improved calculations on D2H+ and the referees for valuable comments. One of the referees wisely moderated my optimism, stemming from the bias of having lived through the darker periods of the 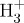 controversy.
controversy.
References
- 1.Larsson M. 2000. Experimental studies of the dissociative recombination of H3+. Phil. Trans. R. Soc. Lond. A 358, 2433–2444 10.1098/rsta.2000.0658 (doi:10.1098/rsta.2000.0658) [DOI] [Google Scholar]
- 2.Sundström G., et al. 1994. Destruction rate of H3+ by low energy electrons measured in a storage-ring experiment. Science 263, 785–787 10.1126/science.263.5148.785 (doi:10.1126/science.263.5148.785) [DOI] [PubMed] [Google Scholar]
- 3.Tanabe T., et al. 2000. Dissociative recombination at the TARN II storage ring. In Dissociative recombination: theory, experiment and applications IV (eds Larsson M., Mitchell J. B. A., Schneider I. F.), pp. 170–179 Singapore: World Scientific. [Google Scholar]
- 4.Jensen M. J., Pedersen H. B., Safvan C. P., Seirsen K., Urbain X., Andersen L. H. 2001. Dissociative recombination and excitation of H3+. Phys. Rev. A 63, 052701. 10.1103/PhysRevA.63.052701 (doi:10.1103/PhysRevA.63.052701) [DOI] [Google Scholar]
- 5.Kreckel H., et al. 2002. Vibrational and rotational cooling of H3+. Phys. Rev. A 66, 052509. 10.1103/PhysRevA.66.052509 (doi:10.1103/PhysRevA.66.052509) [DOI] [Google Scholar]
- 6.Orel A. E., Schneider I. F., Suzor-Weiner A. 2000. Dissociative recombination of H3+: progress in theory. Phil. Trans. R. Soc. Lond. A 358, 2445–2456 10.1098/rsta.2000.0659 (doi:10.1098/rsta.2000.0659) [DOI] [Google Scholar]
- 7.Kulander K. C., Guest M. F. 1979. Excited electronic states of H3 and their role in the dissociative recombination of H3+. J. Phys. B 12, L501–L504 10.1088/0022-3700/12/16/006 (doi:10.1088/0022-3700/12/16/006) [DOI] [Google Scholar]
- 8.Michels H. H., Hobbs R. H. 1984. Low-temperature dissociative recombination of e + H3+. Astrophys. J. 286, L27–L29 10.1086/184378 (doi:10.1086/184378) [DOI] [Google Scholar]
- 9.Guberman S. L. 1994. Dissociative recombination without a curve crossing. Phys. Rev. A 49, R4277–R4280 10.1103/PhysRevA.49.R4277 (doi:10.1103/PhysRevA.49.R4277) [DOI] [PubMed] [Google Scholar]
- 10.Sarpal B. K., Tennyson J., Morgan L. 1994. Dissociative recombination without a curve crossing. J. Phys. B 27, 5943–5953 10.1088/0953-4075/27/24/017 (doi:10.1088/0953-4075/27/24/017) [DOI] [Google Scholar]
- 11.Amano T. 1990. The dissociative recombination rate coefficient of H3+, HN2+ and HCO+. J. Chem. Phys. 92, 6492–6501 10.1063/1.458594 (doi:10.1063/1.458594) [DOI] [Google Scholar]
- 12.Macdonald J., Biondi M. A., Johnsen R. 1984. Recombination of electrons with H3+ and H5+. Planet. Space Sci. 32, 651–654 10.1016/0032-0633(84)90117-X (doi:10.1016/0032-0633(84)90117-X) [DOI] [Google Scholar]
- 13.Adams N. G., Smith D. 1987. Recent advances in the studies of reaction rates relevant to interstellar chemistry. In Astrochemistry, IAU Symp. 120 (eds Vardya M. S., Tarafdar S. P.), pp. 1–18 Dordrecht, The Netherlands: Reidel Publishing Company. [Google Scholar]
- 14.Canosa A., Gomet J. C., Rowe B. R., Mitchel J. B. A., Queffelec J. L. 1992. Further measurements of the H3+ (v = 0,1,2) dissociative recombination rate coefficient. J. Chem. Phys. 97, 1028–1037 10.1063/1.463282 (doi:10.1063/1.463282) [DOI] [Google Scholar]
- 15.Smith D., Spanel P. 1993. Dissociative recombination of H3+ and some other interstellar ions: a controversy resolved. Int. J. Mass Spectrom. Ion Proc. 129, 163–182 10.1016/0168-1176(93)87040-Y (doi:10.1016/0168-1176(93)87040-Y) [DOI] [Google Scholar]
- 16.Gougousi T., Johnsen R., Golde M. F. 1995. Recombination of H3+ and D3+ in a flowing afterglow plasma. Int. J. Mass Spectrom. Ion Proc. 149/150, 131–151 10.1016/0168-1176(95)04248-J (doi:10.1016/0168-1176(95)04248-J) [DOI] [Google Scholar]
- 17.Laubé S., Le Padellec A., Sidko O., Rebrion-Rowe C., Mitchell J. B. A., Rowe B. R. 1998. New FALP-MS measurements of H3+, D3+ and HCO+ dissociative recombination. J. Phys. B 31, 2111–2128 10.1088/0953-4075/31/9/023 (doi:10.1088/0953-4075/31/9/023) [DOI] [Google Scholar]
- 18.Bates D. R., Guest M. F., Kendall R. A. 1993. Enigma of H3+ dissociative recombination. Planet. Space Sci. 41, 9–15 10.1016/0032-0633(93)90011-P (doi:10.1016/0032-0633(93)90011-P) [DOI] [Google Scholar]
- 19.McCall B. J., Geballe T. R., Hinkle K. H., Oka T. 1998. Detection of H3+ in the diffuse interstellar medium towards Cygnus OB2 no. 12. Science 279, 1910–1913 10.1126/science.279.5358.1910 (doi:10.1126/science.279.5358.1910) [DOI] [PubMed] [Google Scholar]
- 20.Geballe T. R. 2000. H3+ between the stars. Phil. Trans. R. Soc. Lond. A 358, 2503–2513 10.1098/rsta.2000.0663 (doi:10.1098/rsta.2000.0663) [DOI] [Google Scholar]
- 21.Glosik J., Plasil R., Poterya V., Kudrna P., Tichy M. 2000. The recombination of H3+ ions with electrons: dependence of partial pressure of H2. Chem. Phys. Lett. 331, 209–214 10.1016/S0009-2614(00)01183-0 (doi:10.1016/S0009-2614(00)01183-0) [DOI] [Google Scholar]
- 22.Larsson M., et al. 2003. Studies of dissociative recombination in CRYRING. In Dissociative recombination of molecular ions with electrons (ed. Guberman S. L.), pp. 87–94 New York, NY: Kluwer/Plenum Publishers. [Google Scholar]
- 23.Plasil R., Glosik J., Poterya V., Kudrna P., Vicher M., Pysanenko A. 2003. Recombination of H3+ and D3+ with electrons. In Dissociative recombination of molecular ions with electrons (ed. Guberman S. L.), pp. 249–263 New York, NY: Kluwer/Plenum Publishers. [Google Scholar]
- 24.Greene C. H., Kokoouline V., Esry B. D. 2003. Importance of Jahn–Teller coupling in the dissociative recombination of H3+ by low energy electrons. In Dissociative recombination of molecular ions with electrons (ed. Guberman S. L.), pp. 221–233 New York, NY: Kluwer/Plenum Publishers. [Google Scholar]
- 25.Jahn H. A., Teller E. 1937. Stability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy. Proc. R. Soc. Lond. A 161, 220–235 10.1098/rspa.1937.0142 (doi:10.1098/rspa.1937.0142) [DOI] [Google Scholar]
- 26.Kokoouline V., Greene C. H., Esry B. D. 2001. Mechanism for the destruction of H3+ ions by electron impact. Nature 412, 891–894 10.1038/35091025 (doi:10.1038/35091025) [DOI] [PubMed] [Google Scholar]
- 27.Suzor-Weiner A., Schneider I. F. 2001. Mystery of an interstellar ion. Nature 412, 871–872 10.1038/35091186 (doi:10.1038/35091186) [DOI] [PubMed] [Google Scholar]
- 28.McCall B. J., Oka T. 2003. Enigma of H3+ in diffuse interstellar clouds. In Dissociative recombination of molecular ions with electrons (ed. Guberman S. L.), pp. 365–371 New York, NY: Kluwer/Plenum Publishers. [Google Scholar]
- 29.Oka T. 2003. Help!!! Theory for H3+ recombination badly needed. In Dissociative recombination of molecular ions with electrons (ed. Guberman S. L.), pp. 209–220 New York, NY: Kluwer/Plenum Publishers. [Google Scholar]
- 30.Oka T. 2006. Introductory remarks. Phil. Trans. R. Soc. A 364, 2847–2853 10.1098/rsta.2006.1870 (doi:10.1098/rsta.2006.1870) [DOI] [PubMed] [Google Scholar]
- 31.McCall B. J., et al. 2003. An enhanced cosmic-ray flux towards ζ Persei inferred from a laboratory study of the H3+–e− recombination rate. Nature 422, 500–502 10.1038/nature01498 (doi:10.1038/nature01498) [DOI] [PubMed] [Google Scholar]
- 32.McCall B. J., Huneycutt A. J., Saykally R. J. 2004. Dissociative recombination of rotationally cold H3+. Phys. Rev. A 70, 052716. 10.1103/PhysRevA.70.052716 (doi:10.1103/PhysRevA.70.052716) [DOI] [Google Scholar]
- 33.McCall B. J., et al. 2005. Storage ring measurements of the dissociative recombination of rotationally cold H3+. J. Phys. Conf. Ser. 4, 92–97 10.1088/1742-6596/4/1/012 (doi:10.1088/1742-6596/4/1/012) [DOI] [Google Scholar]
- 34.Lammich L., et al. 2003. Evidence for subthermal rotational populations in stored molecular ions through state-dependent dissociative recombination. Phys. Rev. Lett. 91, 143201. 10.1103/PhysRevLett.91.143201 (doi:10.1103/PhysRevLett.91.143201) [DOI] [PubMed] [Google Scholar]
- 35.Kreckel H., et al. 2005. High resolution dissociative recombination of cold H3+ and first evidence for nuclear spin effects. Phys. Rev. Lett. 95, 263201. 10.1103/PhysRevLett.95.263201 (doi:10.1103/PhysRevLett.95.263201) [DOI] [PubMed] [Google Scholar]
- 36.Larsson M., Orel A. E. 2008. Dissociative recombination of molecular ions. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 37.Kreckel H., et al. 2010. High-resolution storage-ring measurements of the dissociative recombination of H3+ using a supersonic expansion ion source. Phys. Rev. A 82, 042715. 10.1103/PhysRevA.82.042715 (doi:10.1103/PhysRevA.82.042715) [DOI] [Google Scholar]
- 38.Kokoouline V., Greene C. H. 2003. Theory of dissociative recombination of D3h triatomic ions applied to H3+. Phys. Rev. Lett. 90, 133201. 10.1103/PhysRevLett.90.133201 (doi:10.1103/PhysRevLett.90.133201) [DOI] [PubMed] [Google Scholar]
- 39.Kokoouline V., Greene C. H. 2003. Unified theoretical treatment of dissociative recombination of D3h triatomic ions: applications to H3+ and D3+. Phys. Rev. A 68, 012703. 10.1103/PhysRevA.68.012703 (doi:10.1103/PhysRevA.68.012703) [DOI] [Google Scholar]
- 40.Jungen Ch., Pratt S. T. 2009. Jahn–Teller interactions in the dissociative recombination of H3+. Phys. Rev. Lett. 102, 023201. 10.1103/PhysRevLett.102.023201 (doi:10.1103/PhysRevLett.102.023201) [DOI] [PubMed] [Google Scholar]
- 41.Fonseca dos Santos S., Kokoouline V., Green C. H. 2007. Dissociative recombination of H3+ in the ground and vibrationally excited states. J. Chem. Phys. 127, 124309. 10.1063/1.2784275 (doi:10.1063/1.2784275) [DOI] [PubMed] [Google Scholar]
- 42.Glosik J., Plasil R., Poerya V., Kudrna P., Tichy M., Pysanenko A. 2001. Experimental study of recombination of H3+ ions with electrons relevant for interstellar and planetary plasmas. J. Phys. B 34, L485–L494 10.1088/0953-4075/34/15/104 (doi:10.1088/0953-4075/34/15/104) [DOI] [Google Scholar]
- 43.Plasil R., Glosik J., Poterya V., Kudrna P., Rusz J., Tichy M., Pysanenko A. 2002. Advanced stationary afterglow method for the experimental study of recombination of processes of H3+ and D3+ ions with electrons. Int. J. Mass Spectrom. 218, 105–130 10.1016/S1387-3806(02)00714-5 (doi:10.1016/S1387-3806(02)00714-5) [DOI] [Google Scholar]
- 44.Poterya V., Glosik J., Plasil R., Tichy M., Kudrna P., Pysanenko A. 2002. Recombination of D3+ ions in the afterglow of a He–Ar–D2 plasma. Phys. Rev. Lett. 88, 044802. 10.1103/PhysRevLett.88.044802 (doi:10.1103/PhysRevLett.88.044802) [DOI] [PubMed] [Google Scholar]
- 45.Glosik J., Novotny O., Pysanenko A. 2003. The recombination of H3+ and H5+ ions with electrons in hydrogen plasma: dependence on temperature and on pressure of H2. Plasma Sources Sci. Technol. 12, S117–S122 10.1088/0963-0252/12/4/027 (doi:10.1088/0963-0252/12/4/027) [DOI] [Google Scholar]
- 46.Novotny O., Plasil R., Pysanenko A., Korolov I., Glosik J. 2006. The recombination of D3+ and D5+ with electrons in deuterium containing plasma. J. Phys. B 39, 2561–2569 10.1088/0953-4075/39/11/019 (doi:10.1088/0953-4075/39/11/019) [DOI] [Google Scholar]
- 47.Macko P., Bano G., Hlavenka P., Plasil R., Poterya V., Pysanenko A., Votava O., Johnsen R., Glosik J. 2004. Afterglow studies of H3+ (v = 0) recombination using time resolved cw-diode laser cavity ring-down spectroscopy. Int. J. Mass Spectrom. 233, 299–304 10.1016/j.ijms.2003.12.035 (doi:10.1016/j.ijms.2003.12.035) [DOI] [Google Scholar]
- 48.Macko P., Bano G., Hlavenka P., Plasil R., Poterya V., Pysanenko A., Dryahina K., Glosik J. 2004. Decay of H3+ dominated low-temperature plasma. Acta Phys. Slov. 54, 263–271 [Google Scholar]
- 49.Plasil R., Hlavenka P., Macko P., Bánó G., Pysanenko A., Glosík J. 2005. The recombination of spectroscopically identified H3+ (v = 0) ions with electrons. J. Phys. Conf. Ser. 4, 118–125 10.1088/1742-6596/4/1/016 (doi:10.1088/1742-6596/4/1/016) [DOI] [Google Scholar]
- 50.Johnsen R. 2005. A critical review of H3+ recombination studies. J. Phys. Conf. Ser. 4, 83–91 10.1088/1742-6596/4/1/011 (doi:10.1088/1742-6596/4/1/011) [DOI] [Google Scholar]
- 51.Glosik J., et al. 2008. Recombination of H3+ ions in the afterglow of a He–Ar–H2 plasma. J. Phys. B 41, 191001. 10.1088/0953-4075/41/19/191001 (doi:10.1088/0953-4075/41/19/191001) [DOI] [Google Scholar]
- 52.Glosik J., Plasil R., Korolov I., Novotny O., Kotrik T. 2009. Multicollisional character of recombination of H3+ ions in afterglow plasma. J. Phys. Conf. Ser. 192, 012005. 10.1088/1742-6596/192/1/012005 (doi:10.1088/1742-6596/192/1/012005) [DOI] [Google Scholar]
- 53.Glosik J., et al. 2009. Binary and ternary recombination of D3+ ions with electrons in He-D2 plasma. Phys. Rev. A 80, 042706. 10.1103/PhysRevA.80.042706 (doi:10.1103/PhysRevA.80.042706) [DOI] [Google Scholar]
- 54.Glosik J., et al. 2009. Temperature dependence of binary and ternary recombination of H3+ ions with electrons. Phys. Rev. A 79, 052707. 10.1103/PhysRevA.79.052707 (doi:10.1103/PhysRevA.79.052707) [DOI] [PubMed] [Google Scholar]
- 55.Glosik J., et al. 2010. Binary and ternary recombination of H3+ and D3+ ions with electrons in low temperature plasma. Mol. Phys. 108, 2253–2264 10.1080/00268976.2010.507555 (doi:10.1080/00268976.2010.507555) [DOI] [Google Scholar]
- 56.Totrik T., Dohnal P., Korolov I., Plasil R., Roucka S., Glosik J., Greene C. H., Kokoouline V. 2010. Temperature dependence of binary and ternary recombination of D3+ ions. J. Chem. Phys. 133, 034305. 10.1063/1.3457940 (doi:10.1063/1.3457940) [DOI] [PubMed] [Google Scholar]
- 57.Johnsen R. 2011. Discrepancies between H3+ recombination rate coefficients measured in ion storage rings, afterglows, and theory. Are they ‘real’ or ‘apparent’?. J. Phys. Conf. Ser. 300, 012024. 10.1088/1742-6596/300/1/012024 (doi:10.1088/1742-6596/300/1/012024) [DOI] [Google Scholar]
- 58.Johnsen R., Guberman S. L. 2010. Dissociative recombination of H3+ ions with electrons: theory and experiment. Adv. At. Mol. Opt. Phys. 59, 75–128 10.1016/S1049-250X(10)59003-7 (doi:10.1016/S1049-250X(10)59003-7) [DOI] [Google Scholar]
- 59.Kokoouline V., Greene C. H. 2005. Theoretical study of C2v triatomic ions: application to H2D+ and D2H+. Phys. Rev. A 72, 022712. 10.1103/PhysRevA.72.022712 (doi:10.1103/PhysRevA.72.022712) [DOI] [Google Scholar]
- 60.Greene C. H., Kokoouline V. 2006. Theoretical progress and challenges in H3+ dissociative recombination. Phil. Trans. R. Soc. A 364, 2965–2980 10.1098/rsta.2006.1869 (doi:10.1098/rsta.2006.1869) [DOI] [PubMed] [Google Scholar]
- 61.Le Padellec A., Larsson M., Danared H., Larson A., Peterson J. R., Rosen S., Stromholm C. 1998. A storage ring study of dissociative excitation and recombination of D3+. Phys. Scr. 57, 215–221 10.1088/0031-8949/57/2/010 (doi:10.1088/0031-8949/57/2/010) [DOI] [Google Scholar]
- 62.Larsson M., et al. 1996. Dissociative recombination of H2D+ and the cosmic abundance of deuterium. Astron. Astrophys. 309, L1–L4 [Google Scholar]
- 63.Zhaunerchyk V., Thomas R. D., Geppert W. D., Hamberg M., Kaminska M., Vigren E., Larsson M. 2008. Dissociative recombination of D2H+: comparison between recent storage-ring results and theoretical calculations. Phys. Rev. A 77, 034701. 10.1103/PhysRevA.77.034701 (doi:10.1103/PhysRevA.77.034701) [DOI] [Google Scholar]
- 64.Pagani L., et al. 2009. Chemical modeling of L183 (L143N): an estimate of the ortho/para H2 ratio. Astron. Astrophys. 494, 623–636 10.1051/0004-6361:200810587 (doi:10.1051/0004-6361:200810587) [DOI] [Google Scholar]
- 65.Petrignani A., et al. 2007. Spectroscopy and dissociative recombination of the lowest rotational states of H3+. J. Phys. Conf. Ser. 192, 012022. 10.1088/1742-6596/192/1/012022 (doi:10.1088/1742-6596/192/1/012022) [DOI] [Google Scholar]
- 66.Tom B. A., et al. 2009. Dissociative recombination of highly enriched para-H3+. J. Chem. Phys. 130, 031101. 10.1063/1.3065970 (doi:10.1063/1.3065970) [DOI] [PubMed] [Google Scholar]
- 67.Crabtree K. N., Indriolo N., Kreckel H., Tom B. A., McCall B. J. 2011. On the ortho:para ratio of H3+ in diffuse clouds. Astrophys. J. 729, 15. 10.1088/0004-637X/729/1/15 (doi:10.1088/0004-637X/729/1/15) [DOI] [Google Scholar]
- 68.Varju J., Hejduk M., Dohnal P., Jilek M., Kotrik T., Plasil R., Gerlich D., Glosik J. 2011. Nuclear spin effects on recombination of H3+ ions with electrons at 77 K. Phys. Rev. Lett. 106, 203201. 10.1103/PhysRevLett.106.203201 (doi:10.1103/PhysRevLett.106.203201) [DOI] [PubMed] [Google Scholar]
- 69.Plasil R., Varju J., Hejduk M., Dohnal P., Kodrik T., Glosik J. 2011. Experimental study of para- and ortho-H3+ recombination. J. Phys. Conf. Ser. 300, 012023. 10.1088/1742-6596/300/1/012023 (doi:10.1088/1742-6596/300/1/012023) [DOI] [PubMed] [Google Scholar]
- 70.Larsson M., McCall B. J., Orel A. E. 2008. The dissociative recombination of H3+: a saga coming to an end?. Chem. Phys. Lett. 462, 145–151 10.1016/j.cplett.2008.06.069 (doi:10.1016/j.cplett.2008.06.069) [DOI] [Google Scholar]
- 71.Petrignani A., et al. 2011. Resonant structure of low-energy H3+dissociative recombination. Phys. Rev. A 83, 032711. 10.1103/PhysRevA.83.032711 (doi:10.1103/PhysRevA.83.032711) [DOI] [Google Scholar]