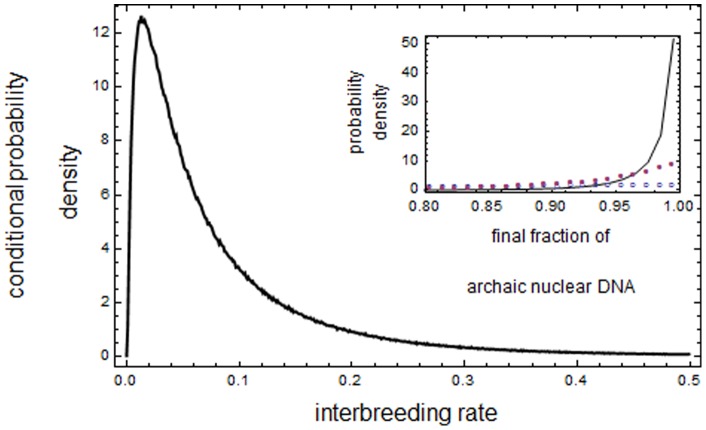
Figure 3. The probability density for 
.
We show here the probability density that the final value of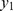 
is in the experimental interval 0.96–0.99 as a function of 
. The plot was built by obtaining one million “successful” pairs 
such that subpopulation 2 is extinct and the final value of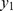 
– obtained by solving (1) – lies in the experimental interval. These pairs were obtained out of a total of around 140 million simulated Wright-Fisher paths 
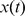with random 
uniformly distributed between 0 and 0.8 and 
uniformly distributed between 0 and 2. For the successful pairs we then computed the fraction associated to any given 
. In the inset we plot the probability density for the final values of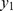 
for three different values of 
. The densities are empirically determined by simulating 400,000 Wright-Fisher paths 
with random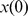 
uniformly distributed between 0 and 1 and selecting the histories in which subpopulation 2 is extinct. The empty dots (blue) are data for 
, the full dots (purple) are data for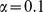 
and the full curve (black) are for 
.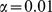