Seeing is Believing: Video Classification for Computed Tomographic Colonography Using Multiple-Instance Learning

Abstract

In this paper we present development and testing results for a novel colonic polyp classification method for use as part of a computed tomographic colonography (CTC) computer-aided detection (CAD) system. Inspired by the interpretative methodology of radiologists using 3D fly-through mode in CTC reading, we have developed an algorithm which utilizes sequences of images (referred to here as videos) for classification of CAD marks. For each CAD mark, we created a video composed of a series of intraluminal, volume-rendered images visualizing the detection from multiple viewpoints. We then framed the video classification question as a multiple-instance learning (MIL) problem. Since a positive (negative) bag may contain negative (positive) instances, which in our case depends on the viewing angles and camera distance to the target, we developed a novel MIL paradigm to accommodate this class of problems. We solved the new MIL problem by maximizing a L2-norm soft margin using semidefinite programming, which can optimize relevant parameters automatically. We tested our method by analyzing a CTC data set obtained from 50 patients from three medical centers. Our proposed method showed significantly better performance compared with several traditional MIL methods.

I. Introduction

Colon cancer is the second leading cause of cancer-related death in the United States [1]. Computed tomographic colonography (CTC), also known as virtual colonoscopy when a fly-through viewing mode is used, provides a less invasive alternative to optical colonoscopy in screening patients for colonic polyps. Computer-aided polyp detection software has improved rapidly and is accurate [2–16].

In clinical practice, when a suspicious lesion (polyp candidate) is found on CTC, a radiologist will observe it from different viewing angles and distances with the help of the CTC visualization software before making a final diagnostic assessment. Different viewing angles and varying distances reveal various diagnostic characteristics of the polyp candidate, and each may incrementally increase diagnostic confidence. We hypothesized that combining these viewpoints into a visualization set for CAD classification could lead to higher sensitivity and a lower false positive rate. By analyzing and modeling the interpretative methodology of radiologists, we have developed a novel algorithm for the classification of colonic polyp candidates identified by a CAD system. For each polyp candidate, our system creates a short video, illustrating the detection from various viewpoints. We created a computer vision algorithm to analyze the captured multi-perspective polyp candidate videos to classify these suspicious candidate locations following a similar observational approach to that of an experienced radiologist. Given a training set of captured polyp candidate videos and corresponding ground truth labels, the problem becomes one of how the computer can learn from the training videos and make accurate predictions for a set of test cases.

In this paper, we illustrate a solution to the video classification problem using multiple-instance learning (MIL). MIL is currently a topic of great interest in the field of machine learning [17–28]. As a variant of supervised learning, where individual instances are labeled as positive or negative, MIL wraps instances (or samples) in “bags.” A bag is defined as an ensemble of instances. The learner (computer learning algorithm) knows the labels of bags, but cannot identify the labels of the individual instances within each bag. A bag is labeled negative if all the instances in it are negative, and is labeled positive if it contains at least one positive instance. Given training bags of instances and corresponding bag labels, MIL methods can train a computerized learner to predict the labels of unknown test bags.

Multi-instance learning was first formulated by Dietterich et al. in the study of drug activity prediction [17]. Dietterich’s approach seeks to define an axis-parallel hyper-rectangle (APR) that would enclose at least one instance from each positive bag and exclude all instances from negative bags. Maron and Lozano-Pérez proposed an alternative framework for MIL, diverse density [19]. This algorithm searches for a concept point in feature space that is both close to instances from many different positive bags and distant from instances in negative bags. This approach was extended by introducing an expectation maximization algorithm for estimating which instance(s) in a bag is responsible for the assigned class label [20]. Wang and Zucker described a lazy MIL framework based on the classic k-nearest neighbor (k-NN) classifier [21]. Their proposed method, citation-kNN, uses the Hausdorff distance to measure the distance between bags and considers both ‘citers’ and ‘references’ to calculate neighbors. Later, kernel methods for MIL were developed [22–24]. Andrews et al. extended the support vector machine (SVM) learning approach to MIL [22]. In their MISVM formulation, they generalize the SVM notion of margin maximization to bags, training the classifier using only the most positive instances from positive bags and the least negative instances from negative bags. In their miSVM formulation, they treat instance labels as unobserved integer variables constrained by the bag labels. This algorithm maximizes the soft-margin jointly over the hidden label variables and a linear discriminant function. MIL has also found application in medical CAD problems. Fung et al. developed a Convex Hull based Fisher’s Discriminant MIL algorithm (CH-FD) to learn a convex hull representation of multiple instances, and they applied their technique to the detection of pulmonary embolism in computed tomography angiography and colonic polyps in CTC [25]. They relaxed the MIL problem via convex hulls and solved it based on Fisher’s linear discriminant criterion. Ensemble methods have also been developed for MIL [26–28].

A video is composed of a series of frames or images. In our case, each detection’s video is treated as a bag, and each frame of the video is treated as a separate instance. A MIL model is then constructed to solve the video classification problem. Bag labels are defined based on histopathological findings, and the final evaluation is done on the bag level. Instances are defined qualitatively. Positive instances are those frames that have visual features that strongly resemble a true polyp. Negative instances do not visually resemble a true polyp. We collect the frames from a video illustrating a true polyp into a positive bag and frames from a video of a false positive detection into a negative bag. As each video only focuses on a single point on the colonic surface, positive bags would ideally contain purely positive instances. Similarly, negative bags should contain exclusively negative instances. However, we observed that the visual information in the videos can belie these assumptions. It is true that the video of a false positive detection will normally not contain a positive instance (unless there is a different true polyp in the very close vicinity). However, due to the complex nature of the colon surface, various viewing angles and camera distances used in making the video may cause ambiguous visual information. The ambiguous visual information in our application is highlighted in Fig. 1 which demonstrates how frames that focus on true positive/false negative detections can be described as negative/positive instances. Thus, traditional MIL methods, which rigidly assume that all instances in a negative bag are negative samples, do not fit the constraints of our problem very well. Relaxing this assumption and allowing positive instances in a negative bag may provide a benefit in the classification problem. In this study, we developed a novel MIL learning technique which allows both positive and negative instances to exist in either a positive or negative bag.

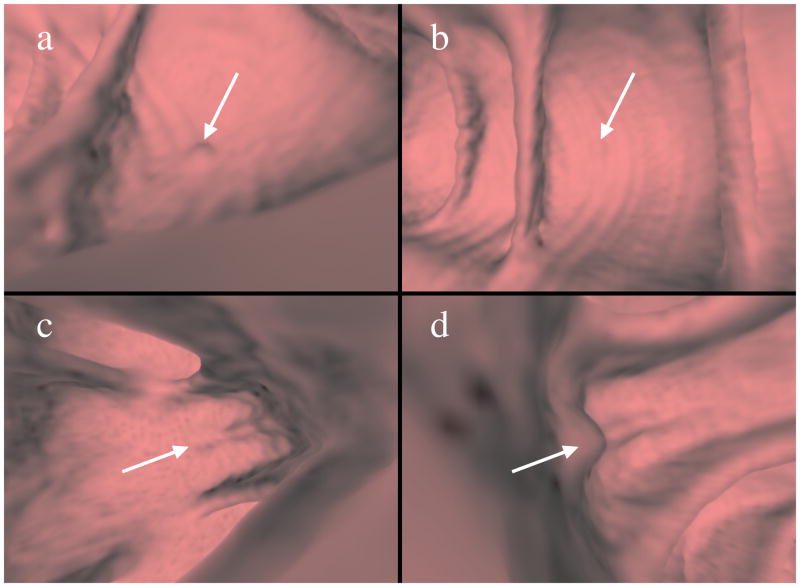
Fig. 1.

Need for instance ranking. Images (a) and (b) are taken from a positive bag that illustrates a 6 mm sessile polyp, while images (c) and (d) are from a negative bag showing a false positive at the base of a fold. Images (a) and (c) show instances of the detections that should be preferred as they are more representative of their respective classes. Instances in (b) and (d) appear misleading and could lead to incorrect classification.

The outline of the paper is as follows: in Section II we clarify our motivation for this method; in Section III we introduce our video capture model and feature extraction module; in Section IV, the new MIL method is proposed; in Section V we describe our dataset and evaluation method; in Section VI, results of the novel MIL analysis are detailed, with conclusions provided in Section VII.

II. Motivation

Our aim is to further improve CTC CAD systems to make them more valuable to physicians in diagnosing patients. We want to identify those detections with high probabilities of being true polyps. Further, we would like to identify viewpoints of those marks that may be particularly revealing. We were inspired by the interpretative methodology of radiologists, and we believe that a system that mimics their approach could prove beneficial. In psychological research on object understanding, theories generally fall into one of two classes: those that rely on 3D, object-centered representations or those that rely on 2D, view-centered representations. Experiments have found viewpoint-dependent performance in object recognition tasks. This suggests that object recognition by humans may be better described by a 2D, image-matching approach than a method relying on 3D models [29, 30]. While there is support for a 3D approach, which in theory would provide viewpoint-invariant performance, these theories are subject to constraints – notably that the object must decompose into the same set of 3D sub-structures regardless of viewpoint [31]. These conditions may not be met in reading TMI-2011-0874 3 CTC studies, and a 2D model may be more representative of the interpretative process. Thus, our method tries to mimic the reading behavior of radiologists, who could experience 3D images as a series of projected 2D images. We received further motivation for this approach from results of a recent observer performance study where naïve observers using only 2D information achieved a performance level not significantly different from that of a CAD system relying on 3D analysis [4]. Two-dimensional projection features also have been used to improve the sensitivity of CAD systems for CTC [6]. We argue that analysis of 2D images by our improved MIL method yields valid and useful information that is not immediately available in a direct analysis of 3D images. For example, we can utilize structures in the colon that appear nearby in the 2D images to assist in classification. A framework for using this auxiliary information for 3D analysis is usually ignored due to computational issues. While applying image analysis directly to 3D images is an important concept that has been a popular focus of research, this paper approaches the classification problem in CTC from the viewpoint of computer vision.

The MIL framework is uniquely structured to handle our problem. Traditional approaches for video classification often focus on the temporal relationship between frames, and the features and classifiers used to describe these videos usually reflect that temporal dependence [32]. Our approach is viewpoint-based and our generated frames do not have strong temporal correlations, so such temporally-dependent methods, such as hidden Markov models, which are widely used for video classification, do not fit our problem. We handle a video as a radiologist may, treating each frame as a separate but closely related description of a detection. We observe that the visual information content from each frame may be ambiguous; however, when a video is considered as a set, we hypothesize the combined information from various viewpoints could lead to a strong classifier. The MIL framework allows for such an approach. MIL can explicitly treat videos as groups, using each viewpoint to incrementally improve diagnostic performance. This framework allows us to incorporate additional information relative to traditional 3D CTC CAD, which only analyzes voxels in the immediate vicinity of a detection. Our MIL approach can effectively consider global, contextual information that could influence diagnosis.

III. Video capture and feature extraction for colonic polyp candidates in ctc

A. Image Generation

Volumetric ray-casting with perspective projection was used with a segmented, but uncleansed CTC dataset, to generate the images [33]. A two dimensional opacity transfer function was created for each polyp candidate (PC), which varied with CT intensity values and gradient measures. Fluid subtraction was performed by a suitable selection of transfer functions. Such an approach seeks to avoid the creation of polyp-like structures arising from poor segmentation. A color transfer function was set in conjunction with the opacity transfer function to better illustrate the three materials most often present: air (blue), tissue (red), and contrast (green). The rendering pipeline was implemented with VTK [34], and the rendering functions were inspired by those in [6].

B. Viewpoint Selection

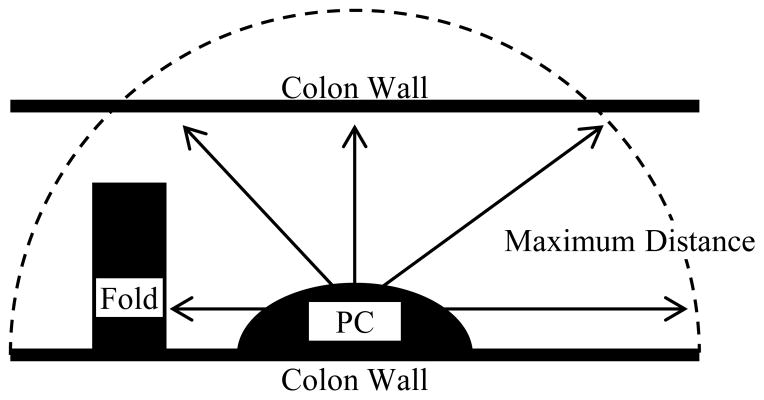
We used colonic segmentation results to generate multiple valid viewpoints for each PC. To generate the viewpoints, we first aligned a sampled hemisphere (81 points) with the measured surface normal of the PC. We sampled the hemisphere at specified spherical coordinate intervals (every π/8 radians azimuth and every π/10 radians inclination). Using each point in the hemisphere to define a direction, a camera was iteratively moved away from the PC centroid in each direction. The camera movement was stopped when it either hit tissue or exceeded a maximum distance from the centroid. Generating viewpoints in this way ensured the visibility of the centroid, and larger distances allowed us to capture contextual information of diagnostic importance. Fig. 2 illustrates the viewpoint generation process.

Fig. 2.

Illustration of viewpoint generation process. Cameras (represented by arrows) are moved from the PC centroid in various directions until they hit tissue (e.g. colon wall or fold) or reach a maximum distance from the PC centroid.

To limit the dimensionality of our classification problem, we used an iterative ranking scheme to select viewpoints. We initially used three criteria to rank the viewpoints: alignment with the principal components of the PC, alignment with the fluid normal, and distance from the PC centroid. As the ranked list became populated we penalized subsequent viewpoints for sharing a similar alignment with a previously-selected viewpoint. In our observations, these criteria produced a range of informative viewpoints.

The three principal components of the polyp candidate were extracted from the 3D arrangement of the voxels marked as part of the detection using principal component analysis. Assuming viewpoints on the same side as the polyp candidate normal are more informative, the principal component vectors were aligned with the normal such that the scalar product of each vector with the normal was positive. We also assumed viewpoints situated at 45 degrees with respect to each principal component would be informative. Such viewpoints were chosen to capture the shape of the detection.

A distance score which increased with distance from the detection centroid was assigned to ensure the polyp candidate was not distorted in creating the image. Since we used perspective projection to generate the images, a viewpoint very close to the polyp candidate could distort the candidate. Farther viewpoints also allow for capture of structures of possible diagnostic significance surrounding the detection.

Alignment with the fluid normal was considered to account for the presence of contrast in the images. Volume averaging effects at air-fluid interfaces resulted in a thin film with intensities comparable to tissue. While the gradient component of the transfer function was designed to render the film transparent, a viewpoint that runs parallel to such a surface would produce an occluded image of the polyp candidate. Rendering performance improves as the viewpoint is increasingly orthogonal to the fluid’s surface. Viewpoints that penetrate this air-fluid interface were assigned scores based on their alignment with the surface normal of the fluid.

To ensure different viewpoints were selected, a given viewpoint was penalized for having a similar alignment with previously selected viewpoints.

The viewing angle of the camera was set to ensure the entire PC would be visible. The PC’s voxels were first projected onto the plane running through the PC centroid and orthogonal to the viewing direction. The major principal component of the projection and the distance from the centroid to the farthest voxel in that direction, R, were measured. The camera was then aligned with this vector, and the viewing angle set using the geometric relationship between the camera’s distance from the detection centroid and R. Multiple scales were investigated by adding a multiplier, m, to the R measure and recalculating the angle. We generated 400×400 pixel images at three scales (m = 1, 2, 3) for each viewpoint (3 images per viewpoint). We conducted experiments to determine the optimal number of viewpoints (instances) per detection (bag). In Fig. 3 we show some frames depicting the viewing angles and scales used.

Fig. 3.

Representative frames extracted from typical videos with different viewpoints and viewing angles. Images (a)–(d) show true polyps. Image (a) shows a 6 mm sessile polyp, (b) a 1.1 cm sessile polyp, (c) a 1.1 cm pedunculated polyp, and (d) a 6 mm sessile polyp. Images (e)–(h) show common false positives. Image (e) shows a detection on a haustral fold, (f) an air bubble false positive, (g) a detection arising from rough texture, and (h) a detection on a taenia coli. The green color in (b), (f), and (g) demonstrates that the detection is covered in iodinated endoluminal contrast material.

C. Feature Extraction

We implemented a set of low-level, statistical features to analyze each frame of our videos. The selected features do not require a segmentation result making them particularly applicable to our approach. Segmentation in these video sequences often proves difficult as the object of interest often blends in with the surrounding structures. Features based on a requisite segmentation also would lessen the utility of the approach, as local, segmentation-based features exclude the detection’s relation to surrounding structure.

We included a subset of features from the MPEG-7 standard: color structure, scalable color, dominant color, color layout, homogeneous texture, and edge histogram. The MPEG-7 standard, formally named Multimedia Content Description Interface, defines standard methods to describe multimedia content to allow for searching of audio and visual content [35, 36]. These features have been successfully employed in several video-based endoscopic CAD systems. One such system uses MPEG-7 descriptors to detect events in capsule endoscopy in the small bowel [37]. Another uses the descriptors to diagnose Crohn’s disease in capsule endoscopy [38].

Inspired by other CAD systems designed to detect polyps in videos taken during traditional colonoscopy, we used the grayscale wavelet cooccurence and color wavelet covariance features (Wavelet) proposed in [39, 40]. As virtual colonoscopy mimics traditional colonoscopy, we believe that these features would perform well in our application. We also included the local binary pattern histogram Fourier features (LBP) proposed in [41]. This feature has been applied successfully to texture recognition problems.

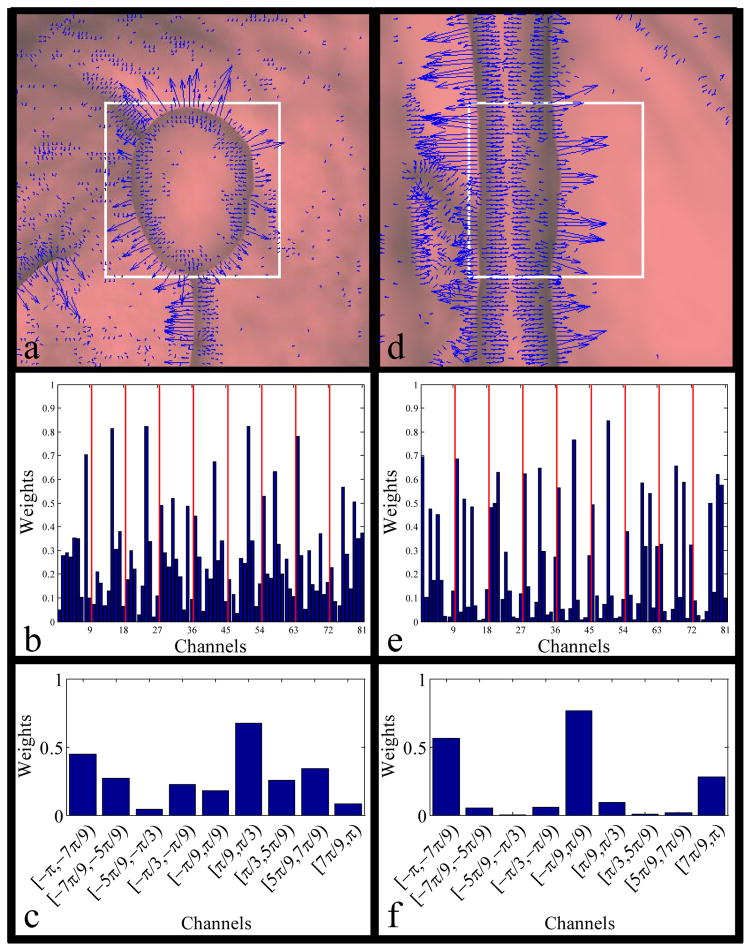
A histogram of oriented gradients (HOG), a feature set which has been proposed for use in visual object recognition in 2D static color images [42], was generated for each frame in the videos. This feature set provides a measure of the shapes and edges in the videos. In our implementation, we calculated the vertical and horizontal gradients of our image and used trigonometric relationships to define the gradient magnitude and direction at each pixel. We then covered that gradient image with 9 overlapping blocks (200×200 pixels; block overlap is fixed at half of the block size; block centers at (100,100), (200,100), (300,100), (100,200), (200,200), (300,200), (100,300), (200,300), and (300,300) in pixel coordinates (origin at top left of image)). For each block, we created a 9-channel histogram to capture both the gradient magnitudes and orientations. Each channel represented a range of angles in [−π, π), and we used the magnitude of the gradient at each point to weight that pixel’s contribution to the histogram. We normalized each block’s histogram and concatenated histograms from each block to generate the final feature vector. We selected these parameters based on suggestions in the original paper. See Fig. 4 for an illustration of the HOG feature.

Fig. 4.

Illustration of HOG. We show two sample detections with oriented gradients overlaid in blue. Image (a) shows an 1.5 cm pedunculated polyp, and (b) shows the corresponding HOG descriptor. (c) shows the HOG descriptor for the area denoted by the white box in (a). Image (d) shows a fold (false positive), and (e) shows its HOG descriptor. (f) shows the HOG descriptor the for the area denoted by the white box in (d). Note the round shape of the true polyp in (a) translates to a histogram whose response is more distributed than the HOG of (d), in which most of the gradients lie along the same direction.

We adapted the shape context feature (SC) proposed in [43] for our application. We used a Canny edge detector to extract the boundaries in each frame and translated the boundaries into polar coordinates (r, θ). r is the distance from the center of the image, and r ≥0. θ falls in (−π, π] and represents the counterclockwise angle from the vector running right from the center of the image. A single log-polar histogram was used to collect these points. We used the parameters suggested in the paper, with 5 bins for log r and 12 bins for θ. Similar to HOG, this feature provides a description of the shapes and edges in the videos.

We also included a set of features derived from the projections used to find the viewing angles (Projection). We used the shape context approach to collect the distribution of the projected voxels to further describe the detection’s shape. The principal components of the projected voxels and the distances from the centroid to the farthest voxel in each of those directions were recorded to indicate the orientation and size of the detection. Camera parameters, such as viewing angle and distance to centroid also were used as features.

We calculated these features for every frame generated. To account for our multiscale approach, we concatenated all features from frames taken from the same viewpoint at different scales into a single vector. This resulted in a feature vector for each viewpoint (instance) with 2367 descriptors as described in Table 1.

Table 1.

Description of feature vector

Feature	MPEG	Wavelet	LBP	HOG	SC	Projection
Length	1386	360	114	243	180	84

Although the particular choices we made in frame generation and feature extraction may affect the classification performance, it is expected that the effects would not be strongly algorithm-dependent, i.e., the ordering of algorithm performance is not expected to be different for other choices for frame generation and feature extraction. For example, we would expect our classification algorithm to achieve similar performance relative to other MIL methods if we had used a different transfer function to generate the image or a different set of features to describe each frame.

IV. A new multiple-instance learning paradigm using semidefinite programming for L2-norm soft margin maximization

In MIL, data are collected and presented in a two-level (bag level and instance level) hierarchal form. Each instance is associated with a bag and a bag contains one or more instances. We only have labels for bags and do not have labels for instances. More formally, let X ∈ ℝ^k be the input space of instances where k is the number of features and Y = {−1,+1} be the set of class labels. Given a set of training bags {(B₁,y₁),…, (B_m,y_m)}, where B_i is the ith bag containing instances x_j ∈ X, j = 1,2,…, n_i, where n_i is the number of instances in the ith bag, y_i ∈ Y is the ith bag’s label, and y=[y₁,…,y_m], the purpose of MIL is to find a discriminant function f : X → ℝ which fits the training set under certain criteria and generalizes well on new test bags. Note that the discriminant function f is applied to instances, and that the label of each bag can be inferred from the classification results of instances. Let the first m_p bags in the training set be positive and the rest m_n bags be negative (m_p + m_n = m). Let n_p be the number of instances in all positive bags and n_n be the number of instances in all negative bags, such that n = n_p + n_n is the total number of instances in the training set.

As mentioned previously, video captured from a false detection (negative bag) may contain frames which look like true polyps. These frames, representing data points very dissimilar from other instances in their respective bags, arise from a variety of etiologies including segmentation, contrast agent, viewing angle of the camera, and distance of the camera to the PC. The traditional MIL will not fit within the constraints of our problem, as a negative bag may also contain positive instances. Based on this assumption, the above settings, and using the idea of maximum margin from SVM, our MIL problem can be formulated (following [18]) as follows:

$$\begin{array}{l}\underset{\mathbf{\eta }}{min}\underset{\mathbf{w},b,\mathbf{\xi }}{min}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\sum _{i=1}^n\frac{{\xi }_i^2}{{\eta }_i}\\ s.t.y_i\left({\mathbf{w}}^T\phi ({\mathbf{x}}_i)+b\right)\ge 1-{\xi }_i,{\forall }_{i=1}^n,{\xi }_i\ge 0,\\ \mathbf{0}<\mathbf{\eta }\le \mathbf{1},\mathbf{A}\mathbf{\eta }\le T\mathbf{e},\end{array}$$ (1)

where w ∈ℝⁿ and b correspond to the weight and bias of the linear classifier to be learned; η = [η_p; η_n] is a weighting vector which ranks positive (negative) instances in a positive (negative) bag (η_p = [η₁, η₂,…, η_np] corresponds to n_p positive instances; η_n = [η₁, η₂,…, η_nn] corresponds to n_n negative instances); 0 and 1 are each vectors with all 0’s or 1’s respectively; C is a constant introduced to solve the imbalance problem in true instances and false instances; ξ = [ξ_p; ξ_n] contains relaxation variables for non linear separable problems in feature space (of instances) (ξ_p = [ξ₁, ξ₂,…, ξ_np] corresponds to n_p positive instances; ξ_n = [ξ₁, ξ₂,…, ξ_nn] corresponds to n_n negative instances); y_i = +1 if the corresponding instance belongs to a positive bag and y_i = −1 if the corresponding instance belongs to a negative bag; e = {1}ⁿ denotes a vector with all 1 entries; T is a scalar threshold to control the weighted instances in a bag; x₁,…,x_n are training instances from training bags; Φ = [φ (x₁),…, φ (x_n)] are mappings of original instances in a high dimensional space. Each training instance was a feature vector extracted from a frame of a video of polyp candidate. A is a m x n binary matrix, and A(i,j) = 1 if instance j belongs to bag i. It corresponds to instance selection in our CTC CAD problem. For inequalities involving vectors x ∈ ℝⁿ and y ∈ ℝⁿ, the comparison is done element-wise, e.g., x < y, if x_i < y_i for i=1,2,…,n.

In the above formulation of the MIL problem, we used the L2-norm instead of the L1-norm employed by [18]. The solution to the L1-norm MIL problem contains a bilinear term, making it non-convex. Although the authors of [18] modified the solution to remove the bilinear term, we found their solution led to an unbounded objective function in practice. In addition, a previous study showed that the L2-norm is better than the L1-norm in video classification when information from different sources are complementary [44]. In our problem, frames from different viewpoints show different polyp candidate characteristics which may complement each other in making a classification. In the following, we will show solutions of the L2-norm MIL problem and how the bilinear problem can be avoided naturally.

Proposition 1

By using the Lagrange multiplier optimization method, the above minimization problem (1) can be formulated as the following dual problem:

$$\begin{array}{l}\underset{\mathbf{\eta }}{min}\underset{\mathbf{\alpha }}{max}{\mathbf{\alpha }}^T\mathbf{e}-\frac{1}{2}{\mathbf{\alpha }}^T\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })\right)\mathbf{\alpha }\\ s.t.\mathbf{\alpha }\ge \mathbf{0},{\mathbf{\alpha }}^T\mathbf{y}=0,\mathbf{0}<\mathbf{\eta }\le \mathbf{1},\mathbf{A}\mathbf{\eta }\le T\mathbf{e},\end{array}$$ (2)

where ∘ is an inner product, y = [y₁,…,y_m], K ∈ ℝ^nxn is the kernel matrix constructed from all training instances which captures similarities between instances K(x_i, x_j)=〈φ (x_i), φ(x_j)〉, and α ∈ ℝⁿ is a dual variable (vector) introduced in the Lagragian multiplier optimization method which determines support vectors. diag is the notation for a diagonal matrix.

In the following paragraph, we will show how to solve the above min-max optimization problem using semidefinite programming (SDP).

Theorem 1

The min-max optimization problem in (2) is equivalent to the following semidefinite programming problem:

$$\begin{array}{l}\underset{\mathbf{\eta },\mathbf{\mu },\epsilon }{min}\delta s.t.\left(\begin{array}{cc}\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })& (\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})\\ {(\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})}^T& 2\delta \end{array}\right)\ge 0,\\ \mathbf{0}<\mathbf{\eta }\le \mathbf{1},\mathbf{A}\mathbf{\eta }\le T\mathbf{e},\mathbf{\mu }\ge \mathbf{0}.\end{array}$$ (3)

where μ ∈ ℝⁿ and ε ∈ ℝ are auxiliary variables introduced for the dual problem.

Proof

(Extended from [18] to our new MIL paradigm and L2-norm soft margin) Let L(α,η,μ,ε) be the Lagrangian of the maximization problem in (2):

$$L(\mathbf{\alpha },\mathbf{\eta },\mathbf{\mu },\epsilon )={\mathbf{\alpha }}^T\mathbf{e}-\frac{1}{2}{\mathbf{\alpha }}^T\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })\right)\mathbf{\alpha }+{\mathbf{\mu }}^T\mathbf{\alpha }+\epsilon {\mathbf{\alpha }}^T\mathbf{y}.$$ (4)

Since L(α,η,μ,ε) is concave in α, the optimal α can be identified by setting:

$$\frac{\partial L(\mathbf{\alpha },\mathbf{\eta },\mathbf{\mu },\epsilon )}{\partial \mathbf{\alpha }}=\frac{\partial }{\partial \mathbf{\alpha }}\left({\mathbf{\alpha }}^T\mathbf{e}-\frac{1}{2}{\mathbf{\alpha }}^T\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })\right)\mathbf{\alpha }+{\mathbf{\mu }}^T\mathbf{\alpha }+\epsilon {\mathbf{\alpha }}^T\mathbf{y}\right)=0\Rightarrow {\mathbf{\alpha }}_{max}={\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })\right)}^{-1}\times (\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y}).$$ (5)

Substituting (5) into Lagrangian (4), we will get

$$L(\mathbf{\alpha },\mathbf{\eta },\mathbf{\mu },\epsilon )=\frac{1}{2}{(\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})}^T{\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })\right)}^{-1}\times (\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y}).$$ (6)

After solving the inner maximization problem in (2), we can convert it into the following minimization optimization problem:

$$\begin{array}{l}\underset{\mathbf{\eta },\mathbf{\mu },\epsilon }{min}\delta s.t.\delta \ge \frac{1}{2}{(\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})}^T{\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })\right)}^{-1}(\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y}),\\ \mathbf{0}<\mathbf{\eta }\le \mathbf{1},\mathbf{A}\mathbf{\eta }\le T\mathbf{e}.\end{array}$$ (7)

By using the Schur complement lemma, we get the semidefinite programming problem shown in (3). (End of Proof)

Please note that the bilinear term seen in the L1-norm MIL solution in Theorem 1 of [18] is eliminated in (3). The term was avoided naturally by using the L2-norm.

Let us consider optimization of threshold T in MIL with imbalanced data between positive and negative bags. Here we impose different thresholds on the relaxation variables T for positive and negative bags. We also used different cost coefficient C for positive and negative bags.

$$\begin{array}{l}\underset{\mathbf{\eta },T_p,T_n}{min}\underset{\mathbf{w},b,\mathbf{\xi }}{min}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C_p\sum _{i=1}^{n_p}\frac{{\xi }_i^2}{{\eta }_i}+C_n\sum _{i=n_p+1}^n\frac{{\xi }_i^2}{{\eta }_i}\\ s.t.y_i\left({\mathbf{w}}^T\phi ({\mathbf{x}}_i)+b\right)\ge 1-{\xi }_i,{\forall }_{i=1}^n,{\xi }_i\ge 0,\\ \mathbf{0}<\mathbf{\eta }\le \mathbf{1},{\mathbf{A}}_p{\mathbf{\eta }}_p\le T_p\mathbf{e},{\mathbf{A}}_n{\mathbf{\eta }}_n\le T_n\mathbf{e},T_p\le 1,T_n\le 1,\end{array}$$ (8)

where C_p and C_n are scalar constants introduced to solve imbalance problem in true instances and false instances; T_p and T_n are scalar variables to be optimized which control the selection of instances from bags. A_p is the first m_p rows of A, and A_n is the last m_n rows of A. C_p and C_n will impose different weights on slack variables of positive and negative bags, respectively. It is a typical strategy to deal with unbalanced datasets in large margin based learning methods [45]. T_p and T_n were introduced to select most representative instances from positive and negative bags, respectively.

By fixing η and maximizing the inner optimization problem over α, we can convert the above problem to the following SDP problem in Theorem 2.

Theorem 2

The MIL problem for unbalanced data and different bag thresholds shown in (8) is equivalent to the following SDP problem (please see Appendix A for proof):

$$\begin{array}{l}\underset{\mathbf{\eta },\mathbf{\mu },\epsilon }{min}\delta s.t.\left(\begin{array}{cc}\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C_p}\left(\begin{array}{cc}\mathit{diag}({\mathbf{\eta }}_p)& 0\\ 0& 0\end{array}\right)+\frac{1}{C_n}\left(\begin{array}{cc}0& 0\\ 0& \mathit{diag}({\mathbf{\eta }}_n)\end{array}\right)& (\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})\\ {(\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})}^T& 2\delta \end{array}\right)\ge 0,\\ \mathbf{0}<\mathbf{\eta }\le \mathbf{1},{\mathbf{A}}_p{\mathbf{\eta }}_p\le T_p\mathbf{e},{\mathbf{A}}_n{\mathbf{\eta }}_n\le T_n\mathbf{e},T_p\le 1,T_n\le 1,\end{array}$$ (9)

Based on the Lagrangian shown in (14) the Karush-Kuhn-Tucker (KKT) conditions for optimal w and b are:

$$\begin{array}{l}\frac{\partial L(\mathbf{w},b,\mathbf{\xi },\mathbf{\alpha })}{\partial \mathbf{w}}=\mathbf{w}-\sum _{i=1}^n{\alpha }_i{y}_i\phi ({\mathbf{x}}_i)=0\\ \Rightarrow \mathbf{w}=\sum _{i=1}^n{\alpha }_i{y}_i\phi ({\mathbf{x}}_i)\\ \frac{\partial L(\mathbf{w},b,\mathbf{\xi },\mathbf{\alpha })}{\partial b}=\sum _{i=1}^n{\alpha }_i{y}_i=0.\end{array}$$ (10)

b can be solved using any support vector i:

$$y_i\left({\mathbf{w}}^T\phi ({\mathbf{x}}_i)+b\right)=1\Rightarrow b=y_i-{\mathbf{w}}^T\phi ({\mathbf{x}}_i)=y_i-\sum _{j=1}^n{\alpha }_j{y}_j\mathbf{K}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right).$$ (11)

In practice, we averaged b calculated from all support vectors to get a stable solution.

For a test bag, we feed each test instance (x_t) inside it to the learned classifier to get predicted label (y_t):

$$\begin{array}{l}{y}_t={\mathbf{w}}^T\phi ({\mathbf{x}}_t)+b=\sum _{i=1}^n{\alpha }_i{y}_i\phi ({\mathbf{x}}_i)\times {\phi }^T({\mathbf{x}}_t)+b\\ =\sum _{i=1}^n{\alpha }_i{y}_i\mathbf{K}({\mathbf{x}}_i,{\mathbf{x}}_t)+b,\end{array}$$ (12)

where

$$\mathbf{\alpha }={\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C_p}\left(\begin{array}{cc}\mathit{diag}({\mathbf{\eta }}_p)& 0\\ 0& 0\end{array}\right)+\frac{1}{C_n}\left(\begin{array}{cc}0& 0\\ 0& \mathit{diag}({\mathbf{\eta }}_n)\end{array}\right)\right)}^{-1}\times (\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y}).$$ (13)

With the predictions of all the instances of the test bag, there are different strategies we can employ to estimate the bag label or prediction. We can rank all the instances first based on their predictions, then determine the bag prediction using the maximum (which was adopted by MISVM), minimum, or median instance prediction. Alternatively the prediction of the test bag can be determined using the average of all predictions of instances inside the test bag. In practice, we found that using the averaged instance predictions as the bag prediction achieved the best performance.

V. Data Set and Evaluation Method

Our evaluation data set consists of CTC examinations from 50 patients collected from three medical centers from a database of patients originally accrued during the study described by Pickhardt et al. [46]. Each patient was scanned in the supine and prone positions. Each scan was performed with a single breathhold CT protocol, using a 4-channel or 8-channel CT scanner. CT scanning parameters included 1.25- to 2.5-mm section collimation, 15 mm/s table speed, 1-mm reconstruction interval, 100 mAs, and 120 kVp. Each patient had one or more polyps ≥6mm confirmed by histopathological evaluation following optical colonoscopy. This data set was analyzed with a pre-existing CAD system to generate the initial list of polyp candidates, resulting in 91 true-positive locations of 53 polyps and 5233 false positive detections [5]. This system automatically segments the colon and identifies polyp candidates using features based on colonic surface curvature. We created a video for each of these detections, and we extracted 2367 features from each viewpoint as described in Table 1. We performed feature selection and varied the number of instances used to represent each CAD mark to see how those parameters impact performance.

To demonstrate the effectiveness of our proposed MIL method, we compared it with several MIL methods implemented with MILL [47]: diverse density (DD), axis-parallel rectangle (APR), citation-kNN (CKNN), mi-SVM, and MI-SVM. For DD, 10 random runs were conducted and results were averaged to remove random factors due to initialization. For mi-SVM and MI-SVM, we used the same radial base function kernel (RBF) and kernel parameters as our proposed method. For citation-kNN, we include results using 20 citers and 20 references. We evaluated the classification performance of each algorithm using a leave-one-patient-out test scheme. NIH Biowulf computer cluster (http://biowulf.nih.gov/) was utilized for parallel computation. Each test patient used one node of the computer cluster. We compare these methods using ROC analysis. ROC curves are compared using correlated area test statistics calculated with ROCKIT [48].

VI. Experimental Results

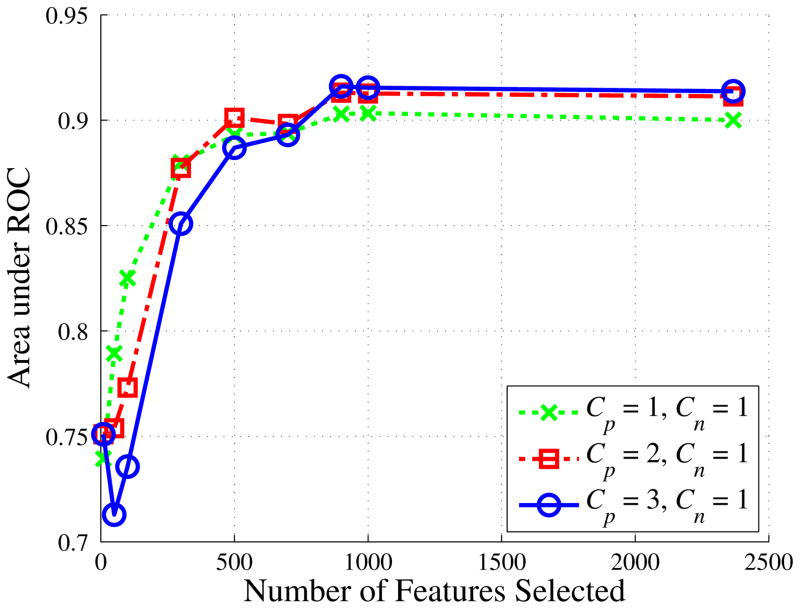
There were 2367 statistical features extracted from each instance (viewpoint). Since we have very high dimensional data, one natural question is that do we really need all these features. To answer this question, we conducted experiments on feature selection using the minimum redundancy and maximum relevance feature selection method (mRMR) [49]. mRMR is a state-of-the-art feature selection method widely used in biomedical research. It selects good features according to the maximal statistical dependency criterion based on mutual information and minimizes the redundancy among features simultaneously. We show areas under the ROC curves (AUC’s) of the proposed method with different number of features selected by mRMR in Fig. 5. We found no very distinctive, discriminant, and independent features. Further, we found that performance of the proposed method stabilizes with more than 900 features, indicating that additional features are not very distinctive. We found no statistical difference between performance when using 900 features and when using the full 2367 features (p = 0.9679).

Fig. 5.

AUC’s of the proposed method when different numbers of features were selected by the minimum redundancy and maximum relevance feature selection method.

In Fig. 5, we also show the effect of the C_p and C_n parameters. When using more than 900 features, performance increased as the C_p/C_n ratio increased. However, the effect was small moving from C_p/C_n=2 to C_p/C_n=3. Because smaller ratios are more computationally efficient, we set C_p=2 and C_n=1 for the remainder of our experiments.

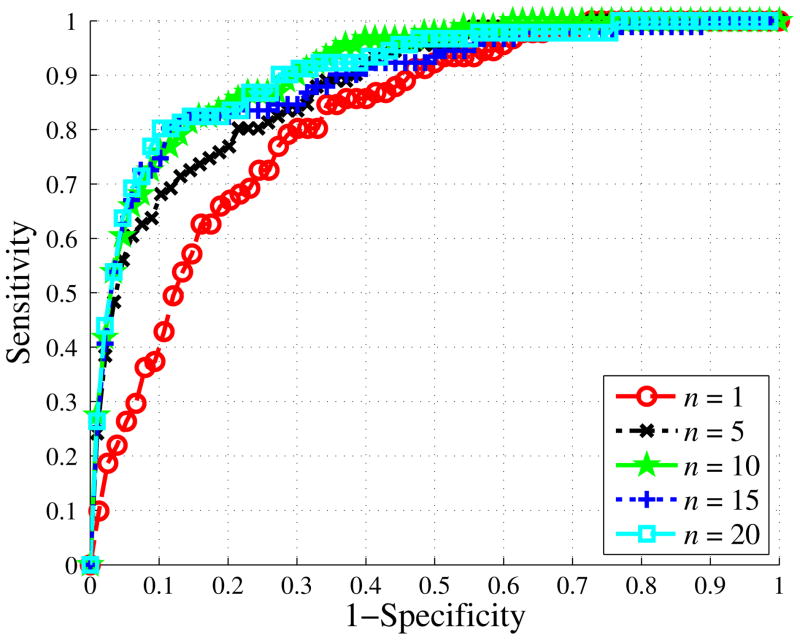
We investigated the impact of the number of instances per bag on the performance of our method. We found improvement as we increased the number of instances per bag from 1 to 10 (Fig. 6). However, we saw no difference in performance when adding additional instances. The AUC’s when using 1, 5, 10 15, and 20 instances were 0.816 (±0.0273), 0.882 (±0.0232), 0.912 (±0.0205), 0.891 (±0.0225), and 0.9083 (±0.0209). We found the performance with 10 instances was significantly greater than the performance using either 1 or 5 instances (p-values < 0.01). We found no significant difference between using 10 and 20 instances (p=0.8250).

Fig. 6.

ROC curves when utilizing various number of instances (n) in each bag. We set k = 900, C_p = 2, and C_n = 1 in constructing each of these curves.

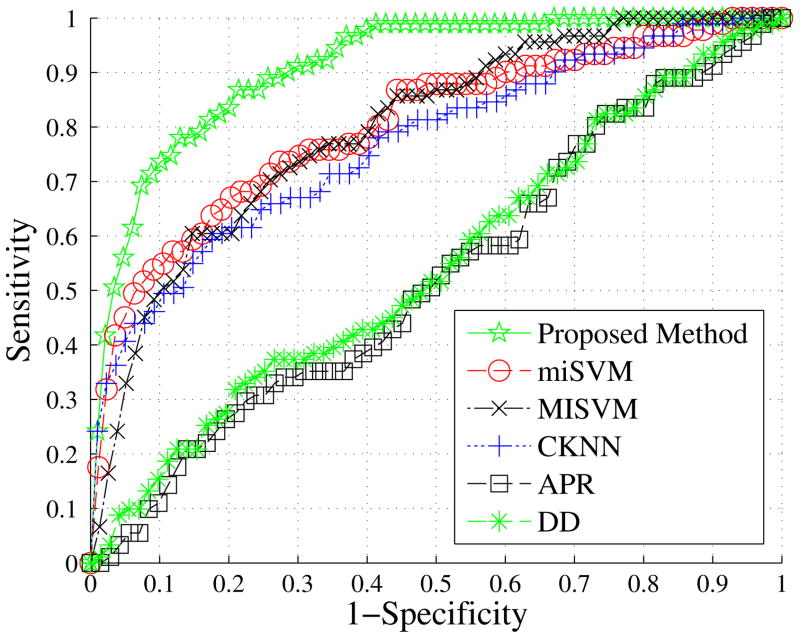
In Fig. 7, we compare the ROC curve of our proposed method with the five methods described in Section V. We utilized all available features for training and testing in this experiment because feature selection is computationally expensive. Our proposed method demonstrates the best performance. For the proposed method, k = 2367, C_p = 2 and C_n = 1. The optimal learned T_p and T_n were all 1. The AUC’s of our proposed method, miSVM, MISVM, CKNN, DD, and APR were 0.911 (±0.0206), 0.802 (±0.0280), 0.795 (±0.0283), 0.769 (±0.0292), 0.523 (±0.0309), and 0.523 (±0.0309), respectively. Since the miSVM and MISVM showed closest performance to our method, we computed correlated area test statistics of those methods with our proposed method. We found a significant difference between our method and the miSVM and MISVM approaches (p-values < 0.001). There was no statistical difference between miSVM and MISVM (p=0.6176).

Fig. 7.

ROC comparisons of the methods. Our proposed method demonstrates the highest performance among various MIL algorithms.

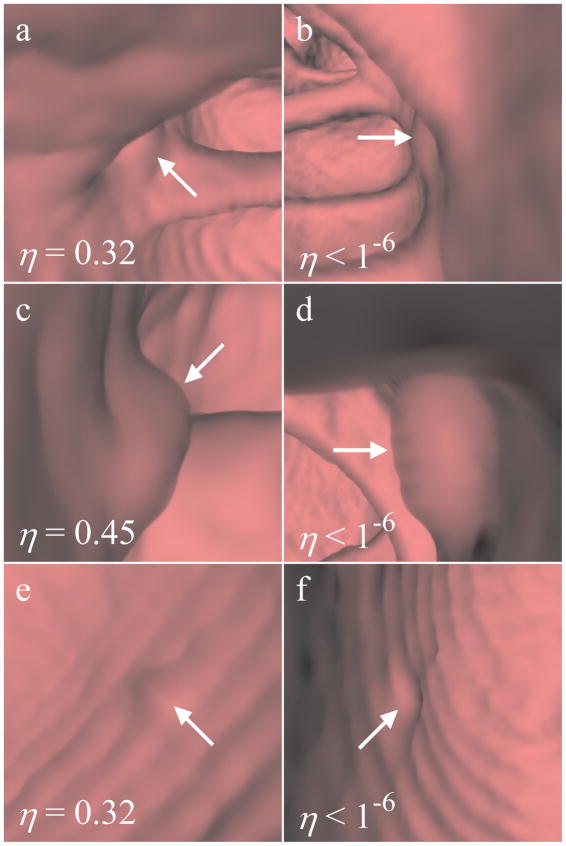
Optimization of η plays a key role in our MIL paradigm. The η values allow us to evaluate the contribution of each frame in a bag. In Fig. 8 we show typical examples of instance ranking. Each row corresponds to one CAD PC. The left and right columns show, respectively, instances with the highest and lowest score based on the ranking η which comes from the solution of the optimization problem (8) and (9). The ranking 1/η is equivalent to the probability that the instance should be chosen for training of the classifier. Instances that are highly ranked by 1/η correspond to support vectors near the decision boundary in our large margin classification paradigm, i.e. these instances possess features that are difficult to correctly classify. For a positive (negative) bag, the highest ranked instance by η should resemble a typical true polyp (false positive) and the lowest ranked instance should have characteristics of false positives (true polyps).

Fig. 8.

Result of instance ranking. Images (a)–(f) are differing perspective views of three true polyp detections from testing video sequences, with images (g)–(l) demonstrating analogous examples of false positive detections. The left column and right column show the highest- and lowest-rated instance for each detection, respectively. The y_i values show the bag labels for the corresponding rows. η is a scalar weighting value assigned to each instance to rank positive (negative) instances in a positive (negative) bag. (a)–(b) 7 mm pedunculated polyp, (c)–(d) 6 mm sessile polyp (same polyp as in Fig. 1a–1b), (e)–(f) 8 mm sessile polyp, (g)–(h) air bubble, (i)–(j) ileocecal valve, and (k)–(l) distorted fold.

In Fig. 8a–8f we show typical examples of instance selection involving three true polyps. In Fig. 8a, the image shows a growth coming off of a fold representative of a true polyp. However, the fold obstructs this polyp in Fig. 8b, so the frame contains no polypoid features. The detection in Fig. 8c–8d is the same detection seen in Fig. 1a–1b. In Fig. 8c the polyp appears as a small circular shape, distinct from the background. However, when the perspective changed, the same polyp is clouded by an imaging artifact (Fig. 8d). It is interesting that the automatic selection is similar to the manual selection in Fig. 1. Please note that we provide only 2D color images to our algorithm, and there is no depth information which can be inferred from a single 2D image. Similarly, the polyp in Fig. 8e–8f is more representative of a true polyp from the viewpoint in Fig. 8e than the viewpoint in Fig. 8f.

In Fig. 8g–8l we show typical examples of instance selection involving three false positive detections. Fig. 8g–8h shows a gas bubble. Both of these images have shapes suggestive of a true polyp. However, the air within the bubble, rendered solid blue, is clearly visible at the center of the image in Fig. 8g while it is obstructed in Fig. 8h. This color information clearly distinguishes the detection as a false positive. In Fig. 8i–8j, we show a common false positive, an ileocecal valve. The perspective on the detection in Fig. 8i lessens the polypoid features of the detection. Similarly, the viewpoint in Fig. 8k gives that detection a less polypoid shape than the viewpoint in Fig. 8l.

In Fig. 9, we show examples of our proposed method’s performance on flat polyps. These flat polyps were identified in the database by a radiologist. Our algorithm showed poor classification performance on the 6 mm polyps in Fig. 9a–9b and Fig. 9e–9f, ranking them in the bottom 20% of all true detections. Judging by the poor visual characteristics of the highest-rated instance, our classifier was unable to find any instances in those bags that were indicative of a polyp. However, the 8 mm flat polyp in Fig. 9c–9d was assigned a score in the upper third of all true polyp detections. This detection had a pronounced shape more indicative of a polyp.

Fig. 9.

Ranked instances of flat polyps. The left column and right column show the highest- and lowest-rated instance for each detection, respectively. (a)–(b) 6 mm flat polyp, (c)–(d) 8 mm flat polyp, (e)–(f) 6 mm flat polyp. The polyps in (a)–(b) and (e)–(f) each had scores in the bottom 20% of all true polyps. The polyp in (c)–(d) had a score in the upper third of all true polyps.

VII. Discussion and Conclusion

In this paper we have described the development and testing of a novel method for colonic polyp detection in CTC using video analysis and MIL techniques. For each CAD mark in CTC, we created a video demonstrating the detection from multiple viewpoints. Classification of the detections in these videos was formulated as a MIL problem. Here, as opposed to traditional MIL theory, a negative bag may contain positive instances, depending on the viewing angles and camera distance to the target. To accommodate for this variation of standard MIL methodology, we developed a novel MIL paradigm maximizing a L2-norm soft margin using semidefinite programming, which can automatically optimize the relevant parameters (η, T_p and T_n). Comparison of results from analysis of a CTC testing set demonstrated statistically higher polyp candidate classification accuracy with the proposed method, compared with those of traditional MIL methods.

From the experimental results, we find that the traditional MIL methods, e.g. Citation KNN, diversity density and axis-parallel rectangle, did not work well with our video classification data set. The key reason is that our problem does not meet the assumptions in traditional MIL paradigm that instances in a negative bag are all negative. The mixed positive and negative instances in positive and negative bags make these traditional MIL methods perform poorly. MISVM and miSVM are also based on the idea of margin maximization making them somewhat more advanced than the traditional MIL methods. However, our proposed method still showed better performance compared with MISVM and miSVM. We attribute this to our use of ranking instances within bags (as our proposed method does) as compared to simply identifying the most representative instance (MISVM), or guessing the label of instances (miSVM). Rankings appear to maximize the information extracted from the video sequences for our particular problem where positive and negative instances are mixed within each bag type.

Regarding computational complexity, SVMs have the complexity of O(kn²) for radial basis function (RBF) kernels and O(kn) for linear kernels, where n and k are number of samples and features, respectively. For our proposed method, since we introduce ranking variable η for each instance, computational complexity will be O(4kn²) and O(2kn) for RBF and linear kernels, respectively. Here n is the total number of instances in the dataset for our MIL problem. While our proposed method is more computationally complex than SVMs, the complexity scales linearly with SVM methods. Since we see significantly higher performance from our method, we feel that the increased complexity is acceptable. The higher performing system may also allow us to loosen our constraints in our initial detection scheme to increase the sensitivity of the CAD system.

The η rankings present an interesting new piece of data for clinicians. As our method seeks to mimic radiologist interpretation, the learned rankings should represent the most diagnostically-relevant viewpoints of a particular CAD mark. By immediately presenting the clinician with the most relevant viewpoints, we could decrease the amount of time required to fully investigate a CAD mark. The η values could also help to narrow the visual search space for clinicians. As is shown in Fig. 8, the η values translate well into relevant visual information. While the generation and analysis of the videos needed by our algorithm will take time (a few minutes for each case), such computations can be done along with the initial processing of the CTC data. We believe that the time savings in identifying the most relevant viewpoints could outweigh the modest increase in computational time.

In our current implementation we chose to only use 10 viewpoints to represent each polyp candidate. This selection was based on our findings in Fig. 6. We noted using more than 10 instances per bag resulted in no improvement in performance, and the processing time scales exponentially when using more instances. The processing time for the entire dataset using 10 instances was around 2.5 hours, while the processing time increased by a factor of 10 to 25 hours when 20 instances were used. Further work could be done to investigate the optimal number of instances to use to represent each detection. Further work could also investigate methods to include up to hundreds of video frames.

Flat polyps present a great challenge in CTC CAD due to their inconspicuitiveness in CT images [50–52]. Usually flat polyps show plaque-like appearance and their heights are less than 3 mm above the colonic mucosa [53]. Traditional 3D image analysis techniques such as curvature analysis show low sensitivity in detection of flat polyps due to their small surface curvature. For our method, flat polyps with small sizes (<=6mm) also prove difficult because the difference between endoluminal renderings of small flat polyps and normal colon inner wall are subtle. For larger flat polyps (>=10 mm), we expect to have higher detection sensitivity since our method can extract texture and boundary shape information of large flat polyps from different view angles and distances. We noted this trend in Fig. 9, where our method did perform better on a larger flat polyp. However, our current dataset only contains 3 flat polyps. In future studies, how to adapt our method to the detection of flat polyps will be an interesting problem and research direction.

Compared with the CH-FD MIL method [25], o u r formulation has several significant differences. First, CH-FD tries to optimize the classifier decision boundary using Fisher’s linear discriminant criterion; whereas our proposed method is based on margin-maximization criterion. Secondly, the definition of bags and instances are different. A positive bag in CH-FD is a collection of candidates spatially close to a positive ground truth mark. That method treats all candidates distant from a positive ground truth mark as negative instances, and it does not formally group these negative instances into bags. In our method, we define instances based on video frames and detections as bags. Lastly, CH-FD utilizes traditional 3D features for medical image analysis while we developed video generation techniques and extracted statistical 2D image features for classification. One advantage of our proposed method is that we can provide radiologists the highest ranked or most representative 3D rendered images for each PC which will aid them in CTC practice. CH-FD and our proposed method work at different levels regarding definition of bags and instances; the combination of the two methods to form a hierarchical MIL learning scheme will be of interest.

In this paper, we computed several groups of features in the feature extraction process. When we computed the kernel, we simply concatenated them into one large (high dimensional) feature vector for the similarity computation. Since different groups of features have different classification ability, it would be interesting in future work to weigh these groups of features for classification by embedding multiple kernel learning into our MIL scheme. The addition of multiple kernel learning would be expected to lead to further improvements in the performance of our system.

Appendix

A. Proof of Theorem 2

Let L(w,b,ξ,α,β) be the Lagrangian of the inner minimization problem in equation (8):

$$\begin{array}{l}L(\mathbf{w},b,\mathbf{\xi },\mathbf{\alpha },\mathbf{\beta })=\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C_p\sum _{i=1}^{n_p}\frac{{\xi }_i^2}{{\eta }_i}+C_n\sum _{i=n_p+1}^n\frac{{\xi }_i^2}{{\eta }_i}\\ -\sum _{i=1}^n{\alpha }_i\left(y_i\left({\mathbf{w}}^T\phi ({\mathbf{x}}_i)+b\right)-1+{\xi }_i\right)+\sum _{i=1}^n{\beta }_i{\xi }_i,\\ {\alpha }_i\ge 0,{\beta }_i\ge 0,i=1,2,\dots ,n.\end{array}$$ (14)

where α ∈ ℝⁿ and β ∈ ℝⁿ are auxiliary variables introduced for the dual problem. The dual problem is:

$$\begin{array}{l}\underset{\mathbf{\alpha }}{max}{\mathbf{\alpha }}^T\mathbf{e}-\frac{1}{2}{\mathbf{\alpha }}^T\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C_p}\left(\begin{array}{cc}\mathit{diag}({\mathbf{\eta }}_p)& 0\\ 0& 0\end{array}\right)+\frac{1}{C_n}\left(\begin{array}{cc}0& 0\\ 0& \mathit{diag}({\mathbf{\eta }}_n)\end{array}\right)\right)\mathbf{\alpha },\\ s.t.{\mathbf{\alpha }}^T\mathbf{y}=0,C_p\ge {\alpha }_i\ge 0i=1,2,\dots ,n_p,C_n\ge {\alpha }_i\ge 0i=n_p+1,\dots ,n.\end{array}$$ (15)

So the problem shown in (8) can be converted to the following problem:

$$\begin{array}{l}\underset{\mathbf{\eta },T_p,T_n}{min}\underset{\mathbf{\alpha }}{max}{\mathbf{\alpha }}^T\mathbf{e}-\frac{1}{2}{\mathbf{\alpha }}^T\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C_p}\left(\begin{array}{cc}\mathit{diag}({\mathbf{\eta }}_p)& 0\\ 0& 0\end{array}\right)+\frac{1}{C_n}\left(\begin{array}{cc}0& 0\\ 0& \mathit{diag}({\mathbf{\eta }}_n)\end{array}\right)\right)\mathbf{\alpha },\\ s.t.\mathbf{0}<\mathbf{\eta }\le \mathbf{1},{\mathbf{A}}_p{\mathbf{\eta }}_p\le T_p\mathbf{e},{\mathbf{A}}_n{\mathbf{\eta }}_n\le T_n\mathbf{e},T_p\le 1,T_n\le 1,\\ {\alpha }^{T}y=0,C_p\ge {\alpha }_i\ge 0i=1,2,\dots ,n_p,C_n\ge {\alpha }_i\ge 0i=n_p+1,\dots ,n.\end{array}$$ (16)

The inner maximization problem shown above could be achieved at

$${\mathbf{\alpha }}_{max}={\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C_p}\left(\begin{array}{cc}\mathit{diag}({\mathbf{\eta }}_p)& 0\\ 0& 0\end{array}\right)+\frac{1}{C_n}\left(\begin{array}{cc}0& 0\\ 0& \mathit{diag}({\mathbf{\eta }}_n)\end{array}\right)\right)}^{-1}\times (\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y}),$$ (17)

where μ ∈ ℝⁿ and ε ∈ ℝ are auxiliary variables introduced for the dual problem. By using Schur complement lemma, we get following SDP problem:

$$\begin{array}{l}\underset{\mathbf{\eta },T_p,T_{n,}\mathbf{\mu },\epsilon }{min}\delta s.t.\left(\begin{array}{cc}\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C_p}\left(\begin{array}{cc}\mathit{diag}({\mathbf{\eta }}_p)& 0\\ 0& 0\end{array}\right)+\frac{1}{C_n}\left(\begin{array}{cc}0& 0\\ 0& \mathit{diag}({\mathbf{\eta }}_n)\end{array}\right)& (\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})\\ {(\mathbf{e}+\mathbf{\mu }+\epsilon \mathbf{y})}^T& 2\delta \end{array}\right)\ge 0.\\ \mathbf{0}<\mathbf{\eta }\le \mathbf{1},{\mathbf{A}}_p{\mathbf{\eta }}_p\le T_p\mathbf{e},{\mathbf{A}}_n{\mathbf{\eta }}_n\le T_n\mathbf{e},T_p\le 1,T_n\le 1,\mathbf{\mu }\ge \mathbf{0}.\end{array}$$ (18)

B. Proof of Proposition 1

By using Lagrange multipliers optimization method, we transferred the constrained optimization problem (1) into the following unconstrained primal Lagrange function:

$$L_p^2(\mathbf{w},\mathbf{\xi },\mathbf{\alpha },\mathbf{\beta })=\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+\frac{C}{2}\sum _{i=1}^n\frac{{\xi }_i^2}{{\eta }_i}+\sum _{i=1}^n{\beta }_i\left(-1\times {\xi }_i\right)+\sum _{i=1}^n{\alpha }_i\left(1-{\xi }_i-y_i\left({\mathbf{w}}^T\phi \left({\mathbf{x}}_i\right)+b\right)\right)$$ (19)

The Karush-Kuhn-Tucker (KKT) conditions for optimal w, b and ξ are:

$$\begin{array}{l}\frac{\partial L_p^2}{\partial \mathbf{w}}=\mathbf{w}-\sum _{i=1}^n{\alpha }_i{y}_i\phi ({\mathbf{x}}_i)=0,\\ \frac{\partial L_p^2}{\partial b}=-\sum _{i=1}^n{\alpha }_i{y}_i=0,\\ \frac{\partial L_p^2}{\partial {\xi }_i}=C{\eta }_i{\xi }_i-{\beta }_i-{\alpha }_i=0,\\ y_i\left(w^T\phi ({\mathbf{x}}_i)+b\right)-1+{\xi }_i\ge 0,{\beta }_i{\xi }_i=0,\\ {\alpha }_i\ge 0,i=1,2,\dots ,n.\end{array}$$ (20)

By using KKT conditions, we can remove primal variables and get dual representation of optimization problem (1):

$$\begin{array}{l}\underset{\mathbf{\eta }}{min}\underset{\mathbf{\alpha }}{max}{\mathbf{\alpha }}^T\mathbf{e}-\frac{1}{2}{\mathbf{\alpha }}^T\left(\mathbf{K}\circ {\mathbf{yy}}^T+\frac{1}{C}\mathit{diag}(\mathbf{\eta })\right)\mathbf{\alpha }\\ s.t.\mathbf{\alpha }\ge \mathbf{0},{\mathbf{\alpha }}^T\mathbf{y}=0,\mathbf{0}<\mathbf{\eta }\le \mathbf{1},\mathbf{A}\mathbf{\eta }\le T\mathbf{e},\end{array}$$ (21)