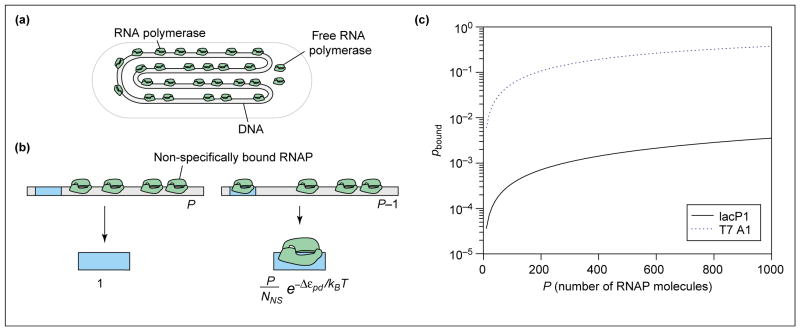
Figure 1.

Probability of promoter occupancy (a) Schematic showing how, in the simple model, the DNA molecule serves as a reservoir for the RNAP molecules, almost all of which are bound to DNA. (b) Illustration of the states of the promoter – either with RNAP not bound or bound and the remaining polymerase molecules distributed among the non-specific sites. The statistical weights associated with these different states of promoter occupancy are also shown. (c) Probability of binding of RNAP to promoter as a function of the number of RNAP molecules for two different promoters. We assume the number of non-specific sites is N_NS = 5 × 10⁶, and calculate the binding energy difference using the simple relation $\mathrm{\Delta }\epsilon pd=k_{B}Tln(K_{pd}^S/K_{pd}^{NS})$, where the equilibrium dissociation constants for specific binding ( $K_{pd}^S$) and non-specific binding ( $K_{pd}^{NS}$) are taken from in vitro measurements. In particular, making the simplest assumption that the genomic background for RNAP is given only by the non-specific binding of RNAP with DNA, we take $K_{pd}^{NS}=10000\text{nM}$ [37], for the lac promoter $K_{pd}^S=550\text{nM}$ [38] and for the T7 promoter, $K_{pd}^S=3\text{nM}$ [39]. For the lac promoter, this results in Δε_pd = −2.9k_BT and for the T7 promoter, Δε_pd = −8.1k_BT.