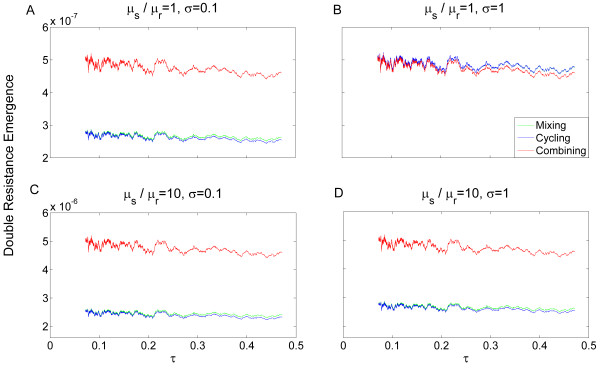
Figure 3.

Robustness of the dynamics describing resistance acquisition by mutation. The dynamics describing double resistance emergence by mutation were studied for 10⁴ random sets of parameters (derived from the distributions described in the main text). The moving average of the emergence of double resistance (see methods) is plotted as a function of the rate of clearance due to antibiotic usage (τ). Note that the same data sets are used for a given value of τ under each of the three strategies, generating an association between the curves. The moving average of mixing is plotted in green, of cycling in blue, and of combining in red. When the values of the moving average for mixing and cycling are very close only the blue curve is visible. (A) $\frac{{\mu }_s}{{\mu }_r}$ = 1, σ = 0.1. When σ is low, cycling decreases the emergence of double resistance better than the other strategies even with no influence of stress on mutation rates. (B) $\frac{{\mu }_s}{{\mu }_r}$ = 1, σ = 1. When σ is high and stress has no effect on mutation, combining is more efficient than the other strategies. (C) $\frac{{\mu }_s}{{\mu }_r}$ = 10, σ = 0.1. At low σ, increased influence of stress on mutation rates results in increased emergence by about an order of magnitude (compare with A), where cycling remains the most efficient strategy. (D) $\frac{{\mu }_s}{{\mu }_r}$ = 10, σ = 1. At high σ, increase in mutation rates due to stress alters the preferred strategy drastically from combining to cycling (compare with B).