Log-scale Dose Response of Inhibitors on a Chip

Abstract

We demonstrate the accommodation of log-scale concentration gradients of inhibitors on a single microfluidic chip with a semi-direct dilution capability of reagents for the determination of the half-inhibitory concentration or IC₅₀. The chip provides a unique tool for hosting a wide-range of concentration gradient for studies that require an equal distribution of measuring points on a logarithmic scale. Using Matrix metalloproteinase IX and three of its inhibitors, marimastat, batimastat and CP471474, we evaluated the IC₅₀ of each inhibitor with a single experiment. The present work could be applied to the systematic study of biochemical binding and inhibition processes particularly in the field of mechanistic enzymology and the pharmaceutical industry.

Introduction

In the process of drug discovery, quantitative characterization of inhibitory potencies of all the potential drug candidates is necessary to figure out the best candidate¹. For comparing potential drug candidates an outcome of curvefitting of a sigmoidal curve to the dose response data or the value of half maximal inhibitory concentration, IC₅₀ is used^2-4. Inhibitors are small molecular weight molecules that impede the substrate molecules from reaching or binding to the enzyme active sites⁵ and half of today's drugs are inhibitors¹. In dose response analysis the use of a log-scale concentration range is important because the dose response is represented by a Maltusian-type differential equation whose solution is logarithmic type⁶. Recently, the importance of a log scale for drug response analysis, based on thermodynamical basis, has been reiterated ⁷. The drug response is directly proportional to the log of the drug concentration expressed as μ = RT ln[a]⁸, where μ is chemical potential or response of the drug and a is activity or concentration of the drug. Hence, care has to be taken to select drug concentrations that are equally spaced using a logarithmic scale instead of a linear scale.

Conventionally, in the determination of IC₅₀, serial dilutions, with test tubes, vials and micro-plates, are routinely used for the preparation of a concentration gradient⁹. However, it is well known that the serial dilution method introduces ample errors through pipetting that directly affect the precision of each dilution ratio. Considering the required multiple steps of dilution for the realization of wide concentration ranges to obtain dose response data, the error in each step of serial dilution could lead to compounding of errors after several steps of serial dilution. This could affect the evaluation of IC₅₀ values of drug candidates and their realistic comparisons. Therefore, for the evaluation of IC₅₀ , direct dilution of drugs has been recommended¹⁰. During the last two decades, several studies on enzymatic reactions based on microfluidic formats have been reported^11-16. The first study of enzyme inhibition on a glass chip with electrokinetic control was demonstrated by Hadd et al¹⁶. The enzyme, substrate and inhibitor were mixed at a four-way interaction of microchannels and only one reaction condition was examined without concentration gradient. A centrifugal microfluidic system with forty-eight parallel microchannel structures was shown by Duffy et al¹³. Because internal metering is not possible with centrifugal system in general, extra steps of off-chip concentration gradient were required to generate different reaction conditions. Few recent integrated microfluidic platforms^17,18 have shown the capability of conducting multi-step and parallel reactions with limited and narrow ranges of concentration gradients. Droplet-based microfluidic systems^19-21 have been applied to enzymatic reactions ^12,18,22 and shown the possibility of parallel experiments with flexible concentration gradients¹⁸.

However, wide ranges of concentration gradients to test dose responses are still remained challenging. Recently, several commercial platforms ^10,23-26 have been reported for dose response reactions using micro-titer plates and a special ejector, a piezo dispenser ^23,24 or an acoustic droplet ejector^25,26. Since the micro-titer plate is operated in an open environment, the evaporation of reagents and subsequent volumetric errors are of significant concerns at nano- or pico-liter scales²⁷. In addition, at a given time, an ejector or a dispenser can be addressed only to a single micro well for dispensing a reagent. Therefore, the simultaneous operations of delivery, metering, gradient formation, mixing and the detection are extremely challenging for all the micro wells.

Here, we present a new approach for dose response analysis of enzyme inhibitors by using an integrated microfluidic system that has the capability of realizing a log-scale concentration gradient on a chip through semi-direct dilution of samples. To demonstrate the function of the present system, by conducting a series of dose response reactions in log-scale concentration gradients with nanoliters of drug or inhibitor samples, we measured dose response curves and determined IC₅₀ values of three inhibitors, marimastat, batimastat and CP471474 for matrix metalloproteases-9 (MMP-9) and MMP substrate III.

Materials and methods

Materials

The substrate QXL™520-Pro-Leu-Gly-Cys-(Me)-His-Ala-D-Arg-Lys-(5-carboxy-fluorescein)-NH₂ (AnaSpec Inc), internally quenched peptide matrix of matrix metalloproteinases-9 (MMP-9) was used for the enzyme reaction. This substrate releases fluorescent signals through dissociation of the quencher (QXL™520) and carboxyfluorescein (FAM), fluorophore, via proteolytic cleavage by enzymatic reaction. MMP-9 is known to directly or indirectly influences human diseases, such as infiltration and metastasis of cancer cell, arthritis, etc., hence, MMP-9 is one of the major targets for development of anticancer drugs^28,29. For establishing a standard curve, we used reference dye, FAM-Pro-Leu-OH. The excitation and emission wavelengths for FAM are 480 nm and 520 nm, respectively. According to the enzyme reaction types, 50nM, 10 nM, and 5 nM of MMP-9 were separately dissolved into the reaction buffer (TCNBT; 50 mM Tris, 10 mM CaCl₂, 150 mM NaCl, 0.05% Brij-35, 0.05 % Tween-20 and 0.1% BSA at pH 7.5). For the substrate of MMP, a stock solution was prepared as 100 μM in TCNBT buffer. Inhibitors of MMP-9, marimastat and batimastat (Tocric bioscience), were dissolved into DMSO in 10 mM of stock solution. Prepared reagents were stored at -20°C until dilution with TCNBT buffer for experiment.

Device operation

As shown in Figure 1a and Supporting Figure S1, three (3) gradient formers (GF) with 14 parallel processes on a single chip. Each GF is composed of four (4) microfluidic processors, respectively. Two extra processors are added for a positive control and a negative control on the present chip. A step-by-step operation of the device is depicted in the Figure 1b. The step-by-step operation includes loading and metering of the reagents (substrate, buffer, inhibitor, and an enzyme), mixing of the metered reagents, and the scanning of the reactions. We introduced reagent 1 (substrate, FAM or inhibitor) and 2 (dilution buffer) into their respective inlet channels by applying the pressure from nitrogen gas. The inlet channels were connected to the metering channel for generating the concentration gradients. The third reagent, in this case enzyme, was filled into the enzyme part of the mixer through the reagent 3 inlet channel. The metered reagents 1 and 2 are introduced into the mixer. Now, we have all the three reagents, dilution buffer, substrate and the enzyme solution, in the mixer together maintaining complete contact of the enzyme and the diluted substrates by keeping the mechanical valves closed firmly. In this step, the two reagents were separated from the third reagent in the microreactors by two separation valves to avoid undesirable initiation of the enzyme reactions. We closed all the separation valves around the microreactor, and then opened the two separation valves between the enzyme solution (right side) and the diluted substrate (left side). The three reagents were mixed in the microreactor with sequential operation of the microvalves for peristalsis.

Figure 1.

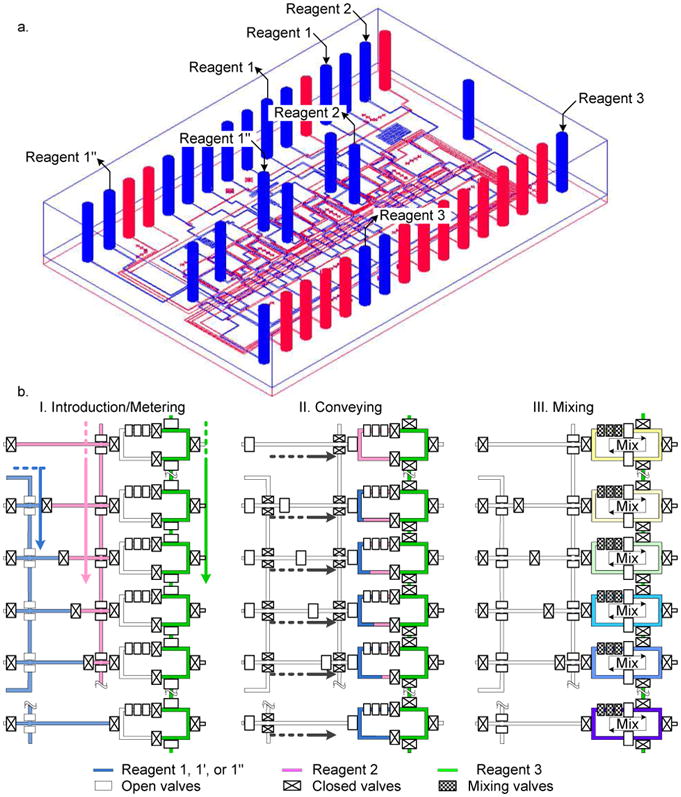
Design and operation of the microfluidic device. (a) 3D view of the chip. The chip is composed of three (3) different gradient formers (GF) with four microfluidic processors for each GF. Two extra processors are added for a positive and a negative controls resulting in 14 parallel reactions at the same time. (b) Step by step operation of single GF. Although a GF is composed of four reactors positive and negative controls are explained together.

Image acquisition and data processing

We used a modified biochip scanner (arrayWoRx®, Applied Precision, WA) to acquire the images of the on-chip dose response reaction. We conducted multiple scans of the part of the chip during the progress of the enzyme reactions. All the acquired images were 16-bit grayscale, the resolution was 7,800 pixels per inch (PPI), and the pixel size was 3.25 μm. To reduce scanning time and ensure enough chip areas for data acquisition, we scanned a partial region of the fourteen microreactors (30.5 mm × 1.5 mm) as shown in Figure 2 bottom. Image acquisition software (arrayWoRx 2.5 Software Suit, Applied Precision, WA) generated the integrated scan image. The total scanning time of the integrated image (30.5 mm × 1.5 mm) was approximately 45 sec. Time series analyzer module of ImageJ software (http://rsb.info.nih.gov/ij/) was used to analyze and digitize all the fluorescence images. We measured the changes in the fluorescent intensity over multiple scanning processes for evaluating the photobleaching rate of FAM on the chip and corrected the digitized data. The loss of fluorescent intensities was compensated by using a similar method used for the photobleaching effect on a multiple scanned confocal image³⁰.

Figure 2.

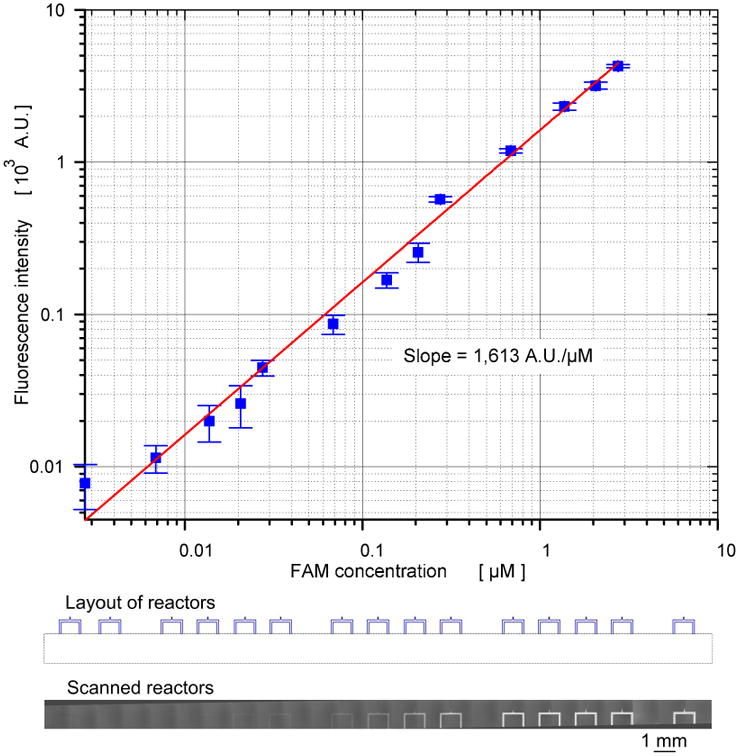
Log-log scale standard curve for FAM with the scanned image of FAM concentration gradients.

Statistical analysis

To determine the kinetic parameters, K_M and k_cat, the initial velocities of the individual reactions were curve-fitted with the Michaelis-Menten equation⁵ using the enzyme kinetics module of Sigmaplot software (Systat software Inc.). For IC₅₀ values with standard error, and 95% confidence interval, we curve-fitted the four parameter nonlinear-logistic-regression model available to the inhibition data. The four parameter model is of the form² as shown below.

$$\%I=\%I_{\text{min}}+\frac{\%I_{\text{max}}-\%I_{\text{min}}}{1+{10}^{\left(\text{Log}\left({\mathit{\text{IC}}}_{50}\right)-\left[I\right]\right)·h}}$$

Where, IC₅₀ refers to median point of the concentration-response plot; [I] represents the concentration of inhibitor; h is the Hill coefficient or Hill slope, which means the steepness of dose-response plot; %I designates percentage inhibiting potency, including minimum and maximum.

Results and discussion

Logarithmic gradient formation

In the present device, each GF has two separate inlets for inhibitor (reagent 1) and buffer (reagent 2). The three identical GFs allow conducting three repetitive experiments with fixed concentration range if we feed an inhibitor and reagent with the same concentrations. For example, if we introduce 10× inhibitor (reagent 1) and 1× working buffer (reagent 2), we can create final inhibitor concentrations of 1×, 2.5×, 5× and 7.5×. We can also derive a wider concentration range from the device by feeding different concentrations of inhibitor (reagent 1) in the three GFs, and by keeping the same concentration of working buffer. If we feed 10× inhibitor to the first GF1, 100× to the GF2, then 1000× to the GF3, the effective concentrations in each GF will respectively be 1, 2.5, 5, 7.5×, for GF1; 10, 25, 50, 75×, for GF2; 100, 250, 500, 750×, for GF3. Here the negative and positive control processors generate 0 and 1000× concentrations. Therefore, by introducing the three concentrations of inhibitor and buffer, meaningful log-scale concentrations for dose response are generated such as 0, 1, 2.5, 5, 7.5, 10, 25, 50, 75, 100, 250, 500, 750 and 1000× by the present device in semi-direct dilution. However, the concentration range could easily be increased by changing the input concentration of inhibitor while keeping buffer the same. In our experiments, as described in Table 1, we have created a concentration range from 1× to 4000× by using 10×, 200× and 4000× of inhibitors for the three GFs. Note that the individual microfluidic processors has nano-liters scale volume. Hence large amount of samples could be saved during dose response analysis in comparison to the large amount of reagent volumes used in conventional methods^10,24,31-33.

Table 1.

Compositions and concentrations of reagents introduced into an integrated microfluidic chip to accommodate a log-scale gradient.

	GFs	Reagents introduced into metering channels		Constant reagent	Final concentractions of metered reagents			Relative concentration rangesb
		Reagent 1	Reagent 2	Reagent 3
[FAM] gradient [nM]	GF1	5000		buffer	2,500.00	~	250.00	1 - 1,000
	GF2	500			187.50	~	25.00
	GF3	50			18.75	~	2.50
[E] gradient [nM]	GF1	20.0	buffer	50 μM substrate in buffer	10.00	~	1.00
	GF2	2.0			0.75	~	0.1
	GF3	buffer				0
								1-100
[S] gradient [μM]	GF1	100.0		5 nM MMP-9 in buffer	50.00	~	5.00
	GF2	10.0			3.75	~	0.50
	GF3	buffer				0
[Marimastat] [nM]	GF1	500.00a			250	~	25
	GF2	25.00a			9.375	~	1.250
	GF3	1.25a			0.469	~	0.063
[CP 417474] [nM]	GF1	2,000.00a	44.3 μM substrate in buffer	10 nM MMP-9 in buffer	1,000	~	100	1 - 4,000
	GF2	100.00a			37.5	~	5
	GF3	5.00a			1.875	~	0.25
[Batimastat][nM]	GF1	500.00a			250	~	25
	GF2	25.00a			9.375	~	1.250
	GF3	1.25a			0.469	~	0.063

^aInhibitor solutions included 44.3 μM substrate

Ranges and concentrations were calculated with 13 microfluidic processors excluding a negative control

To confirm the generation of a logarithmic gradient using present microfluidic chip, we generated the concentration gradient of carboxyfluorescein (FAM) in the ratio of 1:1,000. To generate this concentration gradient, we introduced FAM with three concentrations, 0.05 μM, 0.5 μM, and 5 μM, into the reagent input ports of GF1, GF2, and GF3, respectively. The reaction buffer with a fixed concentration was also introduced to dilution buffer input ports of GF1, GF2 and GF3 (Figure 1 and Figure S1). Therefore, a concentration gradient range of 0.0025 μM to 2.5 μM was generated inside the fourteen (14) microfluidic processors. Figure 2a shows the standard curve for FAM established from 3 independent experiments conducted with log-scale gradients on a chip. In the standard curve, we observed a linear relationship, with a slope of 1,631 AU/μM, between concentration of FAM and the corresponding fluorescence intensity.

Determination of kinetic parameters of enzyme reactions

The half maximal inhibitory concentration, IC₅₀ can be influenced by analysis conditions, such as pH, ionic strength, substrate concentration, etc¹. Among these factors the most dominant factor influencing IC₅₀ value is the [S]/K_M ratio³. For the determination of IC₅₀ value from a logistic-dose response curve the selection of substrate concentration equal to the value of K_M is recommended¹. Therefore, we first determined the K_M value for matrix metalloproteinase-9 (MMP-9) before measurement of the inhibiting potency of the inhibitors.

For the determination of reliable values of IC₅₀ and K_M, selecting the concentration of enzyme that shows linear reaction progress is critical. To decide the enzyme concentration only part of the microfluidic chip was used. We introduced enzyme solutions of 2 nM and 20 nM to GF1 and GF2 to form an enzyme concentration gradient in the range of 0.1 nM ~ 10 nM (1:100) (Figure S2b). (We did not use the group GF3 because concentration of enzyme over 10 nM was not required.) When 50 μM of MMP substrate III was used, it was observed that even with a measuring time of 120 minutes, the kinetic reaction did not reach the plateau for enzyme concentrations as high as 10 nM (Supplementary Figure S3a). Therefore, 10 nM of enzyme concentration was chosen to determine reaction velocities for further kinetic analysis.

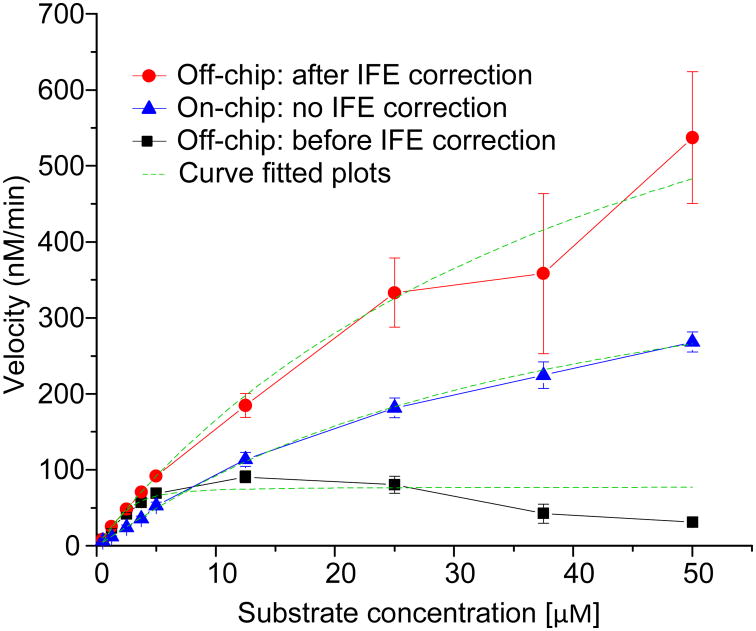
To determine the kinetic parameters, K_M and k_cat, of MMP-9, we introduced 100 μM substrate for GF1 and 10 μM for GF2, respectively, along with the dilution buffer and 20 nM MMP-9 enzyme (Figure S2c). We did not use the GF3 for generating concentration gradient. As a result, 1 μM ~ 100 μM (1:100) of substrate concentration gradient was formed on the chip in the metering channels. After mixing the metered substrate and enzyme into the reactor mixer, the substrate concentration gradient becomes 0.5 μM ~ 50 μM in 9 processors (GF1, GF2 and positive control). Figure S3b shows the results of 9 independent reactions. From this plot it is observed that the rate of reaction increased with the increase of substrate concentration. The reaction rates were linear upto 10 minutes (see Figure S3b box). Therefore, the initial reaction velocity was calculated from these linear parts of the progress curves. A Michaelis-Menten plot was prepared from the initial velocity data of three repetitive experiments (Figure 3). Applying nonlinear curve-fitting to the plot, we determined K_M and k_cat from the on-chip experiments and the respective values were 53.4 ± 5.2 μM and 55.8 ± 4.1 /min. For comparison, we conducted three off-chip experiments and the values of K_M and k_cat are 41.2 ± 4.7 μM and 84.9 ± 0.9/min. The deviation between on-chip and off-chip K_M values was 25.8 % whereas k_cat was 41.3 %. This discrepancy could be attributed to the characteristics of fluorescence detection that is relevant especially at higher substrate concentration with large optical pathlength^5,34-38. Unlike absorbance based measurement the fluorescence detection experiences significant loss of fluorescence intensity at higher substrate concentrations, known as the inner filter effect (IFE)^5,39. The correction factors are used to compensate for the loss of florescence intensity. However, the correction factors exponentially increase with the increase of substrate concentrations^35,38,40. On the other hand, in our on chip experiments, we observed negligible saturation of fluorescence intensity under the same substrate concentration range (Figure 3). We assume that these differences are due to different length of optical path for on-chip, ~ 10 μm, and off-chip, ~ 5 mm, experiments. In addition to the fact that an enzyme is an biological sample with variable properties⁴¹.

Figure 3.

Determination of enzyme kinetic parameters, K_M and k_cat. Comparison of on-chip and off-chip results indicates no need of inner filter effect correction factor for on-chip data. The off-chip velocities, after applying correction factor, shows marked improvement in the velocities at each substrate concentration. The error bar is obtained from three individual experiments. The exponential nature of corrector factor increases the magnitude of error bar, especially at higher substrate concentrations in corrected off-chip velocity data.

Assessment of inhibition potencies

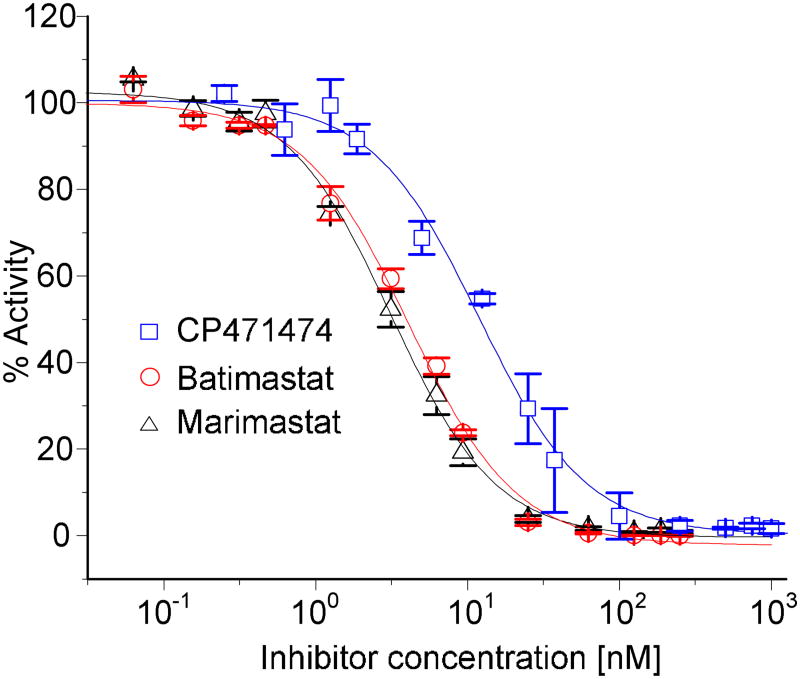
To show the ability of our device to generate a logarithmic concentration gradient and the functionality of our device to conduct logistic dose response studies, we determined the IC₅₀ values of three inhibitors, marimastat, batimastat and CP417474, of the MMP-9 enzyme from their corresponding logistic dose response plots. Inhibitor concentration ranges of 0.063 nM ~ 250 nM (1:4000) for marimastat and batimastat and 0.25 nM ~ 1,000 nM for CP417474 were created on the chip in the 14 reactors. Note that, all the 14 reactors were used considering the requirement of a wider concentration range of inhibitors (Figure 1, Figure S1 and Figure S2), 22.15 μM of substrate and 5 nM of enzyme was used, respectively. Figure 4 shows dose response plots for the 3 inhibitors, marimastat, batimastat and CP417474. From these plots, the IC₅₀ values for marimastat, batimastat and CP417474 are 3.2 ± 0.2 nM, 4.1 ± 0.2 nM and 11.9 ± 1.0 nM, respectively. The respective IC₅₀ values from our off-chip experiment are 3.1 ± 0.1 nM (marimastat), 3.5 ± 0.3 nM (batimasat) and 14.9 ± 0.9 nM (CP417474). From the literature, the reported IC₅₀ values for marimastat and batimastat are 3 nM^42,43 and 3-4 nM^44,45, respectively. Through the comparison of the results from on-chip experiment and off-chip experiment, we observed the deviation of 3.2 %, 17 % and 20 % in the IC₅₀ values of marimastat, batimastat, and CP417474 inhibiters, respectively. These deviations in the values of IC₅₀ are acceptable, considering enzyme as a biological sample with variable properties⁴¹. Therefore, the present microfluidic chip can provide reliable determination of IC₅₀ values of inhibitors with the automation of sample preparation, gradient generation, mixing, incubation and optical detection.

Figure 4.

The logistics dose response plots for three inhibitors, marimastat, batimastat and CP471474, of MMP-9 enzyme. The dose-response plot for each inhibitor was obtained from three on-chip experiments. The IC₅₀ values for each inhibitor were calculated by curvefitting the four parameter model to the inhibitory activity data.

The present device can be used for the concentration-response analysis of reagents where a logarithmic scale concentration gradient is required. Our device could be used for various applications where log-scale gradient with flexibility of concentration range is required. The present system for example could be used for the evaluation of EC₅₀, LD₅₀ and LC₅₀ by applying to microbial cells or animal cells or for conducting cell cytotoxicity assays. These dose-response or cytotoxicity experiments could be conducted by feeding the cells to the constant volume part of the mixer and forming the gradient of inhibitors or reagent, for which the toxicity limit is to be determined, in a group of reactors.

Conclusions

In conclusion, we demonstrated a new approach of implementing log-scale concentration gradient with an integrated microfluidic chip that has semi-direct dilution capability of reagents in addition to metering and mixing of reagents with 14 parallel microfluidic processors. We showed that the concentration range from 1:0 to 1:4000 of two reagents is accommodated on the present system. We successfully determined IC₅₀ values of three inhibitors of marimastat, batimastat and CP417474 for MMP-9 enzyme from the corresponding logistic dose response plots of each inhibitor with a single on chip experiment. We also confirmed that with our nanoliter-scale fluidic system inner filter effect that is common with high substrate concentrations with conventional cuvettes is avoided. We believe that the new device would be a useful tool for pharmaceutical sciences especially for the evaluation of IC₅₀ of various compounds through systematic handling of reagents in nanoliter scale.