Fig. 1.

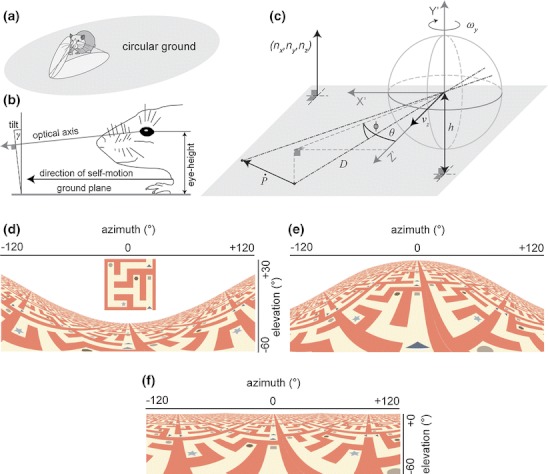
Our model for visual image motion of a rat. (a) A virtual rat is simulated running along recorded trajectories (Hafting et al. 2005). Optic flow is modeled for the overall visual field, which includes left and right hemisphere. (b) Shows the eye-height h and tilt angle γ of the optical axis with respect to the ground; adapted and redrawn from Adams and Forrester (1968), their Figure 6. (c) Visual image motion is generated for sample points P on the ground as the rat is moving parallel to the ground or rotating around an axis normal to the ground. This drawing is for γ = 0 ° tilt and, thus, the linear velocity is along the optical axis and the rotational velocity around the y-axis (yaw). (d-f) Projections of a regular labyrinth texture (inset in d) tiled on the ground floor within ±120 ° azimuth and ±60 ° elevation using the spherical camera model. The nodal point of the spherical camera is h = 3.5 cm above the ground plane 120 x 120 cm large and is placed in the center of the plane. Tilt angle varies, in (d) it is γ = -30 °, in (e) γ = 30 °, and in (f) γ = 0 °. All three images were rendered with Persistence of Vision Pty. Ltd. (2004). Note that the labyrinth texture does not coincide with some maze-task but has only been chosen for visualization purposes. Instead the simulated rat can freely move on a ground platform