Mechanics of myosin function in white muscle fibres of the dogfish, Scyliorhinus canicula

Abstract

The contractile properties of muscle fibres have been extensively investigated by fast perturbation in sarcomere length to define the mechanical characteristics of myofilaments and myosin heads that underpin refined models of the acto-myosin cycle. Comparison of published data from intact fast-twitch fibres of frog muscle and demembranated fibres from fast muscle of rabbit shows that stiffness of the rabbit myosin head is only ∼62% of that in frog. To clarify if and how much the mechanical characteristics of the filaments and myosin heads vary in muscles of different animals we apply the same high resolution mechanical methods, in combination with X-ray diffraction, to fast-twitch fibres from the dogfish (Scyliorhinus canicula). The values of equivalent filament compliance (C_f) measured by X-ray diffraction and in mechanical experiments are not significantly different; the best estimate from combining these values is 17.1 ± 1.0 nm MPa⁻¹. This value is larger than C_f in frog, 13.0 ± 0.4 nm MPa⁻¹. The longer thin filaments in dogfish account for only part of this difference. The average isometric force exerted by each attached myosin head at 5°C, 4.5 pN, and the maximum sliding distance accounted for by the myosin working stroke, 11 nm, are similar to those in frog, while the average myosin head stiffness of dogfish (1.98 ± 0.31 pN nm⁻¹) is smaller than that of frog (2.78 ± 0.30 pN nm⁻¹). Taken together these results indicate that the working stroke responsible for the generation of isometric force is a larger fraction of the total myosin head working stroke in the dogfish than in the frog.

Key points

• Muscle force and shortening are generated by a structural change called the working stroke in myosin motor proteins that cross-link the myosin and actin filaments in muscle.

• Precise values for two key parameters of the myosin motor – its mechanical stiffness and the size of the working stroke at low load – were previously only available from one type of muscle in one species, fast twitch muscles of the frog, so it was not clear how generally applicable these values were.

• We show that in dogfish fast muscle the low-load working stroke is the same as in frog muscle, but the myosin motor stiffness is smaller.

• The results provide new insights into how the molecular properties of myosin motors in different muscle types and species may be adapted for different muscle functions.

Introduction

Force and shortening in skeletal muscle are generated by cyclic interactions between the molecular motor myosin II and the actin filament, fuelled by ATP. Hydrolysis of each ATP provides ∼90 zJ of free energy (Pate & Cooke, 1989; Smith et al. 2005). During isometric contraction each attached myosin head exerts a force of about 6 pN while extending its own compliance by about 1.7 nm. During isotonic shortening against loads down to 0.5 times the isometric force, the 6 pN force can be wholly maintained in cyclically interacting myosin heads, while the filaments slide past each other by 5–7 nm (Piazzesi et al. 2007; Barclay et al. 2010). During this ‘working stroke’ the myosin head performs work amounting to as much as 40 zJ, which is about half the free energy from an ATP and much greater than the amount of work stored elastically in the attached myosin head at the start of the working stroke (Piazzesi et al. 2007).

All the above information is from studies of intact single muscle fibres from the frog (Linari et al. 1998; Piazzesi et al. 2002, 2003, 2007; Reconditi et al. 2004; Decostre et al. 2005). For isometric contraction, the force and the stiffness exerted by an attached myosin head can be determined from the macroscopic force and stiffness exerted by the muscle fibre and the filament lattice dimensions, if the fraction (n_ATT) of myosin heads attached to actin is known. Since the myosin heads act in parallel in the half-sarcomere, n_ATT can be calculated from the compliances of the half-sarcomere in isometric contraction and in rigor (where all myosin heads are attached to actin (Cooke & Franks, 1980; Lovell et al. 1981)) after subtracting the contribution of myofilament compliance. In Rana temporaria, n_ATT is 0.3 and the corresponding average force and stiffness of each attached myosin head are 5.3 pN and 3 pN nm⁻¹, respectively (Piazzesi et al. 2007); see Table 3.

Table 3.

Summary of observations on dogfish muscle and comparison with other species

		Dogfish S. canicula	Frog R. esculenta (thermody)	Frog R. esculenta (mechs)	Frog R. temporaria (mech/X-rays)	Rabbit skinned fibres no Dextran		Rabbit skinned fibres + 4% Dextran
A. Measurements normalised by CSA and quantities calculated from them
Isometric force	kPa	177 ± 13	1721	15523	2404	1905		2645
Filament compliance	nm/MPa	17.1 ± 1.0		12.5 ± 0.323	13.3 ± 0.44	21.0 ± 3.35		15.4 ± 1.25
Sarcomere compliance	nm/MPa	32.4 ± 1.6	23.31	25.123	20.44	43.05		26.45
Sarcomere compliance in rigor	nm/MPa	20.9 ± 0.6		15.42	15.44	28.25		18.65
Myosin head Strain	nm	2.27 ± 0.13	1.74 ± 0.251	1.76 ± 0.052	1.71 ± 0.144	4.03 ± 0.385		3.17 ± 0.285
z	nm	3.78 ± 0.22	2.90 ± 0.42			5.04
Compliance of attached Myosin heads in rigor	nm/MPa	3.8		2.9	2.1	7.2		3.2
B. Myosin head sites per CSA and measurements normalised by myosin head site
Myosin to myosin spacing	nm	43.3		41.0		48.86
Myofibrillar volume density	%	77.87		83		83*
Myosin head sites per CSA	μm−2	140,871		152,5128		119,800§		166,522§
Isometric force per Myosin head site	pN	1.26 ± 0.09	1.13	1.02	1.57	1.59		1.59
C. Proportion of myosin heads attached (nATT) and quantities dependent on proportion attached
Proportion attached from rigor observations		0.25 ± 0.08		0.23	0.30	0.335		0.295
Proportion attached from thermodynamic method		0.29 ± 0.04	0.221			0.315
Weighted mean of both methods		0.28 ± 0.04			0.30		0.32
Force per attached XB	pN	4.5 ± 0.66	5.14	4.43	5.29			5.48
Myosin head stiffness	pN nm−1	1.98 ± 0.31	2.95 ± 0.46	2.52 ± 0.45	3.09 ± 0.76			1.72 ± 0.26

Bold numbers are quantities calculated from the other entries in the Table. Dogfish and frog: 5oC. Rabbit: 12oC. Abbreviations: S, Scyliorhinus; R, Rana; thermody, thermodynamic; mech, mechanics.

¹(Decostre et al., 2005)

²(Fusi et al., 2010)

³(Brunello et al., 2009)

⁴(Piazzesi et al., 2007)

⁵(Linari et al., 2007)

⁶(Kawai et al., 1993)

⁷(Bone et al., 1986)

⁸(Barclay et al., 2010) (Appendix 1 and references therein)

^*as assumed for rabbit psoas muscle in (Linari et al., 2007)

^§Myosin head sites per CSA is given here in the absence of Dextran. Note that rabbit data from measurements made in Dextran is related to CSA measured without Dextran.

This same analysis of demembranated fibres from fast skeletal muscle of a mammal (see Table 3) revealed the stiffness of the myosin motor to be only ∼62% of the frog value (Linari et al. 2007). This raised the question of whether other mechanical (and thus the energetic) parameters of the molecular motor vary among animal species. To answer this question requires a wider range of the relevant mechanical and X-ray structural parameters than exist for mammalian muscle. Here we report a comprehensive series of experiments with structural and rapid mechanical methods on white muscle fibres isolated from dogfish. These fibres make up the bulk of the body and provide the propulsive power for fast swimming (Bone et al. 1986; Lou et al. 2002) and their mechanics and energetics properties relevant to swimming are known (Curtin & Woledge, 1991, 1993b, 1996; Curtin et al. 1997, 2010; Lou et al. 1997; West et al. 2004; Park-Holohan et al. 2010). Furthermore their striations are sufficiently uniform within single fibres to make them suitable for rapid mechanical experiments. The X-ray diffraction and rapid length perturbation (≤120 μs) results reported here are completely new, and are a pre-requisite for modelling the acto-myosin cycle of these fibres.

The results show: (i) the equivalent compliance of actin and myosin filaments is ∼17 nm MPa⁻¹, (ii) the fraction of attached myosin heads in isometric contraction (n_ATT) is 0.28, (iii) the average isometric force exerted by each attached myosin head is 4.5 pN, and (iv) the stiffness of the myosin head is 1.98 pN nm⁻¹. Thus, while most of the mechanical characteristics of dogfish myofilaments and myosin heads are similar to those of Rana temporaria, the stiffness of the myosin motor is less, only 71%. This result indicates that motor stiffness shows significant variation among animal species.

Methods

Ethical approval of the procedure for the specimen preparation

The experiments were carried out according to the guidelines laid down by our institutions’ animal welfare committees, and conform to the principles of UK regulations, as described in Drummond (2009). Experiments were done on white muscle fibres from dogfish (Scyliorhinus canicula, L). Fish were held at Imperial College London in tanks (1 m³) supplied with recirculating artificial seawater (12°C) and fed twice a week. The light–dark cycle was 12 h each. Fish were killed by a blow to the head and destruction of the spinal cord (ECC Directive 86/609 and according to Schedule I of the UK Animals (Scientific Procedures) Act 1986). Slices of white muscle were dissected from the tail musculature immediately posterior to the visceral cavity and transferred to ice-cold elasmobranch saline (mmol l⁻¹): NaCl, 292; KCl, 3.2; CaCl₂, 5.0; MgSO₄, 1.0; Na₂SO₄, 1.6; NaHCO₃, 5.9; urea, 483. Tubocurarine 1.5 mg l⁻¹ was included during dissection of the fibres. Saline without tubocurarine, referred to as ‘standard saline’, was used during all the experimental procedures, except where otherwise stated.

Mechanical experiments

Fibre bundles were transported to Florence in ice-cold saline. Single fibres (length: 3.7–5.3 mm; cross-sectional area (CSA): 0.013–0.050 mm²) were dissected and mounted in a thermo-regulated aluminium trough between the levers of a fast capacitance force transducer, resonant frequency 30–50 kHz (Huxley & Lombardi, 1980), and a servo-controlled loudspeaker motor (Lombardi & Piazzesi, 1990). The length change of a segment (0.75 to 1.6 mm long), selected in the one-third of the fibre near the force transducer end, was monitored by a striation follower with a time constant of 2 μs and a sensitivity of 100 mV nm⁻¹ per half-sarcomere (hs) (Huxley et al. 1981). It records the number of striations crossing each end of the selected fibre segment, thus generating two signals at each time point. The difference between these two signals estimates the average sarcomere length change in the segment (Lombardi & Piazzesi, 1990). Force, motor position and striation follower signals were recorded with an I/O board (PCI-6110E, National Instruments, Austin, TX, USA) and a LabVIEW (National Instruments) program.

Sarcomere length was set to 2.3 μm (at the right-hand end of the plateau of the isometric force–sarcomere length relation, see the online Supplemental Material). The CSA was calculated assuming elliptical area using width and height values measured at 0.5 mm intervals along the fibre. Tetanic stimulation, via platinum electrodes parallel to the fibre axis, consisted of alternate polarity pulses (0.5 ms duration) at a frequency giving a fused, or almost fused, force. Tetani were typically 0.35 s duration at 5°C and the interval between tetani was 4 min. Fibre compliance was measured by applying either step length changes, ΔL (complete in 110 μs, range −3 to +3 nm hs⁻¹) or 4 kHz sinusoidal ΔL (peak-to-peak ∼2.6 nm hs⁻¹). The length control system was used in fixed-end mode (the feedback signal was the position of the motor lever). To characterise the T₂ curve, step ΔL values between −15 and +3 nm hs⁻¹ were used.

To induce rigor the fibre was transferred to saline without urea and containing 20 mmol l⁻¹ BDM, and cooled to 1°C, then to urea-free BDM saline with metabolic inhibitors (mmol l⁻¹): iodoacetic acid, 1; 2,4-dinitrofluorobenzene, 5.6; sodium azide, 1 (Piazzesi et al. 2007; Fusi et al. 2010). Rigor induction was monitored by measuring fibre stiffness. Once in rigor, the fibre was rinsed with urea-free BDM saline, and returned to the standard saline. With this protocol fibre integrity and strong tendon attachments were maintained in all the seven fibres used. In four of the seven fibres, however, the sarcomere length signal from the striation follower became unreliable, probably because the signals from one end of the segment deteriorated (striations became irregular). In these cases the sarcomere compliance in rigor was calculated as described in Supplemental Material (see Fig. S2). In brief, rigor sarcomere compliance = rigor fibre compliance – tendon compliance, where tendon compliance = fibre compliance – sarcomere compliance, both measured during active contraction of the fibre before rigor. When this second method was applied to fibres that also provided a reliable sarcomere signal in rigor, the sarcomere compliance estimated with the two methods did not differ significantly (see Supplemental Material).

X-ray diffraction experiments

Experiments were done at the European Synchrotron Radiation Facility (ESRF, Grenoble, France) at beam line ID02 (up to 2 × 10¹³ photons s⁻¹ at 0.1 nm wavelength). Beam size at the fibre was ∼300 μm (horizontal, full width at half-maximum, FWHM) and ∼100 μm (vertical). Fibre bundles were transported to ESRF in ice-cold saline and bundles of two fibres were dissected just before the experiments. The bundle was mounted, via aluminium foil clips on the tendons, on the hooks of the motor and force transducer. Two mica windows were located close to the fibres, about 600 μm apart, to minimise the X-ray path in solution. Fibre dimensions were determined as described above. The trough was mounted vertically at the beam line. The beam was attenuated for fibre alignment. To minimise radiation damage, an electromagnetic shutter (nmLaser Products, Inc., Sunnyvale, CA, USA) limited X-ray exposure to the data collection periods, and the fibre bundle was moved vertically by 0.2 mm between tetani. Data were collected from 20–40 tetani in each fibre bundle with no detectable sign of radiation damage. X-ray diffraction patterns were recorded using the FReLoN CCD-based detector with an image intensifier (Narayanan et al. 2001) and active area 100 × 100 mm²; the detector was mounted 2.3 m from the fibre bundle. The 2048 × 2048 pixels of the CCD were binned by 8 in the horizontal direction and 2 in the vertical direction before the readout to increase signal-to-noise ratio. The point spread function of the FReLoN detector was ∼250 μm (FWHM), and the combined instrumental point spread function was negligible compared with the radial width of the M3 reflection. X-ray data are presented from three fibre bundles with cross-sectional area 0.044 ± 0.004 mm² (SEM) and isometric plateau force (T₀) 172 ± 14 kPa (SEM).

Experimental protocol

Fibre bundles (5°C, SL ∼2.3 μm) were tetanically stimulated every 4 min at 18–25 Hz. At 200 ms after the stimulus start, when force had attained the isometric plateau (T₀), a ramp length change was imposed. Shortening (velocity 0.66 ± 0.01 μm s⁻¹ hs⁻¹ (SEM)) decreased force to ∼0.5 T₀ and lengthening (velocity 0.177 ± 0.001 μm s⁻¹ hs⁻¹ (SEM)) increased force to ∼1.8 T₀. X-ray diffraction frames (5 ms exposure) were collected at rest, at the isometric tetanus plateau force, and during the steady force produced by shortening or lengthening.

X-ray data analysis

Fit2D (A. Hammersley, ESRF) and IgorPro (WaveMetrics, Inc., Lake Oswego, OR, USA) software were used. Two-dimensional patterns were centred and aligned using the equatorial 1,1 reflections, then mirrored horizontally and vertically. The quasi-helical repeat of the crowns of the myosin heads along the thick filament generates a series of reflections based on a 43 nm periodicity on the meridional axis (parallel to the fibre axis). The intensity distribution along the meridional axis was calculated by integrating from 0.012 nm⁻¹ on either side of the meridian. To estimate the changes in the extension of the myosin filament, the spacing of the 6th order myosin-based reflection at ∼7.2 nm (M6) was used, instead of the more intense 3rd order reflection at ∼14.5 nm (M3), because M6 reflection is specifically related to a periodic structure on the thick filament backbone and, due to the relatively large conformational dispersion of the myosin heads, is less sensitive than the M3 reflection to the influence of actin-attached myosin heads (Huxley et al. 2003; Reconditi et al. 2004; Huxley et al. 2006). The 6th and 7th order actin layer lines (AL6 and AL7), which are generated by the double stranded helical arrangement of the actin monomers, were used to estimate the changes in the extension of the actin filament. The distribution of intensities around AL6 and AL7 was integrated in the region between 0.034 and 0.059 nm⁻¹ from the meridional axis. The equatorial intensity distribution was determined by integrating from 0.0036 nm⁻¹ on either side of the equatorial axis. The spacing of the equatorial 1,1 reflection, originating from the lattice planes formed by the myosin filaments, was used to estimate the distance between myosin filaments. Background intensity distributions were fitted using a convex hull algorithm or straight-line fitting and subtracted. The patterns from frog muscle fibres at rest (collected during the same visits to ESRF) were used to calibrate the spacings of the reflections, assuming that the spacing of M3 was 14.34 nm (Haselgrove, 1975).

Statistics

Values reported are given as means ± standard error of the mean, except where otherwise stated.

Results

X-ray diffraction experiments

In low angle X-ray diffraction patterns from bundles of dogfish fibres at rest (Fig. 1A, left), the quasi-helical arrangement of the myosin heads along the thick filament is responsible for the myosin layer lines. ML1, the most intense, corresponds to the 43 nm periodicity (Huxley & Brown, 1967). At a larger distance from the centre, two less intense layer line reflections, AL6 and AL7, corresponding to 5.9 and 5.1 nm spacings, are due to the thin filament helical periodicity. On the meridional axis regularly spaced reflections correspond to higher orders (2nd to 8th) of the 43 nm spacing. The most intense, M3, is due to the 14.5 nm axial repeat of myosin heads. Along the equatorial axis the pattern contains reflections arising from the double hexagonal lattice of thick and thin filaments, indexed according to the planes of this lattice as 1,0, 1,1, etc.

Figure 1. X-ray diffraction.

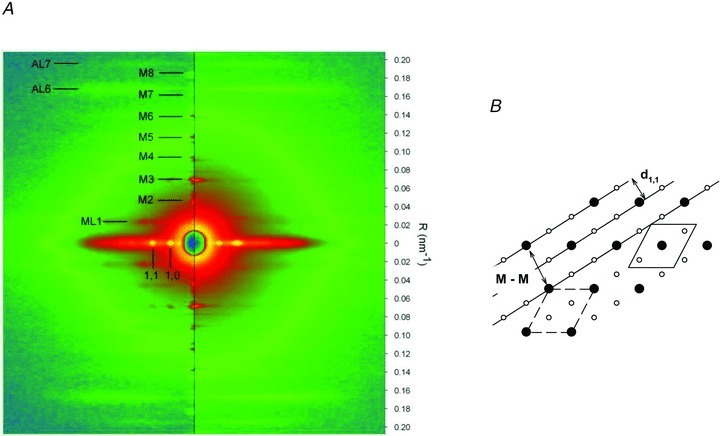
A, two-dimensional diffraction patterns from dogfish muscle fibres at rest (left half) and at tetanus plateau (right half). The vertical axis (meridional) is parallel to the fibre axis and the scale on the right indicates the position in reciprocal space (nm⁻¹). The myosin-based meridional reflections are indexed as M1 … M8. ML1, AL6 and AL7 indicate the first myosin-based layer line and the actin-based layer lines. The horizontal (equatorial) axis (perpendicular to the fibre axis) contains the (1,0) and (1,1) reflections. The two patterns are the sum of 5 ms frames from 3 fibre bundles, for a total exposure time of 105 ms at rest and 140 ms at the plateau of the isometric tetanus. B, diagram of the hexagonal array of thick and thin filaments in the myofilament lattice. The distance d_1,1 between the continuous lines (representing the 1,1 planes) is half the myosin-to-myosin spacing (M-M). The unit cell, containing one thick filament, is shown by the dashed line. The shifted version of it, continuous line, makes more explicit the ratio 1:2 between myosin and actin filaments.

At the plateau of an isometric tetanus (Fig. 1A, right), M3 and to a lesser extent M6 remain strong, while the other meridional reflections become very weak. M3 broadens and moves closer to the centre of the pattern (see also Fig. 2B), indicating an increase in the axial periodicities by about 1.4% (as in frog muscle; Huxley et al. 1982; Linari et al. 2000). M6 changes similarly.

Figure 2. Values from X-ray diffraction.

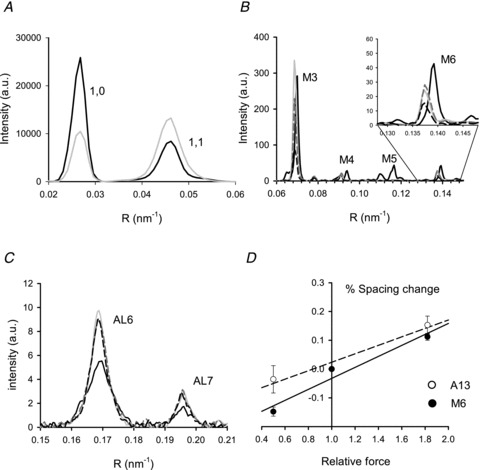
A, intensity profiles of the equatorial reflections 1,0 and 1,1 at rest (black line) and at T₀ (grey line). B, intensity profiles of the myosin meridional reflections from M3 to M6. Black and grey lines as in A; grey dashed line during shortening and black dashed line during lengthening. The inset shows the region around the M6 on an expanded scale. C, intensity profiles of the 6th and 7th actin layer lines. Line code as in B. D, percentage change in spacing of M6 (•) and A13 (○, calculated as explained in the text) versus force. The slopes of the linear regression fits to M6 data (continuous line) and to A13 data (dashed line) estimate myosin and actin filament compliance, as described in the text and Table 1. Total exposure times: 50 ms rest, 25 ms tetanus.

At rest the equatorial 1,1 reflection (corresponding to lattice planes that include the thin and the thick filaments, see Fig. 1B) is weaker than the 1,0 reflection (corresponding to the lattice planes that include only the thick filaments). During a tetanus the 1,1 reflection broadens and becomes brighter than the 1,0 (Fig. 2A) due to the movement of the myosin heads towards the thin filaments to bind actin (Haselgrove & Huxley, 1973). The spacing of the 1,1 reflection at rest is used to estimate the distance between thick filaments, a parameter used for calculating the force of an individual myosin head. The spacing between thick filaments (M-M in Fig. 1B) is 43.31 ± 0.09 nm (three fibre bundles) and is twice the spacing of the 1,1 reflection (d_1,1 in Fig. 1B). The unit cell in Fig. 1B contains one myosin filament and the length of each side is 43.3 nm, and thus unit cell area = sin(60 deg) × 43.3²= 1624 nm². The density of filaments within the myofibril cross section is thus 616 filaments μm⁻². Myofibrils occupy 77.8% of the volume of dogfish white muscle fibres (Bone et al. 1986), so the density of filaments in the whole fibre cross section is 0.778 × 616 = 479 filaments μm⁻². There are 147 myosin molecules, each with two heads, in each half thick filament. Thus with all myosin heads attached, the number of myosin heads acting in parallel in the half-sarcomere would be 2 × 147 × 479 = 140,871 heads μm⁻². In the Discussion this value will be used to calculate the force exerted by an individual myosin head.

X-ray diffraction measurements of the compliance of the thick and thin filaments

The compliances of the filaments have been determined from the changes in spacings of the M6 (SM6), AL6 (SAL6) and AL7 (SAL7) reflections during shortening (V=∼0.7 μm s⁻¹ hs⁻¹, T=∼0.5 T₀) and during lengthening (V=∼0.2 μm s⁻¹ hs⁻¹, T=∼1.8 T₀). Figure 2B shows the intensity profiles of M3 to the M6. The thick filament compliance was estimated from the change in SM6, which is specifically related to periodic structures in the thick filament backbone. The actin filament compliance could not be measured directly from the change in spacing of the meridional reflection A13 (SA13), originating from the 2.7 nm axial repeat of actin monomers, since it is too weak in the pattern from single fibres or bundles of a few fibres. The actin filament compliance was estimated from the changes of SAL6 and SAL7, which are due to a combination of a change in the filament extension and also its twisting/untwisting. Figure 2C shows the intensity profiles of AL6 and AL7. The value SA13 was calculated using the relation 1/SA13 = 1/SAL6 + 1/SAL7 (Squire, 1981).

Figure 2D shows how SM6 and SA13 vary with force. The slopes of the two relations represent the change in length of the thick filament (S_M) and thin filament (S_A) for a force change of T₀. S_M is 0.19 ± 0.04%T₀⁻¹ and S_A is 0.15 ± 0.03%T₀⁻¹. The corresponding thick and thin filament compliances are shown in Table 1. The total filament compliance (C_f=C_M+C_A) = 15.1 ± 2.4 nm MPa⁻¹.

Table 1.

Filament compliance from X-ray experiments

	Mean ± SEM		Mean ± SEM	units
SM	0.19 ± 0.04	SA	0.15 ± 0.03	%T0−1
cM	3.80 ± 0.80 (1)	cA	2.23 ± 0.45 (2)	nm μm−1T0−1
	22.1 ± 4.7 (5)		13.0 ± 2.6 (5)	nm μm−1 MPa−1
CM	1.27 ± 0.27 (3)	CA	1.34 ± 0.27 (4)	nm T0−1
	7.36 ± 1.66 (5)		7.77 ± 1.68 (5)	nm MPa−1

Means and standard error of mean for 3 fibre bundles. Slope from Fig. 2D, S; compliance, C and c. Subscripts: M, myosin filament; A, actin filament. (1) c_M=S_M×ζ/(ζ/2) =S_M× 2, (2) c_A=S_A×l_A/(l_A−ζ/2) (Ford et al. 1981; Linari et al. 1998), (3) C_M=c_M× (l_M− 2/3 ×ζ), and (4) C_A=c_A× (l_A− 2/3 ×ζ), where ζ is the length thick and thin filament overlap in a hs = 700 nm, l_M is myosin filament length in a hs = 800 nm, and l_A is actin filament length in a hs = 1065 nm (for sarcomere length of 2.3 μm and a bare zone width of 170 nm). (5) for T₀= 172 ± 14 kPa (average for X-ray experiments, n= 3).

Mechanical experiments: fibre and half-sarcomere compliance at the plateau of isometric tetanus

Figure 3A shows a sample record of the force, the half-sarcomere length change, and the fibre length change during the step protocol in a tetanic contraction. During the rise of tetanic force, the sarcomeres in the selected segment shorten by 20 nm per half-sarcomere (hs), as they extend the tendon and stretch weaker regions along the fibre, outside the segment. Four length steps were imposed at 200 ms intervals; two releases and two stretches were each followed after 50 ms by a return step to optimize the repriming of the original isometric condition. The force changes during these steps are superimposed and shown on an expanded time scale in Fig. 3B. The relationship between the force attained at the end of the step and the size of the step, T₁ relation (Huxley & Simmons, 1971), is shown in Fig. 3C for the fibre (filled circles) and for the hs (open circles). The abscissa intercepts are the elastic strain of the fibre and of the half-sarcomere at the force preceding the step, T₀ (Table 2A). The difference between these values is the contribution of the tendon to the fibre compliance. The tendon compliance is 23% the total fibre compliance and is similar to that in frog fibres (Cecchi et al. 1987). The slope of the hs regression line (Table 2B) measures the hs stiffness, e, and its reciprocal is the half-sarcomere compliance, C_hs. The mean value of half-sarcomere compliance in six fibres with T₀ of 166 ± 8 kPa was 32.4 ± 1.6 nm MPa⁻¹.

Figure 3. Fibre and half-sarcomere compliance at the plateau of isometric contraction.

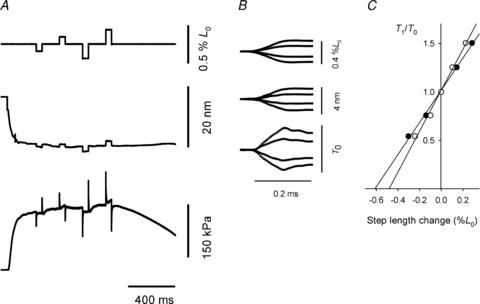
A, isometric force development and force response to four length steps of different sizes at 200 ms intervals. Each step is followed, after 50 ms, by a step in the opposite direction. From top to bottom traces are fibre length change, hs length change and force. Fibre length 5.01 mm; CSA 0.032 mm²; 5°C. B, sections of the records at the time of the steps, superimposed and on an expanded time scale. C, T₁ relations for the fibre (•) and for the half-sarcomere (○) obtained from the records in B.

Table 2.

Values from step length experiments at plateau of isometric tetanus

A. Elasticity from length steps.
	Fibre	Half-sarcomere	Tendon	Units
Elastic strain	0.61	0.47	0.14a	%L0−1

B. Half-sarcomere stiffness and compliance from step length changes.
hs stiffness, e		2.11 ± 0.11		%L0−1
		0.184 ± 0.010b		T0 nm−1
hs compliance, Chs		5.44 ± 0.28		nm T0−1
Example in Fig. 3		32.2c		nm MPa−1
Mean, 6 fibres		32.4 ± 1.6d		nm MPa−1

^atendon strain = fibre strain half-sarcomere strain, all at T₀.

^bfor half-sarcomere length = 1.15 μm

^cfor T₀= 169 kPa for fibre in Fig. 3

^dfor T₀= 166 ± 8 kPa, for 6 fibres.

Half-sarcomere compliance during development of tetanic force

Stiffness during the development of force in an isometric contraction was measured by imposing 4 kHz length oscillations (peak-to-peak 0.23%L₀, starting from 0.2 T₀; Fig. 4A). As force rises, the amplitude of the sine wave component of the force record increases, indicating an increase in hs stiffness. Stiffness was also measured by imposing small length steps at different times during force development. Half-sarcomere strain (S_hs) was calculated as force/half-sarcomere stiffness. During tetanus rise, the relationship between S_hs and force is linear and similar for step length changes and length oscillations (Fig. 4B, slope = 17.5 ± 1.1 nm MPa⁻¹, intercept = 2.27 ± 0.13 nm). As for hs compliance (see above), the hs strain is the sum of the contributions from three elastic elements: the myosin filament, the actin filament and the array of attached myosin heads (Ford et al. 1981; Linari et al. 1998). Assuming that, as previously found in frog fibres (Brunello et al. 2006; Fusi et al. 2010), the force development is due to a proportional increase in the number of attached myosin heads, the linear increase in hs strain with force is due to the increase in myofilament strain. Thus in Fig. 4B the slope measures filament compliance (C_f= 17.5 ± 1.1 nm MPa⁻¹) and the intercept is the average strain of the array of the attached myosin heads (S_x= 2.27 ± 0.13 nm). The C_f value measured in this way is not significantly different from the independent estimate obtained in the X-ray experiments (C_f= 15.1 ± 2.4 nm MPa⁻¹). The mean of the two estimates of C_f, weighted inversely by their variances, is 17.1 ± 1.0 nm MPa⁻¹ (Table 3). This value of C_f is used to calculate the compliance of the myosin head array and the fraction of myosin heads attached.

Figure 4. Strain and compliance during the tetanus rise and at different forces in rigor.

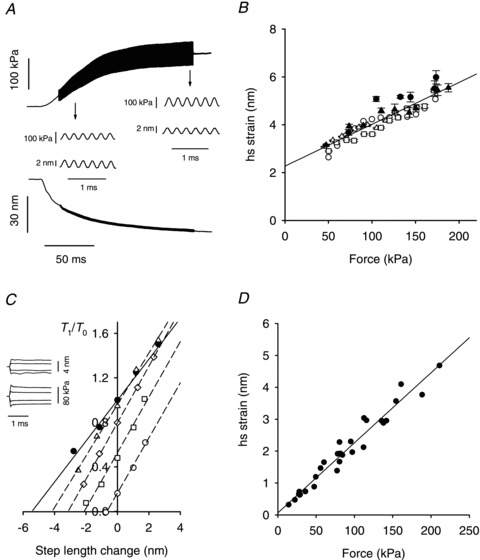
A, force and half-sarcomere length traces showing the superimposed 4 kHz oscillations during the isometric force development. The insets: force and hs length oscillations on an expanded time scale at the times indicated by the arrows. Fibre length, 5.25 mm; CSA, 0.023 mm²; segment length, 1.29 mm. B, relation between half-sarcomere strain (S_hs) and force (T) during tetanus rise, from length steps (filled symbols) or 4 kHz oscillations (open symbols). Pooled data from six experiments (different symbols). The median of 5 observations per step group and 47 per oscillation group. Line: linear regression of pooled data, S_hs=C_f×T+S_x, where C_f, the filament compliance = 17.5 ± 1.1 nm MPa⁻¹ and S_x, the myosin head strain = 2.27 ± 0.13 nm. C, T₁ relations in active contraction (•, from open circles in Fig. 3C) and in rigor (open symbols) at four different steady forces (▵, 0.95 T₀; ◊, 0.8 T₀; □, 0.5 T₀; ○ 0.2 T₀). The slopes (hs stiffness, T₀ nm⁻¹) of the linear regressions are 0.184 ± 0.009 (•), 0.231 ± 0.007 (▵), 0.254 ± 0.003 (◊), 0.249 ± 0.009 (□), 0.247 ± 0.001 (○). D, half-sarcomere strain versus steady force from three fibres in rigor. Force has been normalised by the CSA in the relaxed fibres.

Half-sarcomere compliance in rigor

The half-sarcomere compliance in rigor was determined by superimposing length steps on different levels of steady force, T, attained at the end of slow stretches (duration 2 s, amplitude 2–10 nm hs⁻¹). In Fig. 4C the extreme force reached at the end of the step (called T₁ by analogy with the response to a step in active contraction; Fig. 3B) is plotted versus the step size for different force values in rigor (open symbols). For comparison, T₁ in active contraction (filled circles) is also shown. The slope of the T₁ relation in rigor, hs stiffness (e_R=∼0.25 T₀ nm⁻¹) is independent of the steady force T and is 33% larger than in the active contraction. Consequently, the strain of the half-sarcomere in rigor (S_hs,R=T/e_R) increases in proportion to T as shown in Fig. 4D. The slope of the linear regression is 22.0 ± 0.9 nm MPa⁻¹ (=C_hs,R); the intercept, 0.06 ± 0.09 nm is not significantly different from zero. In four of the seven fibres used for these measurements, the sarcomere length changes could not be reliably measured in rigor. In these cases the hs compliance in rigor was calculated by subtracting the tendon compliance from the fibre compliance, as explained in Methods (see Supplemental Material for more details). The mean value of the hs compliance in rigor (C_hs,R) was obtained using a single value for each fibre. For three fibres it was the average of the results from the two methods. For the other four fibres it was the value from the method shown in Supplemental Material. The mean value, 20.9 ± 0.6 nm MPa⁻¹ (n = 7), represents the half-sarcomere compliance when all myosin heads are attached. The compliance of the array of myosin heads in rigor, C_x,R, was obtained by subtracting C_f, the myofilament compliance from C_hs,R. Thus C_x,R is 20.9 −17.1 = 3.8 ± 1.2 nm MPa⁻¹.

Effect of temperature on half-sarcomere compliance during contraction

We used length steps and 4 kHz oscillation protocols to investigate how hs compliance in active contraction is affected by temperature (0–20°C). Figure 5A shows that between 5 and 20°C hs compliance, C_hs, is constant; mean = 32.2 ± 0.7 nm MPa⁻¹ (22 measurements, 8 fibres). Thus, as for frog fibres (Piazzesi et al. 2003; Decostre et al. 2005), the number of attached myosin heads remains constant and force change with temperature is due to a change in force per attached myosin head (see next section). The compliance of the myosin head array in contraction is found by subtracting filament compliance from half-sarcomere compliance, C_x=C_hs−C_f= 32.2 − 17.1 = 15.1 ± 1.2 nm MPa⁻¹.

Figure 5. Effect of temperature on the half-sarcomere compliance and on the isometric force.

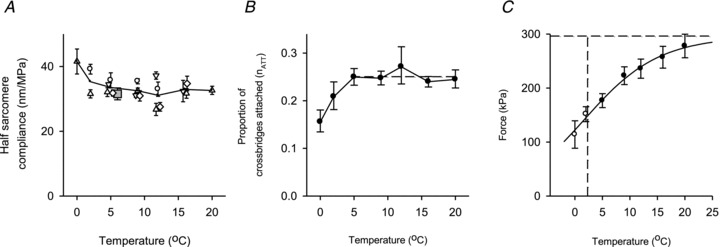
A, half-sarcomere compliance versus temperature from four experiments identified by different open symbols. The compliance was measured using 4 kHz oscillations (○) or length steps (other open symbols). To avoid overlap some points are shifted slightly along the temperature axis. Each point is the mean of 3–50 steps (median 11), or for oscillations the mean from 3 to 6 contractions each with >200 measurements. Line and ▴: mean result of all four experiments. Grey square; mean from four other experiments at 5°C only. B, temperature dependence of proportion of attached myosin heads (n_ATT) estimated from the average values of C_hs in A (see text). Broken line: mean 5–20°C. C, relationship between force and temperature in the range 5–20°C (•) and <5°C (○). Data are the means from five experiments using the method described in Supplemental Material. Continuous line: text eqn (1) fitted to (•). Horizontal dashed line: 296 kPa. Vertical dashed line: 2.3°C, where Q= 1 and T_θ= 0.5 × (n_ATT×T_A).

The fraction of myosin heads attached in isometric contraction, n_ATT, can be obtained from the following relationship, n_ATT=C_x,R/C_x. Figure 5B shows that between 5 and 20°C n_ATT is constant, mean = 0.25 ± 0.08. At less than 5°C the hs compliance was larger than at higher temperatures (Fig. 5A), as found for fibres from the frog Rana esculenta at temperatures less than 2°C (Piazzesi et al. 2003; Decostre et al. 2005). At extremely low temperature n_ATT may decrease due to a smaller Ca²⁺ transient produced by electrical stimulation.

Effect of temperature on isometric force

The amount of isometric force developed by an active fibre at different temperatures was determined using force records like that shown in Fig. 3A. Temperature affects the rate of force development, such that the time required to develop the steady isometric force (T₀) increases as the temperature is reduced. Thus the time interval between the start of stimulation and the first length step was adjusted to take account of much of this effect. Residual variation in the extent of force development at the first length step was taken account of by the method shown in Supplemental Material. The relationship between force and temperature after taking account of this effect is shown in Fig. 5C.

As described previously (Piazzesi et al. 2003; Decostre et al. 2005; Woledge et al. 2009) the temperature (θ in K) affects force (T) by changing the equilibrium constant (Q) for the transition between the first two states (A1 and A2) of the attached myosin heads.

where ΔH and ΔS are the enthalpy and entropy changes of the reaction and k_b is Boltzmann's constant. If the A1 state produces no force, then the force T_θ at temperature θ (K) is:

1

where T_A is the force that would be exerted if all attached myosin heads were in the A2 state and n_ATT is the fraction of myosin heads attached. This equation was fitted to the filled circles in Fig. 5C with ΔH, ΔS and (n_ATT×T_A) as free parameters. The value of (n_ATT×T_A) is 296 ± 20 kPa (horizontal dashed line) and ΔH is 160 ± 36 zJ molecule⁻¹. The open circles in Fig. 5C were omitted from the fitting because, as discussed above, the value of n_ATT is reduced at temperatures below 5°C.

Force recovery after length steps

The elastic response elicited by a length step imposed on an isometrically contracting fibre (Fig. 3) is followed by a partial recovery, within a few milliseconds, to a force T₂. The recovery is due to the synchronous execution of the working stroke by the myosin heads attached before the length step (Huxley & Simmons, 1971). This phase is followed by a pause or inflection in force recovery and then by a slower recovery to the original isometric force due to detachment–reattachment of myosin heads (Huxley & Simmons, 1971; Piazzesi et al. 1992). Figure 6A shows sample records of force and hs length during and after length steps of various amplitudes. A clear inflection between the quick and slower phases of force recovery was rare in the experiments reported here, likely due to the fact that sarcomere length control was not used. Consequently the rate of quick recovery is slowed by shortening against tendon compliance, and the size of this effect increases with the release amplitude as can be seen in the hs length records. Therefore T₂ was estimated as shown in Fig. 6A. Force recovers in a single phase after a step stretch, but was not taken as the T₂ value, as it has been demonstrated that in such cases detachment–reattachment of myosin heads merges with the reversal of the working stroke (Piazzesi et al. 1997).

Figure 6. Relationship between quick force recovery and step size.

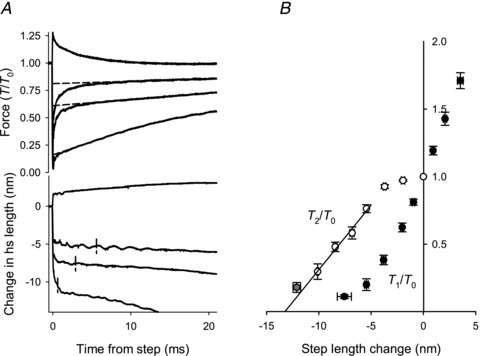
A, example records of force (upper panel) and of hs length change (lower panel) during and after step length changes. The force attained in the quick recovery (T₂) was measured by back-extrapolating the later phase of force recovery to the time of the step, as shown by the broken lines. The value of T₂/T₀ is the ordinate intercept of the broken lines. Vertical lines in the lower panel mark hs length change and the time at which force had recovered to T₂/T₀. B, T₁/T₀ (•) and T₂/T₀ (○) versus hs length change. Data from four experiments, grouped in classes of hs length changes of 1.5 nm hs⁻¹ except the grey circle for which the range is 10.5–14 nm hs⁻¹. The bars show the SEM values in both X and Y directions where these are larger than the size of the symbols. The full line is the regression line through T₂/T₀ points for steps larger than 5 nm. Abscissa intercept =−13.8 ± 0.4 nm.

T₁ and T₂ values in Fig. 6B were obtained by averaging data from individual fibres after grouping as described in the figure legend. T₂ is close to T₀ for length steps smaller than 5 nm, and for larger releases T₂ decreases linearly with step size (Huxley & Simmons, 1971; Ford et al. 1977). The linear fit to the T₂ points intersects the length axis at −13.8 ± 0.4 nm. A release of this size fully abolishes the ability of the working stroke to regenerate force and also takes up the filament compliance previously extended by the isometric force (187 ± 10 kPa in this group of observations). The amount of hs shortening accounted for by the filament compliance is 0.0171 nm kPa⁻¹× 187 kPa = 3.2 ± 0.2 nm, so the maximum filament sliding attributable to the myosin heads during rapid force recovery is 13.8 − 3.2 = 10.6 ± 0.4 nm.

Discussion

We report here a complete set of experimental measurements on dogfish fibres from which the properties of the myosin heads and filaments can be evaluated (Table 3). Insight into the mechanism of energy transduction can be obtained by considering these properties and how they compare with those of muscles from other animals. This discussion assumes that the work performed by a muscle during shortening is due to the mechanical properties of the array of myosin heads and is broadly based on the Huxley–Simmons model (Huxley & Simmons, 1971). A key feature is that the myosin head can maintain force, in spite of the removal of work from it as it moves to drive filament sliding, because it is continually recharged during its working stroke and because ‘exhausted’ myosin heads are replaced by new ones.

Comparison of the mechanical characteristics in different species

How do the mechanical and energetic parameters of the filaments and myosin heads of fast-twitch muscle fibres of different animal species compare? Previously reported values (Table 3) show that the stiffness of the myosin head in rabbit (Linari et al. 2007) is only 62% of the value in frog (best estimate, 2.78 ± 0.30 pN nm⁻¹, of values in Table 3 weighted by 1/variance). However, because this is a comparison of intact fibres (frog) with demembranated fibres (rabbit), other factors, such as the loss of soluble proteins or irreversible lattice expansion following membrane permeabilisation, might influence the mechanical properties and appear as a reduction in myosin head stiffness. For this reason the dogfish results for intact fibres are quite important in allowing a straightforward comparison of the properties of intact fibres from another animal, frog.

The total equivalent filament compliance in dogfish muscle, 17.1 ± 1.0 nm MPa⁻¹, is greater than that of frog, 13.0 ± 0.4 nm MPa⁻¹ (best estimate of values in Table 3 weighted by 1/variance). This difference is 4.1 ± 1.1 nm MPa⁻¹. The fact that dogfish actin filaments (l_A, 1.065 μm) are longer than those of frog (0.95 μm) contributes to this difference. The compliance added by the ‘extra’ length of the thin filament (Δl_A) in dogfish is

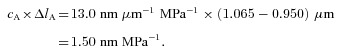This value is less than the difference between the total equivalent filament compliance of dogfish and frog, 4.1 ± 1.1 nm MPa⁻¹. What other factors might be involved? The value of c_A (compliance per unit length of actin filament) as measured by X-ray diffraction of dogfish, 13 ± 3 nm μm⁻¹ MPa⁻¹ is greater than that for frog, 10 ± 2 nm μm⁻¹ MPa⁻¹ (Linari et al. 1998). These dogfish vs. frog values of c_A are not significantly different at the 5% level. However, the difference between the mean values is sufficient to produce extra total equivalent filament compliance in dogfish of 1.7 nm MPa⁻¹, which together with that due to the difference in thin filament length, provides a plausible explanation for most of the larger total equivalent filament compliance in dogfish. It seems unlikely that the myosin filament properties contribute to the larger total equivalent filament compliance in dogfish because the measured values of c_M are similar, 22 ± 5 nm μm⁻¹ MPa⁻¹ for dogfish and 23 ± 1 nm μm⁻¹ MPa⁻¹ for frog (Reconditi et al. 2004).

We calculate z, the length change in the myosin head responsible for the isometric force assuming that force is generated in the transition from the non-force generating state, A1, to the first force generating state, A2 (Decostre et al. 2005). As illustrated in Fig. 7A, the value of z is 3.78 ± 0.22 nm. As shown in Table 3, the value for frog is smaller, 2.90 ± 0.42 nm. The proportion of attached myosin heads, n_ATT, can be estimated by the slope (0.29 ± 0.04) of the relationship shown in Fig. 7B, and is based on the assumption that the free energy change (ΔG) of the force generating transition, A1 to A2, is the maximum work each attached myosin head can do (Huxley & Simmons, 1971; Woledge et al. 2009). The abscissa values (expressed in zJ per attached myosin head) show the increase in ΔG with temperature above 2.3°C (θ= 275 K); values are calculated from the ΔH of the A1 to A2 transition. The ordinate values show the increase in the maximum work that a myosin head transition can do (zJ per myosin head); values are calculated as the product of z and the change in isometric force with temperature above 2.3°C (θ= 275 K). The value of n_ATT from Fig. 7B, 0.29 ± 0.04, agrees with the value, 0.25 ± 0.08, obtained from the comparison of stiffness of myosin heads during active contraction with that in rigor. In the rest of this discussion we will use 0.28 ± 0.04 for n_ATT, which is the average of the two estimates where the contribution of each is weighted by the factor 1/variance of the estimate. As shown in Table 3, the dogfish value is within the range, 0.22 to 0.31, reported for frog.

Figure 7. Myosin head properties and implications for the acto-myosin cycle.

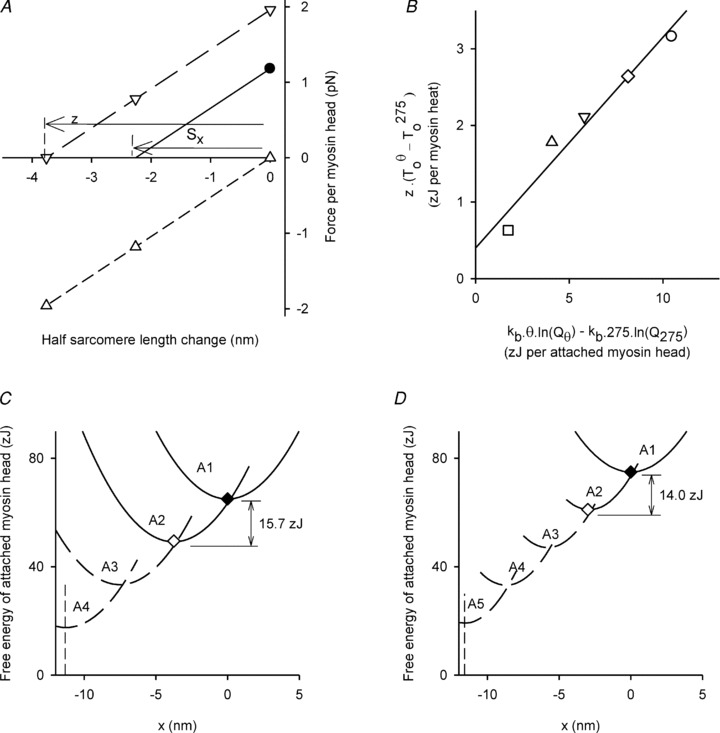
A, dogfish: the measured isometric force per myosin head is shown as •. The full line shows how the force varies with a rapid length change. The intercept (S_x) is the strain in the myosin head before length change. The dashed lines show forces with all myosin heads: in the A2 state (▿, long dashes), or in the A1 state (▵, short dashes). All three lines are parallel because both states have equal stiffness. The observed proportion of heads in the A2 state at 5°C is 0.60 (Fig. 5C). Thus with all the heads in the A2 state, the length change required to reduce force to zero, z, is 3.78 nm (=S_x/0.6). B, dogfish: effect of temperature on two different estimates of the maximum work in the transition from state A1 to state A2. Each point is for a different temperature and shows the extra work above that at 2.3°C: □ 5°C, ▵ 9°C, ▿ 12°C, ◊ 16°C and ○ 20°C. The abscissa values (units: zJ per attached myosin head) are calculated from temperature and the corresponding equilibrium constant (Q, see Fig. 5C), and k_b (Boltzmann's constant). The ordinate values (units: zJ per myosin head) are calculated from the values of z and the observed force (T₀) at each temperature. The slope of the regression line (n_ATT= attached myosin heads/total myosin heads) is 0.29 ± 0.04. For a more detailed discussion of this method of finding n_ATT see Woledge et al. (2009). C, dogfish: full lines: x dependence of free energy of the A1 and A2 states with ◆ and ◊ marking the free energy minima. x: displacement from the length at which the force in state A1 is zero. The free energy curves are positioned vertically so that the proportion of A2 at equilibrium is 0.60 (at x= 0). The energy charge to the myosin head is the difference between the minima. Broken lines show the free energy profile of two further hypothetical states A3 and A4 and the broken vertical line marks the shortest length at which force could be exerted by these states (see text). D, frog: as C except that there are three further hypothetical states.

Our results show that the force exerted per myosin head is 1.26 pN (5°C, Table 3B, = 177 kPa/140,871 myosin heads μm⁻²). The force per attached myosin head, 4.5 ± 0.66 pN, is the force per myosin head divided by the fraction attached, n_ATT (= 1.26 ± 0.09 pN/0.28 ± 0.04). The corresponding values for frog range from 4.4 to 5.3 pN and are thus very similar to the dogfish value.

The stiffness of the attached head in dogfish, 1.98 ± 0.31 pN nm⁻¹, is force per attached head divided by strain (= 4.5 pN/2.27 nm). This is only 71% of that in frog (2.78 pN nm⁻¹). The difference is due to the lower value of myosin head strain in frog (1.74 nm) than dogfish (2.27 nm). The P value for the difference in myosin head stiffness is between 0.05 and 0.10. The conventional value for statistical significance, P < 0.05, was not reached, but the relatively low P value indicates that the stiffness values are more likely to be different than the same. On the basis of present knowledge we conclude that, among the parameter reported here, stiffness of the attached head exhibits the largest variation between fast skeletal muscles of different species; this parameter also varies between fibre types (Seebohm et al. 2009). Such a difference in myosin head stiffness has important consequences in models of the acto-myosin cycle (see below and also Offer & Ranatunga (2010)).

Energy transduction and myosin head stiffness

Curtin & Woledge (1993b) observed that 41% of the enthalpy used by dogfish white muscle fibres during sinusoidal movement was produced as work. Probably about 15% of the enthalpy in these contractions would have been used by the sarcoplasmic reticulum for calcium pumping (Lou et al. 1997; West et al. 2004) and so the work produced was 48% of the enthalpy used by the myosin heads (= 41/(100–15)). The enthalpy would have come predominantly from phospho-creatine splitting at 56 zJ/molecule. The average work done by each myosin head cycle in dogfish white muscle performing sinusoidal movement is therefore about (0.48 × 56 =) 27 zJ per myosin head cycle. How does this value compare with the energy charge received by the myosin head in the A1 to A2 transition?Figure 7C illustrates the free energy of the A1 and A2 states and their dependence on x (the displacement of the myosin heads from the position at which the force in state A1 is zero). These curves have been calculated from the measurements of myosin head stiffness, z and the equilibrium distribution of A1 and A2 obtained from the temperature dependence of force. The difference between the minimum free energy of A1 and the minimum free energy of A2, 15.7 zJ, is the energy charge for this transition. This recharge energy is clearly less than the work per myosin head cycle, 27 zJ, so additional recharging is required. Another line of evidence for additional recharging comes from the T₂ results. A length change of 10.6 nm is required to exhaust the capacity of the myosin head to exert force; this value is much greater than z, 3.78 nm. As shown in Fig. 7C (broken lines), following the Huxley and Simmons model (1971), two further transitions each similar to the A1 to A2 transition are necessary to explain the recharging that accounts for the working stroke completion. On this hypothesis the total work per myosin head cycle is 47 zJ, sufficient to account for the observed work, and the total distance over which force can be exerted is 11.3 nm which is consistent with the T₂ results. In Fig. 7D the corresponding properties of frog muscle are shown. The energy change in the A1 to A2 transition for frog is 14.0 zJ, somewhat less than that for dogfish. If we again assume further transitions, each similar to the A1 to A2 transition, then three such transitions are required to account for the T₂ results (Lombardi et al. 1992; Linari et al. 2009) corrected for filament compliance (Barclay et al. 2010). For further discussion of the working stroke see Decostre et al. (2005) and Piazzesi et al. (2007).

Summary

We have found that the compliance of the sarcomere in single fibres from fast-twitch dogfish muscle is larger than that in frog fibres, in part because of the longer thin filament. The force generated by the myosin head in isometric contraction is similar, while the stiffness of the attached myosin head is smaller in dogfish than in frog. These two facts mean that the elastic strain in the attached myosin head in isometric contraction is greater in dogfish than frog and that the dogfish myosin head requires less recharging than frog to complete the 11 nm working stroke. There is evidence about myosin head stiffness varying between fibre types (Seebohm et al. 2009) and the efficiency of energy transduction also varies between fibre types (Curtin & Woledge, 1993a,b; Barclay & Weber, 2004). How the properties of, for example, slow-twitch fibres compare among species remains to be investigated.

Glossary

Abbreviations

A1-A4

force-generating states of attached myosin head

AL6

6^th order actin-based X-ray layer line

AL7

7^th order actin-based X-ray layer line

BDM

2,3-butanedione monoxime

CSA

cross-sectional area

ESRF

European Synchrotron Radiation Facility

FWHM

full width at half maximum

hs

half-sarcomere

M3

3^rd order myosin-based meridional X-ray reflection

M6

6^th order myosin-based meridional X-ray reflection

ML1

1^st order myosin-based X-ray layer line

SAL6

spacing of AL6 X-ray reflection

SAL7

spacing of AL7 X-ray reflection

SL

sarcomere length

SM6

spacing of M6 X-ray reflection

Author contributions

The experiments were performed at the European Synchrotron Radiation Facility, Grenoble, France (X-ray), and the Laboratory of Physiology, Department of Evolutionary Biology, University of Florence (fibre mechanics) using tissue prepared at the Molecular Medicine Section, National Heart and Lung Institute, Imperial College London, London, UK. The following authors participated in performing the experiments, data collection and drafting the article: S.P.-H., M.L., M.R., L.F., E.B., M.I., M.D., V.L., T.G.W. and G.P. The following authors contributed to the conception and design of the experiments, analysis and interpretation of data, drafting the article or revising it critically for important intellectual content: M.L., M.I., V.L., N.A.C., R.C.W. and G.P. All authors approved the final version of the manuscript.