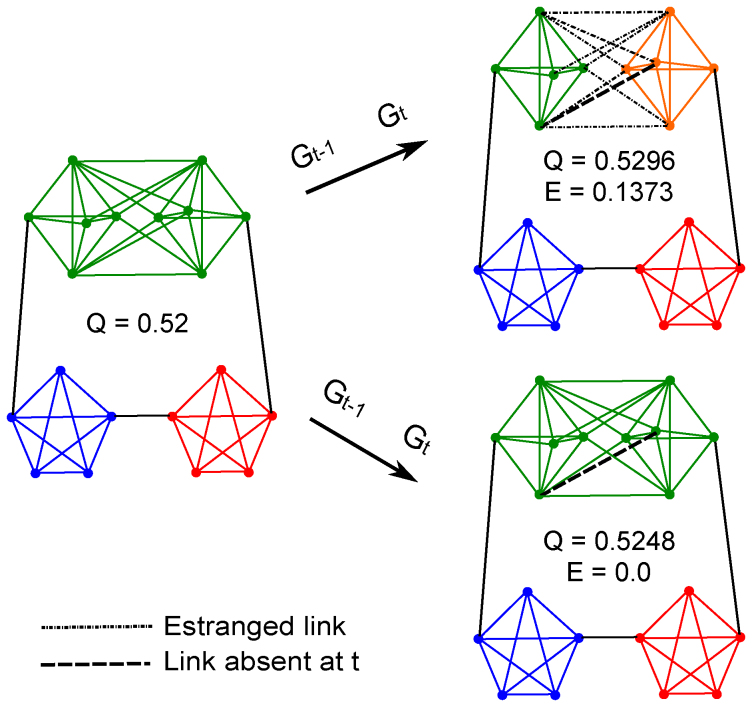
Figure 1. An example illustrating the detection of temporal communities via estrangement confinement.

The network on the left, G_t–1 consists of 20 nodes and 52 links, and a maximal modularity partition of this network consists of three communities represented by the three colors (Q = 0.52). In the next snapshot, the network has evolved to G_t which differs from G_t–1 only in the absence of a single link, indicated by the dotted line. The top right and bottom right networks both represent the same network G_t, but indicate distinct choices of community partitions available. The partition shown on the top right, 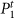consists of 4 communities, and is the partition that gives the highest modularity . The partition 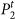for G_t shown on the bottom right which preserves the node partition chosen for G_t–1 has a slightly lower modularity of 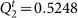. The partition 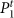with higher modularity, however, makes 7 links estranged. The estranged links (shown in gray) are those intra-community links at t – 1 that change to inter-community links at t. Notice that links in the orange community of 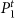despite having changed their community affiliation from t – 1 to t are not estranged since they are still intra-community links. In contrast to 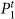, the partition 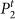yields no estranged links. Estrangement, E, defined as the fraction of estranged links at t is therefore 0 for 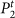but 7/51 = 0.13 for 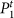. Maximizing modularity while constraining estrangement to a low value (e.g. 0.05) therefore yields 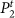as the partition for G_t, yielding a smoother temporal progression of the community structure from t – 1 to t.