Figure 2. Mapping community labels from time t – 1 to time t.

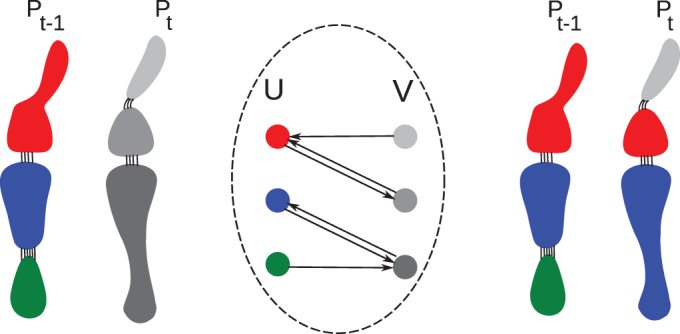
The left panel shows the situation after estrangement confinement has found a partition of the graph at time t, consisting of three communities. Two of these have arisen due to an uneven split of the red community at t – 1, and one due to the merging of the blue and green communities at time t – 1. The mapping procedure causes fewest nodes to change labels from t – 1 to t. The center panel shows the bipartite construction that the mapping procedure uses. Here, nodes on the left (set U) represent communities at t – 1 and nodes on the right (set V) represent those at time t. Each node in U has an outgoing link to the node in V with whom its Jaccard overlap is maximal. Similarly each node in V has an outgoing link to the node in U with whom its Jaccard overlap is maximal. For simplicity, we say that each node points to its maximal overlap partner in the other set. Once these links are drawn, the mapping procedure allows inheritance of labels only between pairs of nodes which have bidirectional links between them, i.e., a node in U (community at t – 1) passes on its label to a node in V (community at t) only if they are maximal overlap partners of each other. Conseqeuntly, a node in U which is not bidirectionally connected to any node in V, does not pass on its label (e.g., the green node in U). Similarly, a node in V which is not bidirectionally connected to any node in U, does not inherit a label, and therefore obtains a new label (e.g., the topmost node in V). The progression of appropriately labeled communities from t – 1 to t after the mapping step is shown in the panel on the right.