Penalization of aperture complexity in inversely planned volumetric modulated arc therapy

Abstract

Purpose: Apertures obtained during volumetric modulated arc therapy (VMAT) planning can be small and irregular, resulting in dosimetric inaccuracies during delivery. Our purpose is to develop and integrate an aperture-regularization objective function into the optimization process for VMAT, and to quantify the impact of using this objective function on dose delivery accuracy and optimized dose distributions.

Methods: An aperture-based metric (“edge penalty”) was developed that penalizes complex aperture shapes based on the ratio of MLC side edge length and aperture area. To assess the utility of the metric, VMAT plans were created for example paraspinal, brain, and liver SBRT cases with and without incorporating the edge penalty in the cost function. To investigate the dose calculation accuracy, Gafchromic EBT2 film was used to measure the 15 highest weighted apertures individually and as a composite from each of two paraspinal plans: one with and one without the edge penalty applied. Films were analyzed using a triple-channel nonuniformity correction and measurements were compared directly to calculations.

Results: Apertures generated with the edge penalty were larger, more regularly shaped and required up to 30% fewer monitor units than those created without the edge penalty. Dose volume histogram analysis showed that the changes in doses to targets, organs at risk, and normal tissues were negligible. Edge penalty apertures that were measured with film for the paraspinal plan showed a notable decrease in the number of pixels disagreeing with calculation by more than 10%. For a 5% dose passing criterion, the number of pixels passing in the composite dose distributions for the non-edge penalty and edge penalty plans were 52% and 96%, respectively. Employing gamma with 3% dose/1 mm distance criteria resulted in a 79.5% (without penalty)/95.4% (with penalty) pass rate for the two plans. Gradient compensation of 3%/1 mm resulted in 83.3%/96.2% pass rates.

Conclusions: The use of the edge penalty during optimization has the potential to markedly improve dose delivery accuracy for VMAT plans while still maintaining high quality optimized dose distributions. The penalty regularizes aperture shape and improves delivery efficiency.

INTRODUCTION

Volumetric modulated arc therapy (VMAT) is fast becoming a popular form of radiation therapy for its ability to produce highly conformal treatment plans, often with shorter treatment times and with fewer monitor units (MUs) than conventional fixed-gantry intensity-modulated radiation therapy.¹ Potential advantages of the shorter treatment time enabled by VMAT include reduced patient motion during treatment, increased patient comfort, an improvement of patient flow due to shorter treatments, and reduced leakage through MLC leaves compared to IMRT plans. VMAT is currently being explored and implemented for a variety of treatment sites including prostate, spine, brain, head and neck, lung, and cranio-spinal treatments.^{2, 3, 4, 5, 6, 7}

During the optimization of VMAT plans, individual control point apertures are usually optimized by iteratively adjusting the position of MLC leaves and recalculating the optimization objectives to check for plan improvement (referred to as direct aperture optimization or DAO).⁸ Aperture weights can also be optimized simultaneously. A disadvantage associated with this kind of inverse optimization is that the generated apertures have the potential to be irregularly shaped with small leaf gaps and spatially separated areas. It is difficult for dose calculation algorithms to accurately predict the dose for these apertures because of the lack of charged particle equilibrium, requiring very precise modeling of lateral electron scatter.⁹ The effect of complex apertures on accurate dose delivery becomes magnified for treatment sites that contain small target volumes and/or nearby normal tissue structures. While it is likely that Monte Carlo dose calculation algorithms are better suited to handle calculations for complex plans, the accuracy of the calculation is not the sole motivation for limiting aperture complexity. A higher degree of complexity in VMAT apertures also leads to a greater dependence on the accuracy of MLC leaf positioning¹⁰ as well as the accuracy of the MLC modeling in the treatment planning system. Increasing plan complexity can increase the number of monitor units needed to deliver a plan by a sizable amount, and leads to a greater susceptibility to motion and interplay effects. Constraints on the minimum aperture area and minimum leaf gap help to avoid unreasonably complex apertures, however, even with these constraints, the creation of complex apertures with an unacceptable amount of uncertainty in the dose calculation remains a consequence of inverse planning.

A number of studies have shown that an increased degree of complexity in VMAT plans and individual apertures leads to reduced dosimetric accuracy.^{11, 12, 13} Fog et al. showed that dose calculations for small apertures with a width of 0.5 cm in some cases underestimated the maximum dose in the field by over 20% and the width of the penumbra by over 100%.¹³ Measurement devices with coarse resolution [existing 2D array detectors typically have a resolution of greater than 7 mm (Ref. ¹⁴)] or analysis with too large distance to agreement criteria can mask these dose calculation errors for irregularly shaped individual apertures and heavily modulated composite dose distributions. As VMAT becomes an increasingly popular treatment option, it is important that we understand the errors in dose calculations for given aperture shapes such that we ensure calculated dose distributions can be accurately delivered as planned.

One way to prevent optimized VMAT plans from including apertures that are known to be associated with unacceptable error in the dose calculation is to include aperture shape-related feedback in the DAO process. In this paper, we investigate the use of an aperture-regularization objective function integrated into the optimization process. We refer to this new metric as the “edge metric.” A penalty based on this metric can reduce unnecessary complexity in the optimized plan by driving the optimizer toward a solution with smoother aperture shapes with larger areas and thus reduced dosimetric uncertainty. The penalty works similarly to cost function-sensitive smoothing in IMRT, in that unnecessary complexity in the plan can be removed without degrading the resulting plan quality.^{15, 16} We compare VMAT plans created with and without our aperture-regularization objective function to assess its performance and investigate dose calculation accuracy using radiochromic film.

METHODS AND MATERIALS

Development and implementation of an aperture-based cost function

To promote more regularly shaped apertures, minimum leaf gap and minimum aperture area constraints are often implemented in DAO schemes. However, a minimum leaf gap cannot prevent highly modulated fields with very narrow or noncontiguous regions from being generated during the optimization. Here, we will evaluate whether there is a correlation between the measured error in the dose calculation and the area of the aperture, and investigate whether a stronger correlation can be found using the proposed edge metric.

By analyzing the distribution of errors in calculated doses for aperture shapes generated without using an aperture-based penalty, we have found that the majority of the error is concentrated on the edges of the apertures defined by the MLC leaves. This is expected in most dose calculation algorithms as even a small mismatch in the penumbra width can cause large deviations on the edge of the dose distribution, particularly for small apertures. This deviation between calculated and delivered dose at the field edges can be exacerbated by the tongue and groove effect of the MLC leaves.

As a result, we have developed a metric that quantifies the amount of “edge” in the aperture. Our metric is defined as

$$M=\sum _{i=1}^N{W}_i\times \frac{C_1{x}_i+C_2{y}_i}{A_i},$$ (1)

where x and y are the lengths of the aperture perimeter defined by the MLC leaf ends and sides, respectively. Figure 1 shows a graphical representation of these parameters. The constants C₁ and C₂ are scaling factors to adjust the relative importance of the x and y edges individually, A is the aperture area, and W is the aperture weight. The sum is over all apertures indicated by the index i. The penalty based on this metric is simply the metric multiplied by a global scaling factor, C,

$$P=C\sum _{i=1}^N{W}_i\times \frac{C_1{x}_i+C_2{y}_i}{A_i}.$$ (2)

To include the edge penalty in the direct aperture optimization process, the penalty is recalculated after each optimization iteration and added to the dose-related cost function penalty to determine the total cost function penalty. The value of C in Eq. 2 is chosen at the beginning of the optimization and defines the importance of the edge penalty relative to that of the dose-related cost function. C is fixed throughout the entire optimization of the plan; however, note that as the optimization progresses, the ratio of the edge penalty to the total cost function value will change. All edge penalty weights in this paper are expressed as a percentage of the total cost function value. This is done because the numerical value of C has little relevance on its own, since all institutions will use different dose-related cost functions and initial plan setup for their VMAT plans. Additionally, the reported edge penalty weights are the weights after optimization of the plan is complete. This notation was chosen because the initial weight of the penalty before optimization can depend strongly on the initial plan design (such as the trajectory of each arc and the initial aperture shapes).

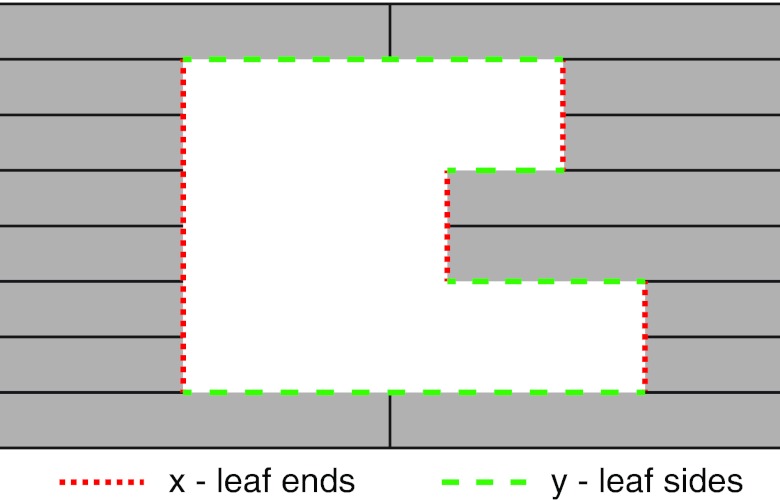
Figure 1.

Example aperture illustrating the parameters x and y in Eqs. 1, 2. The parameter x corresponds to the MLC leaf ends (vertical dotted lines) and y corresponds to the MLC leaf sides (horizontal dashed lines).

The ratio of the aperture perimeter to the aperture area has been used previously as an aperture complexity measure,¹⁷ although to our knowledge it has never been used within an optimization cost function. Additionally, the edge penalty has important features that improve its performance compared to simply calculating the perimeter-area ratio. The separation of the leaf ends and sides into two individually weighted quantities allows the user to tailor the penalty depending on where dose calculation errors are observed for individual apertures. We have found the strongest correlation between measured dosimetric error (i.e., the number of pixels in a measurement film differing from calculation by more than a set threshold) when the constant C₁ is set to zero and only the MLC leaf sides are considered in the penalty. This can be explained by examining Fig. 1, where one can see that the only way to affect the value of the C₁x term in Eq. 2 is to close or open leaf pairs. The number of open leaf pairs does not necessarily correlate well with aperture irregularity, and therefore may not improve the performance of the penalty. All of the results in this paper use Eq. 2 with C₁ = 0 and C₂ = 1. However, the general form of the penalty shown in Eq. 2 allows the user to customize the penalty.

Another important feature of the edge penalty as shown in Eq. 2 is the inclusion of the aperture weight, W_i. If the penalty does not include the weight, the optimization is biased to the regularization of apertures with the lowest number of monitor units, since changing these apertures will have the least dosimetric impact. This is the opposite of the desired effect, since the apertures that contribute most to dose discrepancies between the calculated and delivered doses will be the least affected by the penalty.

Planning and dose calculation

Treatment planning for VMAT plans was done using University of Michigan's in-house treatment planning system, UMPlan, with an improved version of the Edge/Octree dose calculation model.^{18, 19} In UMPlan, each gantry position is defined as a control point. For each patient, control point beams were equally spaced at 4° intervals. As described for each case below, gantry angles were sometimes removed for angles where critical normal tissues were located in front of the target (e.g., some of the anterior beams were removed for the paraspinal case). The initial aperture shape for each beam was shaped to the PTV with a 5 mm margin. The jaws were shaped to the PTV with a 1.5 cm margin in the direction parallel to leaf motion and a 0.5 cm margin in the direction perpendicular in leaf motion. This allowed ample space for the MLC leaf positions to be optimized, but prevented the optimization system from spuriously opening leaf pairs outside of the target area (only leaf pairs within the jaw openings were allowed to move). Jaw positions remained fixed throughout the optimization. The details of the optimization system can be found in Ref. 20 which discusses a unique inverse planning method referred to as inverse-optimized 3D conformal planning. For initial testing, we created a new plan for a paraspinal SBRT case that was previously treated in our clinic. This treatment site is ideal because treatment volumes are often only a few centimeters in diameter, and this type of target is likely to cause small, irregular apertures to be generated during optimization.

The chosen patient had a PTV wrapped one third of the way around the spinal cord at the level of T7. The volume of the PTV was 15.9 cc, and the prescription dose for the PTV was 36 Gy in 12 Gy fractions. Additionally, a GTV was drawn within the PTV and prescribed to 40 Gy. Planning objectives are summarized in Table 1 and were designed based on clinical practice at our institution.

Table 1.

Planning objectives for the example paraspinal SBRT case. The prescription for this case was 36 Gy in 12 Gy fractions to the PTV.

Priority	Structure	Goal
1	Cord	Max dose < 24 Gy
2	PTV	Min dose > 36 Gy
	GTV	Min dose > 40 Gy
3	Esophagus	Max dose < 27 Gy
	Aorta	Max dose < 30 Gy
	Lung	V20 < 10%
	All other normal tissue	ALARA

Each plan that was created had a total of 61 control points equally spaced posteriorly between 60° and 300° (some of the anterior beams were manually removed to reduce dose to normal tissues). Normal tissue “rings” around the PTV were defined to help the optimizer step down the dose and reduce hotspots outside of the target. The first ring of high dose normal tissue (HDNT) began 1 mm outside of the PTV and extended out to 1.5 cm. The second ring (HDNT2) was defined from 1.6 to 3 cm, and the third (LDNT) included all remaining normal tissue covered by the radiation arc. Points in contoured normal tissue structures were excluded from the normal tissue rings.

A plan was first optimized using only physical machine constraints on aperture shape. We then experimented with the scaling of our edge penalty function [parameter C in Eq. 2] and analyzed the effect of the penalty on the end cost function value and resultant apertures. All other objectives and initial conditions for the optimizations were identical between plans.

After initial testing, the effect of the edge penalty on aperture complexity and plan quality was also tested on a brain SBRT case with a PTV slightly overlapping the brainstem, and a liver SBRT case where the lesion abutted the duodenum. The brain case had two arcs, one from 181° to 293° and another from 347° to 115° with a total of 62 beams each separated by 4° (two arcs were used because some beam angles were manually removed before optimization in order to avoid critical structures). The liver case had one 360° arc with 92 beams. Planning goals for these two cases are shown in Tables 2, 3. The same general planning strategies as used for the paraspinal case were used for both the brain and the liver cases.

Table 2.

Planning objectives for the example brain SBRT case. The prescription for this case was 25 Gy in 5 Gy fractions to the PTV.

Priority	Structure	Goal
1	Brainstem	No more than 10% > 20 Gy
2	PTV	Min dose > 25 Gy
3	All other normal tissue	ALARA

Table 3.

Planning objectives for the example liver SBRT case. The prescription for this case was 50 Gy in 10 Gy fractions to the PTV.

Priority	Structure	Goal
1	Small bowel	Max dose < 30 Gy
	Stomach	Max dose < 27.5 Gy
	Cord	Max dose < 25 Gy
2	PTV	Min dose > 50 Gy
3	All other normal tissue	ALARA

For comparison of plans with and without the edge penalty added to the optimization, we used a variety of evaluation criteria. Dose volume histogram (DVH) analysis as well as minimum dose to 95% of the target (D95), conformality index (CI), maximum dose to 0.1 cc of organs at risk (OARs), and mean doses were used to compare target coverage and doses to normal tissues. The CI was defined as the volume of the reference isodose (V_RI) divided by the target volume (TV).²¹ Plan complexity was evaluated in terms of the edge penalty metric [Eq. 1], the total number of plan MUs, as well as visual inspection of the optimized aperture shapes.

Dosimetric validation of the edge penalty

To quantitatively measure the effect of the edge penalty on accuracy in our dose calculation, Gafchromic EBT2 film (ISP, Wayne, NJ) was used to measure dose distributions for beam apertures generated with and without the edge penalty applied in the optimization process. For this type of experiment, dosimetric measurements using film are advantageous because of their high degree of spatial resolution. Additionally, radiochromic film has the advantages of being self-developing and nearly tissue equivalent.

Dose distributions for individual VMAT beam apertures were recalculated on a simple, 30 cm cubic solid water phantom with gantry and collimator angles set to zero. Composite dose distributions were also generated on the solid water phantom using the original gantry and collimator angles. Only static apertures were calculated and measured in order to isolate errors in the dose calculation from errors due to interpolation between VMAT control points. Dose distributions were calculated on a 1 mm grid.

The 15 highest weighted beam apertures from each of two paraspinal plans with and without the edge penalty were chosen for measurement. The plan with the penalty turned on had a penalty weight of 3.1% of the total cost function after optimization was complete. This plan was chosen because the optimized apertures were observably more regularly shaped compared to the plan without the edge penalty, while plan quality was not considerably altered (see Sec. 3A). Individual beam apertures were measured on 10 × 8.5 cm pieces of EBT2 film. The film was irradiated at a depth of 10 cm with 20 cm of backscatter. Each film was centered on central axis before irradiation. The MUs delivered for each aperture were scaled such that the maximum dose in the field was approximately 2 Gy. Additionally, 25.4 × 20.3 cm pieces of film were used to measure a composite of all 15 apertures in each group in the coronal plane. The composite measurements used the original beam angles and optimized MUs, scaled to again deliver a maximum dose in the field of 2 Gy. Lastly, to create a sensitometric curve, a calibration film set was irradiated with doses from 0 to 3 Gy using a sheet of EBT2 film cut into 12 equal pieces.

An Expression 10000XL scanner (Epson, Long Beach, CA) with all color correction turned off was used to scan the film at a resolution of 96 dpi. A film template slightly smaller than the irradiated films was aligned with the scanning axis and affixed to the scanner bed to ensure that the same central area of the scanner bed was used for each measurement. The template also prevented contact between the film and the scanner bed which can lead to ring artifacts. The film was marked to ensure that every measurement was made with the same film orientation. Film measurements for all apertures were completed using a single film batch. Conversion of measured optical density to dose was performed using the triple-channel nonuniformity correction described by Micke et al.²² in order to reduce the effects of film nonuniformity and any scanner artifacts. The nonuniformity correction was implemented in MATLAB (Mathworks, Natick, MA).

Via the same MATLAB program, measured dose distributions were registered in Fourier-space to calculated dose distributions to maximize agreement between the two. Because the films were aligned to central axis during irradiation and then aligned to the scanning template, only small adjustments (<1 mm, <1° ) were necessary. Only doses of at least 10% of the maximum measured dose in the aperture were considered for dose comparison between measured and calculated doses. We define the percent dose deviation for a single pixel as the local dose difference (calculated – measured) normalized by the maximum calculated dose in the field.

For error analysis of measured versus calculated composite doses, we performed both a gamma analysis²³ and gradient compensation,²⁴ individually. We used a range of distance-to-agreement (DTA) criteria from 1 to 3 mm, and a dose difference of 3%. For analyzing individual beam apertures, we performed a direct comparison between the measured and calculated doses. For quantitative analysis of the dose calculation accuracy for the apertures, we determined the percentage of pixels with a deviation of greater than 10%.

RESULTS

Effect of edge penalty on plan quality

To test the effects of adding the edge penalty during optimization, the penalty was added at varying weights from zero to about 50% of the total cost function value after optimization for three different body sites: paraspinal, brain, and liver. Plans were compared using DVH analysis and various metrics for the target and normal tissue structures, as well as conformality and total plan MUs.

For all of the results shown in this paper, the constant C₁ from Eq. 2 was set to zero and C₂ was set to unity. These values were chosen based on observed correlations between the calculated edge penalty and measured dose calculation errors (see Sec. 3C). The only remaining free parameter to determine was then an appropriate global scaling factor, C, of the edge penalty.

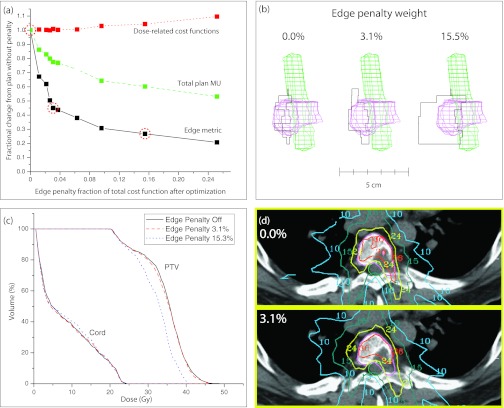
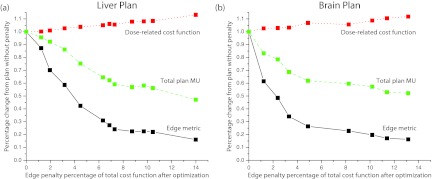
To determine the optimal edge penalty scaling factor, we plotted the dose-related cost function penalty, plan MUs, and the edge metric as a function of the edge penalty weight (i.e., the ratio of the edge penalty to the total cost function value after optimization was complete). The edge metric serves as a measure of aperture complexity, and is defined in Eq. 1. In Fig. 2a, the dotted line shows the dose-related cost function penalty (the total cost function not including the edge penalty), the dashed line shows the total plan MUs, and the solid line shows the edge metric. The y-axis is scaled so that the plotted values are relative to the results when the edge penalty is turned off. As expected, as the edge penalty weight is increased, the general trend is for the dose-related cost function penalty to increase and the plan MUs and edge metric to decrease. For an edge penalty weight of about 3.1%, the dose-related cost function penalty is increased by 1% compared to the plan without the penalty, and the edge metric is decreased by 55% compared to the plan without the penalty. Additionally, the MUs for this plan were reduced by 22% compared to the plan without the penalty. For a penalty weight of about 2.5%–6%, the edge metric can be dramatically reduced while only having a minor effect on the dose-related cost function value. Above this weight, a further reduction in the edge metric comes at the cost of a noticeable reduction in plan quality. Figure 2b illustrates how the aperture shape of a single beam changes as the penalty weight is increased from 0% to 15.3%. The contours of the PTV and cord are also shown. Figure 2c shows the DVH's for the PTV and cord for the plans with a penalty weight of 0%, 3.1%, and 15.3%. Lastly, Fig. 2d shows an example slice for plans with a penalty weight of 0% (top slice) and 3.1% (bottom slice) with isodose lines for 36, 24, 15, and 10 Gy. These results illustrate how the plan changes only slightly when the edge penalty is added at the low weight of 3.1%. However, as the weight of the penalty increases, plan quality can be affected, as shown in the DVH curve for the PTV for the plan with a penalty weight of 15.3%. At this point, the optimizer places too much emphasis on creating large, regularly shaped apertures, and compromises on other planning goals to achieve this goal.

Figure 2.

(a) Effect of increasing the weight of the edge penalty on the dose-related cost function penalty, total plan MUs, and the edge metric. The dotted line shows the value of the dose-related cost function, the dashed line shows the total plan MUs, and the solid line shows the edge metric (i.e., the aperture complexity). (b) Example aperture shapes from three different plans with penalty weights of 0%, 3.1%, and 15.3% of the total cost function after optimization [these points are circled in part (a)]. The contours of the cord and PTV are shown. (c) DVHs for the cord and PTV for three example plans with penalty weights of 0%, 3.1%, and 15.3% of the total cost function after optimization. (d) Example slices showing the 36, 24, 15, and 10 Gy isodose lines for a plan without the edge penalty (top) and a plan with a penalty weight of 3.1% (bottom). Contours of the PTV and cord are shown.

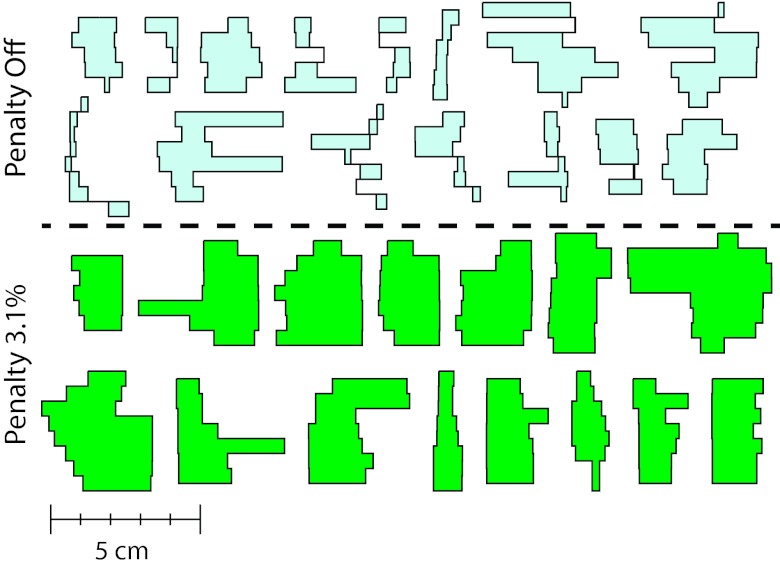
To better illustrate the effect of the edge penalty on the aperture shapes, Fig. 3 shows apertures generated without an edge penalty (top set) and with an edge penalty with a weight of 3.1% (bottom set). In this figure, the 15 highest weighted apertures for each plan are shown. These are the same apertures that were used for the film measurements described in Sec. 3C. The apertures generated with the penalty are larger and less complex compared to those generated without the penalty. Additionally, all apertures with spatially separated regions have been eliminated.

Figure 3.

Fifteen highest weighted apertures from the paraspinal VMAT plans without (top set) and with (bottom set) an edge penalty with a weight of 3.1% of the total cost function value after optimization.

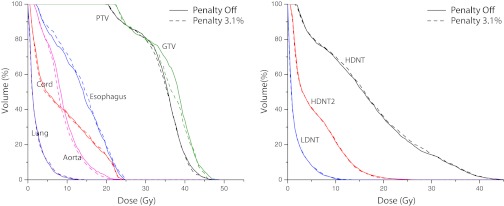
Figure 4 shows a comparison between the DVHs for the plans with the apertures shown in Fig. 3. The target structures as well as relevant OARs are included. At a weight of 3.1%, the edge penalty has a minor effect on the DVH curves. The mean dose to the esophagus is slightly increased and the mean dose to the aorta is slightly decreased when the penalty is turned on. The dose to the PTV is also nearly the same while some loss of coverage to the GTV is observed. Dose to normal tissue rings defined around the PTV are shown in the right graph in Fig. 4. All of the normal tissue rings have essentially identical DVH results. This result illustrates the fact that the larger apertures are primarily irradiating more of the PTV per gantry angle, instead of irradiating more normal tissue. Table 4 shows some relevant metrics for comparison between the two plans (max values are to 0.1 cc). CI decreases very slightly from 0.61 to 0.59 when the penalty is turned on, while the MUs are reduced by 22.5%.

Figure 4.

Comparison of DVH curves for target tissues (left graph) and OARs (right graph) for the paraspinal VMAT plans without (solid lines) and with (dotted lines) an edge penalty with a weight of 3.1%.

Table 4.

Target and normal tissue metrics for the paraspinal penalty off and on (3.1% weight) plans. Maximum doses are to 0.1 cc.

	Cord	PTV	GTV	Esophagus	Aorta	Conformality
	Max/mean	D95/mean	D95/mean	Max/mean	Max/mean	index	MUs
	(Gy)	(Gy)	(Gy)	(Gy)	(Gy)	(VRI/TV)	(norm)
Penalty off	21.8/8.3	23.6/35.4	24.5/36.6	22.9/13.4	20.8/9.0	0.61	100
Penalty 3.1%	21.9/8.2	23.4/35.1	24.3/35.8	23.3/14.2	20.4/8.6	0.59	77.5

Additional clinical examples

To further investigate the edge penalty under different treatment geometries, we also used one SBRT brain and one SBRT liver case. Figure 5 shows how the edge metric and dose-related cost change as the edge penalty weight is increased for the two studied cases. Tables 5, 6 show some relevant metrics comparing plans without and with the edge penalty for these two body sites. For comparison purposes, the penalty weight for the plans in the tables was chosen as close as possible to the weight that was used for the paraspinal plan that was measured with film (3.1%). The liver plan had a weight of 3.2% and the brain plan had a weight of 3.3%. Because there were fewer nearby OARs for the particular cases chosen, we have also included the normal tissue rings around the target to show how the dose drops off outside of the PTV (these rings are defined in Sec. 2B).

Figure 5.

Effect of increasing the edge penalty weight on the dose-related cost function penalty, total plan MUs, and the edge metric for the SBRT liver case (left) and the SBRT brain case (right).

Table 5.

Target and normal tissue metrics for the liver penalty off and on (3.2% weight) plans. Maximum doses are to 0.1 cc.

	Duodenum	PTV	HDNT	HDNT2	LDNT	Conformality
	Vol > 30 Gy/mean	D95/mean	Max/mean	Max/mean	Max/mean	index	MUs
	(cc/Gy)	(Gy)	(Gy)	(Gy)	(Gy)	(VRI/TV)	(norm)
Penalty off	0.81/4.5	41.0/58.8	52.0/24.6	39.5/10.1	29.5/2.9	1.09	100
Penalty 3.2%	0.78/4.3	40.6/59.2	53.0/25.5	36.5/10.4	28.5/3.0	1.11	86.2

Table 6.

Target and normal tissue metrics for the brain penalty off and on (3.3% weight) plans. Maximum doses are to 0.1 cc.

	Brainstem	PTV	HDNT	HDNT2	LDNT	Conformality
	D10/mean	D95/mean	Max/mean	Max/mean	Max/mean	index	MUs
	(Gy)	(Gy)	(Gy)	(Gy)	(Gy)	(VRI/TV)	(norm)
Penalty off	18.7/9.3	20.0/26.6	24.5/12.3	16.5/7.0	14.5/3.2	0.92	100
Penalty 3.3%	18.9/9.0	20.0/25.8	23.0/12.8	15.5/7.0	11.5/3.1	0.99	68.7

Dosimetric validation of the edge penalty

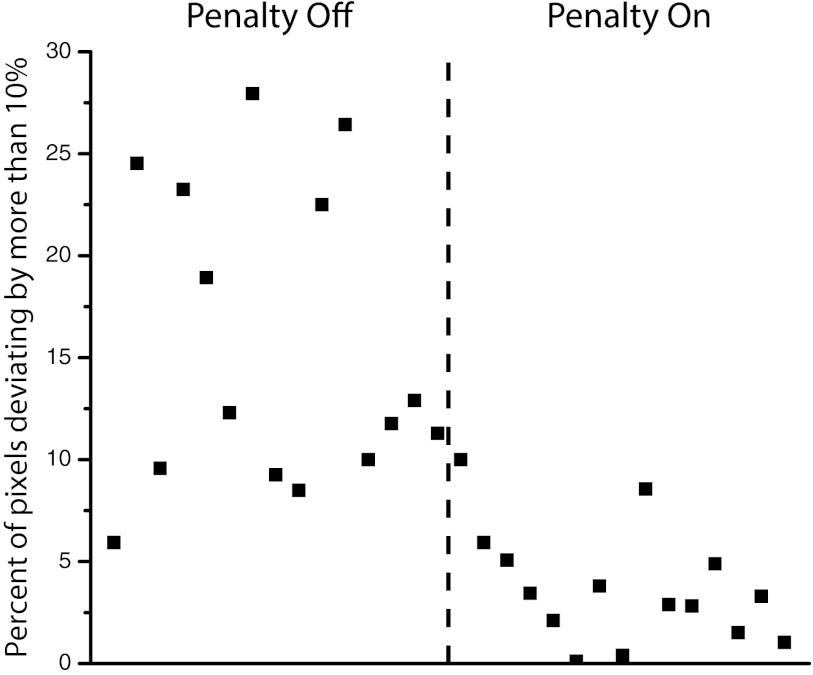
Film dosimetry was used to compare calculated and delivered doses for individual fields and composite distributions for two of the paraspinal plans: one without the penalty and one with the penalty turned on at a low weight of 3.1%. Figure 6 shows the error analysis of the EBT2 films for the 30 measured VMAT apertures. The plot shows the fraction of pixels whose absolute dose deviation is greater than 10%. The first 15 apertures do not have the edge penalty, and the second 15 have the penalty applied. We chose a fairly large threshold value of 10% because we do not apply any distance to agreement criteria or gradient compensation for this analysis, and errors on the aperture edges can easily exceed this value. The results in Fig. 6 show that adding the edge penalty to the optimization cost function dramatically reduces the number of pixels failing the 10% dose difference criterion.

Figure 6.

Percentage of pixels in each individual paraspinal aperture failing by more than 10% dose difference. The first 15 apertures have the edge penalty turned off, and the second 15 have the penalty turned on at a weight of 3.1%.

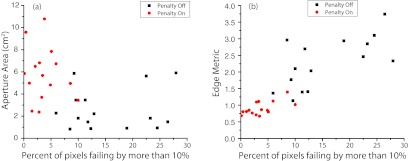
The measured errors shown in Fig. 6 allow the correlation of the error with various parameters related to the form of the aperture. In Fig. 7a, we attempt to correlate the measured error with the aperture area. This figure illustrates how the edge penalty both reduces the measured error and tends to make the apertures larger, but additionally shows that the correlation between the error and the aperture area is weak. In fact, some of the largest apertures in the plan with the penalty turned off also have the largest percent of pixels failing by more than 10%. This is a logical result since the aperture area alone cannot take into account the irregularity of the aperture shape. A much better correlation is found when comparing the measured error with the edge metric, as shown in Fig. 7b. This type of analysis could be used to set a threshold value for the maximum allowed edge metric value in a plan, or to determine the optimal values of C₁ and C₂ in Eqs. 1, 2.

Figure 7.

(a) Correlation of the aperture area with the measured error in the dose calculation for the measured paraspinal apertures. (b) Correlation of the edge metric with the measured error in the dose distribution.

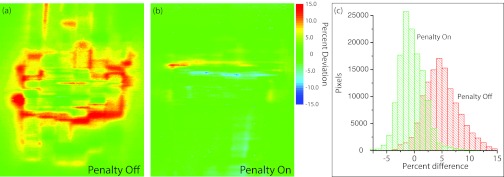
Figures 8a, 8b show dose difference maps of pixel percent deviation (calculation – measurement) for the plans without and with the edge penalty applied, respectively. Table 7 summarizes the results of the comparison between measured and calculated dose for these two plans using different agreement criteria. The number of pixels with less than 5% dose deviation in the composites is 52% (without penalty) and 96% (with penalty). The dose difference maps illustrate that the composite plan without the edge penalty had much higher errors compared to the plan with the edge penalty. Figure 8c shows the corresponding distribution of errors for each of the composite dose distributions in a histogram. The plan without the penalty has primarily positive deviations (calculation higher than measurement), whereas the plan with the penalty has deviations centered near zero and a narrower distribution. The mean and standard deviation of the percent dose difference for the plans without and with the penalty are 5.0 ± 3.2% and −0.5 ± 2.3%, respectively.

Figure 8.

(a) Dose difference map (calculation – measurement) for the composite film of the paraspinal plan without the edge penalty. (b) Dose difference map (calculation – measurement) for the composite film of the paraspinal plan with the edge penalty turned on at a weight of 3.1%. (c) Distribution of measured dose deviations for the two composite films.

Table 7.

Passing rates for the two measured paraspinal composite dose distributions with penalty off and on using gamma analysis and gradient compensation.

	Percent passing
Criteria	Penalty off	Penalty on
5%/0 mm	52%	96%
3%/3 mm gamma	97.5%	98.9%
3%/1 mm gamma	79.5%	95.4%
3%/1 mm gradient	83.3%	96.2%

Figure 8b shows that the inclusion of the edge penalty in the optimization results in much better agreement between calculation and measurement, with an even distribution of positive and negative dose differences, most of which are about 5% or less (corresponding to approximately 0.5 mm geometric differences in high gradient regions). In Fig. 8a it is evident that the calculation is hotter than the measurement at many points in the measured dose distribution. Possible explanations include tongue and groove effects on the y edges of the apertures, consistent geometric issues due to the fixed resolution of the MLC leaf descriptions, small delivery or MLC calibration problems, or the calculated penumbra for small apertures is slightly too wide. When larger, more regular apertures are used (e.g., in the plan with the edge penalty), the calculation is better able to predict the dose and the measured deviations become centered about zero.

DISCUSSION

We have developed an aperture regularization penalty to be used during inverse planning for VMAT. This “edge penalty” has been tested for paraspinal, brain, and liver cases. We have compared both plan quality (DVH analysis, various metrics) as well as accuracy of the dose calculation using EBT2 film. The addition of a low-weight edge penalty to the optimization cost function has the ability to remove unnecessary complexity in the optimized VMAT apertures while still creating a clinically acceptable plan. For our example paraspinal plan with a penalty weight of about 3.1% of the total cost function value after optimization, the aperture complexity was reduced by 55% with a corresponding increase in the dose-related cost function of just 1% compared to the plan without the penalty. DVH analysis shows nearly identical doses to all normal tissues with a small reduction in dose to the GTV. The brain and liver plans also had very similar results. While there are some small changes when the penalty is turned on, it is important to understand that when highly complex apertures are used, the dose calculation may be uncertain, meaning that the DVH curves shown by the solid lines in Fig. 4 may not accurately represent the delivered dose. The calculated DVH curves for the plan with the edge penalty are a much more reliable representation of the given plan.

Because individual optimized apertures in VMAT plans frequently do not cover the whole target volume, calculation errors on the edges of the apertures can build up and be compounded across the entirety of the target. This effect is magnified when apertures become more complex. The 55% reduction in aperture complexity for the paraspinal SBRT case with the edge penalty turned on allowed for a considerable increase in the plan accuracy, as shown by the EBT2 film measurements of the individual apertures and composite plans. For a 3%/1 mm gamma analysis, the percentage of pixels passing is increased from 79.5% to 95.4% when the edge penalty is turned on, and for gradient compensation using 3%/1 mm, the percentage increased from 83.8% to 96.2%. It is also notable that when 3%/3 mm criteria are used, the passing percentage is nearly identical for the two plans, even though the film analysis shows considerable discrepancies throughout the plan without the edge penalty applied. One should think critically about the criteria that are applied to specific treatment sites to ensure that these types of discrepancies between the calculated and delivered doses are not overlooked. This is particularly important for the evaluation of SBRT plans, which generally have small margins and high conformality. Gradient compensation over a small distance has the ability to highlight important dose differences related to algorithm and delivery related differences, as opposed to setup uncertainty and the finite calculation and measurement grids.²⁴

In addition to reducing aperture complexity, adding the edge penalty to the VMAT optimization process also improves delivery efficiency. This occurs through a reduction in the number of monitor units needed to deliver the plan, as well as through aperture regularization which reduces the required leaf motion during dynamic delivery. For this study, the VMAT plans were not delivered in dynamic mode, so an exact determination of the reduction in treatment time is not possible. For plans that have a high number of MU (SBRT plans, for example), the delivery time reduction will be very plan dependent because the leaf and gantry speeds will not be limiting factors in the delivery time. However, for other treatment sites that have a lower number of MU (where leaf motion and gantry speed may start to limit efficiency), the time savings is potentially even greater due to the reduction in leaf motion as well as MU. Because of the interplay of these effects, we expect that the improvement in delivery time will be case specific.

A method of reducing aperture complexity during the VMAT planning process is needed for the same reasons that intelligent smoothing can be beneficial for IMRT planning.^{15, 16} Complexity in inversely optimized plans accentuates the faults and the flaws in the planning system, and may not be required to produce a clinically acceptable treatment plan. Also similar to smoothing, reducing aperture complexity has the positive effect of reducing the MUs needed to deliver treatment. The edge penalty has the most dramatic effect when it is used for cases where the target is small, near (or overlapping) a critical structure, and nonspherical, since these are the cases where aperture complexity is most likely to be generated during optimization. However, the penalty is applicable for many different geometries, since irregular apertures are prevalent in VMAT plans regardless of target size and shape (for example, see the apertures shown in Refs. ²⁵ and ²⁶). The edge penalty can help prevent the optimizer from creating apertures that are too complex to allow for an accurate dose calculation. As long as the penalty is added at a weight that prioritizes the metric below critical structures, unnecessary complexity can be selectively removed during DAO. A weight of about 3% of the total cost function after optimization worked well for the three cases shown in this paper (although a range of penalty weights all produced acceptable plans). A weight of 3% corresponded to an initial weight of approximately 1% before optimization, however, this number is highly dependent on the initial setup of the plan as well as the form of the cost function used for optimization. It may be necessary to try a few different penalty weights before the desired compromise between plan quality and plan complexity can be found. We have found that after some initial experience with VMAT planning using the edge penalty, the desired penalty weight was often chosen on the first or second attempt.

The edge penalty presented in this paper could easily be added to existing optimization software for VMAT plans. The form of the edge penalty [the values of C₁ and C₂ in Eq. 2] can be chosen by comparing calculated and measured doses and correlating the edge metric with the determined error [as in Fig. 7b]. One advantage of the edge penalty being added to the optimization cost function instead of being used as an evaluation tool is that as long as the weight of the penalty is reasonable, no plan intervention is required after optimization. However, the edge metric can also be used as an evaluation tool in other settings. For example, we are currently investigating the use of the edge penalty to predict patient-specific IMRT QA failures.

CONCLUSION

We have developed and tested an aperture-regularization penalty (“edge penalty”) for volumetric modulated arc therapy plans. The addition of a low-weighted edge penalty has little effect on the optimized dose distribution, but has a clear positive effect on the generated apertures, the accuracy of the dose calculation, and the delivery efficiency. The results shown in this paper demonstrate that highly complex apertures are not always necessary to create high quality VMAT plans, but rather can be instead a consequence of the inverse optimization process. Adding the edge penalty at a low weight causes the optimizer to avoid irregularly shaped apertures when possible without compromising plan quality. The parameters of the edge penalty defined in Eq. 2 can be customized by the user, and the penalty could be easily added to existing VMAT treatment planning software.