Figure 3. Detecting quantum transport through a double quantum dot.

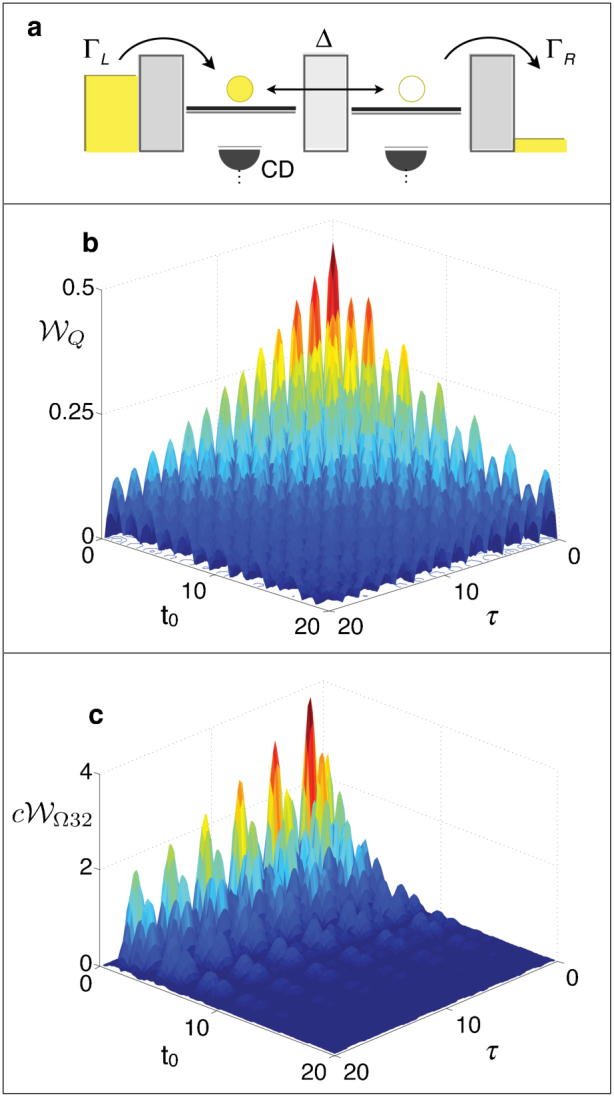
(a) Schematic of a single-electron double quantum dot (DQD). Here we assume that the DQD is weakly coupled to leads under a large bias. Its Hamiltonian is H_DQD = Δ(|L〉〈R| + |R〉〈L|) with the electron state basis {|L〉,|R〉,|0〉} where Δ is the tunnelling amplitude between the left-dot and right-dot electron states |L〉, |R〉. The transport between dots and leads is described by the self-energy, 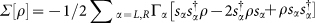, where s_L = |0〉〈L|, s_R = |R〉〈0|, and Γ_L and Γ_R are the left and right tunnelling rates, respectively. We assume charge detectors (CDs) are used for the measurements, but invasive current measurements are also sufficient (not shown here). (b,c) Verifying quantum transport through DQD with 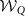[Eq. (4) for t − t₀ = τ] and 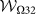[Eq. (6)], respectively. Here we define |0〉, |L〉, and |R〉 by |1〉, |2〉, and |3〉, respectively. For the setting Γ_L = 4, Γ_R = 0.1, and Δ = 1, the non-vanishe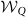d and 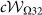indicate the quantum-transport regions, where c = (p₁p₂p₃)⁻¹ for the stationary state.