Figure 5. Detecting vacuum Rabi oscillations in a lossy cavity.

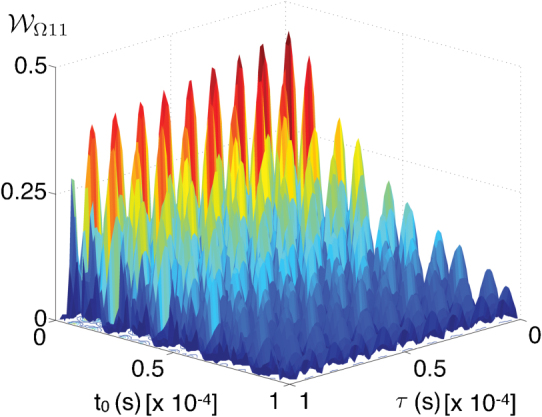
Here we use the experimental data reported in Ref. 47 to illustrate coherence-verification using our second witness Eq. (6). The circular Rydberg states with principle quantum numbers 51 and 50 for transition ω₀ = 51.1 GHz are considered as the states |e〉 and |g〉, respectively. The atom-field coupling is ω_R/2π = 47 KHz. For a high-Q cavity with Q = 7 × 10⁷, the vacuum Rabi oscillation is detected by use of 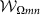where m = n = 1. As a comparison we also checked the case when the Q-factor is so low that 2ω_R < ω₀/Q. For such a low-Q cavity (e.g., Q = 7 × 10⁵), the state evolution is in the regime of irreversible transitions and obeys the classical constraint (3). Hence the value of the witness is zero.