Biaxial Compressive Strain Engineering in Graphene/Boron Nitride Heterostructures

Abstract

Strain engineered graphene has been predicted to show many interesting physics and device applications. Here we study biaxial compressive strain in graphene/hexagonal boron nitride heterostructures after thermal cycling to high temperatures likely due to their thermal expansion coefficient mismatch. The appearance of sub-micron self-supporting bubbles indicates that the strain is spatially inhomogeneous. Finite element modeling suggests that the strain is concentrated on the edges with regular nano-scale wrinkles, which could be a playground for strain engineering in graphene. Raman spectroscopy and mapping is employed to quantitatively probe the magnitude and distribution of strain. From the temperature-dependent shifts of Raman G and 2D peaks, we estimate the TEC of graphene from room temperature to above 1000K for the first time.

Graphene has attracted wide attention for both fundamental physics and potential application in electronics¹,²,³. Recently, hexagonal boron nitride (h-BN, abbreviated as BN in the following) has been proposed as an ideal substrate⁴,⁵,⁶,⁷,⁸ and tunnel barrier⁹ for graphene devices because it is atomically flat with little dangling bonds and charge traps. Devices based on graphene/BN (GBN) heterostructures have shown much higher mobility, less intrinsic doping⁴,⁵,⁶,⁷,⁸ and improved on/off ratio⁹ than conventional devices structures on SiO₂ substrate. On the other hand, because of the reduced interaction with substrate, GBN is also an appealing system to study intrinsic mechanical properties of graphene which has been rarely explored in GBN thus far. In particular, strain has been shown to effectively tailor the electronic properties of graphene for all-graphene electronics, pseudomagnetic field, and tunable bandgaps¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶. Recently, it is proposed that exploiting the different thermal expansion coefficient (TEC) between graphene and substrate could realize the desirable strain distribution for electronic device applications¹³,¹⁷. Experimentally, Bao et al. formed 1D ripple textures in suspended graphene¹⁷, while Yoon et al. achieved a uniform compressive strain ~0.05% in graphene on SiO₂ by thermal cycling¹⁸. However, the strain distribution in these systems were not well understood, which hinders the rational design of strain-based electronic devices.

Results

In this work, we utilize the different TEC of graphene and BN to engineer the strain in GBN heterostructures. After thermal cycling, large amount of triangular and polygonal graphene bubbles appear partly due to mechanical buckling under biaxial compressive strain. Finite element mechanical simulations show good agreement with experiments and reveal the strain distribution in the bubbles, which is further supported by Raman mapping. The spatially inhomogeneous strain distribution in graphene may be interesting for electronic device applications¹⁰,¹¹,¹²,¹³,¹⁴. Finally, we use Raman spectroscopy to quantitatively measure the temperature-dependent compressive strain in GBN due to TEC mismatch and derive the TEC of graphene over a wide temperature range.

Atomic force microscopy characterizations of GBN samples

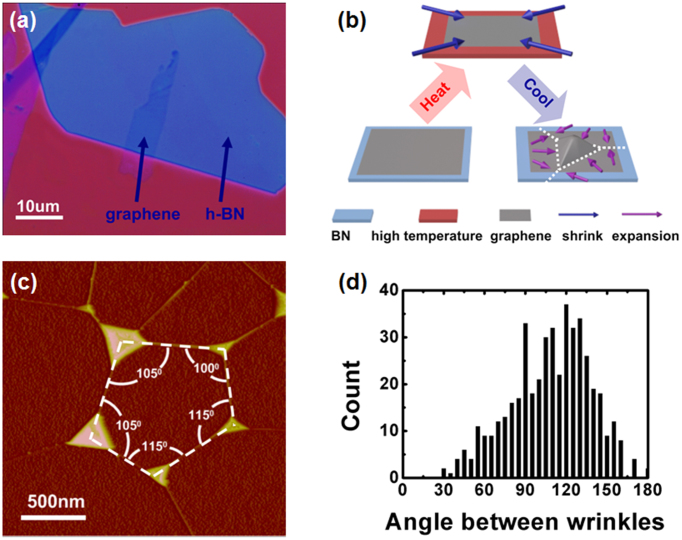
Single-layer GBN structures were made by a commonly used mechanical transfer technique⁴,⁷,⁸ (Fig. 1a, S1, the experimental details are described in Supplementary Information). We annealed the GBN in Ar atmosphere and employed atomic force microscopy (AFM) to characterize the samples. After annealing, we observed a large number of graphene bubbles,⁵ typically covering ≤~5% of the total area (Fig. 1c). The bubbles were interconnected by 1D ridges to form many 2D domains in the GBN. Statistical study showed that the average size and height of the bubbles were ~300 nm and ~23 nm respectively (Fig. S2), much larger than graphene bubbles observed on metal surface¹⁶,¹⁹. As a result, typical triangular bubbles in GBN introduced a much smaller pseudo-magnetic field on the order of 1T (Ref. ¹⁶). The angle distribution between the neighboring ridges peaked at 120 degree (Fig. 1d), which is likely due to the symmetric nature of the interaction between the hexagonal graphene and BN lattices. Previous studies have demonstrated that van der Waals interaction between two parallel hexagonal lattices shows triangular symmetry, with three energy minima forming 120 degree angles²⁰,²¹.

Figure 1.

(a) Optical image of a single-layer GBN sample on 300nm SiO₂. (b) Schematics of the proposed formation process of graphene bubbles and ridges on BN. (c) A representative AFM image of GBN bubbles and ridges after thermal annealing. Angles between the adjacent ridges are indicated. (d) Distribution of the angles between neighboring ridges showing a peak around 120 degree.

Raman spectroscopic study of GBN samples

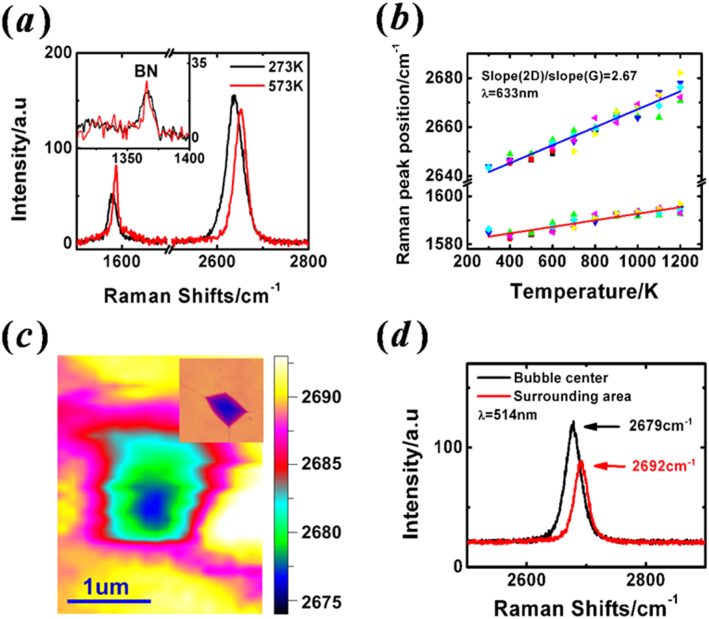
Raman spectroscopy is a powerful tool to investigate the mechanical and thermal properties of graphene²². For the as-made single layer GBN samples, three characteristic peaks appeared in the Raman spectrum ranging from 1300 cm⁻¹ to 2900 cm⁻¹, namely BN peak (~1366 cm⁻¹), graphene G peak (~1580 cm⁻¹) and 2D peak (~2640 cm⁻¹), without any defect-related peaks (Fig. 2a). We then gradually increased the annealing temperature of the GBN samples from 100°C to 900°C and did Raman mapping after each thermal cycling. Fig. 2a shows the typical Raman spectra of the same GBN as-made and after annealing at 300°C, with clear blue shifts of G and 2D peaks after annealing. Such measurements were repeated on seven samples (Fig. 2b). In order to minimize the effect of inhomogeneous strain distribution within the GBN⁷, each data point in Fig. 2b represented the average G or 2D peak position from a Raman mapping (typically a few hundred curves). We observed a linear temperature evolution of the peak positions, with different slopes for G and 2D peaks.

Figure 2.

(a) Raman spectra of the same GBN before and after 300C annealing.The inset compares the Raman peak of BN before and after annealing. The shifts in G and 2D peaks are not caused by system error as the BN peaks line up nicely for the two scans. We also carefully calibrated the spectrometer for each measurement. (b) Averaged G and 2D peaks positions of seven GBN samples as a function of annealing temperature. Solid lines are linear fittings of the data. The ratio between the linear temperature coefficient of 2D and G peak is 2.67. (c) A Raman mapping of 2D peak position near a graphene bubble with a 514 nm laser excitation. The bubble forms after annealing at 100°C. Inset shows the AFM of the bubble, sharing the same scale bar with (c). (d) The averaged Raman spectra taken at the bubble center and surrounding area from (c).

Two possible explanations for the peak evolution are compressive strain and charge doping²²,²³,²⁴,²⁵,²⁶. However, we rule out the possibility of charge doping because 2D peak shift is less sensitive to doping than G peak²²,²⁵, which contradicts our data. In addition, BN has been shown to introduce negligible charge doping to graphene⁴,⁵,⁶,⁷,⁸, which is not likely to shift the 2D peak by ~30 cm⁻¹ (Fig. 2b, Ref. 25). On the other hand, under biaxial strain 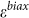, Raman peaks shift linearly as

where 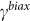is the Grüneisen parameter and 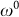is the unstrained peak position²². In the literature, the reported values of 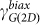show variations up to ~40%²². We adopted the values from ab-initio calculations in Ref. 27 (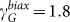, 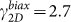) for quantitative analysis because they agreed well with experiments²⁸ and other calculations²⁹. We fit the peak evolution in Fig. 2b with linear function and obtained the linear coefficient

to be 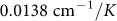and 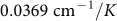for G and 2D peaks respectively. The ratio between the slopes (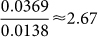) is in excellent agreement with the expected ratio of the pre-factors due to compressive strain 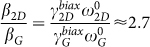. Therefore, we attributed the Raman peak evolution to compressive strain in the GBN after thermal cycling²². As expected, the strain was biaxial in nature as we did not observe any peak splitting over the entire temperature range²³.

Strain engineering is an effective way to tailor the electrical properties of graphene. Yet many interesting phenomena require carefully designed strain distribution in graphene¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶. The presence of bubbles introduces strain inhomogeneity that may enable unique strain-engineered devices based on GBN. To probe the strain distribution in GBN, we did Raman mapping on individual graphene bubbles (see Supplementary Information for details). Fig. 2c is the mapping of 2D peak position near the bubble shown in the inset. The bubble is clearly resolved together with the individual ridges extending from the corners (Fig. 2c inset). The 2D peak in the center is red-shifted by ~13 cm⁻¹ (therefore less compressively strained) compared to the surrounding area (Fig. 2d), which corresponds to 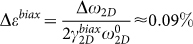. However, 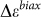is underestimated due to averaging effects since the size of the bubble (~400 nm × 300 nm) is much smaller than the laser spot size (~1 um). After considering the area fraction of the bubbles to the laser spot size, the effective 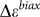is ~0.6%, consistent with our finite element modeling discussed below.

Finite element mechanical modeling of graphene bubbles

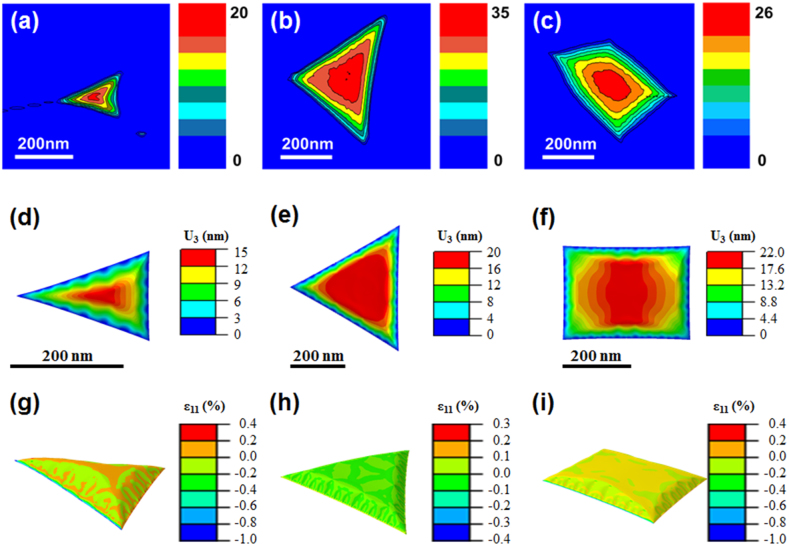
To understand the bubble formation and quantitatively capture the strain distribution in graphene bubbles, we conducted finite element simulations for typical bubbles observed in experiment (Fig. 3a–f. We approximated the experimental data to structures with high symmetry to capture the essential mechanics. The details of the finite element simulations are described in Supplementary Information). The bubbles exhibit great diversity in size, shape and topolography. The bubble in Fig. 3e (experimentally in Fig. 1c and 3b) was relatively flat or even slightly volcano-shaped with the center lower than the surroundings, because of the combined effect of multiple edge wrinkles. This is different from the bubble in Fig. 3d (experimentally in Fig. 3a), due to their different geometrical aspect ratios. The simulated out-of-plane displacements (Fig. 3d–f) closely resembled the deformation patterns and heights of experimental results (Fig. 3a–c). The edges in the simulated structures exhibited nano-scale wrinkle structures due to the extreme flexibility of monolayer graphene, although they were not clearly observed in experiments possibly due to limited lateral resolution of AFM. The strain distribution in the bubbles (Fig. 3g–i) is relatively uniform with magnitude close to zero, as the formation of bubbles release most of the compressive strains via nonlinear buckling mechanics. However, the strain is concentrated near the edges, because of the constrained strain release and wrinkle formation at the edges³⁰. Such strain distribution is consistent with our Raman mapping (Fig. 2c). The local strain at the edges is ~0.6%–1% for the simulated structures. The locally strained edges are similar to the structures studied in recent theoretical papers¹²,³¹. Although the strain is still too small to open bandgap for realistic devices¹², it can be further increased by decreasing bubble sizes (Fig. S3). In addition, the bubbles in GBN are much larger than those observed on metal surfaces¹⁶,¹⁹, therefore making electrical contacts to individual bubbles is possible.

Figure 3.

(a), (b) and (c) AFM height images of three representative bubbles with triangular and quadrilateral shapes respectively.(d), (e) and (f) The simulated out-of-plane displacements of the three bubbles shown in (a)–(c) respectively. (g), (h) and (i) Strain (ε₁₁, the normal strain along horizontal direction) of the simulated bubbles shown in (d)–(f).

Discussion

Bubbles were observed previously in GBN⁵,⁷,³², but the origin was still under debate. Possible explanation included trapped hydrocarbons⁷,³⁹, gas bubbles²⁸,³⁶ and pre-existing strain in graphene³². Recently, Haigh et al. brought direct evidence of hydrocarbons under graphene bubbles³⁹. Although we cannot rule out the possibility of hydrocarbons in our case, our Raman and finite element modeling suggest the biaxial compressive strain in graphene is also important in the formation of the bubbles (the detailed discussion of possible bubble formation mechanism is in supplementary information). Fig. 1b describes the possible formation process of the bubbles. Because of the weak interaction between graphene and BN, during heat-up, the graphene contracted and slided relative to the BN substrate due to TEC mismatch. During cool-down, the graphene expanded and experienced a biaxial compressive stress¹⁷,¹⁸. The bending stiffness of graphene (~1.4 eV)³³ is so small that slight compressive stress can cause graphene to buckle and delaminate away from the substrate at weak interfacial interaction locations, forming nano-scale bubbles and ridges. For such buckling mechanism under a constant strain, linear correlation between the height and size of the bubbles (Fig. S2c) is expected. We also carried out in situ AFM at elevated temperatures to study the bubbles at different temperatures. Fig. S5 shows the AFM of the same area during 50°C and 100°C annealing in ambient respectively. Many bubbles became smaller or even disappeared at higher temperatures, presumably due to contraction of graphene relative to BN. We note that the bubbles observed here are distinct from those owing to trapped gas on SiO₂ substrate²⁸,³⁶,³⁷, where the round-shaped bubbles form without any thermal treatment and experience tensile strain. It is well known that BN has a negative in-plane TEC from room temperature to 770°C³⁴. Therefore, the appearance of the bubbles indicates that graphene also has a negative TEC over a broad temperature range²⁹,³⁵, which is confirmed by molecular dynamics (MD) simulation (Fig. S4a, the details are in Supplementary Information).

The strain induced by TEC mismatch 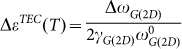could be estimated from Fig. 2b, where 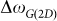is the Raman peak shift relative to the room temperature value. This can minimize the effect of pre-existing strain in graphene³². In Fig. 4a, we plot the temperature-dependent 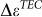derived from 2D peak evolution in Fig. 2b (G peak evolution gave similar results). In the case of small strain,

The linear temperature dependence of 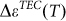up to 900°C (Fig. 4a) suggested a constant difference in the TEC of graphene and BN throughout the studied temperature range. Using the well-documented value of 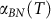by X-ray diffraction (up to ~800°C)³⁴, we can numerically derive that

as plotted in Fig. 4b. We note that Eq. (3) has two hidden assumptions. First, at the highest temperature of each thermal cycling, graphene is unstrained, which is valid if graphene were completely decoupled from the substrate. Second, the strain is not released during cool down. However, the finite (although small) interaction of graphene and BN and partial release of strain makes the derived TEC a lower bound. Even then, 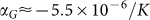at room temperature, well within the range of experimental values measured from suspended and supported graphene¹⁷,¹⁸, which suggest that Eq. (3) is still qualitatively valid in our analysis. However, the earlier experiments were unable to measure the TEC of graphene beyond ~400K. Our derived 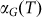shows a much weaker temperature dependence than the previous experimental results¹⁷,¹⁸ and agrees well with the first-principle calculations by Mounet et al. over a wide temperature range²⁹. In addition, we did MD simulations with Tersoff empirical bond order potential³⁸ to calculate the bond length of graphene up to 600K. The calculated bond length agrees well with both the first-principle calculations²⁹ and Eq. 4 (Fig. S4b). Possible sources of error in our analysis are discussed in the Supplementary Information.

Figure 4.

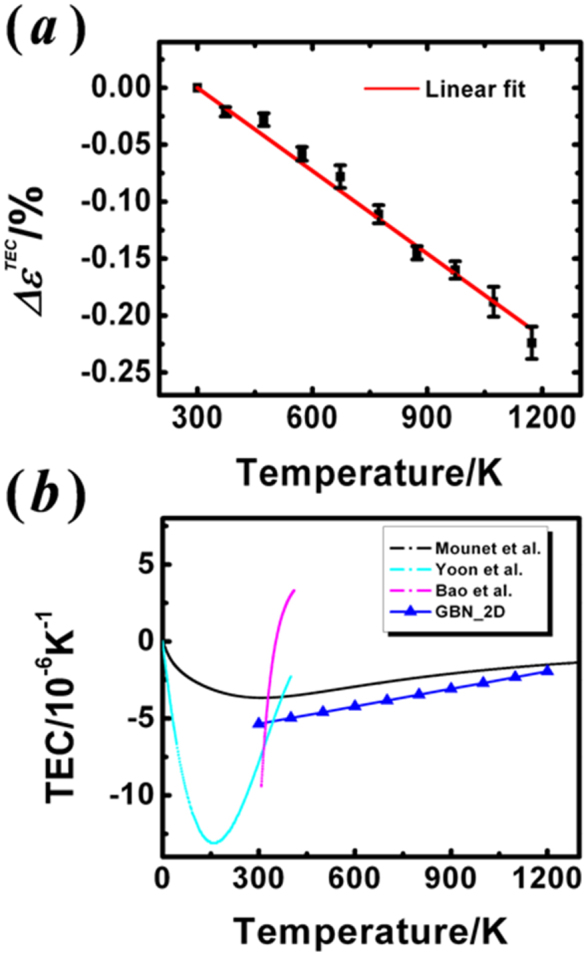
(a) 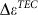as a function of temperature derived from the 2D peak shifts in Fig.2b. The red line shows linear fitting. (b) The temperature-dependent TEC of graphene derived from 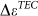, together with earlier theoretical and experimental results. The blue symbols are obtained from 2D peak shift in the present work (G peak shift gives similar results). The black line denotes the first-principle simulation results in Ref. 29. The purple and light blue lines denote the fitting of experimental values reported in Ref. 17 and 18 respectively.

In summary, we combined AFM, Raman spectroscopy and mapping, and mechanical modeling to study the biaxial compressive strain formation and distribution in GBN samples. Nano-scale bubbles appear partially as a result of mechanical buckling, creating interesting strain engineered graphene structures. Based on the strain evolution in GBN, we obtain the TEC of graphene over a wide temperature range, which agrees well with first-principle and MD calculations.

Methods

Fabrication and AFM characterization of GBN

We exfoliated single crystal BN flakes (~10 nm thick, ~100 μm in size) and single-layer graphene (Grade 300 Kish graphite, Graphene Laboratories, Inc.) onto separate 300 nm SiO2/Si substrates (Fig. S1a and S1b). The BN samples were annealed at 700°C in 5% H₂ in Ar atmosphere to remove possible organic contaminants. Optical microscope, Raman spectroscopy and AFM were used to confirm single-layer nature of graphene. After a brief baking step at 80°C, PMMA was spin coated onto graphene samples and subsequently baked at 180°C for half an hour. Then we carefully pasted a piece of Scotch transparent tape onto PMMA layer and etched the underlying SiO₂ by KOH aqueous solution, followed by thorough rinsing with DI water and careful drying at 50°C in an oven. Then the graphene/PMMA/tape sample was align-transferred onto the prepared BN flake. Finally the samples were carefully cleaned with acetone and isopropyl alcohol (Fig. S1c). AFM of the GBN samples was carried out in a Bruker Multimode 8 microscope under tapping mode.

Raman spectroscopy and mapping of GBN

Raman spectroscopy and mapping was done on a Horiba Jobin-Yvon HR800 confocal Raman microscope with a 633 nm He-Ne laser excitation and a liquid-nitrogen-cooled CCD detector (data from Fig. 2a and 2b in the main text). For each GBN sample, we usually mapped a 3 um × 3 um area with a 0.1 or 0.2 um steps. The mapping data in Fig. 2c and d was done using a 514 nm laser excitation. To avoid excessive heating effect on graphene, 2 mW laser power was used for all Raman measurements. We did AFM before and after Raman mapping to confirm that the bubbles were not damaged by the laser heating during Raman mapping.

Author Contributions

X. W., Y. S. and W. P. conceived the project. W. P., J. Z. and Z. N. carried out the experiments. J. X. did the finite element mechanical modeling. C. Y. and G. Z. did the molecular dynamics simulations. K. W. and T. T. provided the BN samples. W. P., J. X., Y. S. and X. W. co-wrote the paper. All authors reviewed and commented on the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information