Fluctuation broadening in carbon nanotube resonators

Abstract

We simulated the behavior of suspended carbon nanotube resonators over a broad range of temperatures to explore the physics of semiflexible polymers in underdamped environments. We find that thermal fluctuations induce strong coupling between resonance modes. This effect leads to spectral fluctuations that readily account for the experimentally observed quality factors Q ∼ 100 at 300 K. Using a mean-field approach to describe fluctuations, we analytically calculate Q and frequency shifts in tensioned and buckled carbon nanotubes and find excellent agreement with simulations.

The effects of thermal fluctuations can completely alter the mechanical properties of reduced dimensional systems. For example, the shape and elasticity of a DNA molecule are entirely dominated by thermal fluctuations of transverse degrees of freedom, completely altering both physical behavior and biological function. In overdamped environments such as liquids, these entropic effects have been studied for decades (1), but the behavior of reduced elastic objects in underdamped environments is largely unexplored. For example, consider a resonator made from an atomically thin membrane or polymer. How will thermal fluctuations affect the vibrational spectrum, and how will thermally driven nonlinear effects influence the decay widths of the resonance modes?

Carbon nanotube (CNT) resonators, with their nanometer-scale cross-section (2) and very small bending rigidity for flexural modes (3) present a unique opportunity to probe these questions. Experimental work has shown CNT resonators to be highly tunable (4) as well as functional as rf transceivers (5) and atomic mass detectors (6, 7), but these resonators have consistently exhibited much broader than expected decay widths (4, 8). Specifically, the quality factor Q, the key parameter measuring the degree to which an oscillating mode is decoupled from its environment, which is inferred from the decay width, is typically less than Q ∼ 100 at room temperature. These low Qs are not consistent with known dissipation mechanisms seen in other nanomechanical resonator systems (9). Analytical phonon-phonon scattering studies establish a theoretical upper bound on Q in CNTs that is well above experimental values, with Q ≲ 50,000 at 300 K (10, 11). Molecular-dynamics simulations of short CNTs (L ∼ 50 nm) show interesting behaviors in cantilevered and free CNT segments (12–15) due to anharmonic atomic potentials, and those that make an explicit determination of quality factor in thermal equilibrium (13, 14) give Q ∼ 1,000 at room temperature. Typically, however, experiments are performed on CNTs with L ≳ 1 μm, and the anharmonic elastic effects that dominate in short-length CNTs do not contribute as significantly at this longer length scale.

An alternative explanation for these altered properties comes from the field of polymer physics, where the effects of fluctuations on the physics of 1D elastic objects have a long and storied history. A key length-scale that characterizes these 1D objects' properties is the persistence length 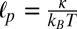, where κ is the bending rigidity. Subject to thermal forces, the 1D elastic object will fluctuate and lose correlations in shape for lengths longer than ℓ_p. Thus, short 1D structures (L ≪ ℓ_p) such as microfabricated nanobeam resonators behave like rigid rods, with thermal amplitudes small compared with the size of the structure. However, long 1D structures (L ≫ ℓ_p) such as organic polymers are forced into fluctuating, coiled, high-entropy configurations. Micron-scale CNTs are between these regimes, in the semiflexible polymer limit (L ≲ ℓ_p) (1), where the bending energy and configurational entropy contribute comparably to the total free energy. In overdamped environments, the behavior of semiflexible polymers is now well understood (16), but the behavior of a nanoscale resonator in the semiflexible polymer limit has not been explored.

In this article, we report simulations and analytical predictions of the thermally driven dynamics of CNT resonators over temperatures from 3 to 300 K and in the limits of both compressive and tensile strain. By simulating purely continuum elastic behavior, we isolate the specific influence of entropic forces on measured quantities, including both quality factor and thermally induced frequency shifts. Quantum mechanical effects are neglected, because the thermal occupation of all modes considered are in the classical limit. We find that the fluctuations of many resonance modes strongly influence the quality factor of CNT resonators, an effect called fluctuation broadening, which was previously invoked in the context of molecular spectra (17). We find that this fluctuation broadening is in good agreement with observed quality factors in experiment.

CNTs were modeled as 1D linear-elastic objects, with bending rigidity 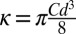and extensional rigidity K = πCd, where C ∼345 J/m² (18) is the 2D elastic modulus of graphene and d is the tube diameter. Each CNT was discretized into 100 or more masses joined by axial and torsional linear springs. For a given set of tube dimensions, boundary conditions, and externally applied forces, the equilibrium geometry was computed via a relaxation method, and zero-temperature eigenmodes were computed by diagonalizing the force constant matrix (19) (details in SI Text).

Results

To study dynamics at nonzero temperature, a finite time-difference calculation was used. Thermal equilibrium was reached by coupling the nanotube to an external heat-bath via a generalized Langevin equation, applying a stochastic white-noise force with external damping. Dynamics at equilibrium were then simulated with this Langevin equation using the fourth-order Runge–Kutta method. Adiabatic conditions were also studied using Stoermer’s rule (20). The model’s validity was confirmed by its ability to properly exhibit equipartition of energies for each eigenmode. Additionally, we performed externally driven simulations and found similar Q at low amplitude drive compared with the thermally driven simulation data we present.

Throughout this article, data are shown from simulations of a typical experimental case of a CNT with L = 3 μm and d = 2 nm. We investigate resonance properties of this CNT at different zero-temperature strains ɛ₀, temperatures T, and externally applied forces F_z by quasi-statically sweeping at most one parameter and measuring the power spectral density of the mean z-displacement (defined in Fig. 1A) of the nanotube: 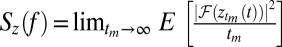, where t_m is the finite time over which the Fourier transform is taken, and E denotes an ensemble average. The mean z-displacement was the chosen parameter to analyze because it is typically measured in experiments (21). From S_z(f), we measure thermal frequency shifts Δf ≡ f − f(T = 0 K) and quality factor 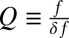. This definition of Q is used because the linewidth δ f is directly measured in experiments.

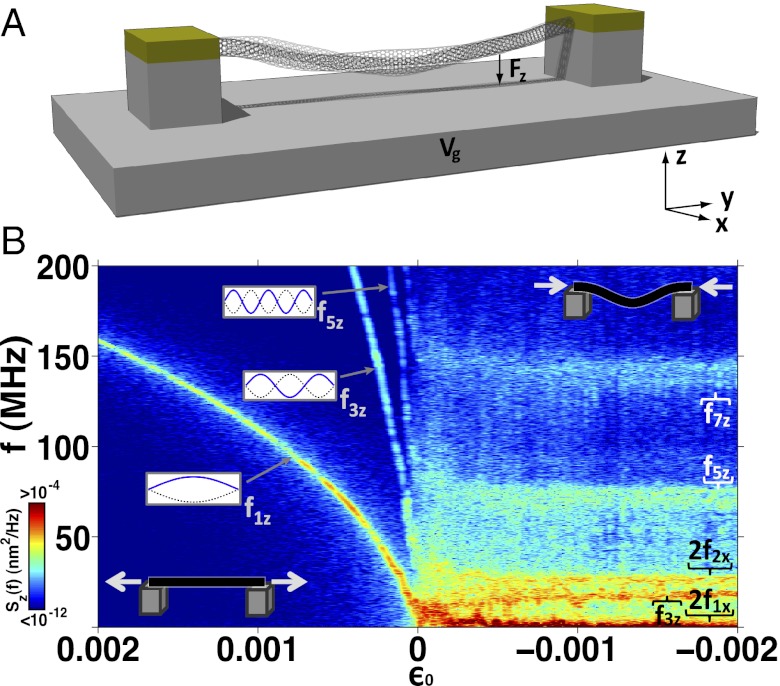
Fig. 1.

(A) Schematic of CNT resonator geometry. CNT is suspended between two electrodes (in yellow) and has a controllable downward force F_z electrostatically applied by a voltage to the underlying substrate. A small F_z is applied in B to keep the buckled tube oriented vertically. (B) Simulated power spectral density of the z-motion of the nanotube as a function of strain ɛ₀ at T = 100 K with logarithmic color scale. The tube is taken from tensile strain (Left) to compressive strain (Right) as illustrated (Insets). Eigenmode shapes are inset, as are labels for the eigenfrequencies.

We first study the qualitative behavior of this CNT as a function of strain at 100 K. In the tensioned limit (Fig. 1B, Left), the eigenmodes, labeled by their modeshape, tune like a tensioned string, giving a frequency , where μ is the linear mass density and n = Kɛ is the axial tension. Modes without mean z-displacements, including the even in-plane (z-direction) eigenmodes and all out-of-plane (x-direction) eigenmodes, are not visible. Thus, only modes with n = 1, 3, 5… are seen.

With negative strain, the nanotube undergoes a Euler buckling transition, as illustrated in Fig. 1B Upper Right. With the resulting built-in slack, the CNT can bend without stretching, leading the spectral lines to no longer tune significantly with strain. The linewidths, however, do tune with strain (Fig. S1). Also, there are emergent spectral lines corresponding to the motion of out-of-plane modes (Fig. 1B, Right). We analyze these temperature-dependent linewidths in the tensioned case and buckled case separately and discuss the different nonlinear coupling mechanisms (22–24) that apply to each.

Tensioned Nanotube.

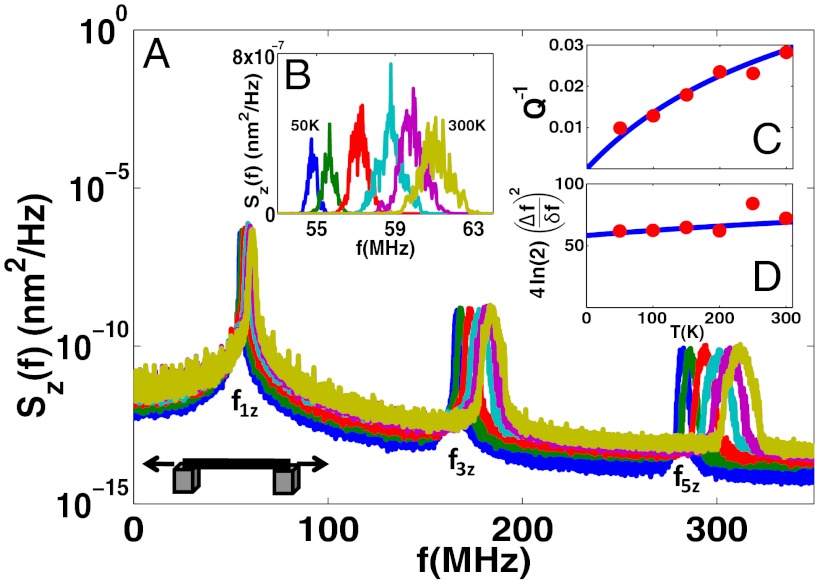
We begin with the tensioned case. We select a fixed tensile zero-temperature clamping condition ɛ₀ = 2 × 10⁻⁴, and simulate the nanotube motion at six temperatures, incrementing by 50 K from 50 to 300 K and plot in Fig. 2A the power spectral density over a frequency range spanning up to the n = 5 mode. The frequencies of the modes shift linearly with T and, as shown in Fig. 2C, the peaks also broaden with Q⁻¹ ∼ T. At 300 K, Q ∼ 40. The quality factor and frequency shifts can be understood to arise from the change in length of the CNT caused by thermal fluctuation in each eigenmode. The n^th eigenmode is given by , where ξ_na is the dimensionless modeshape with unit rms displacement, a_n is a time-varying amplitude function, and both the amplitude a and index a refer to either the x or y direction. The tube elongates by the length , where for each independent eigenmode; this leads to the strain being modified as , where brackets denote a time average over the period of oscillation (25). Assuming that 〈a_n〉 obey Boltzmann statistics in thermal equilibrium and that a_n fluctuate incoherently, we are able to solve for the mean strain shift and strain variance (details in SI Text).

Fig. 2.

(A) Power spectral density of a tensioned nanotube with ɛ₀ = 2 × 10⁻⁴. Six temperatures are plotted from 50 to 300 K spaced evenly in T. (B) Linear plot of S_z (f) for f_1z showing that the frequency shift Δf and line width δf both scale linearly with T. (C) Inverse quality factor of f_1z vs. temperature. (D) Dimensionless fixed ratio of Δf to δf that corresponds to n_f, the number of independent fluctuating modes contributing to spectral broadening and frequency shifts. In C and D, data are circles, and theory is a line. The line in C corresponds to Eq. 2, and in D n_f in Eq. 1.

In the high-tension limit, a large number of the resonance modes contribute significantly to length fluctuations. Accounting for the contribution of all resonance modes gives for the mean-field strain shift

where the value of is solved self-consistently, and n_f can be interpreted as the number of independent degrees of freedom causing significant length fluctuations. Here, high-frequency modes do not appreciably modify the strain, because most of their elastic energy is stored in bending rather than in stretching. is a length-dependent thermal expansion parameter that is distinct from the intrinsic thermal expansion simulated for CNTs (12). From Eq. 1, leads to Δf ∼ T.

Next, we calculate the strain variance , which leads to the prediction that δ f ∼ T. Furthermore, the predicted δ f constitutes fluctuation broadening and gives a unique prediction for Q (derivation in SI Text):

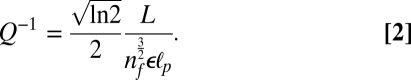Eq. 2 is our first key result. The dominant T-dependence comes from 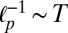, but both n_f and ɛ have weak T-dependence as a result of entropic stretching. The quantity 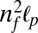is the persistence length for a tensioned beam and parameterizes how far fluctuations drive the CNT out of equilibrium. The 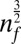dependence then can be understood to arise from an additional linewidth broadening 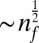due to averaging over n_f uncorrelated degrees of freedom. Eq. 2 accurately describes the numerical results, shown in Fig. 2C, and shows that fluctuation broadening can account for the experimentally observed Q ∼ 100 at room temperature (8, 21).

Buckled Nanotube.

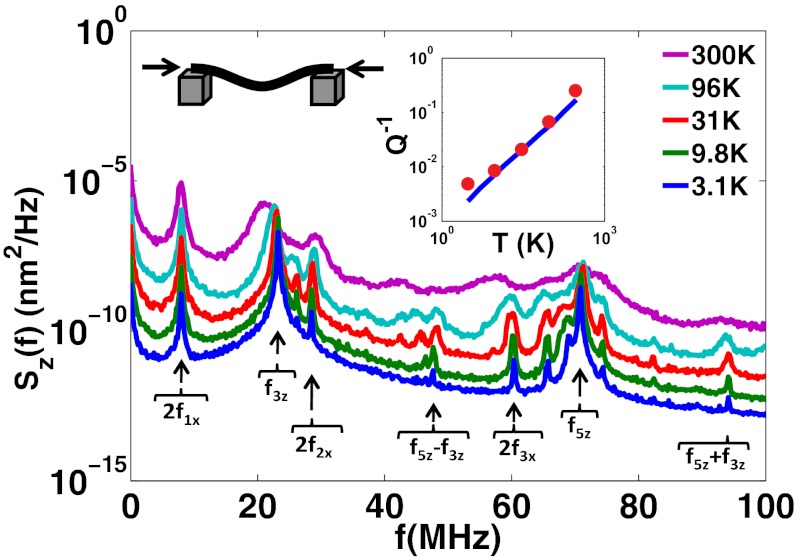
Next, we study a nanotube under compressive strain, picking ɛ₀ = −4 × 10⁻³. Applying a small downward force F_z = 0.6 pN that mimics the force applied by the gate in experiments, simulations were performed at logarithmically spaced temperatures from 3.1 to 300 K, as shown in Fig. 3. In contrast to the tensioned regime, there is complex structure in the spectra, with many spectral features growing nonlinearly with T. Linear theory predicts that f_3z and f_5z would be the only visible spectral lines in Fig. 3. The other emergent modes can be identified as either oscillations of out-of-plane modes producing z-displacement at twice their natural frequency (2f_1x, 2f_2x, and 2f_3x) or mixes of in-plane modes (f_5z − f_3z and f_5z + f_3z). Focusing on the lowest observed in-plane mode (f_3z), we observe Q⁻¹ ∼ T (Fig. 3, Inset) and a decrease in frequency with increasing temperature. From this we extract Q ∼ 5 for this mode at 300 K.

Fig. 3.

Power spectral density of buckled nanotube with ɛ₀ = −4 × 10⁻³ with F_z = 0.6 pN at logarithmically spaced temperatures. The built-in intrinsic damping dominates the apparent line width at the lowest temperature. (Inset) Plot of Q⁻¹ of the f_3z mode. Simulation data are shown as red dots, and theoretical predictions from Eq. 3 are plotted as a blue line. Labels beneath each spectral line correspond to their expected origin.

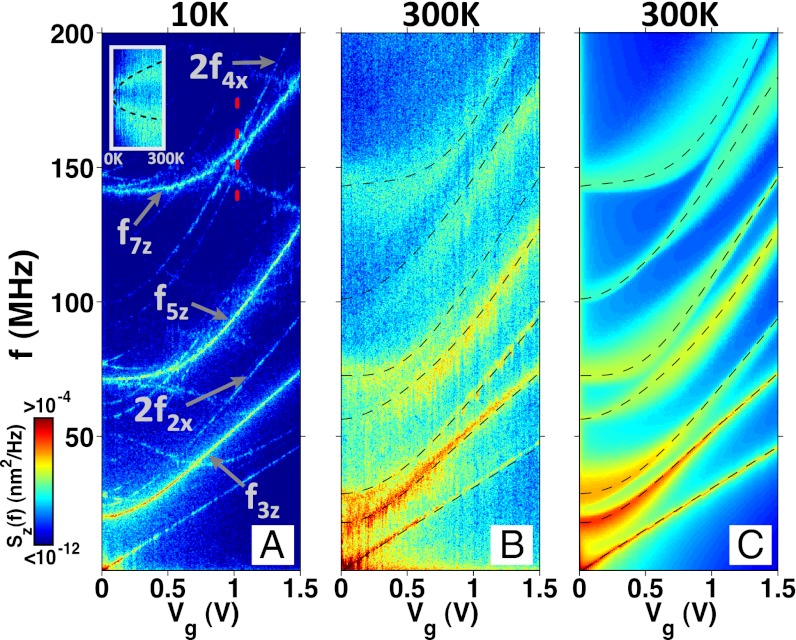
Further insight is gained by smoothly tuning frequencies by quasi-statically varying the magnitude of the electrostatic force 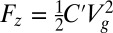, as shown in Fig. 4 A and B, where V_g corresponds to the electrostatic voltage applied to the gate illustrated in Fig. 1A, and 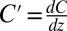is the derivative of the tube-gate capacitance assuming a 400-nm gap. The spectral lines tune with force and the frequency-doubled out-of-plane spectral lines cut across the in-plane spectral lines. At 0 K, linear theory predicts there to be no coupling. However, at the intersections, there are observable avoided crossings, even at 10 K, as seen in Fig. 4A. This behavior is consistent with experiments (21). To study this, we fix F_z at a crossing indicated by the dotted line in Fig. 4A, quasi-statically sweep the temperature, and measure S_z(f) (Fig. 4A, Inset). Here, we observe a sublinear T-dependence of the splitting at the avoided crossing. At 300 K, the frequency splitting is nearly one-fifth of the resonance frequency, indicating a strong coupling strength induced entirely by thermal fluctuations.

Fig. 4.

(A) Color map of power spectral density at 10 K of the mean z-displacement of a buckled nanotube resonator as a function of gate voltage, assuming tube is 400 nm above the gate. Modes are labeled as defined in Fig. 3, and color scale is identical to that in Fig. 1B. T-dependence from 0 to 300 K of the apparent avoided-crossing at 150 MHz is shown (Inset) at a fixed V_g indicated by the red dotted line. (B) 300 K data of same force sweep in A. (C) Plot of the theoretical power spectral density, based on the generalized version of Eq. 3 described in the text, for the same conditions as in B. The dashed lines in B and C correspond to the theoretical central frequencies from the generalized version of Eq. 3.

We build an analytical model for this behavior by first modeling the CNT as an inextensible object. In this framework, when an out-of-plane mode has finite amplitude, the CNT must move up in the z-direction to preserve length. To quantify the amount that the tube moves in z, we enforce the constraint that the differential length 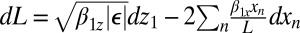is zero, where the equilibrium deflection of the tube is 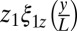. ξ_1z is a linear combination of in-plane modes, requiring to second order that 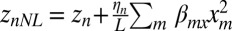, where 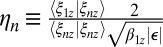, in which the brackets are an inner product defined by 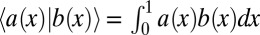(25).

Focusing on the interaction of one in-plane and one out-of-plane mode, we change the out-of-plane variable to 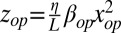and apply time-dependent perturbation theory (26) (details in SI Text) to generate a coupled set of linearized equations:

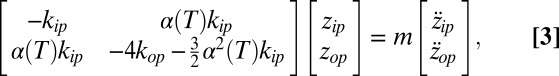where 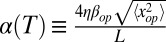and 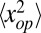is time-averaged over the period of oscillation.

Using 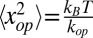gives 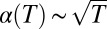, which when substituted into Eq. 3 predicts average frequency shifts. At an avoided crossing, k_ip ∼ 4k_op gives the prediction that 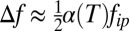; this matches the simulated T-dependence, as shown by the theoretical prediction that is overlaid on top of the data in Fig. 4A Inset.

By extending Eq. 3 to the full interaction matrix, populating each mode according to Boltzmann statistics, and weighting the resulting frequency probability distribution by the squared-amplitude distribution, we are able to generate a theoretical S_z (f) map, which is shown in Fig. 4C; it compares well with the simulated results at 300 K shown in Fig. 4B. In addition, the linewidths in the theoretical S_z (f) give an accurate prediction of the simulated Qs, as shown in Fig. 3 Inset. The specific degree of coupling is geometry-dependent, and thus not fully analytically generalizable, but Eq. 3 predicts for the lowest in-plane mode f_3z that

Eq. 4 (derivation shown in SI Text) explains the strain dependence of the spectral fluctuations seen in Fig. 1A Right: Q improves with increased buckling as the geometric coupling between modes decreases. Furthermore, due to its coupling with higher-frequency modes, the lowest in-plane mode is predicted to decrease frequency with increasing temperature at low V_g, which is frequently observed in experiment (7, 21).

Discussion

These results show that fluctuation broadening dominates the behavior of CNT resonators over a broad range of temperatures, and appears to be the main cause of temperature-dependent quality factors measured in both tensioned and untensioned resonators. Understanding the mechanism behind fluctuation broadening in CNT resonators draws on the ideas of polymer physics and underscores how thermal fluctuations can strongly modify the vibrational spectrum and decay widths in reduced dimensional nanoscale objects. To date there is limited experimental data characterizing Q over a broad temperature range in CNT resonators, but thus far, data remain at or below our theoretical upper bound (8, 21, 27). We predict a specific dependence of Q on ɛ₀ and T that can be tested by experiments that vary these parameters independently on individual CNT resonators. Specifically, varying ɛ₀ at a fixed T will be the most informative for this work, because the interpretation will be less obscured by systematic strain shifts that occur due to thermal expansion of the system.

This work implies a fundamental limit on Q in high aspect-ratio resonators at finite temperatures. Tailoring the geometry of these systems is necessary to mitigate thermally induced mode-coupling and thus improve Q.