Fig. 2.

Bistable circuit design. (A) Circuit encoding bistability. (B) Nondimensionalized equations of the simplified model: t_x is the scaled template concentration, and λ_x is the ratio of activator over inhibitor binding constant. Periods indicate multiplications. (C) Phase diagram of the bistable circuit in the {t_α, t_β} plane, with yellow indicating the bistable domain for {λ_α, λ_β} = {20, 20} and gray indicating the bistable domain for {λ_α, λ_β} = {100, 100}. (D) Same as in C, with yellow indicating the bistable domain for {λ_α, λ_β} = {100, 50} and gray indicating the bistable domain for {λ_α, λ_β} = {100, 100}. (E) Plot of the calculated trajectories of the bistable circuit for different initial {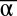, 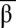} (small black dots). The bistable circuit is evolving to a stable state A (blue dot) or B (red dot). {λ_α, λ_β} = {100, 100} and {t_α, t_β} = {20, 20}, corresponding to the small circle in the gray area of C. (F) Same for {λ_α, λ_β} = {100, 50} and {t_α, t_β} = {10, 10}, corresponding to the small circle in the yellow area of D).