THE IMPORTANCE OF MICROSTRUCTURAL VARIATIONS ON THE FRACTURE TOUGHNESS OF HUMAN DENTIN

Abstract

The crack growth resistance of human dentin was characterized as a function of relative distance from the DEJ and the corresponding microstructure. Compact tension specimens were prepared from the coronal dentin of caries-free 3^rd molars. The specimens were sectioned from either the outer, middle or inner dentin. Stable crack extension was achieved under Mode I quasi-static loading, with the crack oriented in-plane with the tubules, and the crack growth resistance was characterized in terms of the initiation (K_o), growth (K_g) and plateau (K_p) toughness. A hybrid approach was also used to quantify the contribution of dominant mechanisms to the overall toughness. Results showed that human dentin exhibits increasing crack growth resistance with crack extension in all regions, and that the fracture toughness of inner dentin (2.2±0.5 MPa•m^0.5) was significantly lower than that of middle (2.7±0.2 MPa•m^0.5) and outer regions (3.4±0.3 MPa•m^0.5). Extrinsic toughening, composed mostly of crack bridging, was estimated to cause an average increase in the fracture energy of 26% in all three regions. Based on these findings, dental restorations extended into deep dentin are much more likely to cause tooth fracture due to the greater potential for introduction of flaws and decrease in fracture toughness with depth.

INTRODUCTION

Dentin is a mineralized tissue that occupies the majority of human teeth by both weight and volume. In the crown, dentin occupies the area between the pulp chamber and the Dentin-Enamel Junction (DEJ). One of the most distinct features of this tissue is the network of tubules (approx. 0.5 to 1.5 µm in diameter) that radiate outward from the pulp cavity to the DEJ [1]. Regarded as the dentin tubules, each is embodied by a collagen free, hyper-mineralized cuff of peritubular dentin. The interstitial space between the peritubular cuffs, i.e. intertubular dentin, consists of a collagen fibril matrix reinforced by nanoscale crystals of apatite [2, 3]. Based on this complex composition and microstructure, dentin is often regarded as a hierarchical biological composite.

Microscopic evaluations show that there are substantial spatial variations in the number, diameter and orientation of the tubule lumens in the tooth crown. These characteristics vary with distance from the pulp, physiology and traumatic history of the tooth [4, 5]. The tubule density and the tubule diameters are lowest at the DEJ and highest in deep dentin, nearest the pulp chamber [6]. Pashley et al [4] estimated that tubules occupied approximately 22% of the evaluated cross-sectional area near the pulp, and only about 1% near the DEJ.

Consistent with the microstructural variations about the tooth, the mechanical properties of dentin have been reported to vary widely with location [7–12]. Most early studies concerning spatial variations in mechanical behavior have concentrated on the hardness and strength, showing that there is a decrease in these two properties with proximity to the pulp. A recent evaluation of the fatigue behavior of coronal dentin [13] distinguished that that there is also a significant reduction in the fatigue crack growth resistance with distance from the DEJ. This aspect of the mechanical behavior is highly relevant to restorative dentistry as flaws are introduced within dentin during the cutting of cavity preparations [14]. Damage caused by cutting may coalesce into well-defined cracks and undergo cyclic extension [15, 16].

Fracture is one of the primary forms of restored tooth failure [17], and is often coined as the “cracked tooth syndrome” after [18]. This process is facilitated by cyclic crack growth and occurs when the crack length promotes a stress intensity that reaches the local fracture toughness of the tissue. Thus, spatial variations in the fracture toughness of dentin are important to the practice of restorative dentistry and treatment planning. An early study concerned with fracture of dentin [19] estimated a “work of fracture, W_f” using beams subjected to flexure loads, and found that W_f increases with proximity to the DEJ. But the aforementioned study did not evaluate the fracture toughness due to the absence of a well-defined crack. El Mowafy and Watts [20] were the first investigators to report the fracture toughness (K_IC) of human coronal dentin, finding an average of 3.08 MPa.m^0.5 for cracks aligned with the tubule orientation. It was later criticized that these experiments were performed on notched samples, rather than having sharp cracks, which can cause an overestimate of the toughness. Using sharp cracks with orientation perpendicular to the tubules, the fracture toughness was reported to be 1.8 MPa*m^0.5 [21]. Complimentary studies have analyzed the importance of lumen orientation [22, 23] and patient age [24, 25] on the fracture toughness, with values ranging from roughly 1 MPa•m^0.5 to over 2.5 MPa•m^0.5. The path of lowest crack growth resistance is perpendicular to the tubules and the fracture toughness of dentin decreases with patient age. However, no study has considered the importance of spatial variations in microstructure on the fracture toughness of dentin.

Most recent studies concerning the fracture behavior of dentin have reported that it exhibits a rising crack growth resistance with crack extension (i.e. rising R-curve) [22, 24–26]. This is an important quality, and is exhibited by most materials with hierarchical microstructure [27, 28]. A number of studies have evaluated the process of crack extension in dentin and the mechanisms contributing to toughening [26, 29–32]. These studies have argued that dentin is primarily extrinsically toughened, and is achieved largely by crack bridging by uncracked ligaments of tissue [25, 31, 32]. But an alternate evaluation of fracture in dentin suggests that inelastic deformation arising from the organic content plays a major role in the fracture process, and that the toughness should be estimated using elastic-plastic fracture mechanics [33]. Owing to the spatial variations in microstructure of dentin, both theories could be correct, albeit applicable to different regions of the tooth.

In this investigation we evaluated the influence of microstructure on the fracture toughness of human dentin using a conventional fracture mechanics approach. A hybrid method was also adopted, involving a combination of experiments and numerical modeling, to estimate the relative contributions of extrinsic and intrinsic toughening mechanisms to the site-specific crack growth resistance. The primary objectives were to quantify the spatial variations in fracture toughness of coronal dentin and to develop a mechanistic understanding of the fracture process related to the microstructure.

MATERIALS AND METHODS

The experimental evaluation was conducted using the coronal dentin of caries-free unrestored 3^rd molars, which were obtained from young dental patients in Maryland (16≤age≤28 years). The teeth were extracted according to protocols approved by the Institutional Review Board of the University of Maryland Baltimore County (approval Y04DA23151) and stored in Hank's Balanced Salt Solution (HBSS) with record of patient age and gender.

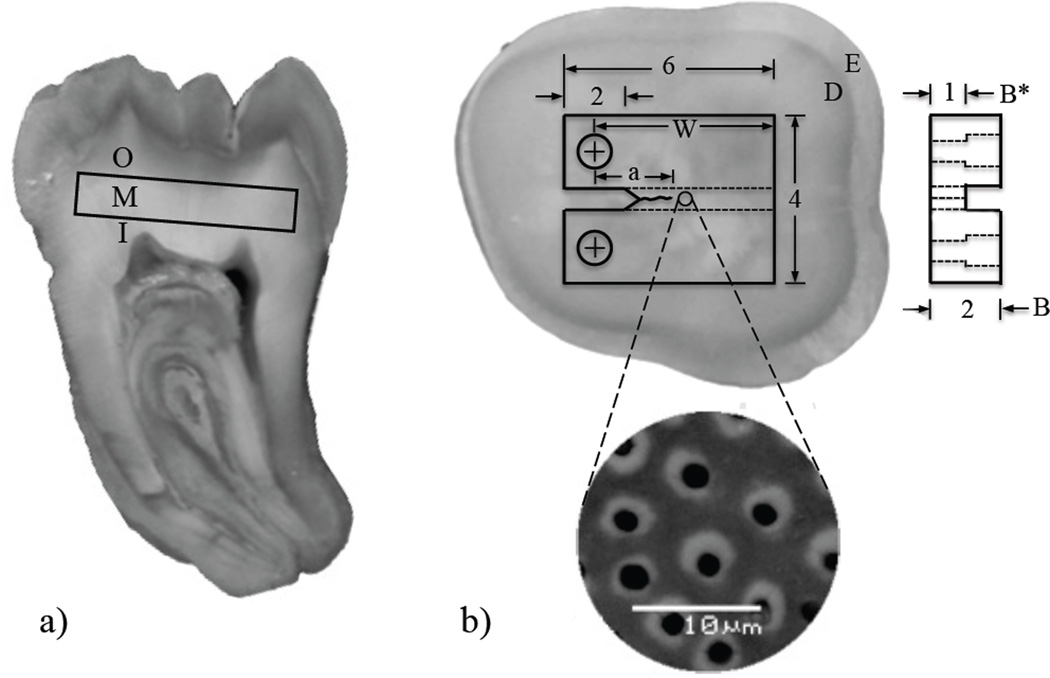
Within one month of extraction a Compact Tension (CT) specimen was wet sectioned from each tooth using a numerical controlled slicer/grinder (Chevalier, Model SMART-H81811, Taiwan), and diamond abrasive slicing wheels. The specimens were prepared to achieve crack growth in-plane with the dentin tubules (0° orientation) but perpendicular to their length as detailed in Figure 1. Primary sectioning was performed to obtained specimens from the peripheral (N=4), middle (N=4) and inner (N=4) regions of the teeth, which were located approximately 0.5 mm, 2 mm and 3.5 mm away from the DEJ, respectively (Figure 1(a)); a total of 12 specimens were prepared for testing. Secondary sectioning was performed to establish the body of the specimen (Figure 1(b)) and introduce other aspects of the detailed geometry. Briefly, a 1 mm wide channel was introduced on one side of each specimen to guide the direction of crack extension and precision holes were counter-bored using a miniature milling machine to enable application of opening mode (Mode I) loads. Then, a sharp notch was introduced using a razor blade and a diamond particle paste (1µm diameter) to facilitate crack initiation. The protocols used in preparing the dentin CT specimens have been described in more detail elsewhere [34, 35].

Figure 1.

Preparation of a compact tension (CT) specimen machined from a human 3rd molar. (a) section of a human 3rd molar indicating the three coronal regions where the specimens were obtained. I, M and O represent inner, middle and outer, respectively; (b) view of a sectioned tooth and potential specimen. The dentin (D) and enamel (E) are evident from the difference in gray scale. Note that the crack front is in-plane with the tubules, but perpendicular to their axes.

A fatigue pre-crack was introduced at the notch tip of the specimens to avoid effects of the notch radius [21]. Mode I cyclic loading of the CT specimens was performed for the crack initiation process using a universal testing system (Bose, Model ELF3200, Eden Prairie, MN, USA) with stress ratio (R) of 0.5, frequency of 5 Hz and using loads of 14≤P≤25 Newtons. All loading was performed within an HBSS bath at room temperature (22°C). After initiation, the crack was extended approximately a≤0.5 mm from the notch tip. Stable crack growth experiments were conducted using a dedicated universal testing system complemented with a microscopic imaging system [35]. Quasi-static loading was performed using displacement control at 0.1 mm/min and with 1 N load increments, until the onset of crack extension. Thereafter, incremental crack extension was achieved using 0.5 N load increments until the crack reached the point of instability. Hydration of the samples was maintained during loading using a saturated cotton swab “cradle” that was nestled beneath the specimen and retained moisture from an eyedropper of Hanks’ Balanced Salt Solution (HBSS).

A sequence of digital images was acquired during each increment of quasi-static loading using a stereomicroscope (Optem zoom 70×l 391940, QIOPTIQ, Luxembourg) until the specimen fractured. The images were used to interpret the displacement field and crack lengths using Digital Image Correlation (DIC). To facilitate application of DIC, the surface to be viewed under microscopy was subjected to a surface treatment with an air jet to deposit speckles of black paint. The process resulted in a grayscale distribution suitable for microscopic DIC and analysis. The digital images were processed using dedicated software to quantify the crack length and the crack opening displacement (COD). The application of microscopic DIC has been described in detail elsewhere [36].

In the evaluation of crack growth, the crack tip was defined as the point of zero opening displacement, and the crack length “a” was calculated from the distance between the opening load application and the crack tip. The opening mode stress intensity (K_I) distribution with crack extension was calculated according to [34]

$${\mathrm{K}}_{\mathrm{I}}=\frac{\mathrm{P}}{{\mathrm{B}}^{*}\sqrt{\mathrm{W}}}{\left(\frac{{\mathrm{B}}^{*}+1}{\mathrm{B}+1}\right)}^{0.5}(0.131+0.320\mathrm{\alpha }+0.211{\mathrm{\alpha }}^2)$$ (1)

where P is the opening load, α is the ratio of a to W (Fig. 1(b)), B is the specimen thickness and B* is the specimen thickness adjacent to the back channel. Equation (1) is valid for crack lengths between 1.4 mm and 3 mm.

Following the crack growth resistance experiments, the specimens where dehydrated in air for a day, and then sputtered (Model LLC Desk II, Denton vacuum, Moorestown, NJ, USA). The fracture surfaces were analyzed using a Scanning Electron Microscope (SEM; JEOL JSM 5600, JEOL Inc., Peabody, MA) under both secondary electron imaging (SEI) and backscatter emission (BSE) modes. The microscopic analysis was performed to identify mechanisms responsible for toughening of dentin. In addition, the images were analyzed using public domain software (Image J 1.42i, National Institutes of Health, Bethesda, MD, USA) to quantify the lumen density, the area occupied by the lumens and the peritubular cuff thickness [37]. Briefly, the BSE images were treated using a threshold scheme in order to distinguish between the lumens, cuff and the background material. Then, the lumens were counted and the area occupied by the lumens and peritubular cuff were calculated using the particle analyzer routine in Image J. The software calculates area as the number of pixels forming the designated particles. Thereafter, microstructural features of dentin were correlated with the measurements of crack growth resistance.

Finite Element Model

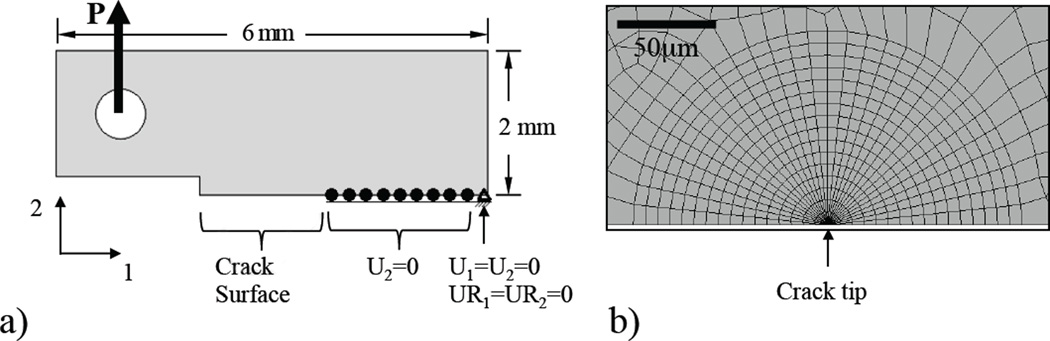
Crack growth toughening in dentin has been described in terms of extrinsic and intrinsic mechanisms [22, 32]. Extrinsic mechanisms act primarily behind the crack tip and reduce the amount of energy that is available for crack extension, whereas intrinsic toughening is essentially an inherent property of a specific microstructure and operates ahead the crack tip. To quantify the contribution of intrinsic and extrinsic mechanisms to toughening, a hybrid approach was adopted where results of the aforementioned experiments were used as the solution for a final element model that accounted for the fracture process. A 2-D half model for the dentin CT specimen was developed (ABAQUS/Standard, Version 6.9, Dassault Systèmes, Vélizy-Villacoublay, France) with dimensions equivalent to the specimen geometry shown in Figure 1(b). The model (Fig. 2(a)) was comprised of approximately 2,500 elements and 7,500 nodes and meshed with 8-node quadrilateral plane strain elements with reduced integration points (CPE8R). The crack was defined on a symmetry plane, requiring that only one crack face was modeled, and a symmetry constraint was applied to the intact cross section (without crack). An opening load was applied at the center of the hole by a rigid ring (Figure 2(a)) with magnitude of the applied load (15N<P<25N) defined according to that used during the experiments. At the crack tip the mesh consisted of concentric arcs of quadrilateral elements collapsed down to triangles and focused toward the center as shown in Figure 2(b). This approach to meshing allows singularity at the crack tip, and a smooth transition between the region requiring fine mesh and the coarser mesh further away.

Figure 2.

Finite element model details. (a) geometry, boundary conditions and loading, and (b) crack tip mesh (element type CPE8R).

The material behavior definition for dentin accounted for both elastic and inelastic deformation. Elastic deformation was modeled with modulus of elasticity and Poisson’s ratio of 19 GPa and 0.3, respectively [3]. Inelastic deformation was modeled using the Ramberg-Osgood description for material behavior according to [38]

$$\mathrm{\epsilon }=\frac{\mathrm{\sigma }}{\mathrm{E}}[1+\mathrm{\alpha }{\left(\frac{\left|\mathrm{\sigma }\right|}{{\mathrm{\sigma }}_{\mathrm{o}}}\right)}^{\mathrm{n}-1}]$$ [2]

where σ is the stress, ε is the strain, E is the Young's modulus (19 GPa) and σ_o is the yield stress (75 MPa). The constants α and n are the yield offset and the hardening exponent, respectively, which were determined from fitting the stress–strain curve of Sano et al [39] to the Ramberg– Osgood power law relationship. Using this approach, the constants are α=0.56 and n=5.5.

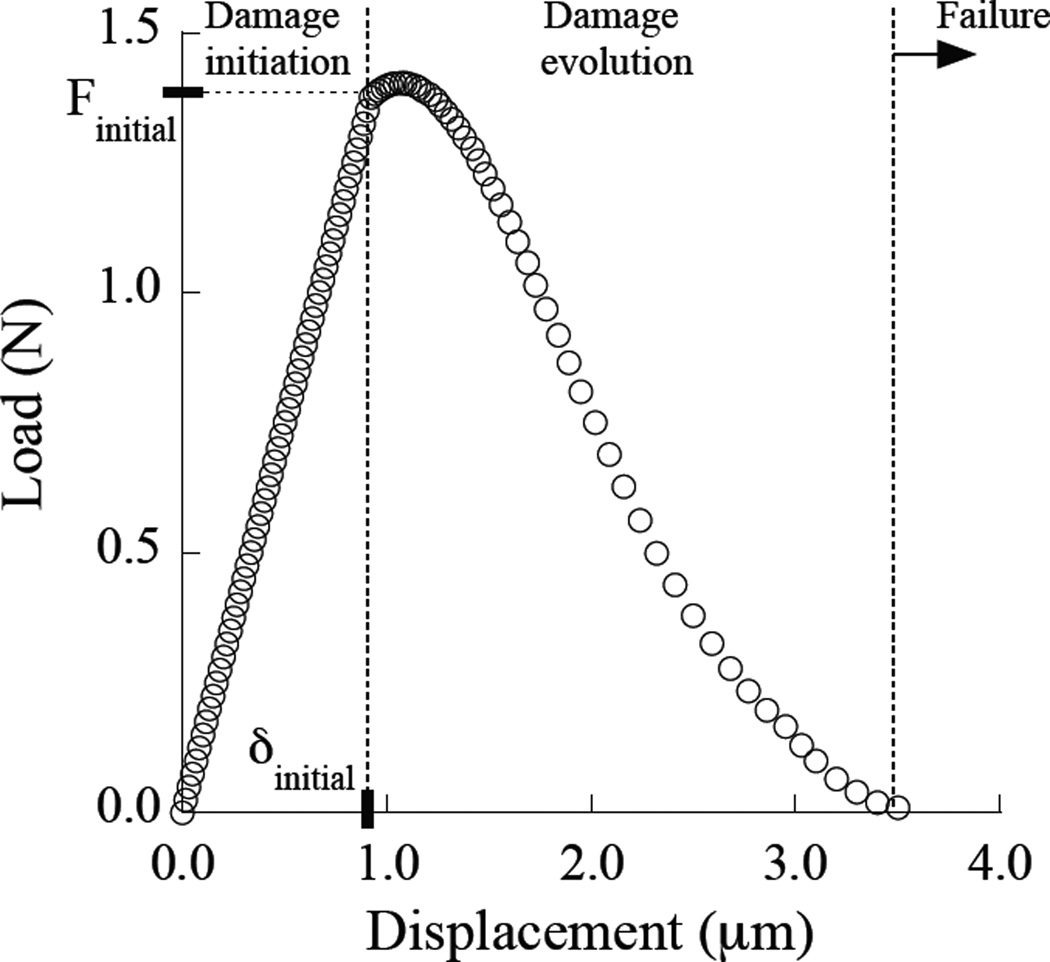
To account for extrinsic toughening a cohesive zone was introduced with a series of nonlinear spring elements located behind the crack tip. The length of the cohesive zone was defined based on experimental observations, ranging from 100 µm to 500 µm. Overall, the springs consisted of three components of behavior including damage initiation, damage evolution and failure as shown in Figure 3. According to the experiments it was found that the toughening behavior reached a plateau after approximately 0.3 to 0.5 mm of crack extension, defined from the point of initiation under quasi-static loading. At that distance from the crack tip the average opening displacement determined in the experiments (from the crack mid-line) was approximately 3.5 µm Therefore, the maximum displacement allowed for the springs was 3.5 µm. The number, distribution and stiffness of the springs were determined using an inverse approach. Experimental measurements of the near-tip COD distributions were used as a solution for stable crack growth simulated using the finite element model. The final constitutive behavior of the springs was determined using an iterative process. Briefly, the constitutive behavior of the springs was modified until reaching agreement between the experimental and the numerical COD profiles within a 5% difference. A total of three finite element models were developed, one for each coronal region (i.e. inner, middle and outer dentin). The crack length and applied opening load used in specific simulations were defined from experimental data at the position of crack extension corresponding to the plateau toughness, where the toughening mechanisms were fully developed.

Figure 3.

Constitutive behavior of the springs used to model extrinsic toughening. Notice that the maximum elongation of the spring is 3.5 µm.

After achieving agreement between experimental and numerical COD profiles, the J-integral for each specimen was estimated using the finite element model. The J-integral was evaluated numerically along a set of 15 contours surrounding the crack tip [40]. The energy consumed by ligaments bridging the crack and during elastic and plastic deformation was calculated using the finite element model. Each of the energy components was obtained separately. The total J-integral was calculated according to

$${\mathrm{J}}_{\text{total}}={\mathrm{J}}_{\text{el}}+{\mathrm{J}}_{\text{tip}}+{\mathrm{J}}_{\text{brid}}$$ [3]

where J_el corresponds to the J integral due to elastic deformation only (i.e. LEFM), J_tip accounts for the energy spent in plastic deformation ahead of the crack tip (intrinsic toughening), and J_brid quantifies the energy exhausted by work of the ligaments behind the crack tip that are represented in the model with springs (extrinsic toughening). In the last step of the simulation, the normal stress at each spring location was found as the remaining force in the spring divided by the cross-section area over which it acts. Then, J_brid was calculated from the area under the curve of the normal stress as a function of the spring’s y-displacement. The apparent toughness was estimated using the J-integral values according to [40]

$$\mathrm{K}=\sqrt{\mathrm{J}·\mathrm{E}\text{'}}$$ [4]

where J is either J_el or J_total for the linear elastic (K_c) and effective (K_eff) fracture toughness, respectively and $\mathrm{E}\text{'}=\frac{\mathrm{E}}{1-{\mathrm{\nu }}^2}$ according to the specimen dimensions meeting plane strain conditions [40]. It is important to note that K_eff is the “effective” toughness that accounts for contributions of the elastic and inelastic deformation, as well as extrinsic toughening. Using the individual components of energy related to deformation and the toughening mechanisms the relative contribution of the intrinsic and extrinsic mechanisms to the toughness was estimated in each of the three regions of coronal dentin evaluated.

RESULTS

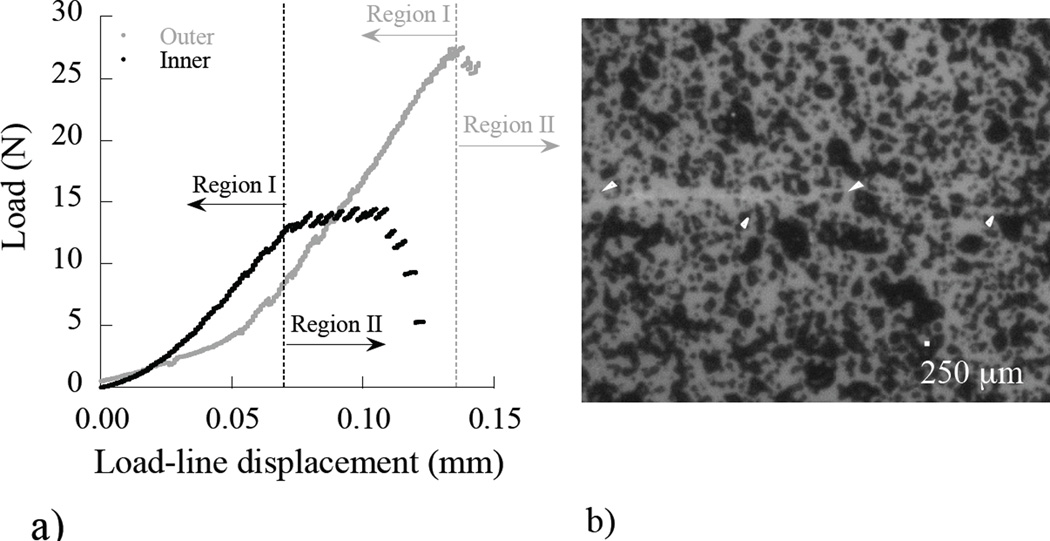
It was apparent from the opening mode loads required to achieve crack growth that there were differences in the fracture behavior of dentin specimens obtained from the three regions. A comparison of the loading history documented during crack initiation and stable crack extension in selected CT specimens is shown in (Figure 4(a)). Those specimens prepared from outer dentin required loads approximately 50% greater than those for inner dentin to achieve crack growth. At each increment of loading a digital image of the region embodying the crack was obtained for image processing using DIC and identification of the crack tip (Figure 4(b)).

Figure 4.

Quasi-static loading response and crack extension in the dentin. (a) a load-line displacement distribution for stable crack extension. Region I entails crack opening and the initiation of growth. Region II corresponds to incremental stable crack extension; (b) a digital image of a crack in a dentin specimen and the gray scale distribution used for the DIC analysis. Note the crack path highlighted by the white arrows.

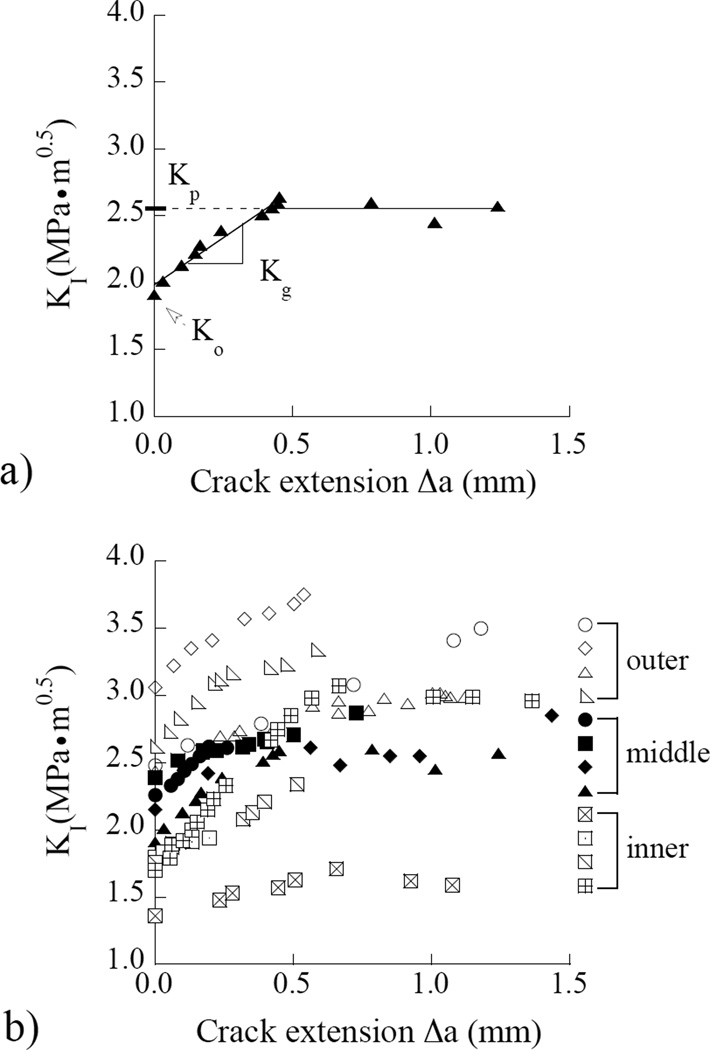
The load and crack length history corresponding to stable crack extension (Region II) were used to develop fracture resistance curves. A representative crack growth resistance curve (i.e. R-curve) obtained for a CT specimen from middle dentin is shown in Figure 5(a). There is an increase in the crack growth resistance with crack extension, which was exhibited by specimens from all three regions evaluated. Consequently, the responses were quantified in terms of the initiation toughness (K_o), followed by the increase in resistance to crack extension (K_g) as shown in Figure 5(a). The plateau toughness (K_p) was defined at the plateau in crack growth resistance (as evident in this figure) or at the maximum value of stress intensity for those specimens that failed to reach a plateau; it is also regarded here as the fracture toughness (K_c). The crack growth resistance curves for all the specimens are shown in Figure 5(b). Stable crack extension initiated at a stress intensity of 1.35 MPa•m^0.5 or greater in all specimens (1.35≤ K_o ≤3.05 MPa•m^0.5) and the growth toughness ranged from 0.5≤ K_g ≤ 2.2 MPa•m^0.5. The maximum crack growth resistance ranged from approximately 1.6 ≤ K_p ≤3.7 MPa•m^0.5 considering all the specimens evaluated.

Figure 5.

Crack growth resistance (R-curve) responses for the dentin specimens. (a) a typical Rcurve for young dentin obtained from a 23 year old female. The initiation (Ko), growth (Kg) and plateau (Kp) toughness defined in this response. (b) results obtained from all of the specimens an in all three coronal regions evaluated.

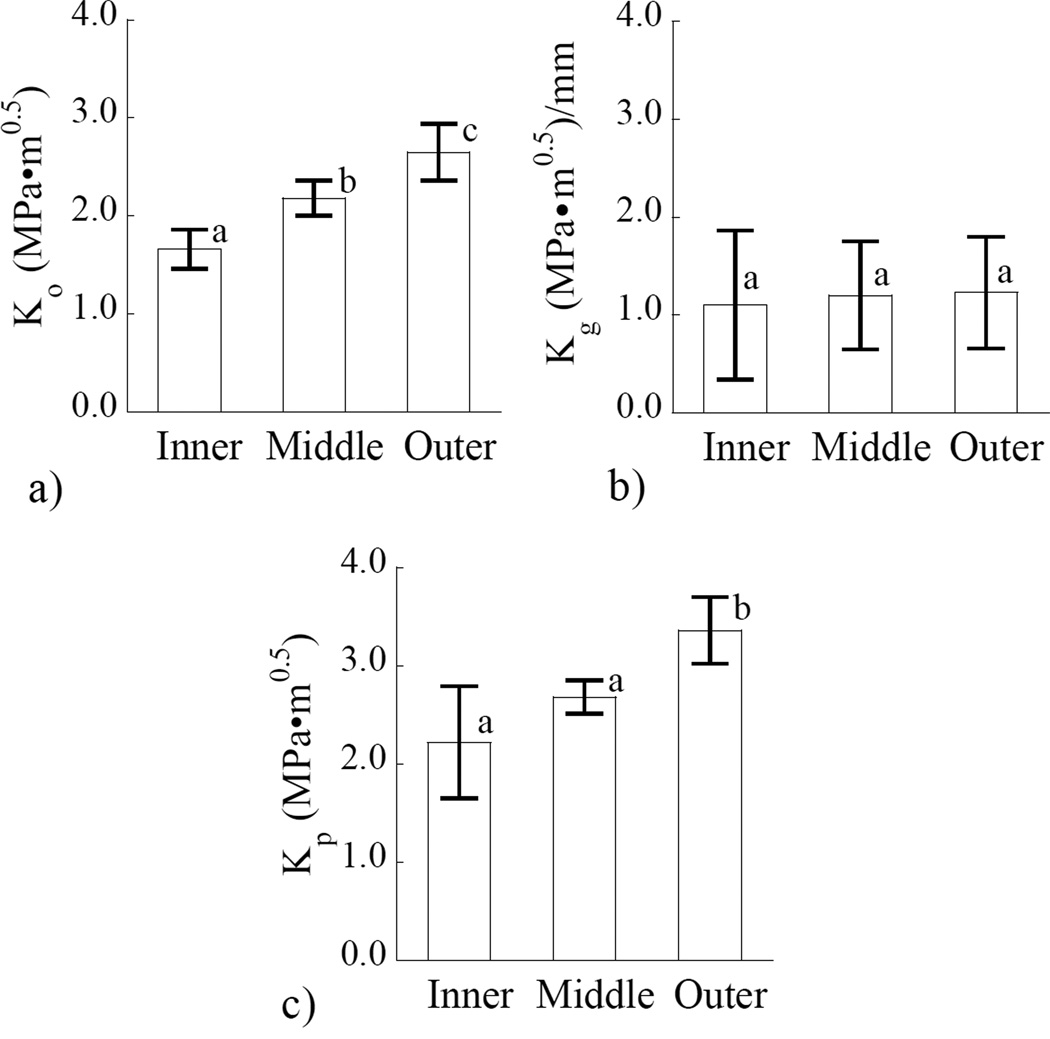
A comparison of the three components of crack growth resistance obtained for the three regions of coronal dentin is shown in Figure 6. Results obtained for K_o (Figure 6(a)) show that there is a significant difference (p≤0.04) between the driving forces required to initiate crack extension in each of the three regions evaluated. It is important to note that K_o for the outer dentin (2.65±0.29 MPa*m^0.5) is approximately 60% higher than that for inner dentin (1.66±0.2 MPa*m^0.5). In comparing the values of crack growth toughness (K_g) in Figure 6(b), no significant difference was found between the values obtained from the three separate regions. Although there was also no significant difference (p>0.05) between the values for K_c obtained for the inner and middle dentin (Figure 6(c)), the value for tissue closest to the DEJ was significantly greater (p≤0.01) than that located closer to the pulp.

Figure 6.

Relationship between the region of evaluation, and resistance to crack growth. (a) initiation toughness, b) growth toughness, and (c) plateau toughness. In both (a) and (c) the columns with different letters are significantly different (p≤ 0.05).

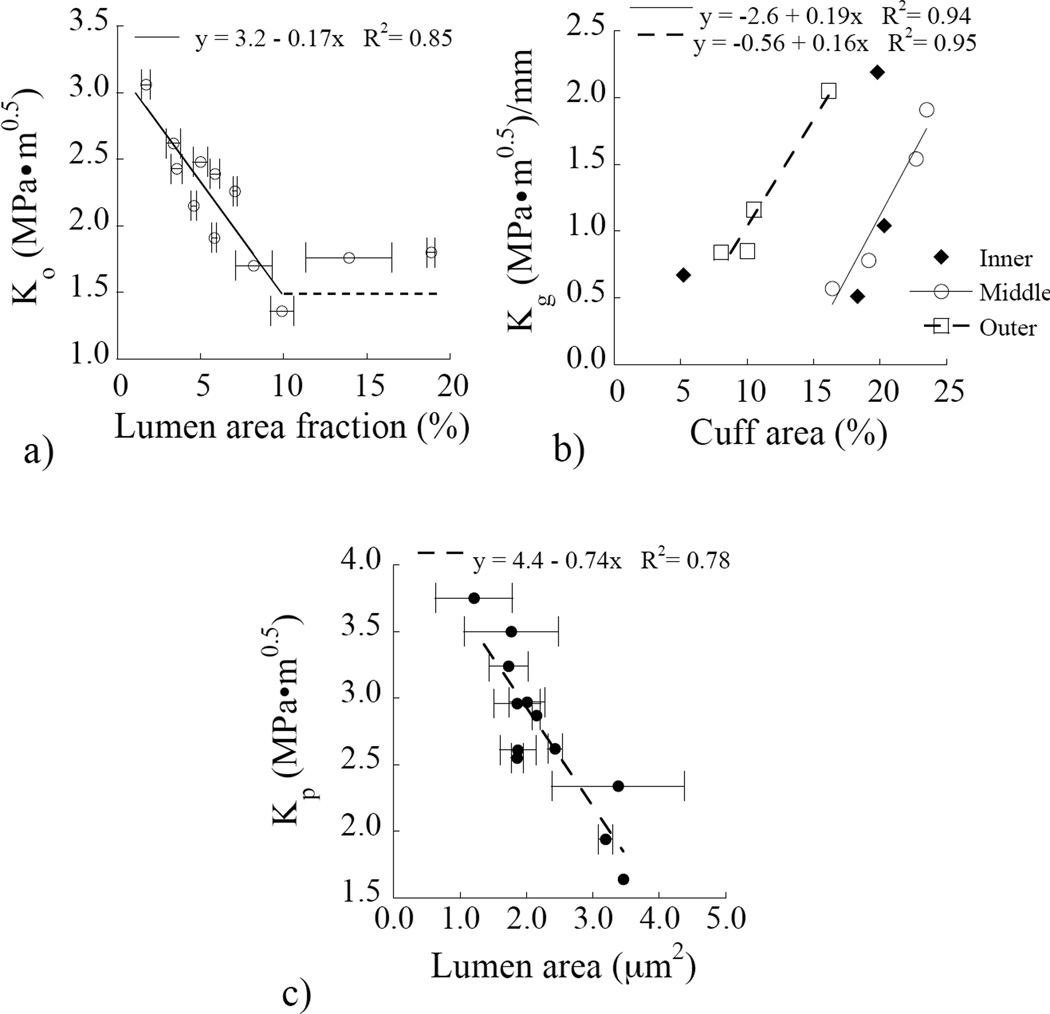
As expected, there were differences in the tubule density, as well as tubule and peritubular cuff geometries in specimens obtained from the three regions. The microscopic analysis revealed that some locations in the specimens were found to exhibit an irregular tubule distribution, an observation reported previously [41], and particularly in the peripheral dentin. As such, the quantitative descriptions for the microstructure were obtained from an average of five measured locations, and excluded any regions of irregular distributions. An evaluation of the crack growth resistance parameters in terms of the microstructure showed that there were some correlations, and only the strongest of those observed are presented. The influence of the area fraction of lumens on the initiation of crack growth is presented in Figure 7(a). Overall, there is a decrease in the K_o as the area occupied by the lumens increases. However, there is a plateau of approximately 1.5 MPa•m⁰⁵ at which the area fracture of lumens occupies over 7% of the total area (Figure 7(a)). Though lumen area fraction was important to the other fracture parameters as well, a stronger correlation was found with other microstructural parameters. As shown in Figure 7(b), there was a marked increase in K_g with percentage area occupied by the cuff in both the middle and outer dentin. Yet, there was no correlation between the cuff area and K_g for inner dentin. For the plateau toughness, the strongest correlation was found with the size of the lumen and lumen area. The maximum crack growth resistance decreased with increasing lumen area as shown in Figure 7(c).

Figure 7.

Relationship between the microstructure and resistance to crack growth.(a) the initiation toughness as a function of the percentage area of the fracture surface occupied by lumens. (b) the growth toughness presented in terms of the percentage fracture area occupied by the peritubular cuff. (c) the plateau toughness as a function of the lumen area.

Micrographs obtained from an SEM analysis of the crack growth process in specimens from the three regions are shown in Figure 8. An examination of the crack path further conveyed that crack propagation in dentin is strongly influenced by the microstructure. In particular, the lumen density and their geometry were found to play important roles in how the crack advanced. For instance, cracks within the inner dentin propagated in the direction of the maximum opening stress, but with preference for the nearest lumen adjacent to the crack tip as shown in Figure 8(a). In addition, some degree of microcracking was observed in the region anterior to the crack tip (approx. 25µm from crack tip) as evident in the figure. Posterior to the crack tip, ligaments of tissue were observed bridging the crack in inner dentin as shown in Figure 8(b).

Figure 8.

Scanning electron micrographs illustrating the toughening mechanisms during crack growth in human coronal dentin. (a) crack extension in inner dentin. The crack primarily extends from lumen to lumen as shown with the white arrows. Some degree of peritubular microcraking is also observed at the crack tip as outlined (white encircled area). (b) Micrograph showing the presence of ligaments bridging the crack in inner dentin (arrows). Notice that the majority of bridging involves bundles of tubules as evident at this lower magnification. (c) Microcracking of 2 the peritubular cuffs is prevalent in central dentin as shown in the highlighted region of the crack wake; (d) example of ligaments bridging the crack and microcracks observed during crack growth in outer dentin.

In mid-coronal dentin the peritubular cuff occupied up to approximately 20% of the total cross-section area, which was much greater than observed in the other regions. Within these specimens microcracking of the peritubular cuffs was a more dominant contributor to the process of crack extension. A typical crack path in mid-coronal dentin is shown in Figure 8(c). About the borders of the crack surface (i.e. in the highlighted crack wake) there is a zone in which the peritubular cuffs have underwent a substantial degree of microcracking. Interestingly, unbroken ligaments of tissue bridging the crack were less frequently observed in this region.

In contrast to the characteristics of mid-coronal dentin the lumens are more distant from one other in outer dentin (Figure 8(d)), and there is a lower area fraction of highly mineralized peritubular cuffs. As a result, the crack is forced to grow within a greater percentage of intertubular dentin within the outer region. Microcracking of the peritubular cuff was noted in the outer dentin, although to a smaller degree than in the middle region, and the development of ligaments behind the crack tip as shown in Figure 8(d); the unbroken ligaments were generally larger than noted in other areas. At higher magnification it was common to observe collagen fibrils spanning the crack faces in areas bordered by intertubular dentin. There was no evidence of debonding between the intertubular and peritubular dentin in any of the three regions evaluated.

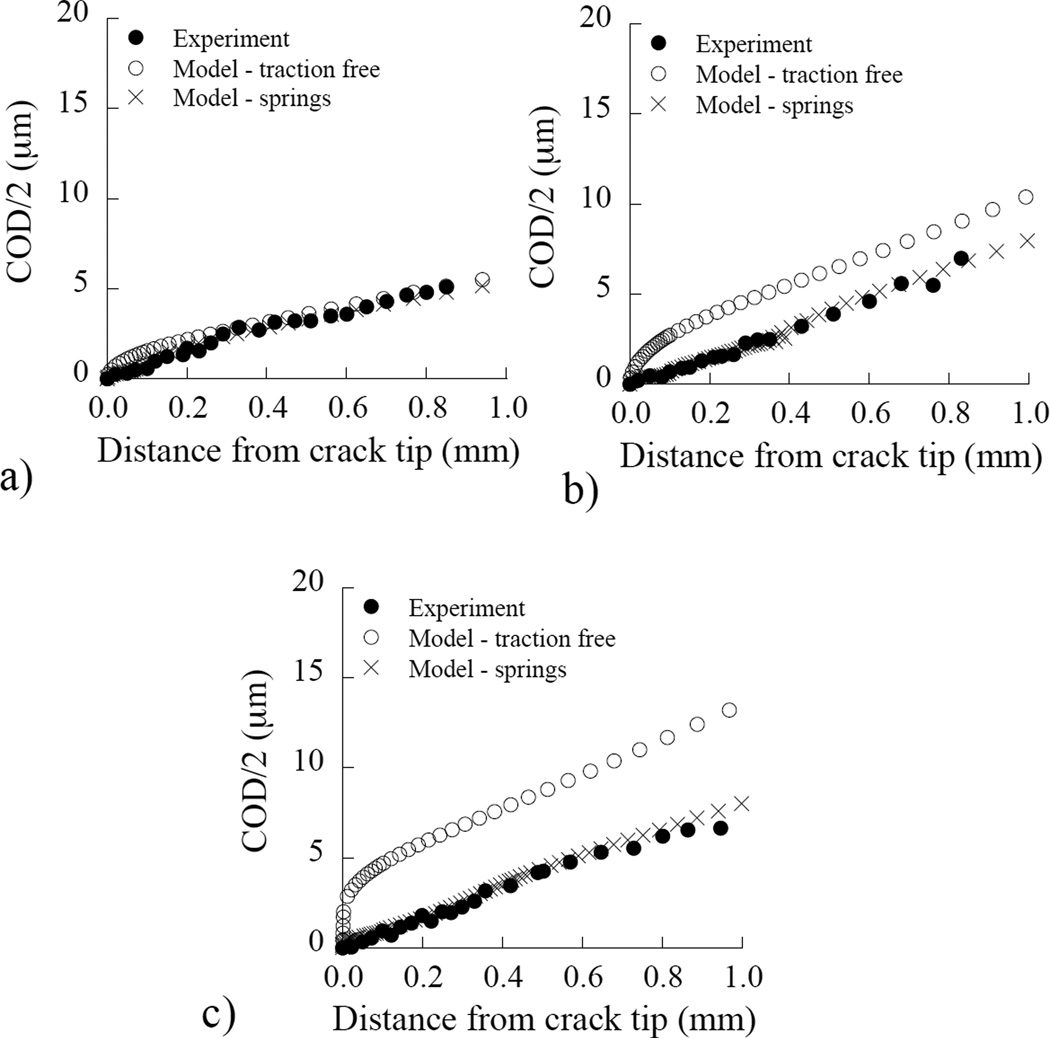
The Crack Opening Displacement (COD) profiles determined from the optical evaluation of the displacement field in representative specimens of inner, middle and outer dentin are shown in Figure 9(a) through 9(c), respectively. These experimental results served as both a basis of comparison and as the solution for a finite element model simulating the crack growth process. Results from the models without the introduction of extrinsic mechanisms of toughening are presented as the “traction” free solution. It is evident that the COD profiles from the numerical model with a traction-free crack surface exhibit greater opening displacement than the profiles obtained from the experiments. The difference between the experimental and the numerical profiles increases as function of distance from the pulp, e.g. the discrepancy between traction free model and experiments increase from Figure 9(a) to 9(c). This difference is attributed to the extrinsic mechanisms acting behind the crack tip in the experiments, which impose traction on the near-tip region. Through the introduction of simulated bridging forces induced by the nonlinear springs (Figure 3), it was possible to achieve agreement in the COD profiles between the model and experiments within 5% error.

Figure 9.

Comparison of the crack opening displacement from the symmetry plane (COD/2) as a function of distance from the crack tip for the experiments and the numerical model. These are representative distributions for (a) inner, (b) middle and, (c) outer dentin. Table 1 Finite element results for the components of fracture energy and toughness for inner, middle and outer dentin.

Estimates for the energy release rate (i.e. J-integral) obtained from the final element model for each region, with and without cohesive zones, are listed in Table 1. The corresponding estimates for the fracture toughness determined according to Eqn. (4) are also presented. Listed in the table are the fracture energy estimated for linear elastic behavior only (J_el), the additional energy associated with the introduction of elastic-plastic constitutive behavior for dentin (J_tip), and the energy stored in the spring elements (J_brid) simulating the bridging stresses that are required to achieve agreement in the experimental and numerical COD profiles. The total fracture energy (J_total) is simply the sum of the three aforementioned components. Based on these mechanisms, toughening promoted by the inelastic deformation (J_tip) contributed roughly 3% to the total fracture energy, whereas extrinsic toughening contributed approximately 26% of J_total. The fracture toughness estimated using EPFM and accounting for the toughening mechanisms (K_eff) is 18% higher than that estimated based on linear elastic fracture mechanics (K_c). Of substantial importance, the contribution of extrinsic toughening is 2.5 times greater within outer dentin than in the inner dentin.

Table 1.

Finite element results for the components of fracture energy and toughness for inner, middle and outer dentin.

Parameter	Region of Evaluation
	Inner	Middle	Outer
JelI	205	355	549
JtipII	2.4	9.2	21.2
JbridIII	77	128	192
JtotalIV	285	492	762
KcI	2.1	2.7	3.4
KeffIV	2.4	3.2	4.0

Units for J and K are Pa•m and MPa•m^1/2, respectively.

^IJ_el is the fracture energy estimated for linear elastic behavior and it is use to calculate K_c

^IIJ_tip accounts for the energy spent in plastic deformation

^IIIJ_brid is the energy stored in the spring elements

^IVJ_total is the total fracture energy and it is use to calculate K_eff

DISCUSSION

An understanding of variations in the fracture toughness of dentin within human teeth is important to the success of restorative dentistry. Fracture, along with recurrent caries and marginal deterioration, are the three primary forms of restored tooth failure [42]. The present study characterized the spatial variations in crack growth resistance of dentin from the crown of unrestored human teeth for the first time and identified relationships between the microstructure and fracture toughness. Results from the experiments showed that is a significant increase in the fracture toughness progressing outward from the pulp to the DEJ. In a previous study, Rasmussen et al [19] reported that dentin is more resistant to fracture near the DEJ than in deeper dentin, based on trends in the work to fracture (W_f). Although results of the present study support that finding, W_f is not a measure of fracture toughness and involves a fundamentally different form of failure. Of additional importance, results from the present study showed that coronal dentin exhibits an increase in toughness with crack extension as noted in previous investigations on human dentin [24, 25, 32]. The significance of findings from this investigation is that crack growth toughening was observed throughout the crown, i.e. in all three regions of evaluation, but specific characteristics of crack growth and the toughening process were site-specific.

An earlier study examined the influence of patient age on the crack growth resistance of human dentin for cracks extending in-plane with the dentinal tubules, which is equivalent to the present orientation. Reported values for the initiation and growth toughness of young dentin in that study were 1 MPa•m^0.5 and 9 MPa•m^0.5/mm, respectively [25]; the apparent fracture toughness of this age group ranged from 1.6 to 2.6 MPa•m^0.5. Although the values of K_o and K_g are not in direct agreement with those determined here, the reported range in fracture toughness is very consistent with the present results (Figure 5(c)), especially for the inner and middle regions. The largest difference is in the growth toughness as the values in Figure 6(b) are less than one third the average reported in Koester et al. [25]. One factor contributing to the differences is specimen geometry. While the initiation toughness is not dependent on specimen type [43], crack growth toughening is generally greater in the bending configuration due to differences in the bridging stress intensity factor [44]. There is also a disparity is the location where the specimens were obtained as those in Koester et al. [25] were obtained from coronal and radicular dentin. There are differences in microstructure between dentin of the crown and root, namely the later has lower lumen density and smaller peritubular cuff thickness than dentin from the crown [45–47]. Both of these features are more akin with those of outer coronal dentin, and would be expected to result in greater toughening. While a comparison of the fracture resistance of radicular and coronal dentin has not been reported for human teeth, there is precedence that toughening in radicular dentin is more potent [48, 49]. Moreover, the diameter of the radicular collagen fibrils is larger [50] and they have a different primary orientation than in the crown [51], both of which would result in greater toughening in radicular dentin. Lastly, it is important to consider that the total crack extension achieved in the study of Koester et al. [25] was less than 250 µm, whereas in the present study the cracks were extended to lengths exceeding 1 mm. As such, the mechanisms represented in toughening are operating at different scales in the two studies and their contributions are averaged over a greater degree of extension in the present investigation.

According to the image analysis the average tubule density of the specimens in the inner, middle and outer groups were 48,500±9,800, 29,200±2,800 and 19,700±3,700 tubules/mm^2, respectively. Consequently, the significant differences in toughening behavior between locations (Figure 6) were an indirect reflection of the importance of tubule density. Overall, the increase in fracture toughness from the inner to the outermost dentin is significant, and the K_c values obtained for the outer region (Figure 6(c)) are amongst the largest reported for coronal dentin in the literature. But it is important to put the spatial variations in toughness in perspective with the effects of tubule orientation. Nazari et al [24] evaluated the fracture toughness of dentin for cracks extending perpendicular to the lumens, i.e. the 90° degree orientation. The average fracture toughness in this orientation (1.65 MPa*m^0.5) is approximately 60% lower than the average value for the 0° orientation (2.72 MPa*m^0.5) considering all three regions. For cracks extending in-plane with the tubules, the opening direction is aligned with the collagen fibers primary direction [2], increasing the potency of posterior crack-bridging forces caused by collagen fibrils and unbroken ligaments of tissue. Also, when comparing the R-curves for the two orientations, the extrinsic mechanisms for the 0° orientation are active over a larger crack extension (Δa≤0.5mm) than those mechanisms present in the 90° orientation (Δa≤0.35mm). If the degree of anisotropy in fracture resistance is defined according to K_c(0°)/K_c(90°), using results from the present study and Nazari et al., [24] provides a ratio of approximately 1.6, which is comparable with other studies [22, 23]. The ratio in fracture toughness between the outer (3.39 MPa*m^0.5) and inner (2.07 MPa*m^0.5) dentin is approximately 1.7. Thus, the magnitude of spatial variations in fracture toughness is equivalent or greater than the degree of anisotropy. These results further substantiate the assertion that restorations extended into deep dentin are far more likely to facilitate tooth fracture [13], and the primary cause is the gradient in crack growth resistance with depth.

Evaluations of the crack path and fracture surfaces using electron microscopy provided further insight on the importance of microstructure to the mechanisms of crack extension. A combination of toughening mechanisms contributed to the mechanics of crack growth. There was evidence of crack bridging by unbroken ligaments of tissue, crack branching, crack deflection and microcracking. But the relative frequency of occurrence and their contributions to the overall crack growth resistance was dependent on location and the specimen microstructure. Nalla et al [22] commented that the tubules do not play a direct role affecting the fracture toughness of dentin. Of relevance here, that study was performed on elephant dentin (i.e. elephant tusk ivory), which possesses smaller lumen diameters and peritubular cuff thickness, as well as a lower number of lumens in comparison to human coronal dentin. Based on our observations of crack growth in human dentin, that statement is perhaps applicable for the outer region where the majority of the fracture area is occupied by intertubular dentin. But it does not apply to the other two regions. The lumen diameter was found to be of primary importance to the initiation toughness (Figure 7(a)). Within inner dentin the lumens are highly influential to the crack path (Figure 8(a)), and the increment of energy needed to achieve growth. Toughening was achieved by meandering of the crack to adjacent lumens, and the development of unbroken ligaments. Within the specimens of middle dentin, microcracking of the peritubular cuff was most prevalent, and indeed the cuff area was noted as one of the most important microstructural parameters to the growth toughness in this region (Figure 7(b)). Microcracking spurred the development of satellite cracks, which then eventually linked with the main crack but facilitated the development of unbroken ligaments causing crack closure stresses. Crack growth within outer dentin was accompanied by extensive posterior bridging by unbroken ligaments, which rendered the largest extrinsic component of crack growth toughening (Table 1). The lumen size was identified to be the most important microstructural parameter to the plateau toughness (Figure 7(c)), which is expected to originate from their influence to the ligament size that developed via the mechanisms of crack growth.

Though there are substantial changes in the microstructure with increasing distance from the DEJ and a corresponding reduction in the fracture toughness, all three regions evaluated were found to exhibit rising R-curve behavior. The toughening occurred by the development of unbroken ligaments of tissue, collagen fibril bridging and microcracking (Figure 8). But which mechanism was most potent? Previous studies [30, 31] have estimated the contributions from extrinsic and intrinsic toughening to the crack growth resistance of dentin. In these investigations classic analytical models were adopted to account for microcracking [52–54], collagen fiber bridging [55] and uncracked ligament bridging [56]. In general, these models rely on a combination of experimental observations and supporting assumptions, and as such are limited to the strength of the assumptions. If this discussion on fracture mechanisms is extended to bone, there have been evaluations of the crack growth resistance performed via numerical analysis with cohesive elements [57] and non-linear process zone models [58]. But in these models the contributions from intrinsic and extrinsic toughening are generally not viewed independently, making it impossible to differentiate the two. The hybrid approach, involving a numerical model driven by experimental results, enabled a determination of the individual contributions from unbroken ligament bridging and inelastic deformation for the first time. Results for the energy to fracture showed that the extrinsic mechanisms (consisting of bridging forces posed by fibrils and unbroken ligaments) accounted for 26% of the total energy required for fracture in all three regions (Table 1). This estimate is in close agreement with the estimates from Kruzic et al [32], which were obtained using analytical models based on first principles. Accounting for near crack tip plasticity indicated that it represented only 3% average increase in the energy to fracture in all three regions. Thus, dentin is primarily an extrinsically toughened tissue and the majority of toughening rise in crack growth resistance with crack extension is attributed to the strength of the bridging elements. Even though crack growth within inner dentin is accompanied by the formation of ligaments, they are intrinsically weaker [8, 9, 12] and impose a lower degree of crack closure stress that consumes fracture energy.

In an earlier study concerned with toughening in human dentin [33], the fracture toughness for crack growth parallel to the longitudinal axes of the tubules was estimated using EPFM. It was found that the effective fracture toughness (3.1±0.3MPa*m^1/2) was 29% greater than that based on LEFM (2.4±0.2 MPa*m^1/2). That is substantially greater than the 17% average difference in estimated toughness in the present investigation between the estimates obtained from LEFM and EPFM (Table 1). However, in Yan et al [33] all of the nonlinearity in fracture behavior was attributed to inelastic deformation and there was no separation of the intrinsic and extrinsic mechanisms. There are other differences as well, including the orientation of crack growth and the mode of loading, as the earlier study was performed in bending using a central edge notch, which involves the earlier concern of differences in specimen type and toughening. Clearly the aforementioned study provided fundamental information regarding the fracture properties of dentin. And indeed, accounting for the contributions of inelastic deformation is important in a rigorous estimation of the fracture toughness of dentin. However, our findings showed that toughening in human dentin is mostly provided by the unbroken ligaments bridging the crack, which promote crack closure and a reduction in stress intensity at the crack tip. That mode of toughening is greatest in the outer dentin and in tissue closest to the DEJ. While there are changes in the characteristics of crack extension with depth that cause a graded fracture toughness, extrinsic toughening plays the largest role in toughening throughout the crown.

The present study combined experimental and numerical components of evaluation to provide a detailed understanding of the fracture behavior of human coronal dentin. As there is presently no clinical approach for arresting cracks in teeth, decreasing the likelihood of their initiation and potential for growth are arguably the best practices for preventing tooth fracture. Results of the experiments distinguished that deep dentin exhibits a significantly lower crack growth resistance than the tissue closer to the DEJ, which further supports conservation of tissue and limiting the depth of excavations. The findings also convey that there is a reduction in the “damage tolerance” of coronal dentin with increasing depth. That raises the importance of using a finishing process to minimize the size of flaws introduced while cutting the preparation [14], and in the potential for identifying methods of healing residual defects.

As with all investigations, there are limitations to the present evaluation that should be considered in their impact on clinical practice. Two of the most important limitations concern the selection of teeth. This investigation focused on the spatial variations in young coronal dentin. There is a significant reduction in the fracture toughness of dentin with aging [24, 25], and there are changes in the mechanisms of toughening and their potency. Furthermore, sclerosis begins in the root and progresses in the crown [e.g. 59, 60], suggesting that the noted spatial variations in crack growth resistance may not represent those in the teeth of seniors, nor reflect the changes in radicular dentin. These concerns are the focus of our future studies.

CONCLUSIONS

On the basis of the results obtained, the following conclusions may be drawn:

1. The initiation toughness (K_o) of outer dentin (2.65±0.3) was significantly greater than that of tissue located closest to the pulp (1.66±0.2). Furthermore, the fracture toughness (K_c) of outer dentin (3.36±0.3 MPa•m^0.5) was also significantly greater than that of the inner dentin (2.22±0.5 MPa•m^0.5). There was no significant difference found between the growth toughness in the three regions evaluated.

2. The K_o and K_c were most strongly influenced by the tubule dimensions. Both of these components of toughness decreased with increasing tubule lumens. The growth toughness (K_g) exhibited the largest correlation with the peritubular cuff thickness, showing an increase in unit toughening with increasing cuff area fraction.

3. Toughening was achieved by the mechanisms of crack advance. Within inner dentin crack growth proceeded along the path of closest adjacent lumens. Microcracking of the peritubular cuffs was observed in middle dentin and the crack advanced through the development of secondary cracks at these fractured cuffs. The distance between lumens was integral to the development and size of unbroken ligaments of tissue bridging the crack. In outer dentin, unbroken ligaments of tissue developed from secondary cracks adjacent to the crack path, not necessarily from microcracking of lumens. These unbroken ligaments caused crack bridging and a reduction in the local stress intensity.

4. The intrinsic and extrinsic mechanisms of toughening contributed an average of 3% and 26% of the total energy to fracture. Thus, coronal dentin is primarily extrinsically toughened. The degree of extrinsic toughening in outer dentin was 2.5 times greater than that in inner dentin. The spatial variations are believed to result from the higher relative collagen content in outer dentin, which increases crack closure stresses caused by the unbroken ligaments and fibrils.