Figure 1.

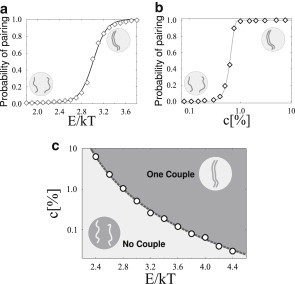
Colocalization in a system with two polymers. The equilibrium colocalization probability, p, of the polymers is shown (a) as function of the bridging molecule binding energy, E (at a fixed value of molecule concentration c = 1.0%) in Model A (Model B gives similar results). p(E) has a sigmoidal behavior highlighting that stable colocalization is only possible if E rises above a threshold value (defined, conventionally, by the inflection point of the curve). (b) p is plotted as function of the concentration, c, of bridging molecules for a fixed value of E (here E = 2.8 kT), showing a similar threshold behavior. In our models, polymer colocalization results from a thermodynamic phase transition occurring in the system. (c) Phase diagram in the (c,E) plane. (Circles) Values of (c,E) at which the phase transition takes place. For (c,E), below the indicator (dashed line), the two polymers diffuse independently, while above threshold they stably colocalize at equilibrium, kept together by the bridging molecules.