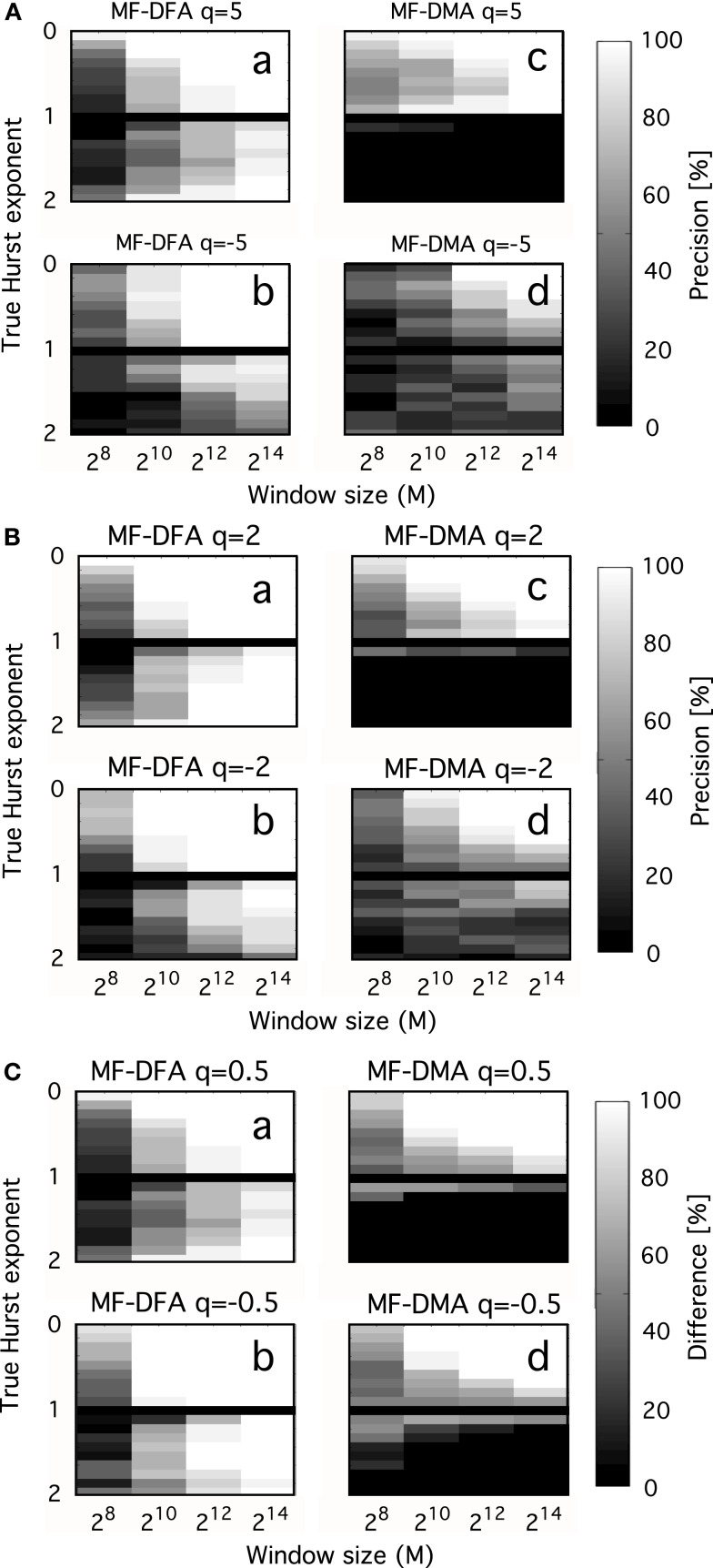
Figure 6.

Precision as a function of moment order, signal length, and Hurst exponent. Precision of MF-DFA [left side of (A–C)] and MF-DMA [right side of (A–C)] as a function of q, H_true, N. fGn and fBm signals were generated by DHM with length of 2⁸, 2¹⁰, 2¹², 2¹⁴, and H_true increased from 0.1 to 1.9 in steps of 0.1, skipping H_true = 1 (corresponding to 1/f boundary seen as the black horizontal line in the middle). Estimation of the generalized Hurst exponent should not depend on q, as monofractal’s H(q) is a theoretically constant function scattering around H_true across different order of moments. The intensity-coded precision index is proportional to the number of estimates of H falling into the range of H_true ± 0.1, with lighter areas indicating more precise estimation. Calculation of this measure is based on 20 realizations for each q, H_true, N. (A) Performance of methods for q = ± 5. (B) Performance of methods for q = ± 2. (C) Performance of methods for q = ± 0.5. Besides the clear dependence of precision on H_true and N, influence of moment order is also evident, given that the lightest areas corresponding to the most reliable estimates tend to increase in parallel with moment order approaching 0 [Note the trend from (A–C)]. The lower half of the plots indicates that MF-DFA is applicable for signals of both types, while MF-DMA is reliable only on fGn signals. This result is further supported by the paper of Gao et al. (2006), who demonstrated a saturation of DMA at 1 for H when the true extended Hurst exponent exceeds 1 (thus it is non-stationary)