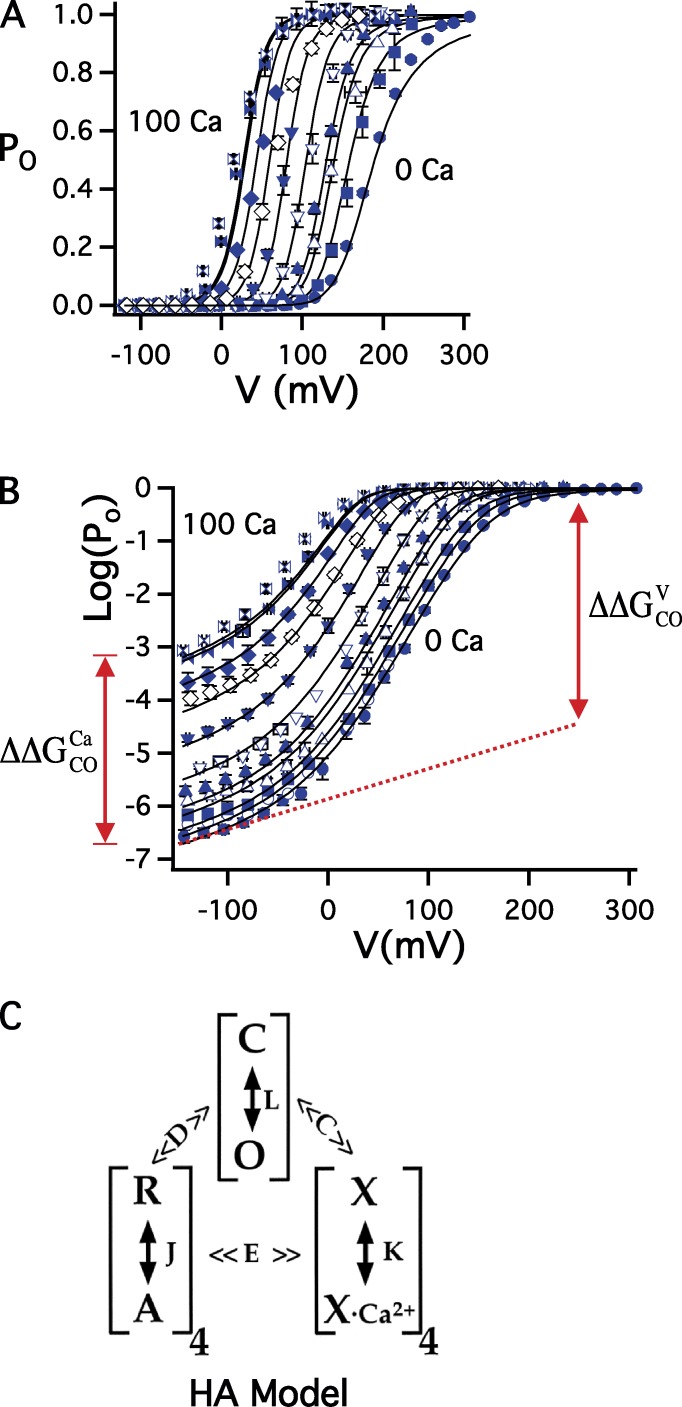
Figure 2.

Voltage- and Ca²⁺-gating of BK channels. (A) P_O-V relations for mSlo1 estimated as G_K/G_Kmax from macroscopic tail currents after 30 ms voltage pulses in 0–100 µM Ca²⁺. (B) Log(P_o)-V relations extend P_O to <10⁻² using steady-state unitary current recordings from macropatches. A and B represent mean ± SEM and are fit (solid curves) by the HA model (Horrigan and Aldrich, 2002). The increase in Log(P_o) from 0 Ca²⁺ to saturating 100 µM Ca²⁺ at −120 mV (where voltage-sensors are in the resting state) reflects Ca²⁺-sensor/gate coupling energy ($\Delta \Delta {\mathrm{G}}_{\text{CO}}^{\text{Ca}}$). The increase in Log(P_o) in 0 Ca²⁺ from −120 mV to ∼+300 mV (where voltage sensors are fully activated) reflects voltage-sensor/gate coupling ($\Delta \Delta {\mathrm{G}}_{\text{CO}}^{\mathrm{V}}$). The values of $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{Ca}}$ and $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{V}}$ are determined from the change in the free energy of the gate (e.g., $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{Ca}}=\Delta {\text{G}}_{\text{CO}}\left[100\hspace{0.17em}\text{Ca}\right]-\Delta {\text{G}}_{\text{CO}}\left[0\hspace{0.17em}\text{Ca}\right]$, where $\Delta {\text{G}}_{\text{CO}}=\mathit{kT}\text{ln}\left[{\text{P}}_{\text{O}}/\left(1-{\text{P}}_{\text{O}}\right)\right]$), and, in the case of $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{V}}$, the measurement at −120 mV must be extrapolated to positive voltages (dashed line) to correct for the weak voltage dependence of the C-O transition (z_L = 0.3 e). (C) Allosteric model indicates the possible conformations of the gate (C and O), voltage sensors (R and A), and Ca²⁺ sensors (X and X-Ca²⁺) in each of four subunits and allosteric factors (C, D, and E) that describe the energetic coupling between these three parts of the channel. J and L are voltage-dependent equilibrium constants with zero-voltage values J₀ and L₀ and partial charges (z_J, z_L), K = [Ca²⁺]/K_D, where K_D is the elementary Ca²⁺ dissociation constant for the closed channel.